注塑机炮筒内注射压力损失研究

0 引 言

注射成型工艺参数设定是强经验、弱理论的领域，其精确的数学模型难以建立

，而数据分析技术是从历史数据中发现知识的方法，不需要复杂的理论构建，因此被越来越广泛地应用到该领域中。如张玲利等

利用多元回归分析建立了注射压力和模具温度与成型制品几何尺寸之间关系的回归模型；谢北萍等

通过研究不同部位的型腔压力曲线，探讨了制品残余应力和型腔压力曲线之间的关系；SHEN C Y等

结合神经网络和遗传算法优化注射工艺参数，降低了成型制品的体积收缩；刁思勉等

通过建立原材料、模具温度与制品成型质量之间的神经网络模型，提出一种注射过程监测方法，实现故障监测和质量预测。

在以往的生产实践中，工程人员只能获取注塑机炮筒内的注射压力数据，因此常将炮筒内的注射压力等效为模具型腔内注射压力而忽略了炮筒内的注射压力损失。随着注射成型技术的发展，越来越多的从业者意识到影响注射成型制品质量的关键指标是模具型腔内注射压力而非注塑机反馈的炮筒内注射压力，开始重视对注塑机炮筒内注射压力损失的研究，但较少有系统性的研究数据和结论见诸报道。

根据塑料注射成型领域的技术发展趋势，结合行业现状，现开展注塑机炮筒内的注射压力损失研究，通过一系列试验获取数据，并利用数据分析技术发掘炮筒内的注射压力损失模式，提高了注塑机炮筒内注射压力损失的预测精度。

1 用于研究的设备与模具

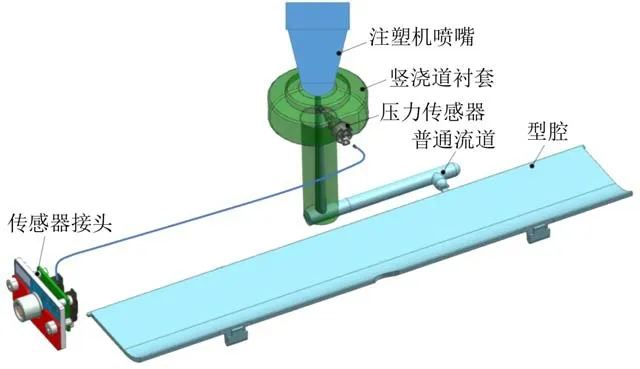
注射成型试验在1 200 kN 的电动注塑机上进行，该注塑机采用全电机驱动以及PLC、变频和伺服控制技术，能实现高精密控制。注塑机稳定的控制性能可以确保试验结果的可靠性和稳定性。用于研究的模具是1副浇口处安装有压力传感器的普通流道的两板模，型腔尺寸为301 mm×57 mm×2.5 mm，成型的制品厚度均匀、结构简单，可以实现低成本高效率的注射试验过程。

如果pts1,pts2,,ptsc为一组最底层并行工序任务串，其中任一并行工序任务串ptsb(1≤b≤c)可表示为ptsb={pthi,pth(i+1),,pthu}，pthi,pth(i+1),,pthu为ptsb中包含的工序任务，则ptsb的工时

通过求ΔP

与P

数据集的R

=0.981，ΔP

与V数据集的R

=0.282，ΔP

与T 数据集的R

=0.534，确定炮筒内注射压力损失ΔP

与炮筒内注射压力P

的相关程度最高，再通过最小化误差的平方和寻找数据最佳函数匹配的数学优化技术

（最小二乘法），拟合ΔP

与P

数据集的最佳匹配函数，得到ΔP

关于P

表达式：

2 测试试验

2.1 试验方法

通过以上方法整理各组试验数据，构建试验数据表，6种材料共进行132组注射试验，受限于篇幅，表2仅列出部分试验数据。

2.2 试验数据收集

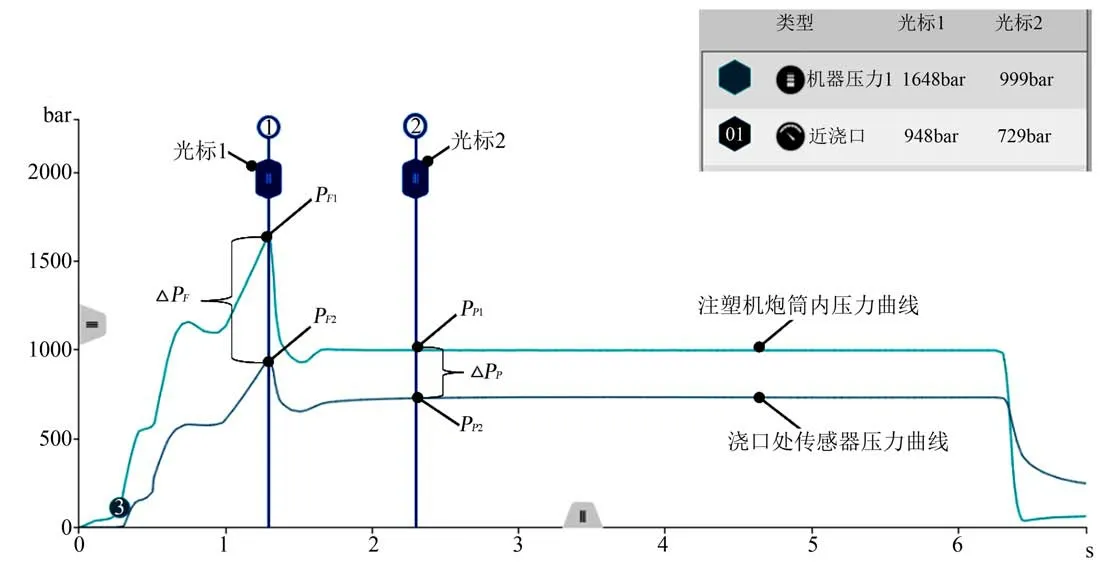
通过一系列的注射成型试验，获得各种材料不同工艺条件下的注塑机炮筒注射压力和模具传感器压力曲线，取注塑机炮筒注射压力曲线V/P 切换时刻的压力值P

与模具传感器压力曲线V/P 切换时刻的压力值P

求差得到ΔP

，表征填充阶段注塑机炮筒内的注射压力损失。如图2 所示，填充阶段注塑机炮筒内的注射压力损失ΔP

=1 649-946=703 bar。

两组患者均进行糖化血红蛋白检测、空腹血糖水平以及口服葡萄糖50 g筛选测试糖耐受量水平：采用专业生化负压采血管，于清晨抽取患者3 mL空腹静脉血；随后给予患者口服50 g葡萄糖，服用1 h后抽取患者3 mL静脉全血并进行血清分离。

3 试验数据分析

3.1 试验数据整理

由于研究试验旨在探索影响注射过程中炮筒内注射压力损失的因素，选择与压力相关程度较高的注射速度、熔体温度以及材料类型3 个对象作为研究变量，用单点参考黏度指数（VI）介于51.6～327.2 的6 种材料（单点参考黏度指数是在指定的温度和剪切速率为1 000/s）的条件下，使用Cross-WLF黏度模型计算的黏度可在一定程度反应材料的流动性，分别以20～180 mm/s 的螺杆速度，在不同的熔体温度条件下执行注射试验，采集各种注射试验下的注塑机炮筒内注射压力和模具传感器压力，研究试验材料清单如表1所示。

3.2 试验数据线性回归分析

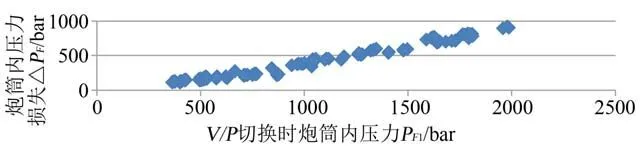
根据试验数据，分别绘制ΔP

与P

、ΔP

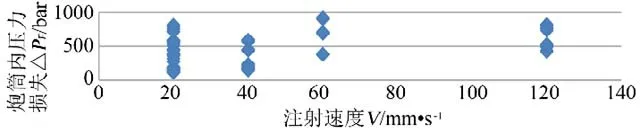
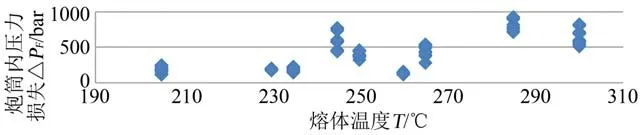
与注射速度V、ΔP

与熔体温度T 的散点图，如图3～图5所示。

自然科学领域中皮尔逊相关系数广泛用于度量2 个变量之间的相关程度，其值介于-1～1。皮尔逊相关系数通常用字母R 表示，其值为负说明变量之间负相关，为正则说明正相关，且R 的绝对值越大，2 组数据的相关程度越高。因此可以分别计算ΔP

与P

、V、T以及3组数据的皮尔逊相关系数并开方，用于度量ΔP

与3个变量之间相关程度的指标。

从表1可得国内正念疗法研究领域前22个热点，较为集中的前10个热点分别为：正念(54)、正念训练(48)、心理健康(35)、社会生活问题(14)、躯体疾病(13)、MBSR(12)、正念干预(11)、主观幸福感(8)、冥想(7)、运动员(7)。透过高频词可摸清正念领域研究之表象，但难以挖掘关键词间的关系。故而，进行关键词共现技术进一步发掘它们彼此间的内在构架。

散点图是确定2 个数值变量之间是否存在联系、模式或趋势最有效的图形方法之一

。因此，比较图3～图5 的散点分布可以发现：ΔP

与P

之间存在很强的相关性（标绘点的模式从左下到右上倾斜，意味着P

值随ΔP

值的增加而增加，暗示正相关

），而注射速度V和熔体温度T几乎不相关。

为了方便数据采集和分析，利用ComoDataCenter（注射过程数据中央存储系统），集中采集和处理注塑机炮筒内注射压力与模具浇口处传感器压力数据，注射试验模型如图1所示。

对于保压阶段炮筒内注射压力损失的计算，则取V/P 切换后浇口处传感器压力达到最大值时刻，注塑机炮筒内压力曲线的压力值P

和浇口处传感器压力曲线的压力值P

之差ΔP

即为保压阶段炮筒内注射压力损失，保压阶段注塑机炮筒内的注射压力损失ΔP

=999-732=267 bar。

本经济型直筒结构的建筑木模板组件在大型混凝土浇筑件或者小型混凝土浇筑件浇筑时均可以使用，并且混凝土浇筑件的浇筑效果好。同时，紧固组件的结构简单，拆装方便，其中环形紧箍选用钢筋，由于钢筋是柔性的，可以沿胶合面板的曲面弯曲并且在施工后也方便进行矫直已备作下次使用，经济效益佳。本技术所提供的建筑木模板组件还具备了施工快速高效，材料损耗小，节约成本等优点。

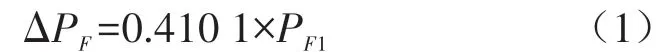
式（1）可以作为填充阶段注塑机炮筒内注射压力损失的一种预测模型，在实际生产中，注塑机炮筒内的注射压力值容易获得，因而此类模型具有广泛的适用性。

1.3 统计学处理 采用SPSS 19.0统计软件进行数据处理与分析，双人双录，以P<0.05为差异有统计学意义。

同理，根据研究试验数据，绘制保压阶段炮筒内注射压力损失ΔP

与保压阶段炮筒内注射压力P

的散点图，如图6 所示，并拟合保压阶段炮筒内注射压力损失ΔP

与保压阶段炮筒内注射压力P

数据集的最佳匹配函数：

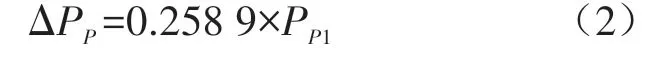
以上研究表明，注塑机炮筒内注射压力损失与注射速度和熔体温度相关性不大，而与炮筒内的注射压力表现为强相关，并且可以通过构建f（x）=kx函数来表达其相关性，其中f（x）为注塑机炮筒内的注射压力损失，x 为注塑机的炮筒注射压力，k 为压力损失系数。此外，式（1）和式（2）揭示了在不同的注射阶段（填充和保压），炮筒内的注射压力损失系数不同的基本现象。

4 结束语

长期以来工程人员对注塑机炮筒内的注射压力损失缺乏研究，流动仿真分析一般只考虑模具内的压力传递，以至于对注射压力的预估出现偏差。现揭示了一种新的注塑机炮筒内注射压力损失模式：ΔP

=k

P

、ΔP

=k

P

；其中，k

k

为填充、保压阶段的压力损失系数。基于回归分析法，对大量统计数据进行数学处理，确定因变量与某些自变量的相关关系，建立相关性较好的回归方程（函数表达式）

，研究构建了注塑机炮筒内注射压力损失的预测模式，可以优化试模过程中的注射压力设置，协助工艺人员快速寻找更合理的注射压力和保压压力。因受限于测试条件，并未对不同注塑机之间的炮筒注射压力损失系数进行研究和分析，尚不明确炮筒内注射压力损失系数与注塑机设备参数之间的关联，随着研究的不断深入，越来越多与炮筒内注射压力损失相关的影响因素会被挖掘，用于完善和提升注塑机炮筒内注射压力损失的预测模型，并推动流动仿真分析软件的压力求解器改进，促进注射工艺优化方法自动化和智能化发展。

[1]周华民,高 煌,张 云,等.注塑成型工艺参数自动设置与优化技术[J].精密成型工程,2016,8(1):7-13,26.

[2]张玲利,吴大鸣,张丽蕾.注塑成型过程中的多元回归分析[J].塑料,2007,36(3):76-79.

[3]谢北萍,刘 斌.采用模腔压力曲线的注塑成型实验[J].华侨大学学报(自然科学版),2014,35(6):611-615.

[4]SHEN C Y,WANG L X, LI Q.Optimization of injection molding process parameters using combination of artificial neural network and genetic algorithm method[J].Journal of Materials Processing Technology,2007,183(2-3):412-418.

[5]刁思勉,乔海玉,贺 鉴,等.基于注塑机螺杆位置与压力曲线的注射成型过程监测方法[J].模具工业,2022,48(2):1-7.

[6]HAN J W.数据挖掘:概念与技术(原书第三版)[M].范明,译.北京:机械工业出版社,2012:36-37.

[7]曹连江.电子信息测量及其误差分析校正的研究[M].长春:东北师范大学出版社,2017:260-261.

[8]盛 骤.概率论与数理统计[M].北京:高等教育出版社,2010:191-192.