基于TAC-Heric的光伏并网逆变器拓扑控制研究

古纯松，陈 众，谢 辉，马希永

(长沙理工大学智能电网运行与控制重点实验室，湖南长沙 410114)

随着我国新能源发电系统的发展，对于光伏发电的需求日益增长，导致光伏发电系统中的并网逆变器市场份额增长迅速[1]。光伏并网逆变器通常分为两种结构[2]：一种是隔离型，其利用变压器实现直流、交流侧的电气隔离，从而避免共模电流的产生，但缺点是体积大、成本高、结构复杂、效率低[3-4]；另一种为非隔离型，体积相对小、质量相对较轻、结构简单、成本低以及效率高等优点[5-6]。但由于无电气隔离，逆变器开关管的高频动作会导致共模电压，其在由寄生电容[7]、逆变器和电网交流侧组成的回路中向光伏发电系统注入漏电流[8]，并造成并网电流畸变、EMI、危及人身安全等各种问题[9-10]。

目前，对于非隔离型光伏并网逆变器的研究，已有诸多学者进行了深入探索。文献[11-12]基于H5、H6 拓扑、Heric以及HB-ZVR 拓扑，分析了其在不同情况下(续流阶段、导通阶段、关闭阶段等)的漏电流抑制情况。文献[13]采用中点箝位法，通过在桥臂中点之间接入有源、无源通路，实现对中点电压的有效箝位，研究分析表明该控制策略可对漏电流进行有效抑制。文献[14]基于一种新型的单相无变压器型并网逆变器拓扑结构，在续流阶段，将共模电压箝位至母线电容中点处，从而实现共模电压的有效抑制，采用该拓扑结构可有效抑制漏电流。值得注意的是，以上文献均没有考虑到对中点箝位型逆变器的控制策略，存在电流谐波畸变率高、系统抗干扰能力弱的问题。

因此，针对非隔离型光伏并网逆变器的漏电流抑制以及控制策略优化的问题，本文首先基于传统Heric 拓扑技术，在其拓扑分压电容中点与续流桥臂中点之间添加T 型通路，以此来对中点电压进行有效箝位，并在单极性SPWM 调制方式下，分析了漏电流的形成机理以及TAC-Heric 拓扑的工作过程，以维持共模电压恒定为控制目标，从而实现漏电流的有效抑制。其次，对TAC-Heric 拓扑的控制策略问题进行优化，对PI、PR 以及QPR 控制器的控制特性进行分析，在此基础上，采用PI+QPR 综合控制策略，有效降低了电流谐波畸变率，提高了系统的电能质量。最后基于Simulink 仿真平台，理论和仿真分析验证了TAC-Heric 能更好地抑制漏电流以及所提控制策略的可行性。

1 传统光伏并网逆变器漏电流产生机理

光伏并网系统的拓扑结构如图1 所示，UPV为光伏并网系统的直流侧电压，C为直流侧电容，CPV为光伏阵列对地电容，Ucm为CPV上产生的共模电压，Icm为漏电流，UAN和UBN表示桥臂中点到直流母线N 点的电压，UL为电感L1、L2上产生的压降，Ug为电网电压，接地阻抗较小,可以忽略不计。

在图1 中，以电网电流正半周期为例，根据KVL 列写回路电压方程：

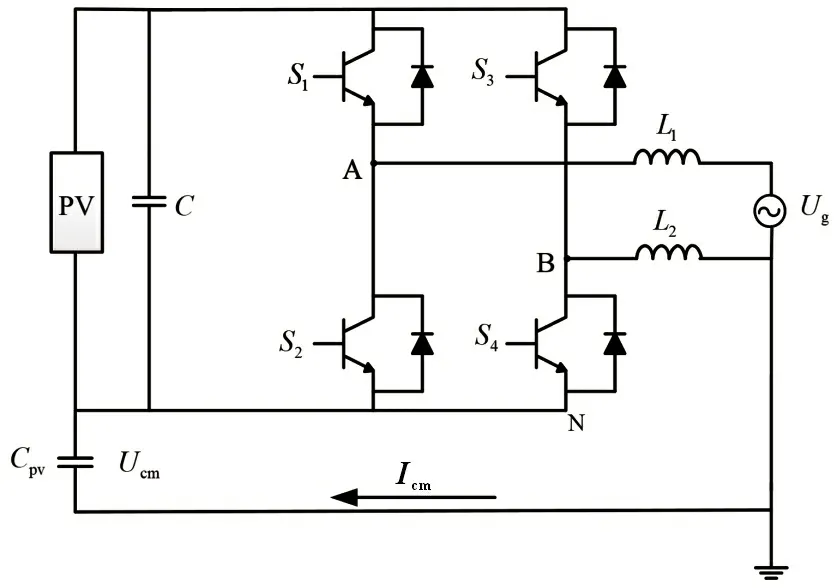
图1 单相无变压器型全桥式拓扑结构

由于漏电流Icm很小，因此可以忽略Icm在L1和L2上的压降，在电感L1、L2参数对称(L1=L2)的情况下，可得UL1=UL2，工频电网电压Ug作用在CPV上产生的漏电流也可忽略不计。根据式(1)和式(2)可得：

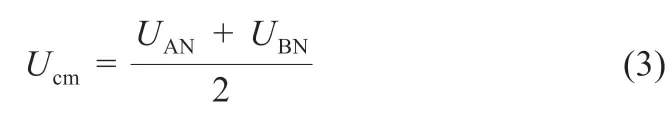
共模电压Ucm和漏电流Icm之间的关系可以表示为：

由式(3)和式(4)可知，要想对漏电流进行有效抑制，就必须维持共模电压Ucm为一恒定数值。

通过采用单极性SPWM 调制，可以实现单相全桥逆变功率开关管的导通与关断，逆变器工作在正半周期时，开关管S1、S4处于导通状态，相应的共模电压为：

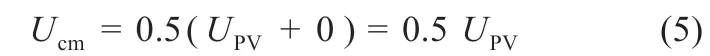
逆变器工作在负半周期时，开关管S2、S3处于导通状态，相应的共模电压为：

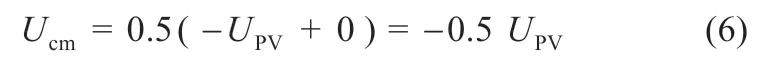
在正半周期续流阶段，电流经S2与S4的反并联二极管导通。在负半周期续流阶段，电流经S1与S3的反并联二极管导通，其共模电压均为：

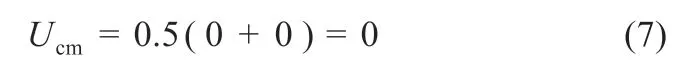
因此，在一个周期内，由式(5)～(7)可知，共模电压在0.5UPV、-0.5UPV和0 之间变化，由式(4)可知系统此时会产生较大的漏电流。

2 新型TAC-Heric拓扑分析

2.1 新型TAC-Heric 拓扑的工作原理及漏电流分析

Heric 拓扑在实际运行中，无法保证交流桥臂中点电压的稳定性，使得其共模电压呈现悬浮状态。为了解决中点电压悬浮问题，本文在Heric 拓扑的基础上进行了相应改进，即在Heric 拓扑的分压电容C1与C2的中点和续流桥臂中点之间引入一条T 型通路，如图2 所示，其中交流桥臂的中点设为N，分容电压的中点设为M。

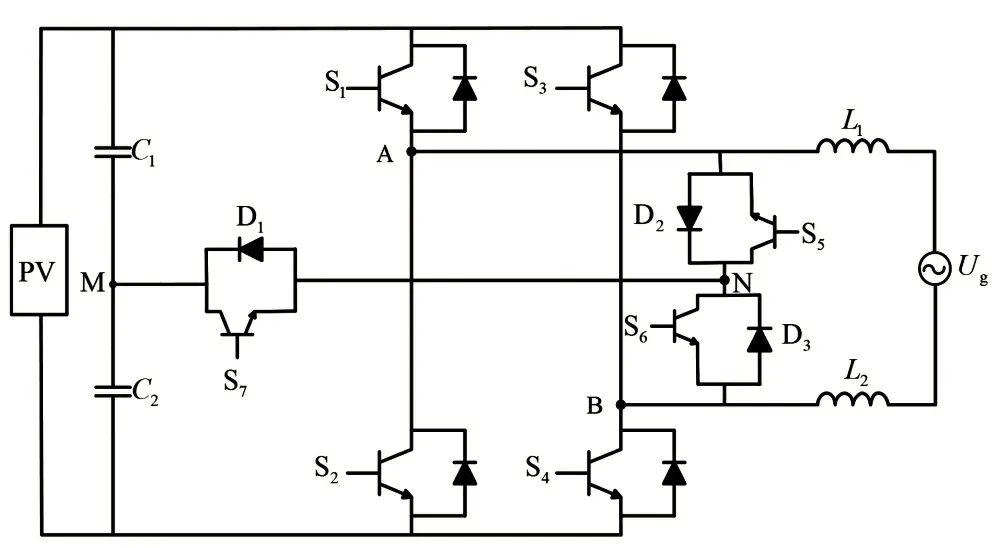
图2 新型TAC-Heric拓扑

为进一步分析本文所提出TAC-Heric 控制具备更加优秀的箝位性能，以正半周期为例，其工作过程如图3 与图4 所示。

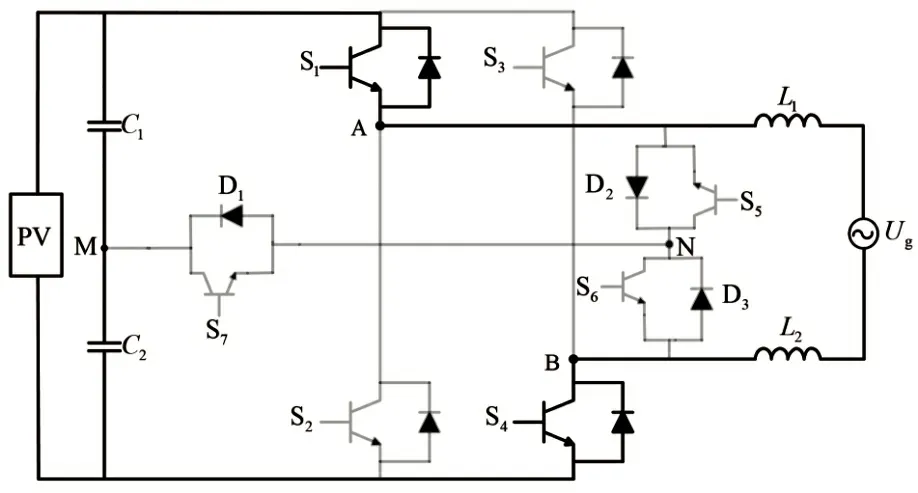
图3 正半周期工作原理

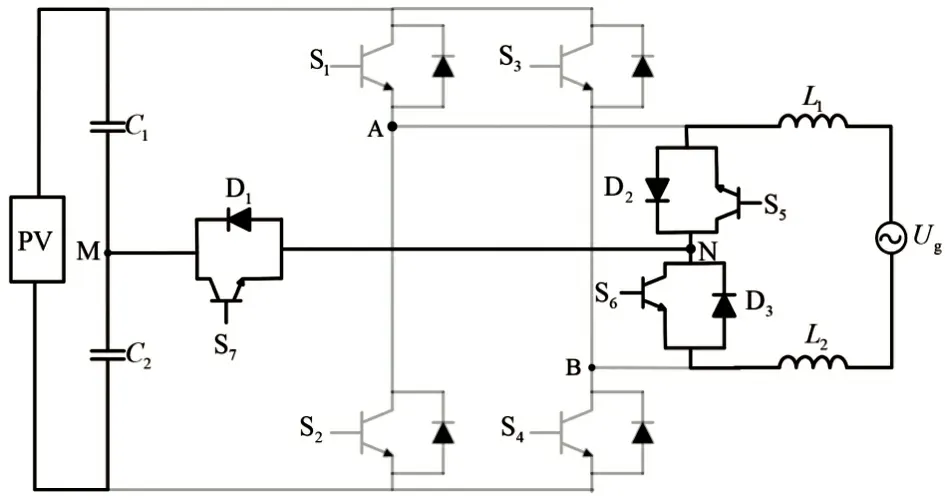
图4 正向续流工作原理

图3 中，S1、S4在信号正半周期经高频信号，开关处于打开状态，此时S2、S3处于关断状态。相应的输出电压UAN=UPV，UBN=0，共模电压为：

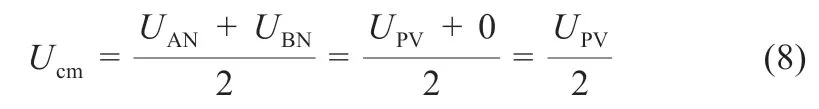
图4 中，在正向续流阶段，当UN＞UM时，开关S7处于关断状态，二极管D1正向导通，将N 点电位箝位至UM，使其等于UPV/2；当UN＜UM时，开关S7处于闭合状态，二极管D1关断，进而使得续流桥臂中点电压处于稳定状态。因此可得2UAN=UPV，2UBN=UPV，相应的共模电压为：

类似地，可以根据负半周期工作原理与反向续流时的工作原理得到相应的共模电压为：

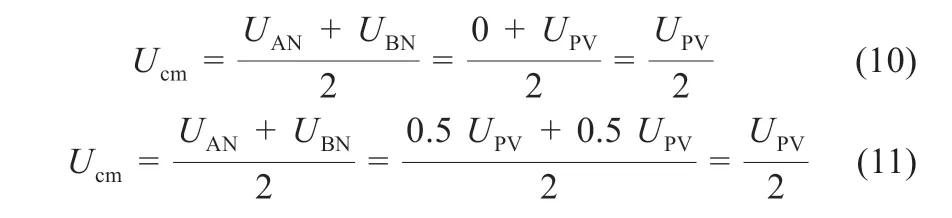
由上述分析可见，本文所提出的拓扑结构总能使共模电压恒为一个稳定不变的数值，使其幅值为光伏电源电压UPV的二分之一。因此，该TAC-Heric 控制可对漏电流进行有效抑制。

2.2 TAC-Heric拓扑仿真验证

在Matlab/Simulink 仿真平台中，根据图2 搭建新型TACHeric 拓扑仿真模型，通过单极性SPWM 信号驱动，对提出的新型TAC-Heric 拓扑进行仿真，仿真模型可以得到相应的逆变输出电压、共模电压，具体仿真参数如表1 所示。

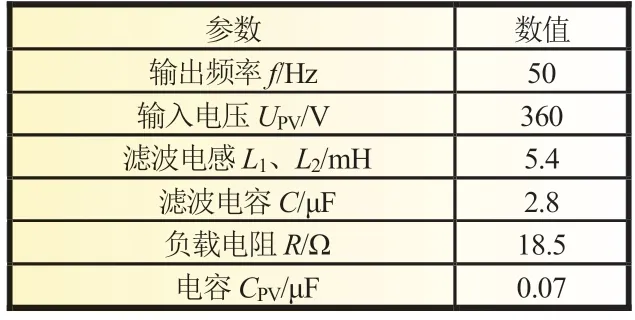
表1 TAC-Heric 拓扑逆变仿真参数

图5 为TAC-Heric 拓扑的电压输出波形，通过对中点电压的有效箝位，TAC-Heric 拓扑结构的逆变电压趋于稳定，相应的输出电压均为标准方波。图6 为基于TAC-Heric 拓扑的共模电压输出波形，共模电压保持在180 V 左右，结合式(4)，可以看出TAC-Heric 拓扑可对漏电流进行有效抑制。

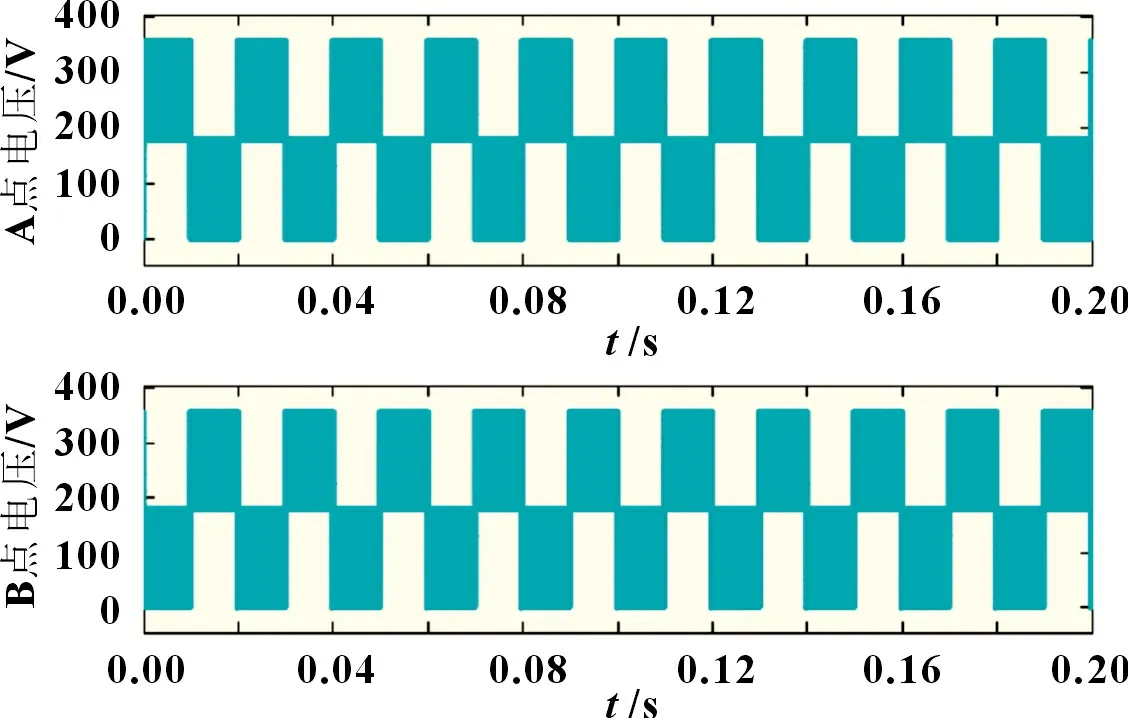
图5 TAC-Heric拓扑的电压输出波形

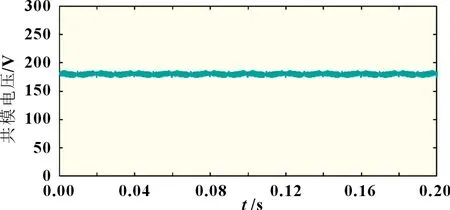
图6 TAC-Heric拓扑的共模电压输出波形

3 基于TAC-Heric 拓扑的控制分析

3.1 单相逆变器并网控制框图

光伏并网系统利用单极性SPWM 控制，对光伏阵列(PV)侧的直流输入进行调制，通过低通滤波器对逆变器所产生的电流进行滤波处理，以提供高质量的电网正弦电流波形，单相光伏逆变器拓扑控制图如图7 所示。

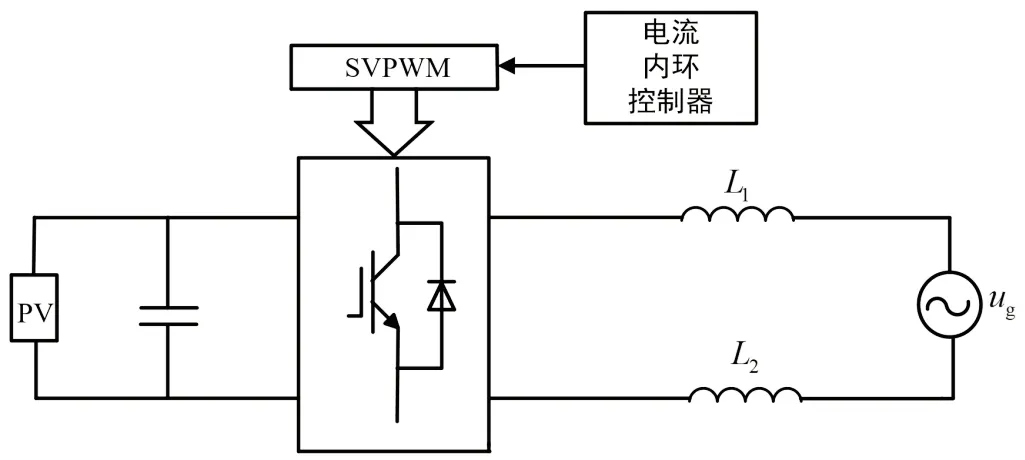
图7 单相光伏逆变器拓扑控制图

3.2 并网控制技术

在电流内环控制器中，对于传统的PI、PR 以及QPR 控制器，它们各有其特点。PI 控制具有较快的响应速度，但对高次谐波的抑制能力较差。基于PI 控制器的电流闭环传递函数为：

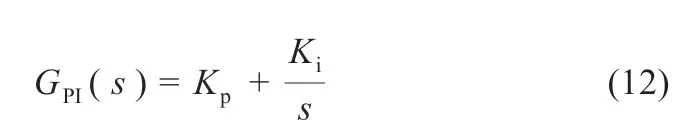
式中：Kp与Ki分别为PI 控制器的比例系数与积分系数。

PR 控制实现了对交流正弦信号的无静差跟踪调节，能对特定的谐波信号进行针对性的跟踪控制。基于PR 控制器的电流闭环传递函数为：

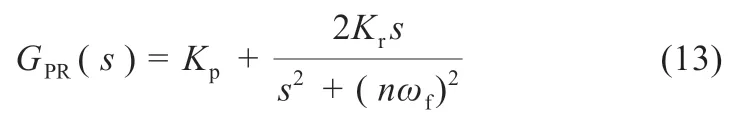
式中：Kp与Kr分别为PR 控制器的比例系数和谐振系数；n为谐波次数；ωf为基波角频率。

PR 控制的带宽较小，其对电网参数的变化十分敏感，而在电网实际运行中，电网频率可以在规定范围内进行波动，这将影响PR 控制对交流信号的跟踪控制。而QPR 控制相较于PR 控制而言，其拓展了带宽，在电网频率发生波动时，具有更好的稳定性，能更好地实现对交流信号的跟踪，基于QPR 控制器的传递函数如下：

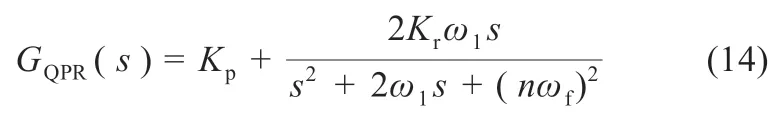
式中：ω1为谐振频率，其值与QPR 控制的带宽有关。

根据PR 以及QPR 控制的特性以及传递函数，控制器选择合适的参数为Kp=3，Kr=10，n=3，ω1=10 rad/s，可以得出其相应的Bode 图，见图8、图9。

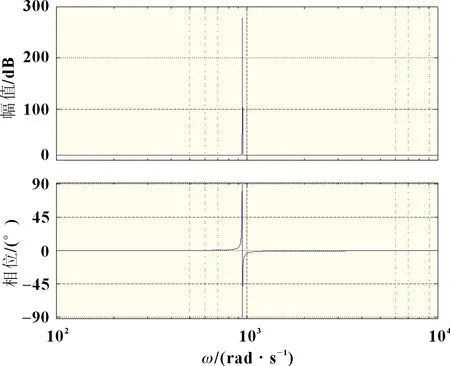
图8 PR 控制器的Bode图

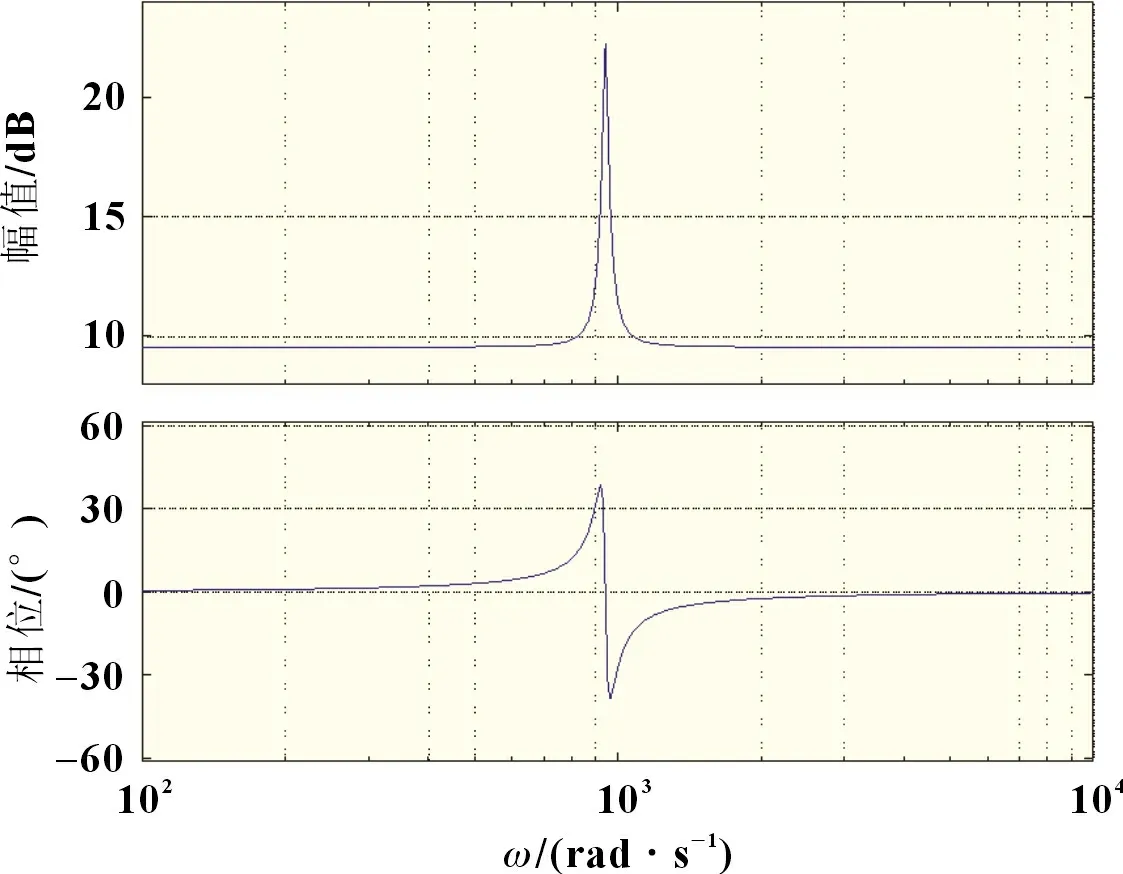
图9 QPR控制器的Bode图

从图8 可以看出，PR 控制在3 倍基波频率处表现为无穷增益，而在其他频率处的增益并不明显，因此，可以得出PR控制可以对某一些特定频率的信号进行精确跟踪。此外，PR控制的带宽非常小，在电网频率波动时，会使其对特定信号的跟踪效果变差，具有较弱的适应性，此时系统的抗干扰能力较差。从图9 可以看出，采用QPR 控制时，在3 倍基波频率处的增益虽不及PR 控制，但仍有较大增益，而且其带宽明显增加，提高了系统的稳定性。

由上述分析可知，QPR 控制对于电网参数波动具有较强的适应性，同时，为了降低电流谐波畸变率，根据QPR 控制的优势，即对特定频率的信号进行精确跟踪控制，且具有较强的抗干扰性，同时考虑PI 控制特性，即对低频分量也具有较高的增益，PI+QPR 的综合控制结构框图如图10 所示。图10中，GQPR(s)为QPR 控制的传递函数，GPI(s)为PI 控制的传递函数，Gp(s)为逆变器的传递函数，Gd(s)为滤波器的传递函数，ic(s)为特定的谐波电流信号，icref(s)为特定的谐波电流信号参考值，ig(s)为低频直流分量，igref(s)为低频直流分量参考值。

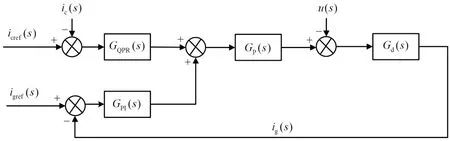
图10 PI+QPR的综合控制结构框图

3.3 TAC-Heric 逆变控制仿真分析

为验证本文所提综合控制策略的可行性与有效性，根据图7所示的单相光伏逆变器拓扑控制，利用Matlab/Simulink仿真平台建立相应的系统模型，对系统并网输出结果进行对比、分析。直流侧电压为360 V，电感L为20 mH，直流电容为1 100 μF，综合控制策略参数如下：Kp=3，Kr=10，ωf=314 rad/s，Ki=240，ω1=10 rad/s。该参数下运行Simulink 仿真模型，得到并网电压与并网电流，如图11、图12所示。

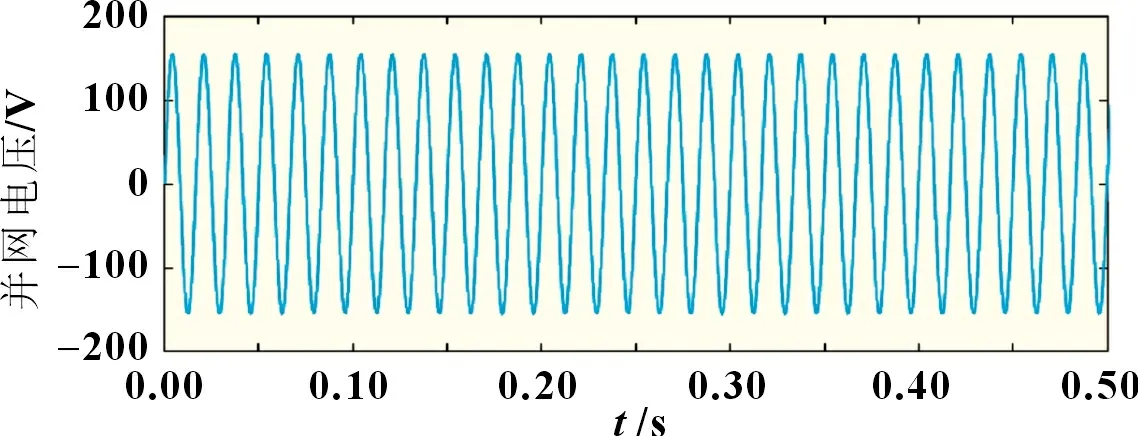
图11 PI+QPR控制下的并网电压

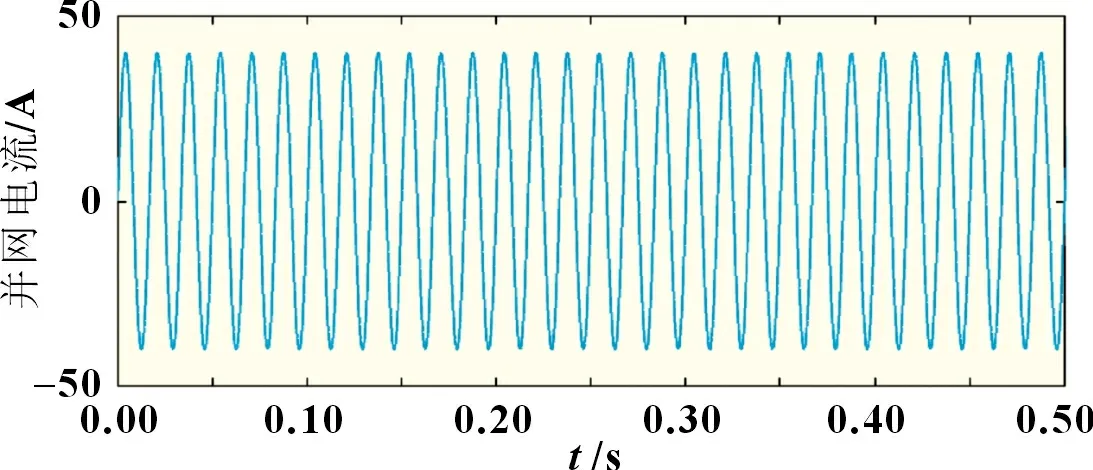
图12 PI+QPR控制下的并网电流

从图11 与图12 中可以看出，新型TAC-Heric 逆变拓扑在PI+QPR 的综合控制策略下输出的电压、电流波形质量较高，二者的幅值与相位保持一致，波动较小。

为了进一步描述综合控制策略对电流谐波抑制的能力，对PI、PR 与PI+QPR 控制下的并网电流FFT 进行分析，不同控制下的并网电流总谐波畸变率(total harmonic distortion，THD)如表2 所示。从表2 中可以看出，相较于PI、PR 控制，PI+QPR 控制的并网电流谐波畸变率更低，相应的电流输出质量更高。

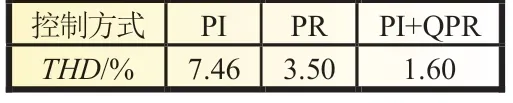
表2 不同控制方式下的THD

4 结论

在对单相并网逆变器中存在的漏电流问题进行分析的基础上，得出一种能稳定共模电压的TAC-Heric 拓扑结构，采用单极性SPWM 调制，在续流阶段对共模电压进行有效箝位，从而有效地抑制了漏电流。同时，针对TAC-Heric 的并网控制技术，在电流内环控制中，提出了一种PI+QPR 综合控制策略，使得单相并网逆变器系统具有较强的抗干扰能力，同时降低了并网电流的总谐波畸变率，提高了系统的电能质量。