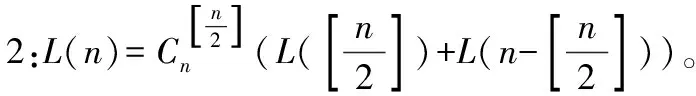关于在线性条件下NP≠P的证明

樊雪双 李云娟

1.西安思源学院基础部 陕西西安 710038；2.玛普阿大学研究生院 菲律宾马尼拉 999005

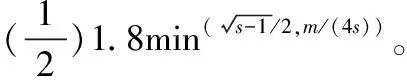
本文将利用命题公式中所含有的自由变元总次数来刻画命题公式的最简形式，且证明命题公式所含有的逻辑门个数是否可转化为多项式的等价于命题公式中所含有的自由变元总次数是否可转化为多项式。

1 基本概念及基本定理

首先给出一些必备的概念与定理。

定义1，，…，，…称为自由变元集序列，其中为自由变元的集合，且对于任意=1，2，……有⊆+1，记为{}。

定义2 对于任意，若问题真假由中的自由变元的赋值所决定，则称是上的一个问题。对于任意，其对应的命题公式记为。命题公式序列，，…，，…称为问题的公式序列，记为{}。

定义3 公式中自由变元的总次数称为的势，记为‖‖。

定义4 设公式序列{}，若存在关于的多项式()使得‖‖≤()，则称公式序列{}是势多项式的。

定义5 设公式序列{}和{}，对于任意都有⟺，则称公式序列{}和{}逻辑等价。

定义6 设公式序列{}，若存在与之逻辑等价且为势多项式的序列，则称{}是可势多项式的。

定义6设公式序列{}，若存在与之逻辑等价且为联结词多项式的序列，则称{}是可联结词多项式的。

定义7 给定公式，若公式满足以下两条，则称为的一个极小式。

与逻辑等价。

(2)不存在与逻辑等价的公式，使得‖‖<‖‖。

定义8对于命题公式，把蕴含的原子合取式称为的一个解。进一步，若不存在的解，使得⟹，且‖‖<‖‖，则称为的一个极简解。

为了对命题公式进行等价转换，引入强Demorgen转换。

定义9 对命题公式可多次利用Demorgen律，使得逻辑非下不再含有析取和合取，然后可再利用双重否定律，使得公式中每个自由变元上最多含有一个逻辑非，称该转换过程为强Demorgen转换。经过强Demorgen转换所得到的公式记为()。

显然，对于任意公式，‖‖=‖()‖。

下面说明对于任意公式序列可势多项式与可联结词多项式是等价的。

定理3 对于任意公式序列{}，其为可联结词多项式的等价于其为可势多项式的。

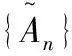
根据定理1，把判断公式序列是否为可联结词多项式的转化为判断其是否为可势多项式的。

2 类皇后问题Simqueen(n)

下面给出类皇后问题Simqueen(n)，并给出描述该问题的公式序列。

Simqueen(n)：对于一个阶0-1矩阵(元素全部为0或1)，是否可以从不同行，且不同列找到个元素全部为1。

Simqueen(n)的公式：

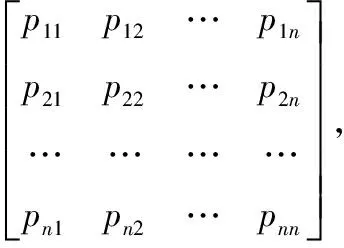
显然，当，…，为1，2…，的一个全排序时，1∧2…∧为的一个极简解。

引理1对于与Simqueen(n)的公式逻辑等价的公式，利用分配律把()展成的析取范式记为∨，若为可满足式，则具有以下性质：

至少存在一个的极简解∧…∧，其中自由变元，，…，都属于{|是中不含非的自由变元}。使得⟹∧…∧。

证明 由于是可满足式，从而中不含有同一个变元及其非。把原子合取式中出现的自由变元是否带非分为两种，把表示为：

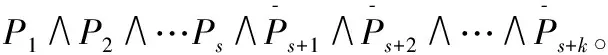
构造一个赋值={当在中出现且不带非，=1；其他=0}。

显然，|=1，从而()|=1。由于()⟺，从而|=1，即∨(∧…∧)|=1，至少存在一个极简解，，…，，使得∧…∧|=1。再由于.和∧…∧都为原子合取式，∧…∧为极简解且不含非，从而∧…∧中的自由变元只可能是，，…，中的，且⟹∧…∧。

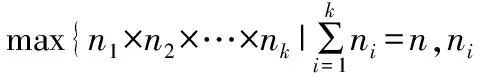
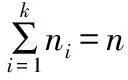
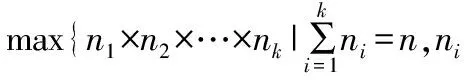
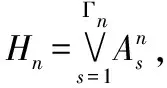
定理2 Simquee(n)的线性公式序列{}不是可联结词多项式的。

证明 假设Simqueen的线性公式序列{}是可联结词多项式的。

由定理1可知Simquee(n)的公式序列{}也是可势多项式的。那么存在势多项式公式序列{}，其中⟺且||≤()，()为关于的多项式。

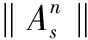
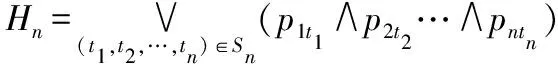
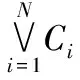
从而假设不成立，Simqueen(n)的线性公式序列{}不是可联结词多项式的。

3 关于NP与P的结论

1972年Savage在文献[10]中证明了电路规模与图灵机时间之间有一个紧密的关系。

定理3在线性条件下NP≠P。

证明 显然Simqueen(n)是一个问题，但是由定理2可知Simqueen(n)的线性公式序列{}不是可联结词多项式的，从而类皇后问题在线性条件下不能通过逻辑门的数量为多项式规模的电路来解决，从而在线性条件下≠。

4 Simqueen(n)的极小式

下面给出阶变元行列式的展开式和极小展开式概念。

记阶0-1变元矩阵为。

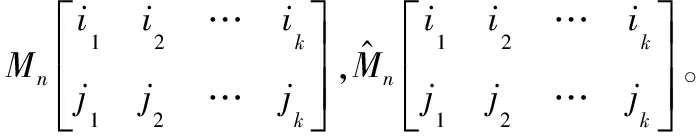
称(∧)∨(∧)为的极小展开式。

定义11对于任意，展开式和极小展开式定义如下：

在中取定个行：1≤<<…<≤，称下面公式为的一个展开式，

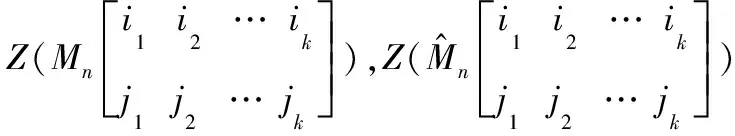
把势取最小值的展开式称为的一个极小展开式，记为()。

解 对于，的取值可以为1，2。

当=1时，按第一行展开，其展开式为:

(∧((∧)∨(∧)))∨(∧((∧)∨(∧)))∨(∧((∧)∨(∧)))

当=2时，按第一，二行展开，其展开式为：

(((∧)∨(∧))∧)∧(((∧)∨(∧))∧)∧(((∧)∨(∧))∧)

由于=1，=2，上面两个展开式的势都为15，所以上面两个展开式都为的极小展开式。

由于的任意展开式的主范式必含有且只含有的所有路径(路径中自由变元的顺序可能不同)，从而的任意展开式必与逻辑等价。接下来，考虑的极小展开式的势，记极小展开式的势为()，即()=‖()‖。

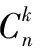
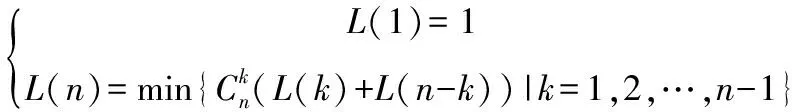
其中(1)=1显然成立。

例2求(4)的值。

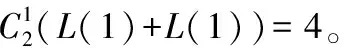
取最小值15，从而(3)=15。

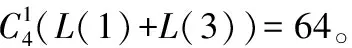
虽然关于()的关系式没有给出，但可以考虑它的取值范围。下面给出()的一个下限估计。

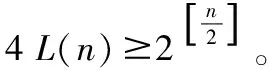
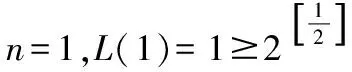
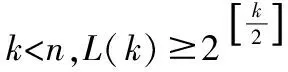
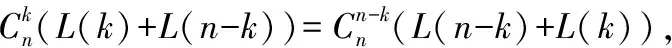
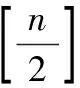
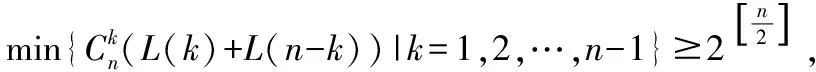
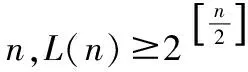
猜想1：Simqueen(n)的极小式等于()。