基于动态隶属度的模糊时间序列模型的水质预测研究*

赵春兰,李 屹,何 婷,武 刚，王 兵

(1.西南石油大学理学院,四川 成都 610500；2.西南石油大学人工智能研究院，四川 成都 610500;3.中国石油天然气股份有限公司大港油田分公司,天津 300280,4.西南石油大学计算机科学学院，四川 成都 610500)

1 引言

岷江是长江上游的重要支流之一，也是成都平原最重要的水资源，其水质与人民的生活紧密相关。由于工业废水和生活污水的排放，以及超量化肥和农药的使用，岷江的污染也日益严重。因此，对未来一段时间水质进行较为准确的动态预测是该流域水资源管理的当务之急。

国内外关于水质预测有许多模型，可以分为机理模型和非机理模型2类。机理模型是依据物质能量守恒和质量守恒原理，通过流体力学中的连续方程、运动方程和能量方程推导得出[1]。1925年美国工程师Streeter和Phelps提出的氧平衡S-P模型开创了水质模拟模型的先河，随后又出现了其他一系列水质模拟模型，如QUAL、WASP、BASINS和MIKE模型等[2]。机理模型考虑了生物化学等因素，预测精度较高，但其模型往往较为复杂，且所需采集的数据非常多。而非机理模型是指利用统计方法或人工智能方法建立的水质预测数学模型，只需对水质指标数据进行研究分析。在过去几十年中，时间序列预测法、回归分析预测法、灰色模型法、人工神经网络预测法和支持向量机等非机理模型已成功地应用于水质预测。如Sarkar等[3]利用人工神经网络模型对马图拉下游的溶解氧浓度进行了预测，取得了较好的预测效果；Kisi等[4]考虑水质数据的非线性特性，分别利用最小二乘支持向量机和多元自适应回归样条2种模型对印度Yamuna河的水质进行了预测，认为非线性预测模型有较好的预测性能；Avila等[5]使用回归分析、分类树和马尔科夫链等统计模型对游乐场水质中的大肠杆菌进行了预测研究，发现贝叶斯模型在处理缺失数据和异常值方面很灵活，并且允许实时的连续更新，是一种有参考价值的预测方法。

由于单独的预测模型大都存在一定的短板，如回归分析对数据量需求较大，泛化能力不足；BP(Back Propagation)神经网络存在收敛速度慢、容易陷入局部最优的缺点。目前国内外学者为了提高水质预测精度，通常将多种方法联合使用，以此来克服单独使用一种方法的缺点[6]。如Faruk[7]采用ARIMA(AutoRegressive Integrated Moving Average)模型与人工神经网络模型相结合的方法，提取水质数据的线性和非线性趋势，对BuyukMenderes河的水温、硼和溶解氧进行了预测，取得了比单一模型更高的预测精度；Liao等[8]将神经网络与决策树模型相结合，建立了一种改进的决策树学习IDTL(Improved Decision Tree Learning)模型，对中国最大的淡水湖之一巢湖的水质数据进行了预测，在牺牲了较小分类精度的情况下，能够为分类提供一些明确的启发式方法，提高了水质监测水平和预测能力；Liu等[9]提出了一种将实值遗传算法RGA(Real-value Genetic Algorithm)与支持向量回归SVR(Support Vector Regression)结合的混合模型RGA-SVR，对宜兴市水产养殖场水质数据进行了预测。混合模型利用实值遗传算法优化了SVR的参数，故RGA-SVR模型比BP神经网络和传统SVR模型更适合于水质预测。以上研究表明，混合方法的预测精度通常高于单独方法的，故将多种方法联合使用进行水质预测，是一种可行的提高预测精度的办法。

考虑到水质时间序列数据一般都具有季节性、非线性和模糊性等多种复杂特性，又因为传统的时序预测对数据的完整性和准确性要求较高，本文提出了一种基于动态隶属度的模糊时间序列模型。首先，将水质时间序列处理成平稳序列；其次，根据水质时间序列的特点以及模糊方法在处理不确定性问题和模糊问题的有效性，将数据模糊化，利用模糊C均值FCM(Fuzzy C-Means)聚类算法得到聚类中心和动态子隶属度序列；随后对每个子隶属度序列建立ARIMA乘积季节模型，在提取季节效应的同时预测下一个时刻的隶属度；最后去模糊化，得到水质预测结果。为了验证模型的预测效果，本文收集了岷江某断面2011年1月至2017年8月逐月监测的水质污染指标的数据，对水质进行了未来3个月的预测分析，并与ARIMA乘积季节模型和经典模糊时间序列FTS(Fuzzy Time Series)模型进行了对比分析。

2 水质预测模型

2.1 ARIMA乘积季节模型

由于水质数据表现出明显的季节性特征，故本文采用ARIMA乘积季节模型作为对照。简单的季节模型认为序列的季节效应、长期趋势和随机效应之间是很容易分开的；但乘积季节模型认为序列的长期趋势、季节效应和随机效应之间相互影响，且它们之间的关系比较复杂[10]。

ARIMA乘积季节模型的建模思路为：对序列进行d阶差分和D阶以周期S为步长的差分运算；当序列仍然存在短期相关性时，使用低阶ARIMA(p,d,q)提取短期相关性，p和q分别表示非季节自回归阶数和移动平均阶数；当序列还存在季节效应时，则使用以周期步长为单位的ARIMA(P,D,Q)模型提取相关关系，P和Q分别表示季节自回归阶数和移动平均阶数。

此时拟合的模型为2个模型的乘积，如式(1)～式(5)所示：

(1)

θ(B)=1-θ1BS-θ2BS-…-θqBS

(2)

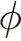
(3)

ΘS(B)=1-Θ1BS-Θ2BS-…-ΘQBS

(4)

ΦS(B)=1-Φ1BS-Φ2BS-…-ΦPBS

(5)

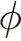
ARIMA模型常用于时间序列预测，经典的ARIMA模型预测流程可分为3步：首先对原始数据进行ADF(Augmented Dickey-Fuller)平稳性和白噪声检验，若非平稳，可进行差分处理；其次根据AIC(Akaike Information Criterion)最小准则进行模型的识别与定阶；最后对ARIMA(p,d,q)模型进行参数估计与检验,模型的建立与预测流程如图1所示。参数估计常用的方法有最大似然估计、无约束最小二乘法和条件最小二乘法[11]。本文采用条件最小二乘估计法对模型的参数进行估计。

Figure 1 The modeling &predition of ARIMA model图1 ARIMA模型建模和预测流程

2.2 经典模糊时间序列预测模型

1994年，Song等[12,13]运用模糊集合、隶属函数等概念，对时间序列数据建立了经典的模糊时间序列预测模型(FTS)，随后该模型及其改进模型被广泛地应用于各个领域。考虑水质数据存在模糊性的特点，本文将水质数据模糊化后再进行预测分析。

定义1[12,14]设U为论域，且U={u1,u2,…,un} 是给定U上的一个次序分割集，定义A为U上的语义变量集(模糊集)，如式(6)所示：

(6)

或表达为向量形式，如式(7)所示：

A={fA(u1),fA(u2),…,fA(un)}

(7)

其中,fA(·)是模糊集A上的模糊隶属度函数，且fA(·):U→[0,1];fA(ui)是ui在模糊集A上的模糊隶属度值，且有fA(ui)∈[0,1],1≤i≤n。

定义2[12,14]设Z(t)(t=0,1,2,…)为实数域R的一个子集，Z(t)上定义了一组模糊集fi(t)，假设F(t)={f1(t),f2(t),…}，称F(t)为Z(t)上的模糊时间序列。

这里的F(t)为语言变量，fi(t)为F(t)中可能的语言值，即定义1中的fA(ui)。因为对于不同的时刻t，F(t)是不同的，故F(t)为t的函数。

定义3[12,14]设R(t,t-1)为从F(t-1)到F(t)的模糊关系，且满足F(t)=F(t-1)∘R(t,t-1)，则称F(t)是由F(t-1)通过模糊关系R(t,t-1)推导得到的，其中“∘”代表合成运算，关系R(t,t-1)称为定义在F(·)上的一阶模糊关系。

定义4[12,14]设F(t)是一个模糊时间序列。令F(t-1)=Ai，F(t)=Aj，这2个连续的观测值F(t-1)和F(t)之间可以用一个模糊逻辑关系来表示，记为Ai→Aj，其中Ai和Aj分别被称为“左件”和“右件”，Ai对应第i个模糊概念。

定义5[12,14]定义关系矩阵R的运算方法如式(8)所示：

R=R(t,t-1)=∪i,jRi,j

(8)

经典的模糊时间序列建模步骤一般为：

(1)根据序列确定论域U，对U进行划分。为方便计算，基于序列的最小值和最大值，对最小值向下减一个合适的正数，最大值向上加一个合适的正数，将得到的2个数作为区间的2个端点，该区间也即论域，随后对论域进行等间距的模糊划分。

(2)定义模糊集和数据模糊化。论域U被划分成了k个子区间，相对应地就有k个模糊概念Ai。根据相应的隶属函数，求出数据对每个模糊集的隶属度向量，并将数据模糊化为最大隶属度所对应的模糊集。

(3)建立模糊逻辑关系并确定模糊关系矩阵。基于数据的模糊概念及其出现的先后顺序，建立模糊逻辑关系。根据定义5可求得模糊关系矩阵R。

(4)去模糊化后进行预测。选择合适的去模糊化方法，将输出去模糊化后得到的预测值。

本文参照国家的水质分类标准，将序列等分为5个模糊区间，按照I和II 类的水质为优、III 类的水质为良、IV 类的水质为轻度污染、V 类的水质为中度污染、劣 V 类的水质为重度污染进行划分，随后根据上述步骤进行预测分析。

3 基于动态隶属度的模糊时间序列模型

3.1 基本思想

时间序列ARIMA模型基础理论完善，方法简单易行，但模型的建立依赖于数据，要求数据完整且较为精准，而且在预测中主要考虑了时间因素，忽略了引起序列本身变化的一些不确定因素。但是，某些水质数据存在固有的不确定性问题，例如测量不准确、观测集不完整或难以获得测量值等[13]。模糊时间序列预测模型作为常用的不确定信息处理方法，为水质预测开辟了新路径。但是，经典的模糊时间序列模型对实现步骤的要求较高，其预测步骤所应用的方法不同也会对预测结果造成很大的影响。根据国内外学者将不同模型结合以提高模型性能和预测精度的经验，以及水质数据本身的模糊性和季节性特性，本文结合时间序列分析和模糊理论，提出了一种基于动态隶属度的模糊时间序列预测模型。该模型以模糊时间序列预测模型为基础，将ARIMA 模型加入其中，对隶属度进行动态的季节性预测，简化运算步骤的同时还提高了预测精度。

3.2 模糊C均值聚类算法

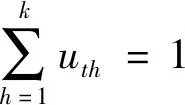
(9)

其中，N为样本总数;k为聚类数目，在本文中即k个模糊概念;m是控制模糊重叠程度的模糊划分矩阵指数，且m>1;‖xt-ch‖表示t时刻的样本值xt到聚类中心ch的欧几里得距离;uth表示样本xt对第h个聚类的隶属度。引入拉格朗日参数λ，利用拉格朗日方法对以上问题求解，令拉格朗日函数如式(10)所示：

(10)

令∂F/∂uth=0,∂F/∂λ=0,通过一系列计算，可以得到聚类中心,如式(11)所示：

(11)

隶属度函数如式(12)所示：

(12)

由此可以得到FCM算法的步骤为：

(1)随机初始化聚类成员值uth；

(2)利用式(11)计算聚类中心，按最小距离的原则进行聚类；

(3)根据式(12)更新隶属度uth的值，通常情况下，m的值取为2；

(4)计算目标函数Jm的值；

(5)重复步骤2～步骤4，直到Jm的值小于指定的最小阈值，或者达到最大迭代次数之后停止迭代，得到最后的聚类结果;

(6)确定聚类个数k后，利用上述步骤，便可以得到k个聚类中心。

3.3 模型预测步骤

模型的预测步骤主要包括：原始数据平稳化、构建论域并划分子论域、模糊化数据、子隶属度序列时间序列预测、去模糊化得到预测值。图2展示了其预测流程,具体执行步骤如下所示：

(1)原始数据平稳化。

判断序列是否为平稳序列，若非平稳，则需要通过差分化处理得到平稳的序列用于后续分析，以确保后续分析的有效性和准确性。

(2)构建论域并划分子论域。

找到建模数据中的最大值DMax和最小值DMin，为方便划分论域，选择2个合适的正实数d1和d2，则得到论域U={DMin-d1,DMax+d2}。

利用式(10)确定聚类个数：

(13)

其中，N为样本总数;xt和xt-1分别为t时刻和t-1时刻的样本值。

将聚类中心按从小到大排序，可得到聚类中心c1,c2,c3,…,ck,设聚类中心ch和ch+1之间的中点为bh，那么bh就为子论域的边界值。假设子隶属度序列为Y={Y1,Y2,…,Yk}，则它们的论域分别为：u1:[DMin-d1,b1],u2:[b1,b2],u3:[b2,b3],…,uk:[bk-1,DMax+d2]。

(3)模糊化数据。

FCM聚类算法在得到聚类中心的同时还得到一个隶属度矩阵(uht)k×N(1≤h≤k,1≤t≤N)，如式(14)所示：

(14)

在隶属度矩阵中，每一行代表每个子论域所对应的子隶属度序列。假设u12是第2列中数值最大的值，就代表原始序列的第2个值隶属于第一个论域的程度最大，矩阵中其他数值的意义依次类推，即：

Y1={u11,u21,…,uN1},

Y2={u12,u22,…,uN2},

⋮

Yk={u1k,u2k,…,uNk}

(15)

其中,uth(t=1,2,…,N;h=1,2,…,k)是样本xt对区间uh的隶属度，且uth∈[0,1]。

(4)子隶属度序列的时间序列预测。

平稳序列X={x1,x2,…,xN}通过FCM聚类算法中的k个隶属度函数模糊化后，得到k个子隶属度序列Y={Y1,Y2,…,Yk}。分别对每个子隶属度序列进行时间序列预测，并利用ARIMA乘积季节模型提取季节趋势,若乘积季节模型无法拟合，则选择传统的ARIMA(p,d,q)模型进行隶属度的预测。

(5)去模糊化得到预测值。

FCM算法可得到k个聚类中心c1,c2,c3,…,ck，则利用如式(16)所示的隶属度加权平均法得到预测值G(t)：

(16)

其中，fth表示t时刻对应的数值隶属于第h个模糊集的程度，即隶属度。

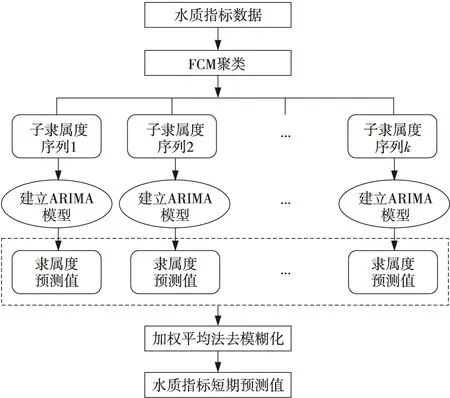
Figure 2 Flow chart of model prediction图2 模型预测流程图

4 实证研究

4.1 预测指标选取

本文对岷江某断面2011年1月至2017年11月共83个月逐月监测的6项指标的水质数据，按照国家规定的《地表水环境质量标准》(GB3878-2002)中相应的评价标准进行评价，利用最常用的单因子法对其逐月评价完毕之后发现，其中溶解氧与总磷的污染较为严重，于是确定再对这2个水质指标进行预测分析，以达到污染防治的目的。原始数据如表1所示，其中，前80个样本点作为模型训练集，后3个样本点作为模型预测集。

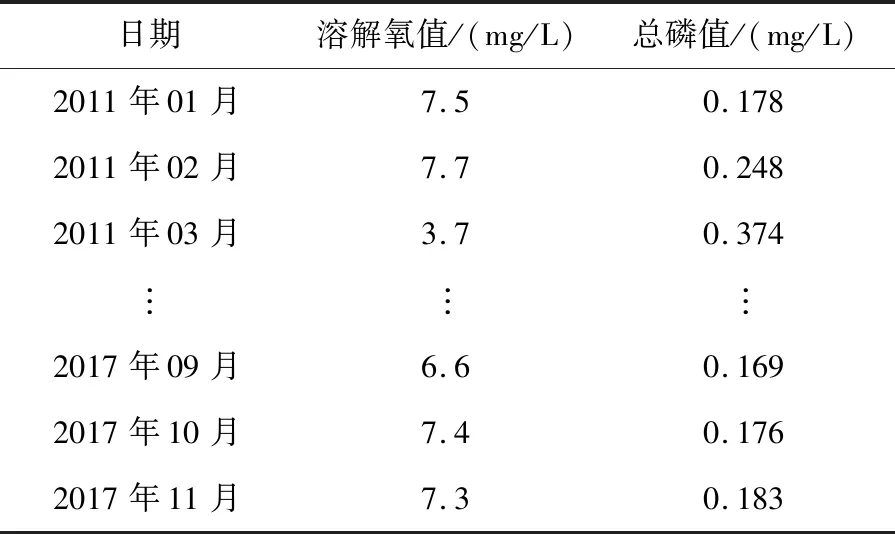
Table 1 Water quality indicator data表1 水质指标数据

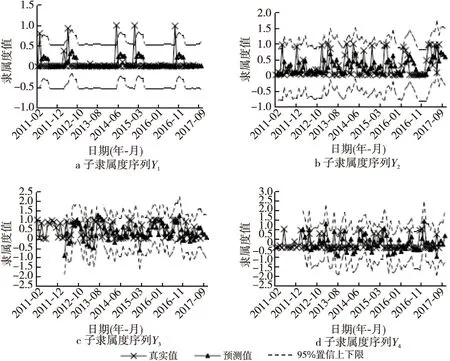
Figure 3 Time series fitting diagrams of dissolved oxygen sub-membership series图3 溶解氧数据子隶属度序列时间序列拟合图

4.2 模型预测性能评价指标

为了更科学准确地评价预测效果，并比较不同模型的优劣，本文选用式(17)～式(19)所示的3个指标来评价模型的预测性能。

(1)均方根误差(RMSE)：

(17)

(2)平均绝对误差(MAE):

(18)

(3)平均绝对百分误差(MAPE):

(19)

4.3 实例分析

本节以溶解氧数据为例展示模型的预测过程，总磷的预测过程同理。将溶解氧数据进行一阶差分得到平稳数据后，计算聚类个数，并利用FCM聚类算法中的隶属度函数，得到4个子隶属度序列如表2所示。随后对这4个子隶属度序列Y1,Y2,Y3和Y4依次进行传统的时间序列分析。

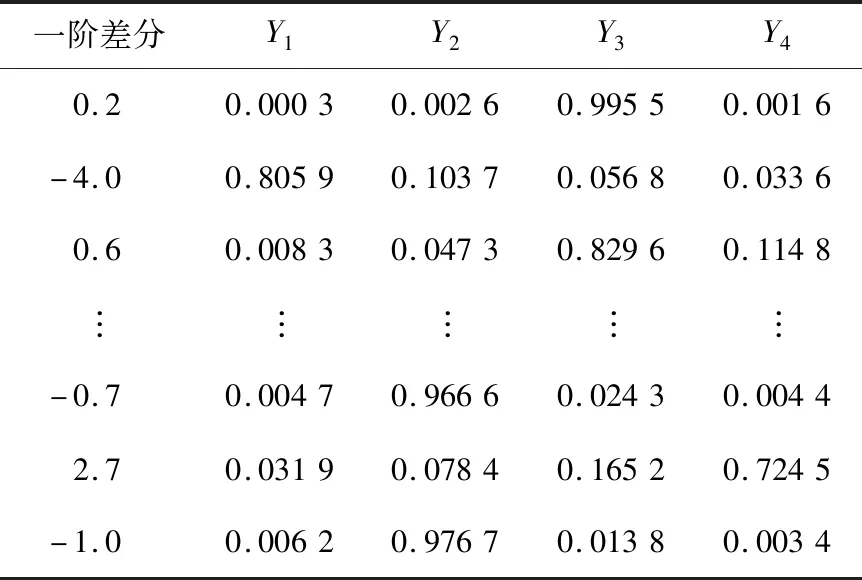
Table 2 Dynamic sub-membership sequence表2 动态子隶属度序列

对4个子隶属度序列按照2.1节中的流程进行预测，分别拟合如下模型：

Y1:ARIMA(3,1,0)

Y2:ARIMA(3,1,0)

Y3:ARIMA(0,1,1)×(0,1,1)12

Y4:ARIMA(1,1,0)×(1,1,0)12

可得到4个子隶属度序列的拟合效果,如图3所示。

通过对4个子隶属度序列的预测，得到每个子隶属度序列最后3个月的预测值以及去模糊化之后的值,如表3所示。表3中每一行的值表示同一个预测点隶属于不同子论域的程度，每一列的值表示不同预测点隶属于同一个子论域的程度。利用式(16)对每一行进行去模糊化操作，得到的值如表3最后一列所示，该值表示每一个点去模糊化后的真实预测值。将预测值还原到差分前的值，可得到原始数据后3个月的预测值。

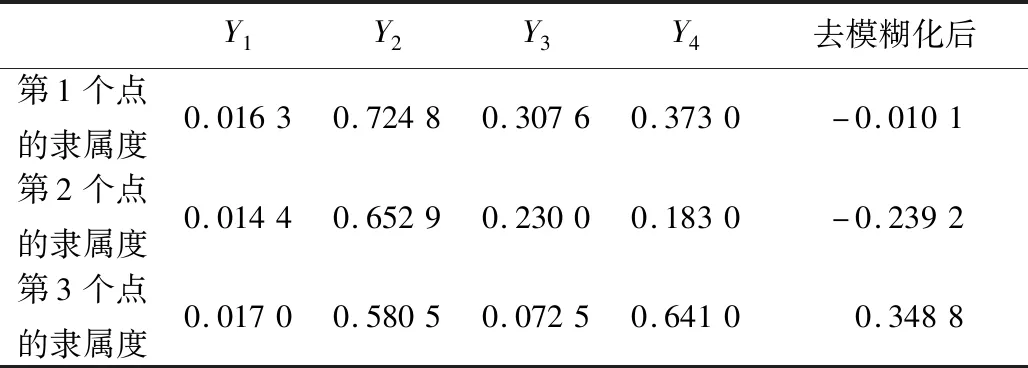
Table 3 Predicted values of membership表3 隶属度预测值

4.4 结果评测与分析

为比较本文所提的新模糊时间序列模型与其他模型对水质指标的预测效果，表4给出了不同模型对不同水质指标的预测结果。对预测结果进行可视化分析，得到模型预测的走势图,分别如图4和图5所示。

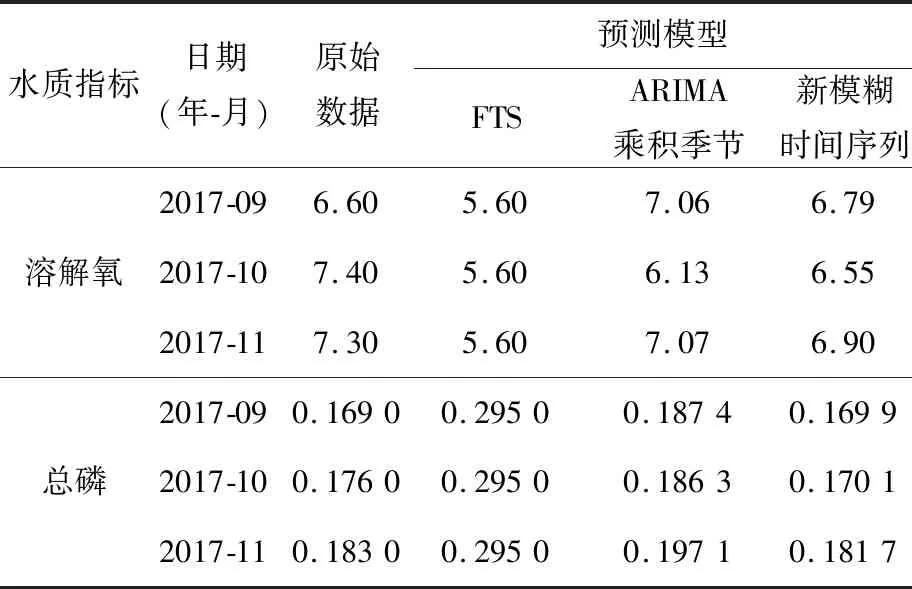
Table 4 Model prediction results表4 模型预测结果

Figure 4 Prediction trend of dissolved oxygen图4 溶解氧预测走势图

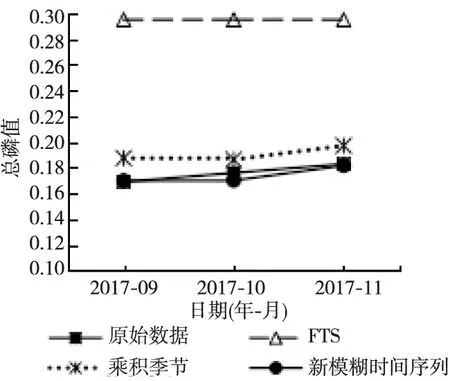
Figure 5 Prediction trend of total phosphorus图5 总磷预测走势图

从图4和图5可以看出，对2个水质指标未来3个月的预测中，基于动态隶属度的新模糊时间序列模型的预测值与真实值的偏差最小，说明该模型拟合最好。

为更科学贴切地反映预测效果，利用前文所述的3个评价指标，分别对上述3个模型进行评价,如表5所示。3个指标的评价结果表明：本文构建的基于动态隶属度的模糊时间序列预测模型的预测性能最好，预测误差指标均优于其他对比模型的。

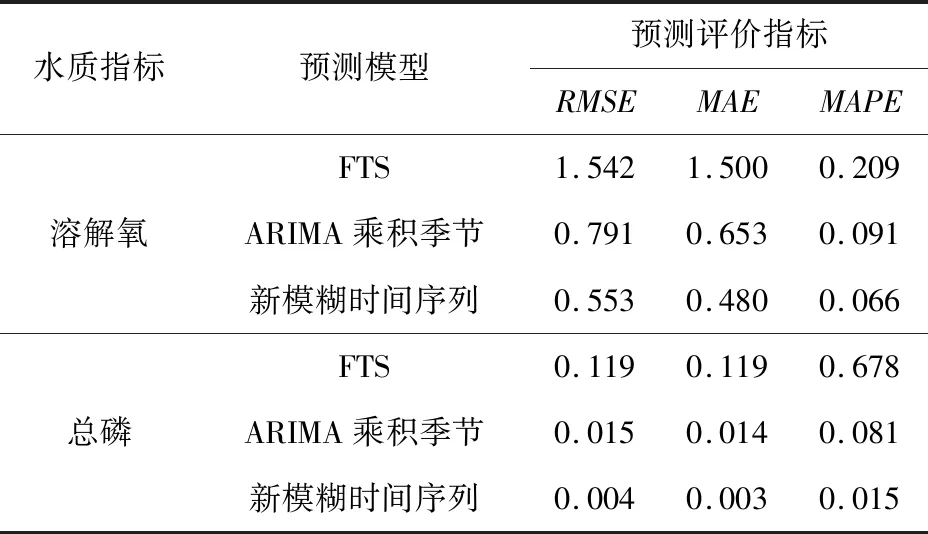
Table 5 Comparison of prediction error indicators of various models表5 各模型预测误差指标的比较

将评价指标的结果进行可视化分析如图6所示。从图6可以看出，基于动态隶属度的新模糊时间序列模型的预测精度最高，表明其预测效果最好，其次由于ARIMA乘积季节模型能提取较为复杂的季节效应，其预测效果次之，经典的模糊时间序列预测模型效果最差。就3种评价指标而言，本文提出的模型预测的溶解氧的RMSE相对于FTS和ARIMA乘积季节模型分别提高64.1%和30.1%，MAE分别提高68.0%和26.5%，MAPE相对于FTS和ARIMA乘积季节模型分别提高68.4%和27.5%。而预测的总磷的RMSE、MAE和MAPE都远小于其他对比模型的。故本文根据水文时间序列的特点，将数据模糊化后再利用ARIMA乘积季节模型进行动态隶属度的预测，并尽量建立ARIMA乘积季节模型提取隶属度序列的季节趋势，成功地提高了预测精度。

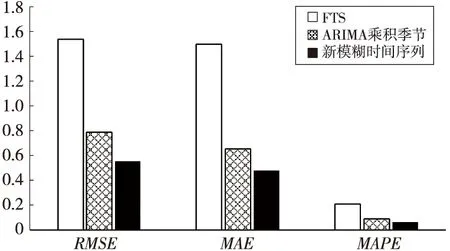
Figure 6 Comparison of evaluation results of dissolved oxygen prediction accuracy图6 溶解氧预测精度评价结果柱状图对比

5 结束语

针对复杂多变的水质时间序列，本文基于时间序列分析方法和模糊数学基础理论，提出了一种基于动态隶属度的模糊时间序列预测模型。首先采用模糊C均值聚类将平稳的序列进行论域划分，既避免了经典的模糊时间序列中等分导致的数据分布不均匀问题，也考虑到了水质数据属于各个污染类别时存在的亦此亦彼性；其次，将数据模糊化后得到的动态子隶属度序列进行传统的时间序列预测，充分结合了水质数据的模糊性特点和传统时间序列预测法在处理动态时间序列上的优点，克服了传统时间序列预测方法要求数据较为完整和精确的弊端,与经典的模糊时间序列模型相比，无需建立模糊逻辑关系矩阵，大大简化了计算过程。将新模型对污染较为严重的总磷和溶解氧的预测结果与FTS、ARIMA乘积季节模型的预测结果分别进行了比较，预测结果表明，新模糊时间序列模型的预测精度相对于其他2种模型的有较大的提高，是一种有效的短期预测模型，可为水质预警与保护提供有价值的参考。另外，是否有更加适合水质数据的模糊化方法?其他人工智能方法(如神经网络和支持向量机)能否与该方法进行结合，从而进一步提高预测模型的精度?今后将在这方面进行更深入的探索分析。