一种具有身份锁的门限多秘密共享方案*

崔晨雨，张丽娜,2

(1.西安科技大学计算机科学与技术学院,陕西 西安 710600;2.陕西师范大学计算机科学学院,陕西 西安 710119)

1 引言

秘密共享技术是应用密码学中一项非常重要的技术，在信息安全存储、传输及安全计算等环节起着关键作用。秘密共享问题，就是如何利用密码技术将秘密信息进行分割存储，以防止权力过于集中，达到分散风险和容忍入侵的目的。门限秘密共享方案[1]自1979 年提出以后，秘密共享技术开始迅速发展，许多研究人员都投入了大量精力对共享方案及其相关应用进行深入研究，目前提出的门限共享方案有很多种，主要代表有Shamir[1]的 Lagrange插值多项式方案、Blakley[2]的矢量方案、Asmuth等[3]的同余类方案和Karnin等[4]的矩阵法方案。文献[5]提出了一种基于广义中国剩余定理GCRT(Generalized Chinese Remainder Theorem)的主动多秘密共享方案，相比其他共享方案，该方案添加了共享刷新阶段，在满足多秘密不变的前提下，在固定时间内更新无序份额使方案具有更高的安全性。此外，在秘密恢复阶段，该方案使用基于广义中国剩余定理的轻量级算法，使得恢复过程具有更小的计算负载。文献[6]提出了一种基于通用共享的多秘密图像安全共享方案，利用二进制运算从n个秘密图像中生成n个共享并同时生成通用共享，同时用函数确定恢复秘密的阈值，增大了共享的随机性，提供了一种计算效率高且安全的方案。

目前秘密共享研究着重解决欺骗行为检测以及子秘密不可重复使用问题。Shamir和Blakley等人的方案为门限方案奠定了基础，但不能杜绝秘密分发者与分享者的欺骗行为。针对门限方案在实际应用中可能存在欺骗行为的问题，文献[7]提出了一种基于特征值的安全可验证的门限秘密共享方案，在基本Shamir门限方案的基础上，从矩阵特征值的角度出发，利用n阶矩阵的特征方程具有重根的特点设计了一种可验证的秘密共享方案。该方案被证明是安全的，可以抵抗参与者和分发者的恶意欺骗。文献[8]提出了一种基于埃尔米特插值法的、无可信中心、可公开验证、可更新的多秘密共享方案。该方案利用了基于双线性对的零知识证明，具有可同时对秘密份额和更新份额进行公开验证的优点。针对门限方案在实际应用中经常存在多秘密共享的问题，为了使份额可以在子秘密中重复使用，文献[9]提出了一种基于单向函数的伪份额，在秘密恢复过程中并没有直接使用这些秘密信息，而是使用双变量单向函数对其计算结果。尽管每个参与秘密恢复的参与者都提供了一个由其子秘密份额计算的伪份额，但根据双变量单向函数的安全性质，该伪份额不会披露其真正的秘密份额，因此子秘密可重复使用。文献[10]提出了一种安全的使用门限多秘密共享方案，基于中国剩余定理将多项式产生的子秘密信息进行聚合生成公开值，减少了公开值的个数，参与者只需存储1个子秘密且子秘密可以多次使用。但是，文献[5-10]中的方案都没有考虑不同秘密访问控制权限改变的问题，不适用于复杂场景。

在实际应用中，秘密共享系统只考虑秘密分发过程中的欺骗行为和子秘密可重复使用是不够的，还需要考虑对不同秘密的访问控制结构[11]发生改变的问题，这也是目前在设计和实现秘密共享方案时需要解决的关键问题之一。满足访问控制结构可更改的方案能将门限多重秘密共享应用于复杂场景中，如电话会议和文件分发等。

简单的多秘密共享方案是针对不同秘密存在不同的份额进行恢复，在n个参与者中，只要出现t个或t个以上的参与者共同合作就可以恢复秘密。但在实际生活中，为应对复杂场景，对于不同秘密应该设计不同的访问控制权限。本文设计的秘密共享方案是在用户集合{U|u1,u2,u3,…,un}的基础上设置访问结构ξ，它是由用户集合U中的一些子集G组成的，且满足子集G可以重构秘密K，称子集G为秘密K的授权子集[12]。

以有30人的某公司的一次秘密文件分发过程为例，分发者需把秘密文件1和秘密文件2分别发给公司的7个高层和23个员工，要求文件1只能由高层恢复，文件2只能由员工恢复。分发者对文件1和2的份额进行加密，为防止出现人员监守自盗、遗忘密钥或因人员缺席而无法恢复文件等各种问题，要求参与的人员至少满足门限值5才可恢复出秘密文件，本例中普通员工与高层的访问权限不同，员工中任意5人或多于5人只能恢复文件2且无法恢复文件1，同理高层只能恢复文件1。限定一个新的用户子集作为新的授权子集，定义一种具有身份锁的(t,j)门限方案，如图1所示。

针对不同的秘密，分发者会根据授权子集计算新的锁X，不同秘密对应不同身份锁，因此本文方案可适用于门限多秘密共享。首先如图1a所示，分发者对全体参与者分发基础份额(每个参与者都有)；其次，如图1b所示，分发者对秘密K所对应的授权子集G中的用户分发秘密份额(不在授权子集中的参与者没有)；最后，如图1c所示，秘密K对应的授权子集中的参与者通过自己的基础份额和秘密份额来恢复门限，当且仅当参与的人数达到门限t时可恢复秘密。

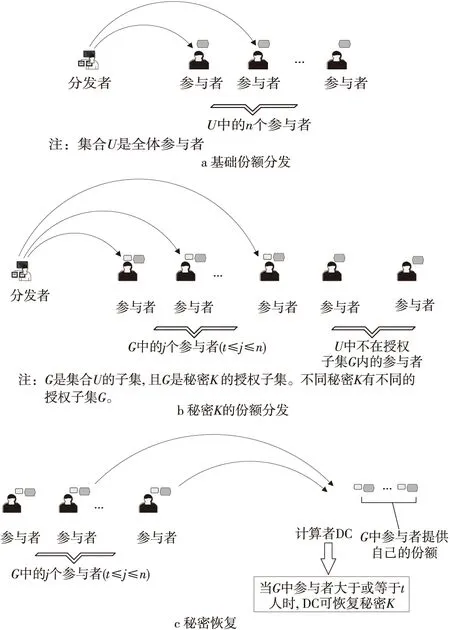
Figure 1 (t,j) threshold scheme with identity lock图1 具有身份锁的(t,j)门限方案

鉴于以上考虑，本文提出一种具有身份锁的门限多秘密共享方案，在保持子秘密可重复使用以及可检测欺骗行为的前提下，不增加参与者信息交互量，仍可有效地解决秘密共享技术中对不同秘密的访问控制结构发生改变带来的问题；同时，该方案也不需要预设安全通道来传输秘密份额，具有很好的安全性和实用性。

本文的贡献在于利用CRT(Chinese Remainder Theorem)构造了安全锁，设计了一种综合性能较好的多秘密门限分享方案。该方案主要有以下特点：(1)基础子份额可重复使用并可离线验证；(2)不同秘密对应不同授权子集，并引入参数验证参与者身份，减少无效用户盲目计算；(3)不需要预设安全通道；(4)参与者可检测秘密分发者的欺骗行为。

论文的组织安排如下：第2节介绍本文多秘密共享方案相关预备知识；第3节给出了基于CRT构造的安全锁，并在此基础上提出多秘密共享方案，并对基础子份额分发、秘密的份额分发、基于CRT的身份锁构造、秘密恢复等模块进行详细介绍；第4节主要从正确性、安全性、欺骗检测和性能等4个方面进行分析；第5节给出本文的结论。

2 预备知识

本文在给出方案之前，首先介绍需要用到的一些符号及其定义、中国剩余定理[13]和带锁的会话密钥[14]等相关知识。

2.1 符号说明

Table 1 Parameters and their definitions表1 参数及其定义

2.2 中国剩余定理

设整数N1,N2,…,Nn为两两互质的正整数，则对于任意的整数R1,R2,…,Rn,满足如式(1)所示的同余方程组：

(1)

2.3 带锁的会话密钥

锁是一个保护机制，只有满足锁的要求才能够打开锁得到会话密钥。

定义1秘密分发者(Dealer)指把1个或t个秘密S1,S2,…,St分发给n个秘密分享者的人或服务器，称秘密分发者为Pd。

定义2假设系统存在一个公告栏NB(Notice Board)用来存放公开参数，系统各方均可访问NB上的内容，但只有Pd才能修改或更新NB上的内容。

定义3假设本文系统中存在一个用户集合{U|u1,u2,u3,…,un}，且U包含了系统中的所有用户。存在用户子集合G1,G2,G3,…,Gt且Gi是U的子集(满足|Gi|≤|U|)，对于不同的秘密Si有不同的用户集合Gi与之对应。存在X锁满足对于不同秘密Si只能由对应用户集合Gi中的用户打开，而系统中的其他用户无法打开，且X锁依赖于秘密Si，也就是说针对不同的秘密Si会存在不同的X锁，如图2所示。

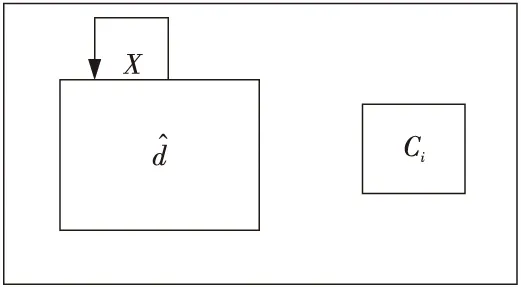
Figure 2 Locked session key图2 带锁的会话密钥

3 本文方案构成

本文提出的具有身份锁的门限多秘密共享方案包含4个模块：基础子份额分发、秘密份额分发、基于CRT的身份锁构造和秘密恢复。此外，本文还提出了多秘密共享方案的具体实施步骤。图3为本文方案的框架图。

Figure 3 Schematic diagram of the scheme in this paper图3 本文方案框架图

3.1 基础子份额分发

定义4定义2个q阶的循环群分别为(A1,+)和(A2,·)，且p为A1的生成元，令e为A1和A2上的双线性变换[15]，即e:A1×A1→A2。

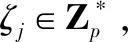
算法1公私钥对生成

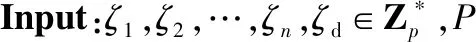
Output:Qj(j=1,2,…,n)和Qd。

1ifP∈uj(j=1,2,…,n)then

2Sj=h0(ζj);

3Qj=Sj*p;

4else

5Sd=h0(ζd);

6Qd=Sd*p;

7end

8returnQj(j=1,2,…,n) andQd

算法1中P是参与者，基础子份额是用户集合中所有用户都具有的份额，本文方案不预设安全通道传输基础子份额，分发者和参与者先利用双线性变换和公开参数进行会话密钥的协商，再通过协商的密钥分发基础子份额。分发者通过会话密钥对基础子份额进行加密，并公开加密后的密文用于参与者的验证。分发者基础子份额分发算法如算法2所示。

算法2分发者基础子份额分发

Input:xj,bj,Qj(j=1,2,…,n),P,h1和hk。

Output:cj,sj,Rj(j=1,2,…,n)。

1ifP=Pdthen

2mj=h1(e(Qj,p)bj);

3rj=hmj(xj);

4cj=Emj(xj‖rj);

5Rj=rj*Qd;

6sj=bj*p-rj*Sd;

7end

8returncj,sj,Rj

参与者用NB上的参数和自己私钥计算会话密钥，并对验证公开参数。若验证通过，则解密得到有效的基础子份额,如算法3所示。

算法3参与者基础子份额计算

Input:cj,sj,Rj,Sj,Qj(j=1,2,…,n),P,h1和hk。

Output:xj(j=1,2,…,n)。

1ifP∈uj(j=1,2,…,n)then

2mj=h1(e(Qj,sj)e(Sj,Rj));

3Dmj(cj)=xj‖rj;

5returntrue;

6end

7end

8returnxj

本文利用双线性变换和公开参数实现会话密钥的协商，在此基础上对基础子份额进行安全分发和正确性验证。基础子份额分发步骤如下所示：

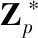
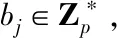
Step3秘密分发者Pd利用公开的带密钥的单向函数hk和mj，计算rj=hmj(xj),cj=Emj(xj‖rj),Rj=rj*Qd,sj=bj*p-rj*Sd，并在NB上共享参数(cj,sj,Rj)。

Step4每个参与者uj从NB上获取cj和Rj来计算mj=h1(e(Qj,sj)e(Sj,Rj))。

3.2 秘密份额分发

本文设计中，对于不同秘密存在不同用户子集{Gi|gi1,gi2,gi3,…,gij}，且满足j≤n。秘密分发者对份额上锁X(X匹配Gi中的用户)。不同的秘密存在对应的锁和份额，且只有满足Gi中的用户提供的份额个数大于t时，才可以恢复出秘密Si，其中t为门限秘密恢复的阈值。

定义6f(x,y)为一个双变量单向函数[16]，即给定两个自变量会生成一个变量，且函数不可逆。

本文以Shamir方案为基础，将秘密隐藏于常数项，引入随机数x0对基础子份额进行更新，使得基础子份额可重复使用。秘密份额的参数分发算法如算法4所示。

算法4秘密份额的参数分发

Input:c1,c2,g(x)=K+a1x+a2x2+a3x3+…+at-1xt-1,ω,N1,N2,…,Nn,f(x,y),x0。

Output:x0,kij,Rij,ω,ωK,ωa1,ωa2,ωa3,…,ωat-1,Xj。

1ifP=Pd&&uj∈Gthen

2 calculateωK,ωa1,ωa2,ωa3,…,ωat-1;

3Xj=f(x0,xj);

4Tij=g(Xj)(modn);

5Sij=EXj(Tij);

6Rij=Sij-kij*Nj;//0≤Rij≤Nj

7end

8returnkij,Rij,ω,ωK,ωa1,ωa2,ωa3,…,ωat-1

本文方案利用公开随机数x0和双变量单向函数f(x,y)实现多重秘密的共享且保证了共享的安全性，参与者可利用消息样本ω和公开系统参数ωK,ωa1,ωa2,ωa3,…,ωat-1验证秘密份额的正确性。秘密份额的分发步骤如下所示：

Step1秘密分发者Pd选取安全大素数c1和c2，计算n=c1*c2，选取N1,N2,…,Nn为两两互质的公开正整数，选取公开随机数x0，选取一个消息样本ω。

Step2Pd随机构造一个t-1次多项式g(x)=K+a1x+a2x2+a3x3+…+at-1xt-1，并通过多项式计算ωK,ωa1,ωa2,ωa3,…,ωat-1。

Step3Pd计算用户子集Gi中所有用户的临时密钥Xj=f(x0,xj)。

Step4Pd计算秘密值K对应的用户子集Gi中用户的份额Tij=g(Xj)(modn)。

Step5秘密分发者Pd计算Sij=EXj(Tij)，令Sij=kij*Nj+Rij，其中0≤Rij≤Nj，得到j组(kij,Rij)。

Step6秘密分发者Pd在NB上公开x0,kij,ω,ωK,ωa1,ωa2,ωa3,…,ωat-1。

3.3 基于CRT的身份锁构造

在本文设计中，对于不同的秘密有不同的用户子集{Gi|gi1,gi2,gi3,…,gij}，秘密分发者可根据授权子集构造不同的同余方程组，即根据不同的Nj和Rij构造同余方程。默认用户{U|u1,u2,u3,…,un}和{N|N1,N2,N3,…,Nn}形成一一对应的关系，秘密分发者可根据不同的Rij，kij和x0构造不同的锁X。身份锁用于对当前秘密用户集合进行限制，只有授权子集才能够解开身份锁。

身份锁用于对当前秘密用户集合进行限制，只有授权子集才能够解开身份锁。

身份锁是利用中国剩余定理实现的，秘密分发者先通过算法4得到秘密份额，再利用份额计算秘密对应的身份锁X。秘密分发者只需在公开栏NB上公开锁X，不需要公开份额，有效的参与者通过CRT算法，利用公开的X和自己的基础子份额计算秘密份额。基于CRT的身份锁构造算法如算法5所示。

算法5基于CRT的身份锁构造

Input:N1,N2,…,Nn,Rij,ω,Xj。

Output:X，rj。

1ifP=Pd&&uj∈Gthen

2L=∏Nj;

5rj=EXj(ω);

6end

7returnX和rj

身份锁X限制了恢复不同秘密时，授权的用户子集{Gi|gi1,gi2,gi3,…,gij}不同，利用CRT实现锁X的构造，保证了秘密共享的身份限制。身份锁构造的步骤如下所示：

Step1秘密分发者Pd，对于秘密Si，利用用户Gi中的Nj计算L=∏Nj(j是用户子集Gi中用户所对应的uj)。

Step3秘密分发者Pd根据算法4计算的Rij通过式(2)计算得到X:

(2)

Step4Pd对于消息样本ω，计算Gi中每个用户对应的rj=EXj(ω)。

Step5Pd在NB上公开(X,rj)。

3.4 秘密恢复

所有参与者先通过公开参数验证自己是否为当前秘密的有效参与者，再利用中国剩余定理，根据X和基础子份额计算出自己的份额，并利用公开的参数验证份额的正确性。有效参与者可将自己的秘密份额发送给秘密计算者，当有效参与者达到门限值时，能够恢复秘密。参与者的份额计算算法如算法6所示。

算法6参与者的份额计算

Input:ω,ωK,ωa1,ωa2,ωa3,…,ωat-1,X,x0,xj,rj,Nj,kij(j=1,2,…,n)。

Output:Mj。

1Xj=f(x0,xj);

2ifEXj(ω)=rjthen

3X≡Rij(modNj);

4Sij=kij*Nj+Rij;

5Tij=DXj(Sij);

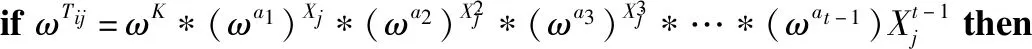
7returntrue;

8end

9end

10returnMj=(Xj,Tij)

参与者计算份额后可通过份额验证来判断份额的真实性，有效的份额参与者可向秘密计算者DC发送自己的有效份额，且秘密的恢复不会影响参与者基础份额的安全性。

秘密计算者DC收到满足阈值的有效份额后，利用拉格朗日插值多项式计算出秘密,如算法7所示。

算法7秘密恢复

Input:Mj。

Output:K。

1ifP=DC&&|Mj|≥tthen

3end

4returnK

当参与者的个数达到t时可以恢复秘密，参与者利用公开参数让用户确定自己是否为秘密的参与者，并通过CRT算法和公开参数计算份额并验证份额的正确性。秘密恢复的步骤如下所示：

Step2参与者uj利用X和Nj计算Rij，满足X≡Rij(modNj)。

Step3参与者uj根据公开的kij，计算Sij=kij*Nj+Rij。

Step4参与者uj利用临时密钥Xj，得到秘密Si的份额Tij=DXj(Sij)。

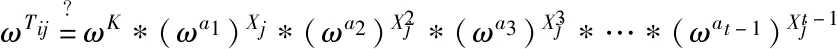
Step6参与者uj将自己的份额Mj=(Xj,Tij)提交给指定的秘密计算者DC(可以是参与者，也可以是其他无关的人)。

Step7秘密计算者DC收到大于或等于t个信息Mj时，可恢复秘密Si。此时Si的计算如式(3)所示：

(3)

3.5 多秘密共享

本文提出的秘密共享方案具有多重秘密共享方案的特性，即只需要每个参与者保存一个秘密份额，该秘密份额可以用于多次秘密共享过程，且秘密份额无需进行更新。

为了提高秘密共享系统的性能，在第1次基础子份额分发之后，秘密分发者和各参与者保存相应的秘密数据x1,x2,x3,…,xn，以便在后续其他秘密共享过程中使用。3.1节～3.4节是单个秘密的分发，如果还需要进一步共享其他秘密，算法可以继续执行以下步骤：

(1)秘密S′i份额分发过程。

秘密分发者Pd不再重新选取秘密数据xj，只需重新选取随机数x′0，并更新此时秘密S′i所对应的用户子集{G′i|g′i1,g′i2,g′i3,…,g′ij}的临时密钥X′j。此时针对不同的秘密多项式构造只需更改K值，在NB上更新ω′K。在3.2节的Step 6中只需在NB上更新x′0,k′ij和ωK′即可。

(2)身份锁更新过程。

秘密分发者不需要再重新选取Nj，只需根据秘密S′i对应的授权子集G′i得到L′，并更新参数f′j,r′j和X′。3.3节的Step 5在NB上更新X′,r′j。

(3)秘密恢复过程。

合作的参与者uj根据更新的X′,x′0和k′ij重新计算X′j和T′ij，在3.4节的Step 5中验证秘密S′i份额的准确性，Step 6和Step 7同3.4节的步骤，且当参与者数量大于或等于t时可以恢复秘密S′i。

重复使用秘密数据x1,x2,x3,…,xn并不会影响共享秘密的安全性，这是由双变量单向函数的性质所决定的，因此本文提出的秘密共享方案具有多重秘密共享方案的特性。

4 分析与证明

4.1 正确性证明

定理1在本文3.1节所述的基础子份额分发方案中，会话密钥的协商中恒有式(4)成立。

e(Qj,sj)e(Sj,Rj)=e(Qj,p)bj

(4)

证明利用参数的构造和双线性变换e运算，可进行如下推导：

e(Qj,sj)e(Sj,Rj)=

e(Qj,bjp-rjSd)e(Sj,rjQd)=

e(Qj,bjp-rjSd)e(Sj,Qd)rj=

e(Qj,bjp-rjSd)e(Qj/P,Sdp)rj=

e(Qj,bjp-rjSd)e(Qj,Sd)rj=

e(Qj,bjp-rjSd)e(Qj,rjSd)=

e(Qj,bjp)=e(Qj,p)bj

□

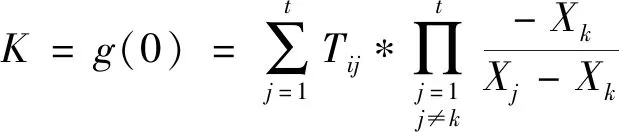
证明从本文方案构造可知，秘密Si存在用户子集{Gi|gi1,gi2,gi3,…,gij}对应的j个点(Xj,Tij)满足g(x)=K+a1x+a2x2+a3x3+…+at-1xt-1的多项式，根据拉格朗日插值多项式的定义可知：

g(x)=K+a1x+a2x2+a3x3+…+at-1xt-1=

因此可得：

K=g(0)=

□

4.2 安全性分析

定理3在基础子份额分发过程中，只有相应的参与者uj(j=1,2,…,n)可以获取秘密分发者发送的秘密数据xj(j=1,2,…,n)，而其他人无法获取该秘密数据。

证明秘密数据xj(j=1,2,…,n)的作用是作为参与者uj(j=1,2,…,n)的基础子份额，其安全性是整个具有身份锁的门限多秘密共享方案安全性的基础。攻击者需要对公告栏上的参数(cj,sj,Rj)进行解密，才能得到秘密数据xj。而公开数据ci需要用会话密钥mj对其进行解密，若要攻破mj等同于攻破对称加密算法，此加密算法的困难性在于椭圆曲线的计算困难以及随机数bj的随机性。因此，除了参与者uj，其他人无法获得秘密数据xj。

□

定理4在多重秘密共享时，参与过秘密恢复的用户uj重用基础子份额xj，不会影响系统的安全性。

证明由定理 3 可知，除了秘密分发者Pd以外，只有参与者uj可以获取基础子份额xj，每个参与者都无法获取其它参与者的基础子份额。本文方案在秘密分发过程中，没有直接使用基础子份额xj进行构造，而是先引入公开随机数x0，再利用双变量单向函数得到伪份额Xj=f(x0,xj)，对不同的秘密Si有不同的公开随机数x0参与运算，具有较高的安全性。在秘密恢复过程中，同样没有直接使用这些秘密信息xj进行恢复，而是使用Xj=f(x0,xj)进行运算。双变量单向函数具有很好的安全性质，尽管每个参与秘密恢复的参与者uj都提供了一个由其基础子份额xj计算得到的伪份额Xj，但根据双变量单向函数的安全性质，该伪份额不会披露其真正的基础子份额xj。

□

定理5在秘密恢复过程中，只有秘密Si相应的用户子集{Gi|gi1,gi2,gi3,…,gij}才可以通过达到门限值的t或t个以上的份额恢复秘密，而其他用户无法恢复该秘密Si。

□

定理6本文具有身份锁的多秘密共享方案符合门限秘密共享方案中的门限规则。

证明在门限秘密共享方案中，先假设此方案的门限为(t,n)，则有2个基本条件必须满足:(1)t或t个以上的参与者合作就可以恢复共享的秘密;(2)(t-1)个或更少的参与者合作无法恢复共享的秘密。对于本文基于身份锁的构造方案而言，也需要满足门限值t，即若要恢复所共享的秘密Si，就必须重新构造出(t-1)次Lagrange插值多项式g(x)。由秘密恢复的过程可知，只有t或t个以上参与者可以计算出满足多项式g(x)的t或t个以上数值对(Xj,Tij)，通过这t或t个以上的数值对，就可以依据定理2重构(t-1)次多项式g(x)，从而计算出共享的秘密Si=K=g(0)。而对于(t-1)个或更少的参与者来说，最多只能提供(t-1)个关于g(x)的数值对。在这种情况下，若要计算出共享的秘密Si，等价于需要攻破Shamir的门限方案，这显然在计算上是不可行的。因此，本文具有身份锁的多秘密共享方案符合门限秘密共享方案中的门限规则。

□

定理7本文方案具备前向保密性，即秘密分发者Pd的私钥泄露不会影响已共享秘密的安全性。

证明前向保密性是指当秘密分发者Pd的私钥Sd不小心或无意中泄露后，已经共享秘密的安全性不会受到任何影响。针对本文方案可知，即使秘密分发者的私钥Sd泄露，秘密分发者通过协商会话密钥mj，发送给各参与者uj的基础子份额xj也不会被任何攻击者所获。因为在秘密Si的公开参数中，cj=Emj(xj‖rj)，Rj=rj*Qd且sj=bj*p-rj*Sd，面对求解离散对数问题，攻击者无法求出bj，则无法得到会话密钥mj，也就无法得到基础子份额xj，而由定理 3和定理4可知，本文方案的安全性主要依赖于参与者uj的基础子份额xj的安全性。因此，秘密分发者私钥Sd的泄露不会对之前所共享的秘密造成安全威胁，即本文方案具备前向保密性。

□

4.3 防欺骗行为分析

在实际通信过程中秘密分发者Pd可能给用户uj(j=1,2,…,n)提供虚假的秘密影子，本文设计的方案可以验证秘密分发者所提供的基础份额和秘密份额是否属实。下面将证明本文方案具有欺骗行为的检测功能。

命题1验证秘密分发者提供的基础份额是否属实。

□

命题2验证秘密分发者提供的秘密份额是否属实。

□

4.4 性能分析

本文提出的具有身份锁的门限多秘密共享方案结合了CRT的身份锁控制算法，避免了现有秘密共享方案中，不同秘密的访问控制结构可能相同的缺点。表2给出了本文方案和其他方案的性能比较情况。

从表2可以看出，在这些秘密共享方案中：

(1)只有本文方案提供了恢复秘密时对参与者的身份控制，对于不同的秘密,由不同的用户子集来参与运算恢复秘密，具有更好的应用价值，可用于电话会议和文件分发等应用场景。

(2)本文对不同的秘密Si，引入rj=hmj(xj)来验证参与者身份，减少了用户盲目计算的情况，而文献[7-9]都是利用NB来公布有效的参与用户，这种做法会引来恶意敌手的主动攻击。

(3)在秘密份额重用方面，本文方案与文献[8,9]提出的方案达到一样的效果，每个参与者的秘密份额可以用于多次秘密共享过程而无需更新；文献[7]的方案在每次秘密共享过程前，都需要重新分发秘密份额，通信量较大。

(4)在安全信道方面，本文方案使用会话密钥的协商方案，用会话密钥对秘密数据进行保护，不需要安全信道；而在文献[7]提出的方案中，预设了安全通道，且后期需维护安全信道，以保证方案的安全性。

(5)本文可以提供参与者对秘密分发者分发份额的验证功能，可以预防分发者可能出现的各种欺骗，增强了系统的安全性，也减少了参与者无效的计算。文献[7-9]也提供了对秘密分发者和参与者的验证，保证了方案可有效检测欺骗行为。本文中参与者是利用公开参数检测份额进行验证，确保了方案的实用性和正确性。

(6)在安全性方面，文献[7]提出的方案通过安全信道进行秘密份额的分发，秘密分发者私钥的泄露必将影响秘密份额的安全性，从而也影响共享秘密的安全性。而本文方案基于协商密钥的方案具有前向保密性；且本文引入椭圆曲线计算，保证了会话密钥的安全性，从而保证了秘密数据的安全性。通过分析可知，本文方案更有效，也更符合实际应用。

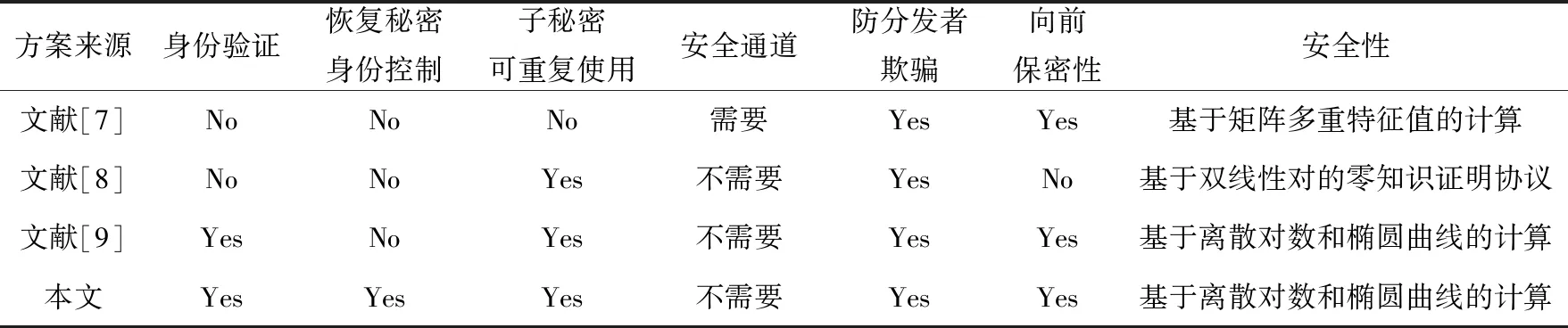
Table 2 Performance analysis表2 性能分析

5 结束语

本文提出了一种具有身份锁的门限多秘密共享方案，针对不同秘密，基于CRT的身份锁控制算法构造不同的安全锁，实现秘密份额只能由对应用户集合中的用户打开，而系统中的其他用户无法打开，且不同的秘密会存在不同的安全锁。同时，本文方案子秘密还可重复使用，且可检测秘密分发者欺骗行为，也不需要通过安全通道来传输秘密份额，具有很好的安全性和实用性。本文的方案可应用于门限秘密共享更复杂的场景。未来将在本文方案的基础上，考虑如何进行参与者的欺骗检测和抵抗参与者的恶意攻击。