基于LSTM的集群用户作业执行时间预测模型*

朱正东，吴寅超，胡亚红，蒋家强

(1.西安交通大学计算机学院，陕西 西安 710049;2.浙江工业大学计算机科学与技术学院，浙江 杭州 310023)

1 引言

进行有效的作业调度可以保证数据中心在指定的截止时间前完成用户作业，从而提高用户满意度。作业调度是NP-hard问题，一直是分布式系统中的研究热点。预知作业的执行时间是开始作业调度的前提。根据各用户作业的预测执行时间和截止时间，数据中心可以进行有效的任务调度和资源分配，从而缩短用户作业的完成时间，提高系统性能。

目前预测用户作业执行时间的常用方法是先运行少量用户作业，得到作业执行时间，再根据这个时间预测完整的用户作业的执行时间[2]。这种方法的不足之处有2点：一是作业的完成时间和作业量之间通常不是简单的线性关系；二是若用户作业的数据量巨大、整体耗时较长，简单地按照固定的系统资源量进行预测，不考虑节点实时性能的变化，会导致时间预测精确不高。因此,很有必要对用户作业执行时间的预测模型进行深入研究。

用户作业执行时间预测属于时间序列分析领域。传统的时间序列分析采用线性模型，如整合滑动平均自回归ARIMA(AutoRegressive Integrated Moving Average)模型[3,4]。线性模型简单易用，但是预测精度不高。为处理各种复杂应用场景，非线性模型分析方法不断出现，如人工神经网络ANN(Artificial Neural Network)[5]、支持向量回归SVR(Support Vector Regression)[6]和长短期记忆LSTM(Long Short-Term Memory)网络[7]等。LSTM是一种时间循环神经网络，在交通管理、电力系统管理、状态监测、金融风险管理及行情预测等领域都应用广泛。

LSTM在交通数据的分析中取得了不少成果。因为需要准确地统计交通流热力分布比对，同时对交通数据进行预测分析，以判定交通资源调配是否合理，叶奕等[8]提出了基于Hadoop平台及LSTM 网络的城市交通出行数据挖掘模型，以保证交通系统的健康发展。

准确预测公交车的到站时间和客流量有助于进行合理的调度规划，从而缓解交通拥堵、方便公众出行。基于历史数据的预测对于短期预测反应较慢，而基于车辆实时速度的时间预测又无法得到较长时间的预测结果。针对该问题，Liu等[9]提出了一种基于时空特征向量的长短期记忆和人工神经网络的综合预测模型。该模型从时间特征的维度实现了远距离车辆到站时间预测，从空间特征的维度实现了短距离车辆的到站时间预测。李高盛等[10]提出的基于LSTM的城市公交车站短时客流量预测算法，能够找出公交站点之间潜在的相关性，并具有一定的泛化能力。

为加强能耗数据的管控、合理优化资源配置、科学地提高水电能源使用效率，赵金超[11]提出了基于LSTM的能耗数据分析混合模型——经验模态分解-长短期记忆网络-差分自回归移动平均EMD-LSTM-ARIMA(Empirical Mode Decomposition- LSTM-AutoRegressive Integrated Moving Average)模型。该模型分别对分量序列进行预测，再对各分量的预测结果等权值求和，能够得到较为准确的预测结果。庄家懿等[12]为了解决输入数据特征量受限时短期电力负荷预测精度较低的问题，提出了基于多模型耦合的卷积神经网络-长短期记忆网络-极端梯度增强算法CNN-LSTM-XGBoost(Convolutional Neural Network-LSTM-eXtreme Gradient Boosting)预测方法。为了保障电网的有效调度和电力系统的稳定运行，需要准确地对光伏电站的辐射强度进行预测。与其他模型相比，邱瑞东等[13]提出的基于长短期记忆网络-轻度梯度提升LSTM-LGB(LSTM-Light Gradient Boosting)的辐射强度预测方法能够提供较高的预测准确度。马磊等[14]将Attention机制与LSTM网络相结合建立的预测模型，通过Attention机制为LSTM的输入特征赋予不同的权重，从而使得预测模型对长时间序列输入的处理更为有效。这个模型应用于超短期光伏发电功率预测时，能够提高电网的调度管理水平和电力系统运行效率。

与传统的维修方式相比，基于故障监测的预知维修可以有效地防止机械设备的突发性故障，减少维修成本。郭旭东等[15]提出使用CNN-LSTM模型进行机电设备的剩余使用寿命预测，以最大限度地利用装备的工作能力。康玄烨等[16]使用LSTM构建故障数量的预测模型，通过挖掘补偿电容故障数量随时间的变化规律，实现了对补偿电容未来一段时间内故障数量的预测。该预测结果能够对管理部门提前准备维修所需的资金、人员和设备起到指导作用。申彦斌等[17]使用双向LSTM挖掘轴承在实际工作过程中的退化规律，完成了对轴承剩余使用寿命的预测。针对处于传感器报警阈值以下的工业生产装置的故障难以及时捕捉的问题，窦珊等[18]引入了基于LSTM的模型来估计发生异常的概率，完成了对时间序列的异常检测。

在金融领域，LSTM用于行情预测和信誉度预测等，能够帮助企业和个人规避风险。对信用债个体违约风险进行及时跟踪和预测，对于我国债券市场的稳定与健康发展具有重要意义。因此，陈学彬等[19]使用LSTM构建了中国信用债违约风险预测模型，其预测结果与国内权威的评级结果非常接近。彭燕等[20]提出的基于LSTM的股票价格预测模型，可以帮助投资者了解股票走势，建立合适的投资策略。影响电煤价格的因素众多且非线性强，廖志伟等[21]提出了基于LSTM的中短期电煤价格预测模型。

近年来，LSTM在分布式系统资源管理方面也有许多研究成果。降低功耗能够有效地减少集群的运行成本，为此，韩庆亮[22]提出了一套Hadoop集群节能系统方案，该方案包含一个基于节点负载状态预测的任务调度算法——Hadoop能源节省调度器HES-Scheduler (Hadoop Energy Saving Scheduler)。通过使用节点的历史负载数据对LSTM模型进行训练，能够预测节点在未来周期的负载情况。调度算法让预测负载较低的节点进入休眠，以降低集群的能耗。为了提高数据中心服务质量，需要降低系统故障带来的损失,Gao等[23]提出使用多层双向LSTM分析系统的历史数据，能够更加准确地预测出系统故障的发生。

系统资源使用情况预测是进行实时任务调度的关键。Ruan等[24]提出了基于深度学习的存储负载预测模型CrystalLP。该模型包含负载采集、数据预处理、时间序列预测和数据后处理等阶段，其中时间序列预测采用了LSTM。针对集群资源实时变化性强的特点，Gupta等[25]建立了一个稀疏框架以完成快速的资源使用情况预测。为解决用户过度申请资源而导致数据中心整体资源使用率下降的问题，Thonglek等[26]提出了基于LSTM的作业最优资源分配算法。

目前，使用LSTM进行用户作业执行时间预测的研究较少。本文设计和构建了基于LSTM作业执行时间预测模型的作业调度算法，以缩短用户作业的完成时间，提高数据中心的服务质量。本文还分析了时间预测模型的输入，进行了预测模型结构设计，并详细介绍了模型中各超参数的确定方法。实验表明，本文模型的预测误差较小，能够满足工程应用要求。

2 基于作业执行时间预测的作业调度算法

预测用户作业的执行时间，不但可以确定数据中心是否有能力在用户规定的时间内完成作业，还为进行合理的作业调度提供了依据。基于时间预测的作业调度算法如图1所示。图1中jb是批作业中的作业数量，Uremain表示数据中心剩余资源占总资源量的比例，初始值为1。当系统剩余资源可以满足某作业的资源需求且能保证其在截止时间前完成时，可以将这个作业与其它作业并行执行。作业执行并行度的提高有助于缩短批作业的完成时间，提升数据中心的资源利用率。

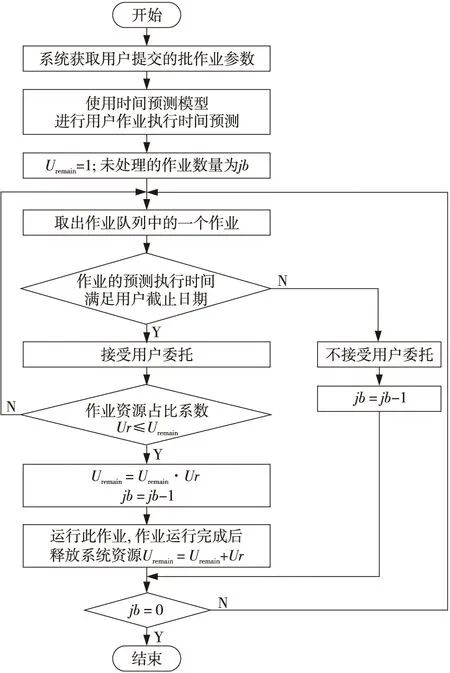
Figure 1 Flowchart of the job scheduling algorithm based on the execution time prediction model图1 基于作业执行时间预测的作业调度算法流程图

图1中Ur表示作业的资源占比系数，表示用户所需要的资源量占数据中心资源总量的比例，其计算如式(1)所示：

(1)

对于每一个作业，数据中心首先对其进行执行时间预测。当发现作业预计的执行时间不能满足用户的作业截止时间要求时，则及时告知用户，由用户自行决定是延长截止时间还是转去其它数据中心。当数据中心为一个作业进行资源分配后仍有资源可用时，则继续选择满足资源要求和截止时间要求的作业与当前任务并行执行。此算法的基本思想是利用预测的作业执行时间，判断是否能够为用户提供高质量的服务，同时尽可能提高作业执行的并行度，以缩短批作业的完成时间。

作业执行时间预测模型是本文算法的核心，下面将详细介绍基于LSTM的作业执行时间预测模型的结构和构建方法。

3 基于LSTM的作业执行时间预测模型的构建

3.1 LSTM神经网络

神经网络包括输入层、隐藏层和输出层，输出控制主要由激活函数进行调整，每2层之间都存在权值连接。普通的神经网络没有考虑输入样本之间的关联，样本的处理在各个时刻相互独立，每层神经元的信号只能向上一层传播。循环神经网络RNN(Recurrent Neural Network)是一种特殊的神经网络，可以看成是一个在时间上传递的神经网络，这使得神经网络对前面输入的内容具有了记忆功能，因而适合处理时间序列问题。

但是，由于存在梯度消失和梯度爆炸问题，RNN无法有效处理长序列数据。长短期记忆LSTM网络就是为了解决这一问题而提出的改进算法。LSTM使用门控结构来控制长期状态信息[27]，其细胞结构如图2所示，其中Ct是t时刻的细胞状态，ht是t时刻的隐藏状态。

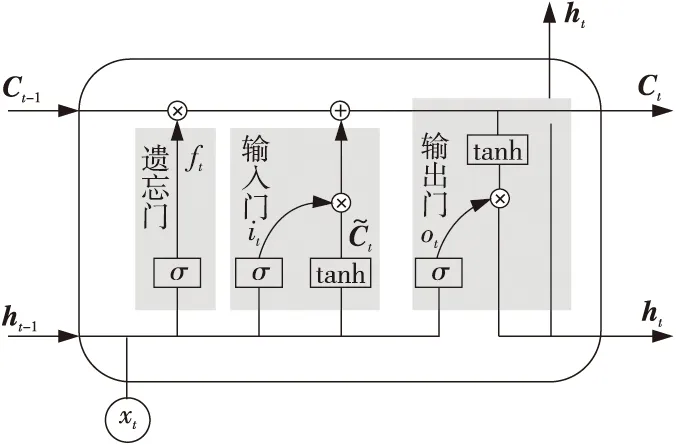
Figure 2 Cell structure of LSTM 图2 LSTM细胞结构图

LSTM中所采用的门控结构主要包含如下3种：

(1)遗忘门(Forget Gate)。

假设当前时刻为t,LSTM神经网络中遗忘门决定了如何对t-1时刻的细胞状态Ct-1进行保留和舍弃。遗忘门的输出ft通过式(2)计算得到：

ft=σ(Wf·[ht-1,xt]+bf)

(2)

其中,σ(·)是sigmoid激活函数，Wf和bf分别为遗忘权重和偏置矩阵，xt是t时刻的输入，ht-1是t-1时刻的隐藏状态。ft=1表示t-1时刻的细胞状态Ct-1被完全保留，ft=0则表示Ct-1被全部舍弃。

(2)输入门(Input Gate)。

输入门的主要功能是处理当前时刻t的输入，它由2部分组成。第1部分采用了激活函数sigmoid，输出it,其计算如式(3)所示：

it=σ(Wi·[ht-1,xt]+bi)

(3)

其中Wi和bi分别为输入权重和偏置矩阵。

(4)

其中WC和bC分别为对应的权重和偏置矩阵。

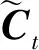
(5)

(3)输出门(Output Gate)。

隐藏状态ht的更新由2部分组成:第1部分是ot,它由t-1时刻的隐藏状态ht-1和t时刻的输入数据xt，以及sigmoid激活函数计算得到;第2部分由Ct和tanh激活函数计算得到,分别如式(6)和式(7)所示：

ot=σ(Wo·[ht-1,xt]+bo)

(6)

ht=ot*tanh (Ct)

(7)

其中Wo和bo分别为输出权重和偏置矩阵。

通过遗忘门、输入门和输出门的控制，可以得到当前时刻t的细胞状态Ct和隐藏状态ht。

3.2 模型的输入和输出

用户提交作业时，一般会给出作业的数据量、对数据中心资源的需求量和作业期望的完成时间等信息，基于LSTM的用户作业执行时间预测模型将根据这些输入，完成作业执行时间的预测。影响用户作业执行时间的因素很多。从作业的角度，在相同的系统配置下，同样类型的作业，其数据量越大，完成的时间会越长；而同样数据量、不同类型作业的运行时间则会有所不同[28]。从系统资源的角度，CPU核数、CPU负载、内存量和网络带宽等都会影响作业的执行时间[29]。本文选取如下5个影响因素作为执行时间预测模型的输入：

(1)作业类型：一般可分为CPU密集型、内存密集型和网络密集型等。

(2)用户作业所需CPU数量：用户提交作业时要求的CPU核数。

(3)用户作业所需内存量：用户提交作业时要求的内存数量。

(4)用户作业的数据量大小：需要用户提交，对作业的执行时间有较大的影响。

(5)作业的资源占比系数：用户所需要的资源量占数据中心资源总量的比例，通过式(1)计算得到。

预测模型通过发掘各个因素之间的隐性关系，完成作业执行时间的预测。

3.3 模型结构

基于LSTM的用户作业执行时间预测模型如图3所示。模型的输入为用户作业的参数，输出为预测的作业执行时间。LSTM在每一个时刻的输入向量xt的维度为5，即影响作业执行时间的5个影响因素——作业类型、用户作业所需CPU数量、用户作业所需内存量、用户作业的数据量和作业资源占比系数。Ct和ht对应的向量维数为隐藏层神经元的个数。LSTM的输出h由对应的细胞状态Ct和tanh激活函数，通过式(7)计算得到。隐藏层的层数和隐藏层神经元的个数通过实验确定。最后一个隐藏层的输出通过全连接层FC (Fully Connected layer)与输出向量连接。

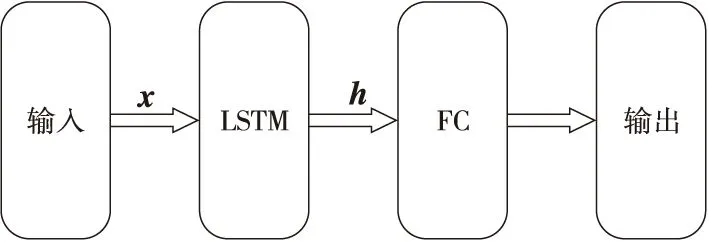
Figure 3 Structure of the user job execution time prediction model based on LSTM图3 基于LSTM的用户作业执行时间预测模型结构

本文所采用的损失函数为均方差MSE(Mean Square Error)，其计算方法如式(8)所示：

(8)

3.4 模型评价指标

用户作业执行时间预测属于回归问题，常用的评价指标有均方根误差、平均绝对误差、平均绝对值百分比误差和决定系数等。

(1)均方根误差RMSE(Root Mean Square Error)。

与MSE相比，RMSE可以降低误差的级别，RMSE的值越小，意味着预测模型越有意义,其计算如式(9)所示：

(9)

(2)平均绝对误差MAE(Mean Absolute Error)。

MAE的单位和RMSE是一样的，其计算方式如式(10)所示：

(10)

(3)平均绝对值百分比误差MAPE(Mean Absolute Percentage Error)。

平均绝对值百分比误差的取值在[0,+∞)，通过式(11)计算得到，其值越小表示模型越精确。

(11)

(4)决定系数R2(Coefficient of Determination)。

决定系数也称作拟合优度，通常用来衡量模型能否很好地描述真实数据的变化，其计算如式(12)所示：

(12)

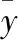
3.5 超参数调优

LSTM模型中超参数的取值对预测结果的准确性有非常大的影响，所以在正式训练模型之前，本文通过实验确定超参数最佳取值。影响LSTM模型的超参数包括学习率、迭代次数、网络层数、隐藏层节点数和Dropout率等，下面逐一进行分析。

3.5.1 学习率和迭代次数

学习率lr(learning rate)在迭代过程中用来决定网络梯度更新的幅度，其经典取值在0.1～0.000 001。学习率的取值过大，容易导致最终结果在最优处反复震荡，无法收敛；取值过小，则整个网络的训练速度会变得很慢。

本文进行lr调优的方法是首先使用迭代过程中对应的损失值来确定学习率的量级，再通过微调确定最佳学习率。不同学习率对应的损失函数值如图4所示。

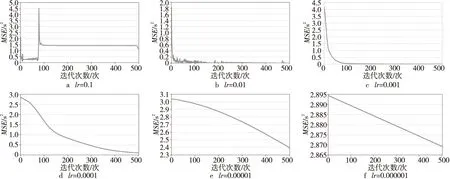
Figure 4 Loss function curves corresponding to different learning rates图4 不同学习率对应的损失函数曲线

从图4可以发现，学习率为0.1时，学习率过大，在迭代次数较少的时候发生了振荡的现象,而增加迭代次数后，虽然产生了收敛的趋势，但是收敛对应的误差非常大，仍然无法满足模型的精度要求。当学习率取值为0.000 1，0.000 01和0.000 001时，在500次迭代次数之内，误差曲线处于未收敛状态，此时模型是欠拟合的。将迭代次数调整到1 000次以上时，3种学习率对应的损失值曲线呈现收敛状态，但是误差较大，还是无法满足精度要求，且迭代次数超过1 500次后时间成本大幅上升。在学习率取0.01和0.001时，损失函数的曲线呈现正常收敛状态，但学习率为0.01时，对应的损失曲线在收敛时有些许波动幅度，不如学习率为0.001时的曲线平滑。经过验证和微调后，本文最终将学习率取值为0.006。

进行LSTM模型训练时，过少的迭代次数会产生较大的误差，无法让模型达到预期的效果。本文为了找到合适的迭代次数，在确定学习率之后，对LSTM模型进行了多次训练，不同迭代次数对应的误差如图5所示。

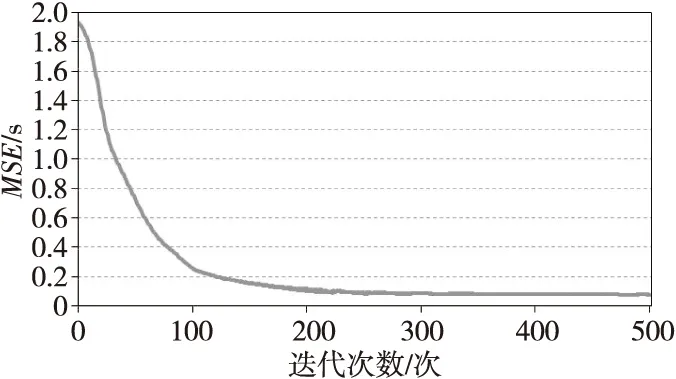
Figure 5 Error curve corresponding to different number of iterations图5 不同迭代次数对应的误差曲线

从图5可以发现，在迭代数次增加到300次之后，误差曲线开始趋于平缓，呈收敛态势。本文结合所构建的网络模型和数据量，确定迭代次数为500次即可使模型的预测精度达到预期要求。

3.5.2 网络层数

Chen等[30]指出，增加LSTM网络隐藏层数有利于提升模型预测精度。但彭燕等[20]通过实验发现，一味增加层数并不能一直增加模型精度，往往只是增加了训练的复杂度。本文综合考虑时间成本和期望模型的复杂度，选取了2～3层的网络进行实验，通过对比实验的结果来进一步确定网络层数。实验结果如图6所示。

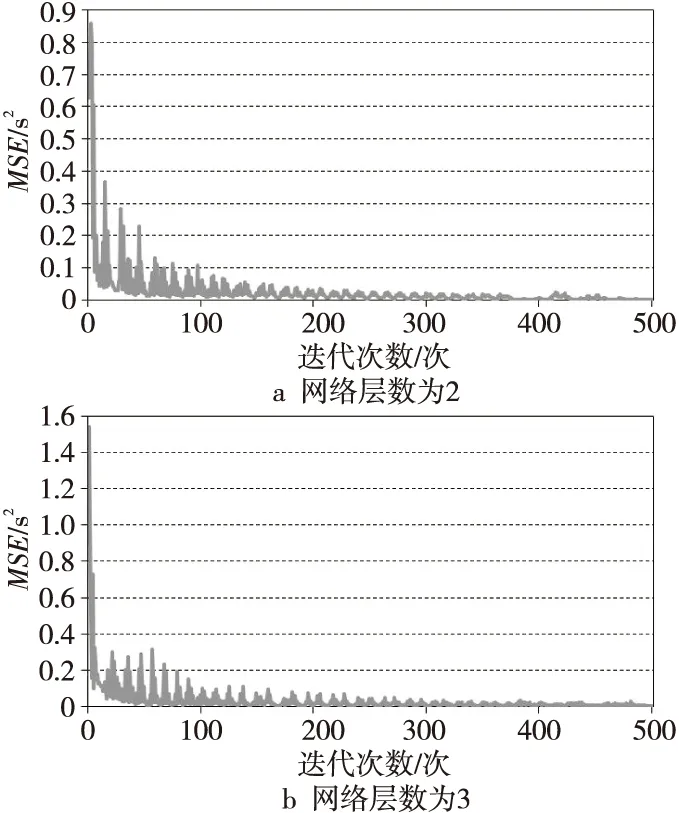
Figure 6 Error curves corresponding to two- and three- layer network 图6 不同网络层数对应的误差曲线

从图6可以发现，分别以2和3作为网络层数建立的模型，两者对应的误差曲线都在迭代300次左右开始收敛。相比于3层网络，2层网络在迭代次数较小时的误差较小，且在趋向收敛时其均方根误差更小，模型精度更高，因此本文模型中的网络层数取2。

3.5.3 隐藏层节点数和Dropout率

隐藏层节点可以使网络模型学习数据之间隐藏的关联。若隐藏层节点数过少，会导致模型无法充分发掘数据之间的隐性关系，导致预测效果差；若隐藏层节点数过多，则容易发生过拟合现象，即使没有过拟合，也会使网络变得过于复杂，增加训练时间。夏克文等[31]通过研究得到了确定最佳隐藏层节点数的经验公式，如式(13)和式(14)所示：

(13)

(14)

其中,nh,ni和no分别代表神经网络的隐藏层节点数、输入层节点数和输出层的节点数，m是取值为 [1，10] 的常数。根据这2个公式和隐藏层节点优化搜索算法可以确定最佳隐藏层节点数，具体步骤如下：

步骤1因为本文的ni=5，no=1，根据式(14)可得，a=3，b=16，所以隐藏层节点数的取值在[3,16]。通过黄金分割比例公式计算得到第1个实验点e1=0.618*(b-a)+a=11。

步骤2计算第2个实验点e2=0.382*(b-a)+a=7，通过实验得到隐藏层节点数为11时对应的RMSE值为12.35，小于隐藏层节点数为7时对应的RMSE值13.83。根据文献[31]中提出的黄金分割舍劣取优的方式，由于11对应的误差更小，所以留下11所在的优势区间，舍弃掉7所在的劣势区间[3,7)。这样可将区间进一步缩小为[7,16]。

步骤3利用黄金分割法求得拓展区间为[16,24]。因为16=0.618*(c-a)+a且a=3，所以c=24。如此，可得到拓展取值在[7,24]。

步骤4在[7,24]中反复实验，得到的各个隐藏层节点数对应的RMSE值如表1所示。其中RMSE相对最小的隐藏层节点数为15，19，21和22。

Table 1 RMSE corresponding to the node number of the hidden layers表1 各个隐藏层节点数对应的RMSE

在得到相对较优的隐藏层节点数之后，再根据模型的多个评价指标值选取最优节点数，对比情况如表2所示。

Table 2 Evaluation index values corresponding to different hidden node numbers表2 不同隐藏节点数所对应模型的评价指标值

从表2可以看到,当隐藏层节点数为21时，其RMSE、MAE和R23个评价指标的值都是最优的,其MAPE值也低于节点数为15和19时的情况，仅比最低值高了3.00%。本文综合考虑网络的复杂程度和计算成本，将网络模型的隐藏层节点数确定为21。

合适的Dropout率可以有效地降低过拟合现象发生的概率，起到一个正则化的作用。通常Dropout率的取值在0.1～0.3，本文通过实验确定Dropout率的取值，实验结果如表3所示。从表3可以看出，当Dropout率为0.1时，模型各项评价指标的取值可以达到较为理想的状态，因此本文模型的Dropout率设为0.1。

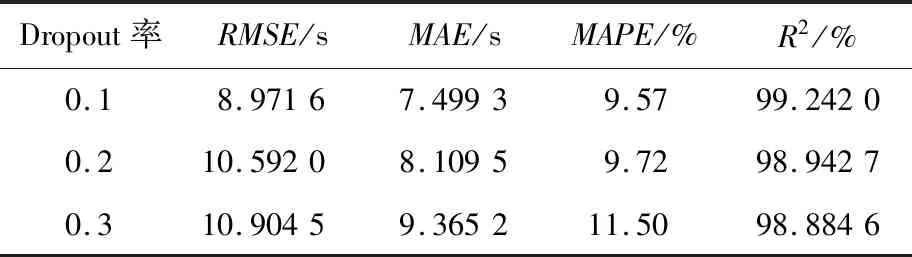
Table 3 Model errors corresponding to different dropout rates表3 不同DropOut率对应的误差

3.6 模型训练

在确定了基于LSTM的用户作业执行时间预测模型的超参数后，本文开始模型训练。本文所有进行时间预测模型训练和测试的数据采集于表4所示的Spark集群。

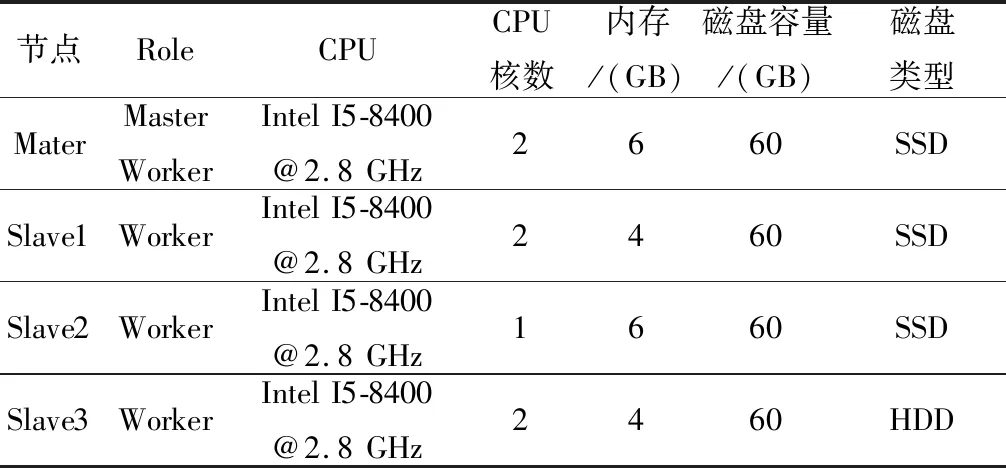
Table 4 Data collection cluster configuration表4 数据采集系统配置表

根据用户作业类型对采集的历史数据进行分类，可分为CPU密集型、内存密集型和默认不定义类型等。将CPU密集型数据集记为DCPU={cp1,cp2,…,cpn}，内存密集型数据集记为DMem={me1,me2,…,mem}，默认不定义类型数据集记为Ddefault={de1,de2,…,des}，则历史数据集可以表示为D=DCPU∪DMem∪Ddefault。每一条数据都包含作业类型、CPU数量、内存数量、作业数据量和资源占比系数5个影响因素和作业的实际运行时间。本文共采集数据400条，其中150条是WordCount负载对应的数据，150条是Sort负载对应的数据，其余100条属于Ddefault集合。

对D中的数据使用Max-Min法进行归一化处理，并按照80%和20%的比例划分成为训练集Dtrain和测试集Dtest。

4 实验及结果分析

为了检验基于LSTM的用户作业执行时间预测模型的有效性，本节分别对WordCount和Sort 2类工作负载进行了数据采集和运行时间预测。

4.1 实验环境

训练模型所采用的超参数取值如表5所示。

Table 5 Values of the hyper-parameters表5 模型超参数取值

时间预测模型的软硬件运行环境如表6所示。

Table 6 Software and hardware configuration for the experiments表6 实验软硬件配置

4.2 实验结果

为了考察时间预测模型的准确性，实验环节没有采用进行模型训练的数据集。新的数据集同样在表4所示的集群上运行产生，分别为24组WordCount作业和24组Sort作业。在得到作业的实际运行时间后再使用时间预测模型对这些作业进行运行时间预测，得到各作业的预测执行时间。

将LSTM模型的预测结果和经典的BP神经网络模型、ARIMA线性模型和SVR模型的进行对比。所有模型均运行在表6所示的环境中。BP神经网络的参数设置如下：5个输入参数，1个输出参数，2层隐藏层，隐藏层节点数为21，Dropout率为0.1，使用sigmoid作为激活函数。ARIMA模型的参数 (p,d,q)取值为(3,1,1)。SVR模型中的参数取值分别为：惩罚系数C=104，kernel为sigmoid，gamma='auto'，coef0=0.0，tol=10-4，最大迭代次数max_iter=1000，其余参数使用默认值。

使用这4种模型对用户提交的作业进行执行时间预测，得到的模型评价指标值如表7所示。

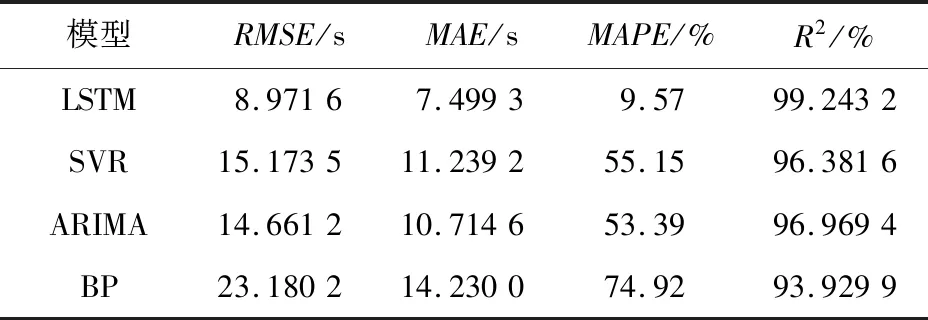
Table 7 Corresponding evaluation index values of different models表7 不同模型对应的评价指标

由表7可知，LSTM模型的各项指标所显示的误差都较小，拟合优度R2是最高的。相对于SVR模型、ARIMA模型和BP模型，LSTM模型在R2上分别有2.97%,2.34%和5.66%的提升效果，这意味着LSTM模型可以较为精准地预测用户作业的执行时间。

为了进一步对LSTM时间预测模型的可用性进行分析，本文将预测结果和作业真实执行时间进行了对比，结果如图7和图8所示。图7呈现的是作业真实执行时间与LSTM模型给出的预测时间对比，图8给出了每个作业预测时间的误差及误差的平均值。

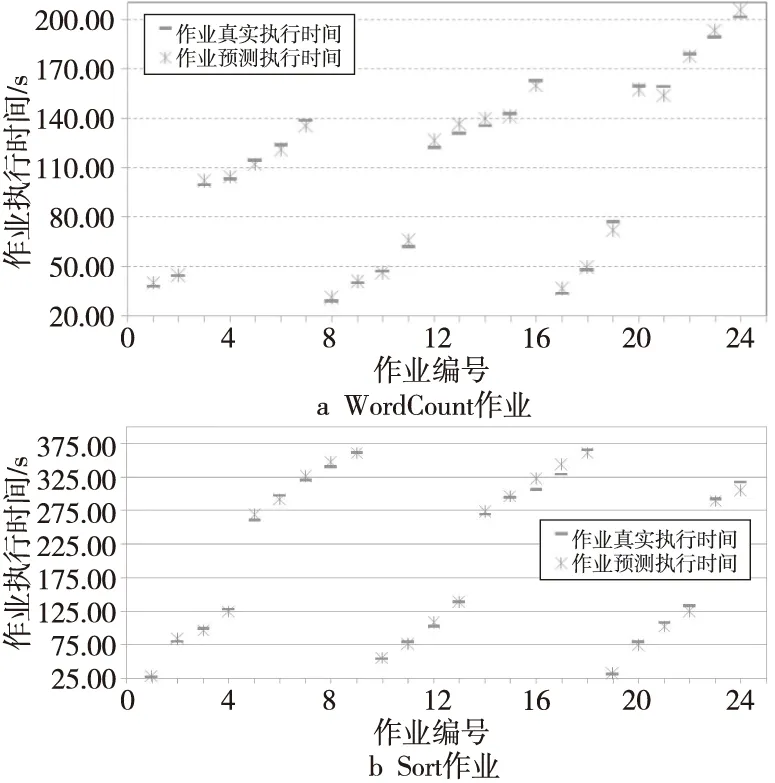
Figure 7 Comparison of jobs’ running time and prediction time of LSTM model图7 作业真实执行时间与LSTM模型预测时间对比

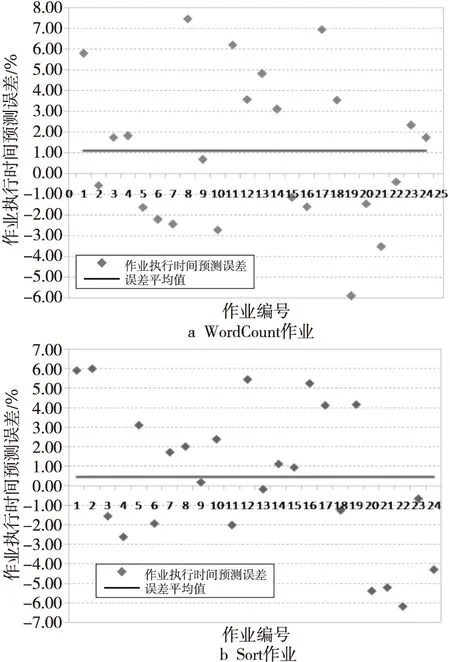
Figure 8 Error of LSTM based time prediction model图8 LSTM模型作业执行时间预测误差

可以看出，由LSTM模型预测得到的作业执行时间和真实的用户作业执行时间非常相近，平均误差为0.78%。对WordCount作业的预测误差为1.0972%±3.5031%；对Sort作业的预测误差更小，但是标准差略大，为0.4667%±3.6076%。预测的误差时间高于或低于真实作业运行时间对作业调度有不同的影响。预测时间低于真实执行值可能导致无法按时成完用户作业；反之，则会导致集群拒绝有能力按时完成的作业。具体的误差分析结果如表8所示。

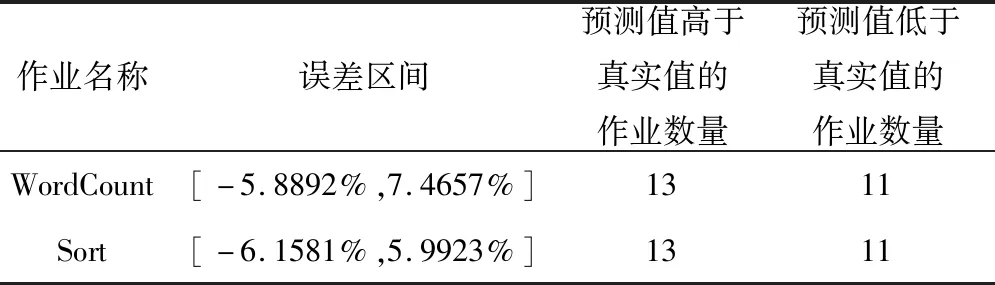
Table 8 Error analysis of experimental results表8 实验结果误差分析

从表8可知，正误差和负误差的数量相当，且都不超过10%。假设预测的作业执行时间为y小时，满足用户要求的作业运行时间为z小时。当z≤1.1y，就可以确定集群能够为用户提供服务，保证了用户满意度。

5 结束语

为了提高数据中心的服务质量，数据中心必须保证在用户要求的截止时间前完成作业。因此，在接收用户作业前，数据中心需要根据当前可用资源预测出作业的完成时间，以确定是否能够为用户提供服务。本文提出了一种基于LSTM的用户作业执行时间预测模型，在描述了模型所需的输入、输出后，通过实验和分析确定了LSTM模型所需的超参数取值，以提升模型的效率和精度。实验表明时间预测模型的拟合优度R2能够达到99.24%，平均预测误差为0.78%，优于对比组的时间预测模型。

目前本文所使用的历史作业数据量较少，考虑的作业类型也较少，为了进一步提升模型的预测精度，下一步将继续增大训练数据规模；单一模型的预测效果通常没有复合模型好，下一步将把LSTM与注意力机制相结合，提出性能更好的模型；同时将在真实数据中心上进行更多的实验来验证模型的有效性和可扩展性。