改进残差神经网络实现心音分类*

张俊飞,张贵英

(1.广州医科大学信息与现代教育技术中心,广东 广州 511436;2.广州医科大学基础医学院,广东 广州 511436)

1 引言

心音信号是由心肌收缩、心脏瓣膜开闭和血液流动撞击等引起的振动所产生的声音。心音信号包含大量心脏生理信息，心音检测结果可以比其他检测结果更早表现器质性心脏病体征[1]，因此对心音信号的有效分析有助于心脏疾病无创诊断。

当前深度学习在心音分类领域已经得到大量的应用。根据当前心音分类领域深度学习神经网络模型组合方式和训练方法，深度学习应用在心音分类领域的模式可分为以下3种：(1)一种或多种神经网络模型组合。许春冬等[2]通过构造心音功率谱密度特征矩阵，利用卷积神经网络实现心音分类，基于2016年PhysioNet/CinC挑战赛(简称CinC2016)数据的分类准确率、灵敏度和特异度分别为84.72%,77.63%和94.63%。李伟等[3]结合卷积神经网络和循环神经网络分别提取心音的频域和时域特征进行训练，基于CinC2016数据的分类准确率为85.70%。Noman等[4]基于心音原生数据和梅尔频率倒谱系数MFCC(Mel-Frequency Cepstrum Coefficient)特征利用一维卷积和二维卷积神经网络进行心音二分类，基于CinC2016数据的分类准确率、灵敏度和特异度分别为89.22%,89.94%和86.35%。Li等[5]将传统的特征工程方法与设计的卷积神经网络相结合，对心音进行自动分类，基于CinC2016数据的分类准确率、灵敏度和特异度分别为86.80%,87.00%和86.60%。Zabihi等[6]从原生心音数据的时间、频率和时频域维度提取特征，利用前馈神经网络进行分类，基于CinC2016数据的分类平均准确率、灵敏度和特异度分别为85.90%、86.91%和84.90%。(2)机器学习和神经网络模型组合。Potes等[7]从原生心音数据124个时频特征和4个频带特征2个维度，分别应用AdaBoost分类器和一维卷积神经网络进行训练，最后结合决策，其基于CinC2016数据的分类平均准确率、灵敏度和特异度分别为86.02%,94.24%和77.81%。韩威等[8]改进文献[7]分类模型中的一维卷积为二维卷积，其准确率、灵敏度和特异度分别为91.08%±1.79%,93.03%±3.12%和89.14%±1.92%。(3)辅助模块参与的深度学习心音分类。Chen等[9]参照ECG信号利用隐马尔可夫模型寻找心音信号中S1、S2、收缩期和舒张期确切位置，再进行心音分段并输入到卷积神经网络中，基于CinC2016数据的分类平均准确率、灵敏度和特异度分别为94.00%,95.00%和93.00%。Han等[10]首先对心音数据进行分段并提取每段MFCC特征，再在神经网络模型中引入辅助阈值映射心音段类别到心音实例类别，基于CinC2016数据的分类平均准确率、灵敏度和特异度分别为91.50%,98.33%和84.67%。

深度学习摒弃了传统机器学习的特征工程环节，为心音分类提供了简单便捷的端到端模式，因此特征工程方式、机器学习与深度学习组合使得心音特征获取、网络模型结构过于复杂；辅助模块的参与明显提升了心音分类的准确度，但是辅助模块需要更多的运算，也使模型变得复杂，偏离了深度学习理念。秉承特征获取简易、网络模式简单和分类准确率高的需求，本文利用ResNet152模型对CinC2016数据进行深度学习，应用CBAM(Convolutional Block Attention Module)注意力机制到心音特征提取中，使得特征更加有效；利用Focal Loss损失函数缓解心音数据不均衡带来的分类不准确问题，同时有利于心音难例分析；利用多尺度心音特征使得心音信号表达更加准确。

2 数据预处理

2.1 数据介绍

本文采用2016年PhysioNet/CinC挑战赛中的比赛数据。该数据共由6个数据库(A～F)组成，总计3 240个心音记录，其中正常心音2 575个、异常心音665个。

2.2 数据重采样

心音数据重采样的目的是保留有效心脏活动声音信号，减少数据量和后期运算时间。正常心音频率一般在50 Hz到800 Hz[11]，根据奈奎斯特采样定理，本文采用2 000 Hz采样频率完整保留原始信号有效信息。

2.3 数据去噪

对于正常心音频率区域外的高频、低频噪音信号，先由5阶巴特沃斯带通滤波器去噪；对于区域内的噪音信号，采用小波阈值去噪。

5阶巴特沃斯带通滤波频带设为50～800 Hz，由其频率响应(图1)可知，基本保留了0.05～0.8 kHz区间信号。图2展示了一条心音信号滤波前后频谱对比，滤波后的心音数据在50 Hz之前和800 Hz之后均有所衰减。

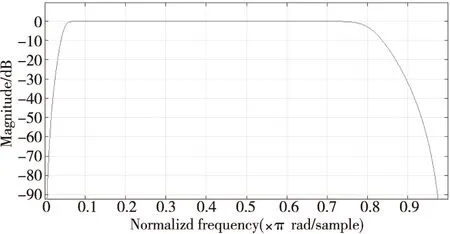
Figure 1 Frequency response diagram图1 频率响应图

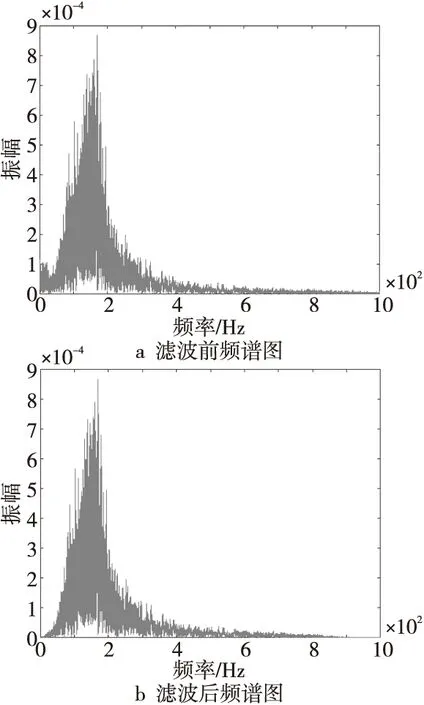
Figure 2 Spectrum comparison图2 频谱对比图

小波阈值去噪选取Db8小波基，并采用软阈值函数法对噪声小波系数进行过滤。软阈值函数计算见式(1)，其中,w是小波系数;λ是阈值;wλ是施加阈值后的小波系数。λ值利用固定阈值估计法确定,具体如式(2)所示，其中,σ是噪声标准差;Lsignal是信号长度。本文通过信噪比计算验证小波阈值的有效性。信噪比RSN如式(3)所示:

(1)

(2)

(3)

其中,S′为滤波后的信号;S为滤波前的信号。

2.4 心音特征图

MFCC特征目前被广泛应用到心音处理，它首先把心音信号转化为短时平稳数据，再向人耳听觉机理方面转化从而提取心音特征。文献[12,13]表示在卷积神经网络应用中，梅尔频率谱系数MFSC(Mel-Frequency Spectrum Coefficients)相对MFCC减少了离散余弦变换，使得特征表达更加丰富。心音信号是一维数据，为符合卷积神经网络深度学习数据格式，本文把心音信号的MFSC特征图及其一阶差分(Δ)和二阶差分(Δ-Δ)合并成3通道二维数据格式,如图3所示。

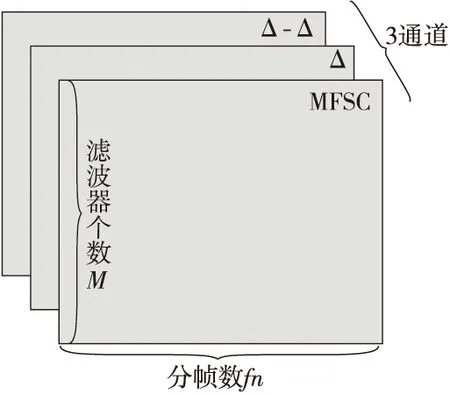
Figure 3 Heart sound feature map图3 心音特征图

2.4.1 计算MFSC

本文提取MFSC特征的步骤如下所示：

(1)预加重。将心音信号进行高通滤波，提升高频频带使心音频谱变得平坦，且突出高频共振峰。

(2)分帧和加窗。利用汉宁窗函数对信号进行加窗和分帧处理，使得心音信号变得短时平稳，方便后期研究。使用汉宁窗函数减少了2帧之间变化引起的能量泄露，同时削弱了后期傅里叶变换引起的栅栏效应。分帧窗口长度为1 024，帧移为512，2帧之间50%的重叠保证了参数过渡自然。分帧数fn计算如式(4)所示:

fn=(N-Noverlap)/Ninc

(4)

其中，N为帧长;Noverlap为2帧重叠部分;Ninc为帧移。

(3)计算谱线能量。相较于在时域视角下表征，心音信号在频域视角通过能量分布进行表征更为直观，便于观察，故对分帧和加窗后的各帧信号进行快速傅里叶变换，得到各帧的频谱X(i,k)，并对其取模平方得到语音信号的谱线能量E(i,k)，其计算如式(5)所示：

E(i,k)=|X(i,k)|2

(5)

其中,i为心音的帧数;k为谱线的频率序号。

(4)计算Mel滤波能量。通过Mel滤波器计算每帧谱线的滤波能量。把每帧的谱线能量乘以Mel滤波器的频域响应并相加。Mel滤波能量的计算如式(6)所示：

(6)

其中,S(i,m)为心音第i帧对应的第m个Mel滤波器的能量;Hm为第m个Mel滤波器频率响应;n为心音第i帧n条谱线。

(5)Mel能量取对数得到MFSC。人耳感知是非线性的，通过对每帧Mel能量取对数来模拟非线性关系，描述人耳对心音判断的感知特性。

2.4.2 构建心音特征图

心音信号是连续的时序数据，分帧提取的特征信息具有时序局部性，为了保留心音时序特征增加了前后帧信息，采用一阶差分(Δ)和二阶差分(Δ-Δ)实现。心音数据集每个心音长度不一致，导致MFSC特征长度不一，为了对齐特征，将梅尔滤波器个数设为200，截取心音信号前200帧，去掉总帧数不够的心音数据，最终得到大小为200×200的二维心音MFSC特征。对齐的MFSC特征取一阶和二阶差分，保留了心音信号时域连续性特征。将MFSC特征图和一阶、二阶差分特征图组织成3通道的三维数据格式，其大小为200×200×3。

3 CBAM注意力机制

对于输入特征图F大小为HⅹWⅹC(H为高度，W为宽度，C为通道数),CBAM依次推导出通道注意力图Mc∈R1×1×C和空间注意力图Ms∈RH×W×1,整体的注意力图计算过程如式(7)和式(8)所示：

F′=Mc(F)⊗F

(7)

F″=Ms(F)⊗F′

(8)

其中，⊗为逐元素相乘，F′为F施加通道注意力掩码后的输出，F″为F先后施加通道注意力和空间注意力掩码后的输出。

CBAM可以无缝集成到任何CNN架构，强调或抑制输入特征图，并细化其局部特征，在保持较小开销的前提下提升基线网络性能。Woo等[14]通过消融实验证明了对输入特征图先施加通道注意力后施加空间注意力运算，能够更好地提取目标特征,且空间注意力卷积核大小为7×7时，效果更好。

3.1 通道注意力

Mc(F)=σ(MLP(AvgPool(F))+

MLP(MaxPool(F)))=

(9)

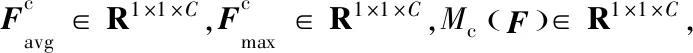
3.2 空间注意力

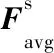
Ms(F)=σ(f7×7([AvgPool(F);MaxPool(F)]))=

(10)

4 Focal Loss损失函数

衡量2个分布的差异，经常使用交叉熵CE(Cross Entropy) 损失函数，针对二分类问题CE损失函数计算如式(11)所示。其中，p表示预测样本属于1的概率;y表示真实标签。为了表示简便，用pt表示样本属于真实类别的概率，其表达如式(12)所示。由式(11)和式(12)，可知CE函数表达如式(13)所示。在式(13)基础上得到Focal Loss损失函数表达如式(14)和式(15)所示。其中，参数α解决了正负样本之间的平衡问题，通过α值，调节标签为1的样本对损失的贡献度；通过调节参数γ，使得样本越易分类(pt值越大)，损失贡献越小，难例则相反。

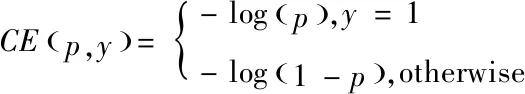
(11)

(12)

CE(p,y)=CE(pt)=-log (pt)

(13)

(14)

FL(pt)=-αt(1-pt)γlog(pt)

(15)

5 实验

5.1 数据准备

本文分别选取数据集中正常心音和异常心音的10%作为测试集(Test)。在剩下的90%数据中，分别选取正常心音和异常心音数据的80%作为训练集(Train)，20%作为验证集(Validation)。数据划分具体见表1。

Table 1 Data partitioning表1 数据划分

5.2 实验环境

本文采用TensorFlow深度学习框架。训练服务器参数为：CPU(3.2 GHz)、GPU(TITAN RTX 24 GB)、RAM(13 GB)。

5.3 网络模型及实验设计

5.3.1网络模型

ResNet152[15]以跨层连接瓶颈结构进行组合，解决了深层网络梯度消失的问题。CBAM注意力机制通过改进瓶颈结构中残差支路输出，实现残差特征图细化，使得部分特征得到强调或抑制。瓶颈结构改进模型如图4所示。当输入X与输出F″大小相同和不同时，瓶颈结构改进算法分别如式(16)和式(17)所示，为了简便公式，忽略了偏差参数。

y=CBAM(F(X,{Wi}))+X

(16)

y=CBAM(F(X,{Wi}))+WsX

(17)

其中，CBAM(·)表示通道注意力和空间注意力机制运算;F(X,{Wi})表示瓶颈结构中的3个卷积操作，卷积核分别为1×1,3×3和1×1;Wi为需要训练获得的权重矩阵;Ws为需要训练获得的使输入X和输出F″大小相同的卷积操作矩阵。

Figure 4 Improved bottleneck图4 改进的瓶颈结构

浅层卷积操作可以获取更多心音细节特征，深层卷积操作可以获取更多心音包络宏观特征，多尺度特征可以更好地表征心音信号。多组不同通道数瓶颈结构组成4个网络层，分别包含的瓶颈结构数为3,8,36和3，每层瓶颈结构卷积核1×1,3×3和1×1对应的通道数分别为(64,64,256),(128,128,512),(256,256,1 024)和(512,512,2 048)。4个网络层输出特征进行串联即为心音多尺度特征。

模型采用ReduceLROnPlateau学习率策略，每10次迭代后，如果验证集损失没有减少则初始学习率乘以系数0.8；更改ResNet152网络分类层为二分类和激活函数为Sigmoid；利用Adam优化器和Focal Loss损失函数(其中α为0.25、γ为2)进行模型编译；网络训练批次大小设置为100，迭代500次。

5.3.2 实验设计

为验证CBAM注意力机制、Focal Loss损失函数和多尺度特征可以促进ResNet152模型正确分类心音数据，共设计5组对比消融实验。通过与先前学者的心音分类效果横向对比分析，来验证改进后ResNet152模型的有效性。

5.4 实验评价指标

本文采用灵敏度Se(Sensitivity)、Sp特异度(Specificity)和准确率Acc(Accuracy)作为分类评估指标，其计算如式(18)～式(20)所示:

(18)

(19)

(20)

其中，TP表示阳性心音样本判别为阳性的心音数，FN表示阳性心音样本判别为阴性的心音数，FP表示阴性心音样本判别为阳性的心音数，TN表示阴性心音样本判别为阴性的心音数。

5.5 实验结果与分析

表2为5组对比消融实验在测试集上的测试结果，对其分析如下：

(1)实验2和实验1对比可知，CBAM注意力机制提高了基线网络ResNet152的分类准确率，但幅度不大。

(2)实验3和实验1对比可知，Focal Loss损失函数使基线网络分类灵敏度提高2.55%，但特异度和准确率提高效果不太明显。

(3)实验4和实验1对比可知，多尺度特征使得基线网络分类灵敏度和准确率分别提高了2.7%和2.64%，特异度提高效果不太明显。

(4)5个实验对比可知，CBAM注意力机制、Focal Loss损失函数和多尺度特征共同使用达到基线网络最好的分类效果，相对基线网络，灵敏度、特异度和准确率分别提高了2.85%,3.35%和3.89%。

Table 2 Experimental results表2 实验结果 %

基于CinC2016心音数据，横向对比实验5与其他学者采用深度学习方法实现的心音分类研究成果，因准确率计算公式不同，故只进行Se和Sp标准比较，结果如表3所示。

Table 3 Comparison of classification results 表3 分类结果比较 %

通过比较实验5与3种深度学习心音分类模型的分类结果，可知：

(1)相对于模式1，实验5分类结果灵敏度比较高，能够更准确判断异常心音；实验5特异度除了比文献[2]中的模式1分类结果低3%，比其他都高，因此实验5在保证高分类灵敏度的同时，能够实现对正常心音信号的正确判断。

(2)相对于模式2，实验5分类灵敏度偏低，但分类特异度相对于Potes等和韩威等的方法分别提高了13.82%和2.49%。由此可知，机器学习与深度学习模型组合、利用特征工程获取心音特征可以提高心音分类准确度；利用CBAM注意力机制、Focal Loss和多尺度特征等技巧优化深度学习模型，同样可以达到不错的心音分类效果。

(3)相对于模式3，实验5分类整体效果有些逊色。Chen等利用ECG信号准确分段心音信号，增强了心音段信号的有效性，但需要额外计算S1、S2、收缩期和舒张期确切位置；Han等引入阈值映射心音段类别到心音实例类别，增广数据集的基础上，还需额外训练阈值，使得网络模型变得复杂。由此可见，数据集的有效增强、增广可以更好地实现心音信号分类，但实验5满足了特征获取简易、网络模式简单、分类准确率较高的需求。

6 结束语

以心音特征获取简易、深度学习网络模型简单为依据，本文改进了ResNet152残差网络对CinC2016心音数据进行深度学习，利用CBAM注意力机制改进残差网络中的瓶颈结构，使用Focal Loss损失函数获取心音多尺度特征。通过5组消融实验证实了CBAM注意力机制增强了提取特征的有效性；Focal Loss损失函数减弱了心音数据不均衡带来的影响，同时促进了心音难例分析；多尺度特征提高了心音分类的准确度。与先前学者心音分类研究成果相比，本文设计的心音分类网络具有较好的灵敏度和特异度，且具有特征获取简易、网络模型简单等特点。