基于Stewart平台的空间挠性体振动复合控制

喇启云，周徐斌，吕 旺，周春华

（1.上海卫星工程研究所，上海201109； 2.上海航天技术研究院，上海 201109）

日趋增加的航天任务难度伴随着航天器及其附件朝着大型化、低刚度、弱阻尼和模态密集的方向发展。航天器在工作过程中，大型空间挠性体会受到工作环境（热辐射、空间碎片、温度冲击、太阳风等）和内部扰动作用（姿态调整、轨道变化、载荷活动等）的影响[1－2]。这些因素对空间挠性体带来的影响无法避免，非常容易激起挠性体的振动。挠性振动具有时间长、频率低、幅度大等特性，它消耗航天器能量，并对航天器的安全带来巨大隐患。当航天器主体运动与挠性振动耦合时，会对航天器的指向精度和姿态稳定产生极大的影响。因此抑制空间大挠性体的振动尤为重要。

针对航天器挠性体的振动抑制问题，主要有两种振动控制方法：被动振动控制和主动振动控制。被动振动控制主要是利用阻尼材料或者在挠性体上安装阻尼器[3]来改变系统特性，其对于高频振动抑制效果较好，但应对环境变化的能力差。近年来，以分力合成、输入成型和智能材料振动控制为代表的主动振动控制方法的研究取得了重要进展。陕晋军等[4]将分力合成方法与闭环控制相结合，应用气浮模拟器，基于三自由度挠性系统进行实验，验证了该方法的可行性，证明其能够提高航天器的姿态控制精度。以压电元件为主的智能材料振动控制方法是将控制作用直接施加于挠性体进行振动控制。陈春强等[5]将悬臂板设计成电流变夹层结构，利用变刚度控制降低悬臂板的振动水平。孙杰等[6]将压电纤维复合材料分布式布置在挠性体表面，采用线性二次型最优控制算法进行主动控制，可以实现对航天器挠性振动的快速抑制。

但是，以压电元件为主的智能材料控制挠性振动的方法对于振幅大、基频小的挠性振动存在驱动力不足的问题。此外，在空间大型挠性体上布置压电驱动器会影响挠性体的收拢和展开过程，增加系统的附加质量，降低系统的可靠性。由于六自由度Stewart 平台具有刚度质量比大，承载能力高、稳定性好、抗干扰能力强等特性[7]，并且可以直接通过串联安装在航天器本体和挠性体之间，避免对挠性体的展开和收拢产生影响。因此本文采用在大型挠性体根部安装Stewart平台的方法控制挠性振动。

Wang 等[8]将积分力传感器与基于FxLMS 的自适应反馈结合，用于压电型Stewart 平台的振动抑制。Ko 等[9]提出了基于迭代学习控制的Stewart 平台振动控制方法。Beijen等[10]仅考虑了Stewart平台自身建模参数的不确定性，忽略载荷挠性模态，设计前馈控制器，降低了建模不确定性对振动控制性能的影响。上述研究未充分考虑建模不确定性对振动控制性能的影响，本文考虑了挠性体动力学模型和Stewart 平台动力学模型的不确定性，建立了以Stewart 平台跟踪误差和挠性体模态位移为状态量的复合动力学模型，并结合LQR设计了复合振动控制器，实现对挠性体的振动控制。

1 动力学建模

1.1 Stewart运动平台

Stewart 平台是一种精度高、刚度大的六自由度并联机构，主要由负载平台、集成作动器的支腿和基平台通过约束副连接组成。Stewart 平台的构型较多，其中具有标准立方体构型的6 支撑杆平台以其独特的动力学特性而更广受关注。立方体构型的Stewart平台具有各方向刚度和控制能力一致、机械构造简单、运动学和动力学原理简单、执行机构控制系统的设计方便等优点。本文选用立方体UPS（一端球铰、一端万向铰）构型的Stewart 平台进行挠性振动控制设计。

挠性振动控制平台的坐标系如图1所示。负载平台固联坐标系fp(opxpypzp)和基平台固联坐标系fb(obxbybzb)分别固联在负载平台和基平台的质心，fe(oexeyeze)为惯性坐标系。定义负载平台质心的位姿 向 量 为X=[x,y,z,φ,θ,φ]T，其中[x,y,z]T和[φ,θ,φ]T分别是负载平台质心的位置坐标和采用卡尔丹角表示的姿态角。

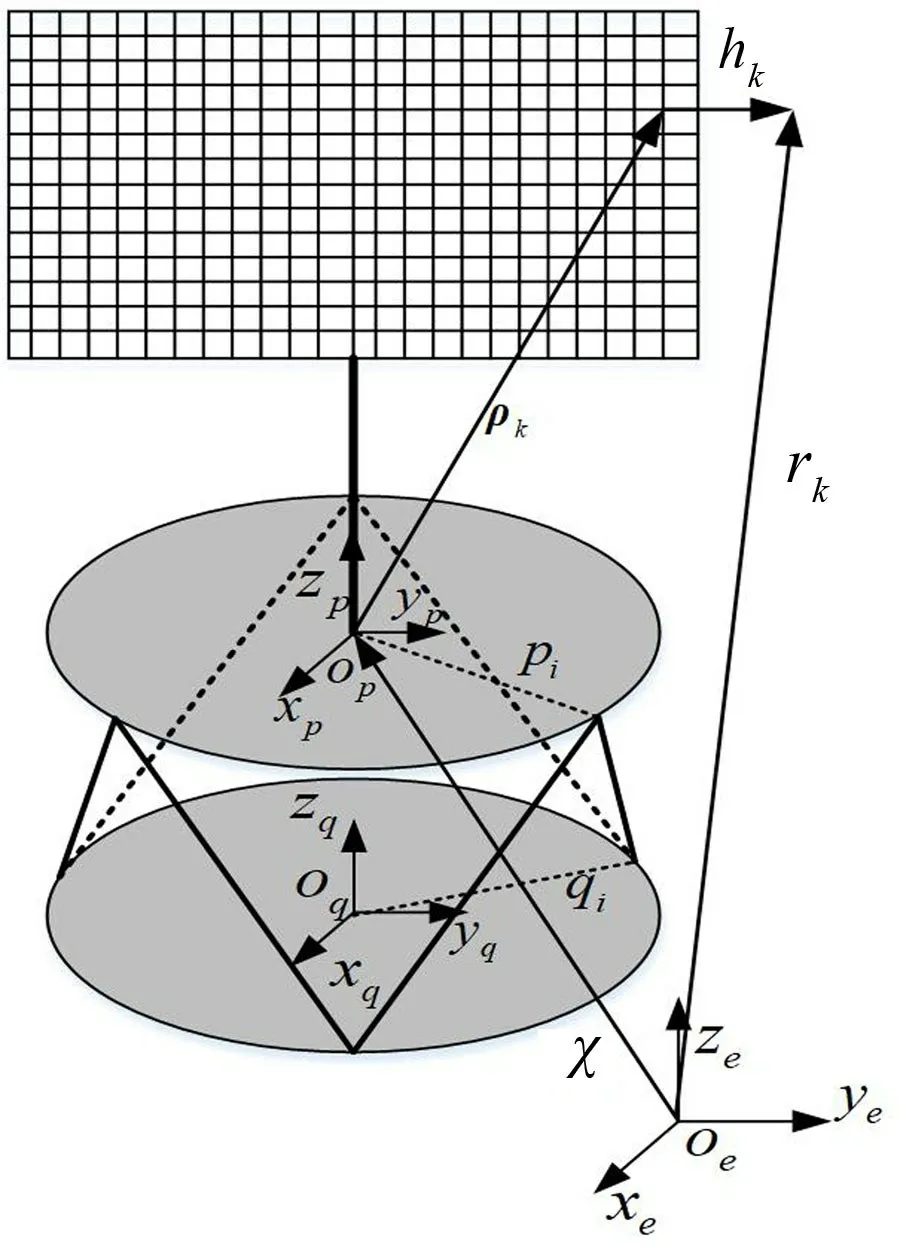
图1 坐标系统图

支腿向量的表达式：

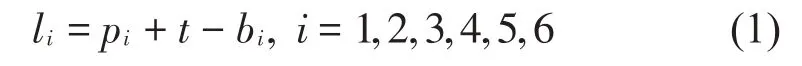
式中：li为第i根支腿的位置向量，pi和bi分别是惯性坐标系中第i根支腿与负载平台和基平台铰接点的位置向量。t为负载平台质心在惯性坐标系中的位置向量。

支腿的长度为：

支腿的方向向量为：

支腿与上平台的关系为：

式中：J为雅可比矩阵，它将上平台和支腿联系在一起。雅可比矩阵J的详细定义为：

式中：p×i(i=1,2,3,4,5,6)为向量的pi的叉乘矩阵。

由牛顿欧拉法得到Stewart平台的动力学模型：

式中：M为惯性矩阵；C为阻尼矩阵；K为刚度矩阵；Δ为负载平台动力学模型的不确定性；τ为支腿的广义驱动力向量；Br为Stewart负载平台与挠性体的转动耦合系数；Bt为Stewart负载平台与挠性体的平动耦合系数。

1.2 空间挠性体

通过有限元法求得挠性体上第k个节点的振型为：

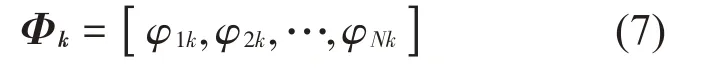
式中：k=1,2,…,n，n为采用有限元法获得的节点总数，N为振型截断数。

若模态坐标向量η表示为：

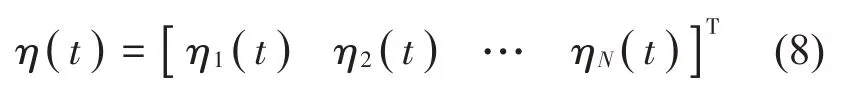
则第k个节点线位移hk表示为：

使用第二类拉格朗日方程推导挠性体的运动方程。挠性体的动能为：

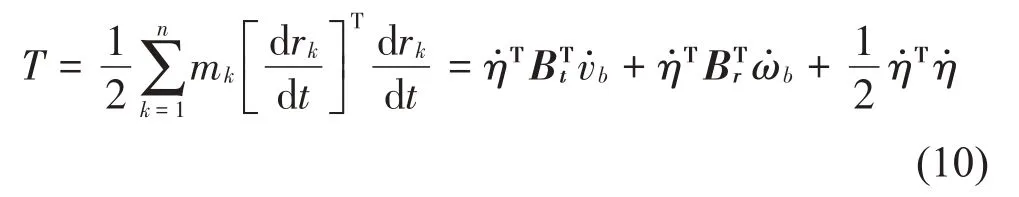
式中：rk=χ+ρk+hk，ρk为挠性体第k个节点在P系中的位置矢量。ωb和vb分别是相对惯性系的角速度和线速度。

挠性体的应变势能为：

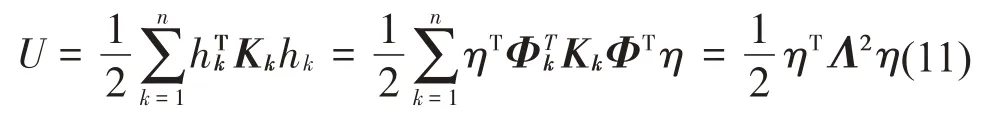
式中：Kk表示第k个节点的刚度矩阵，根据振型Φk的正交性质，有diag(ω21ω22…ω2N)表示用有限元法求得的挠性体的各阶模态频率。

挠性体的拉格朗日函数为：

挠性体的拉格朗日动力学方程为：

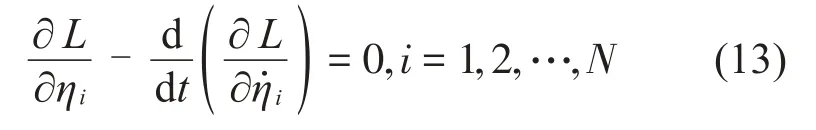
将式（10）和式（11）代入式（13）得挠性体的动力学方程：

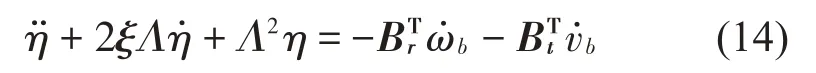
式中：ξ=diag(ξ1,ξ2,…,ξN)为挠性体阻尼矩阵。

2 考虑建模不确定性的复合振动控制器设计

由式（14）可知，Stewart 负载平台的加速度可为挠性体提供控制作用，分开设计振动控制器和Stewart 平台运动控制器。LQR 控制方法仅适用于挠性体动力学表达式（14）的控制律，得到期望的Stewart平台位姿Xdc后设计Stewart 平台运动控制器，以跟踪期望位姿Xdc。

挠性体第k个节点在fe(oexeyeze)系中的位置矢量为：

当Stewart 负载平台的跟踪误差exd=Xd-X和挠性体的振动为0 时，挠性体和Stewart 负载平台的运动等效为刚体运动，其中Xd为负载平台的位姿指令。为了抑制挠性体的振动，得到期望的负载平台位姿Xdc，相应的跟踪误差为ex=Xdc-X。当ex和exd为0 时，由两个跟踪误差相减可得exm=exd-ex=Xd-Xdc为0，因此可以Xdc跟踪Xd。误差exm的相应动力学方程可以写为：

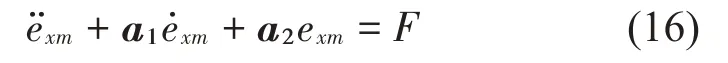
式中：a1和a2是常系数矩阵，F是虚拟控制力，可控制exm趋于0。

误差ex的动力学方程可写为：

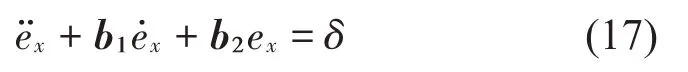
式中：b1和b2是常系数矩阵，由Stewart 平台的控制律确定，δ为Stewart 平台动力学模型的不确定性和挠性体动力学模型的不确定性之和。

将式（17）代入式（16），可得误差exd的动力学方程：

再将式（18）代入式（14），得复合动力学方程为：

式中：B=[BTt BTr]

将式（19）进一步写为：

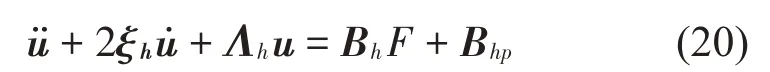
式中：ξh和Λh分别为阻尼矩阵和刚度矩阵，Bh为控制增益矩阵。

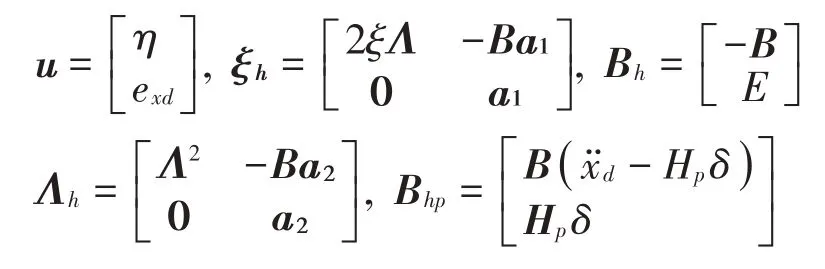
由式（20）得状态空间方程：

式中：

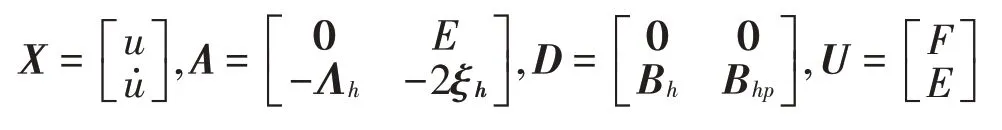
利用LQR 控制方法设计振动控制器得到虚拟控制力F。定义系统的二次型性能泛函为：

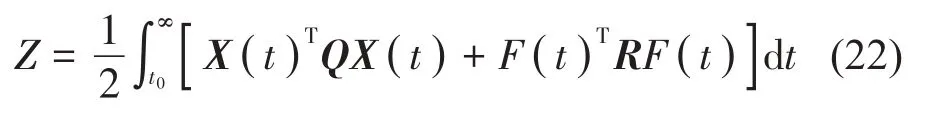
式中：Q为半正定矩阵，R为正定矩阵。为了确保Z取到极小值，需要在从t0开始到无限时刻结束的区间内，寻找并计算得到最优控制量F，系统从初始状态X0向稳态方向发展。

系统Riccati方程为：

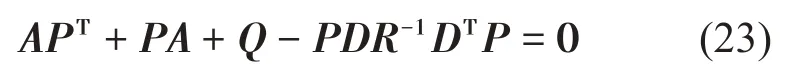
最优控制量：

式中：P由系统Riccati方程求得，F可由U获得。

3 挠性太阳阵振动控制仿真分析

用于挠性体振动控制的闭环系统原理框图见图2。由状态空间方程式（21）以及LQR控制方法得到虚拟控制力F，将F代入误差exm的动力学方程（16）中得到期望的负载平台位姿Xdc，由于滑模控制方法抗干扰鲁棒性好，适应于变体控制系统，因此本文选用滑模控制设计Stewart平台的控制器，跟踪负载平台期望位姿Xdc。

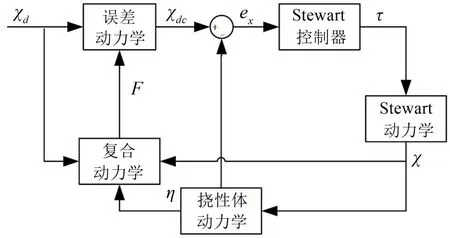
图2 闭环控制系统图

选择大型挠性太阳阵作为仿真对象，太阳阵的质量特性参数和挠性参数以及立方体UPS 构型的Stewart平台的基本参数如表1所示。

表1 太阳阵和Stewart平台的基本参数

太阳阵尺寸/m太阳阵质心（fp坐标系）/m太阳阵转动惯量/（kg·m2）太阳阵前3阶频率/Hz太阳阵前3阶阻尼比ξ平动耦合系数Bt 3×1.5×0.015[0.007 0 1.9]T diag[69.23,2.69,68.61]0.705,1.293,1.783 0.01,0.01,0.01■ ■■■2.80 0 0 0 0 0 0 2.83 0■ ■■■转动耦合系数Br负载平台半径/m基础平台半径/m平台高度/m负载平台转动惯量/（kg·m2）作动器阻尼矩阵/N·s·m-1作动器刚度矩阵/N·m-1 0 7.64 0 0 0 -1.44-7.61 0 0 0.256 0.256 0.1732 diag[0.154,0.308,0.154]diag[20,20,20,20,20,20]diag[1,1,1,1,1,1]×105■ ■■■■ ■■■

复合动力学方程中常系数矩阵a1、a2、b1、b2取值分别为：

a1=diag(20…20)18×18

a2=diag(30…30)18×18

b1=b2=diag(10…10)18×18

最优控制器的控制参数Q和R分别为：

Q=diag(500…500)18×18

R=diag(0.5…0.5)18×18

选取惯性坐标系fe与初始负载平台固连坐标系fp重合，Stewart 负载平台的初始位姿X0=[0,0,0,0,0,1]T。前10 s 关闭Stewart 平台控制器，Stewart负载平台开始以平衡位姿[0,0,0,0,0,0]T为中心进行回复运动，周期为1.42 s，在Stewart负载平台回复运动的激励下，太阳阵产生衰减振动，两种运动相互耦合。第10 s开启Stewart平台的控制器，抑制太阳阵的振动。太阳阵的模态响应曲线如图3所示。激励主要引起太阳阵1 阶弯曲振动，第10 s后1阶振动得到迅速抑制。

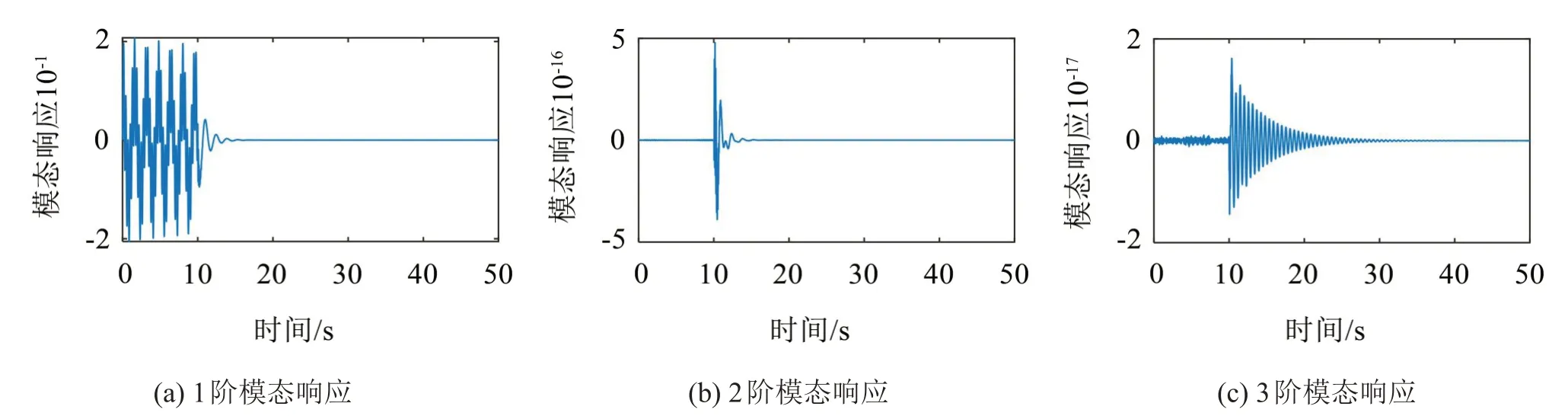
图3 太阳阵模态响应曲线

图4是Stewart平台6条支腿作动器的广义驱动力曲线，支腿作动器1、2和6主要为抑制太阳阵1阶弯曲振动提供驱动力。图5是由复合控制器获得的Stewart 平台的期望位姿Xdc和实际位姿X，从第10 s开始，实际位姿X跟随期望位姿Xdc变化使太阳阵的挠性振动迅速衰减，且Stewart 平台的位姿趋于稳定。

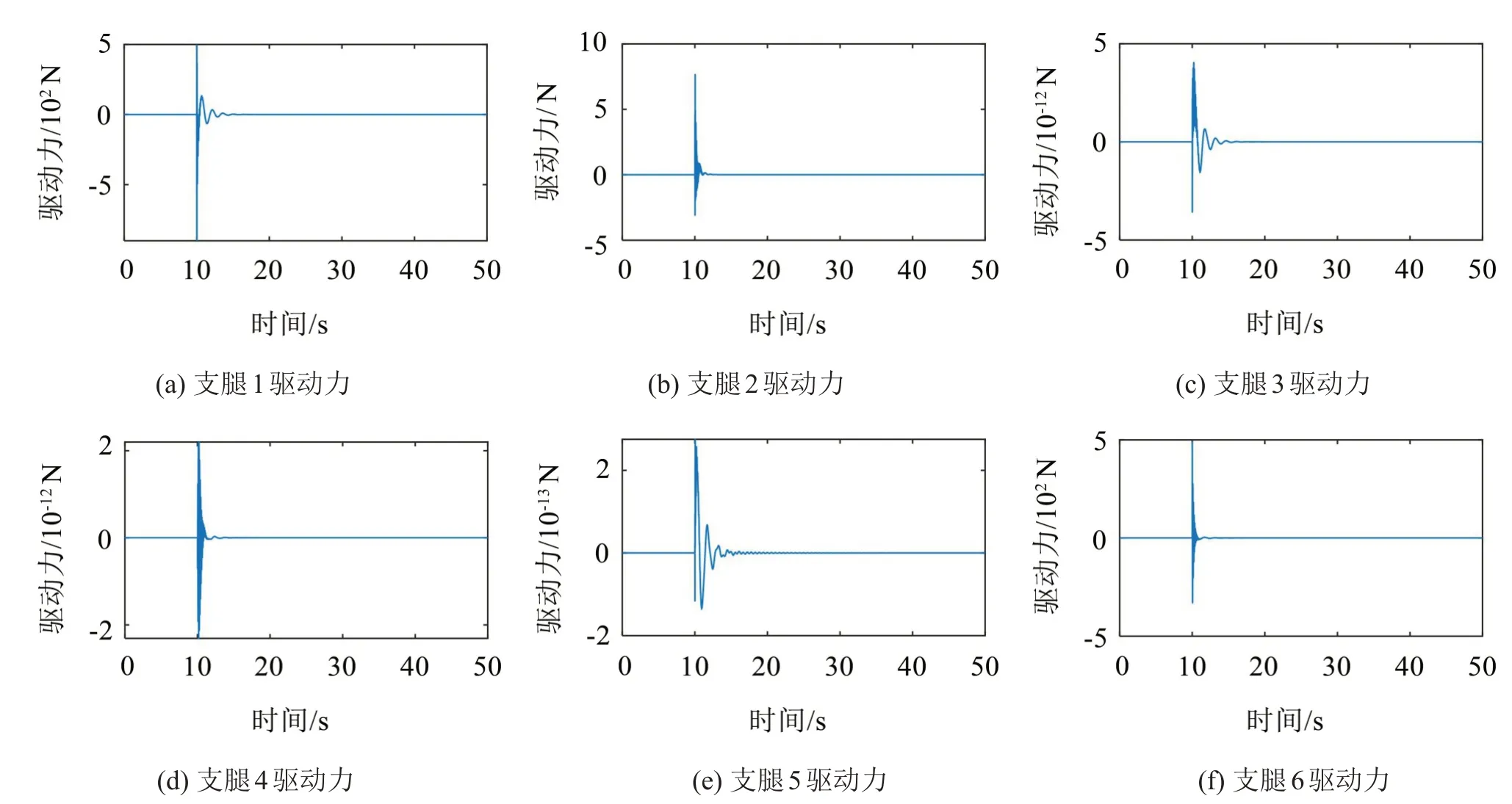
图4 6条支腿广义驱动力曲线

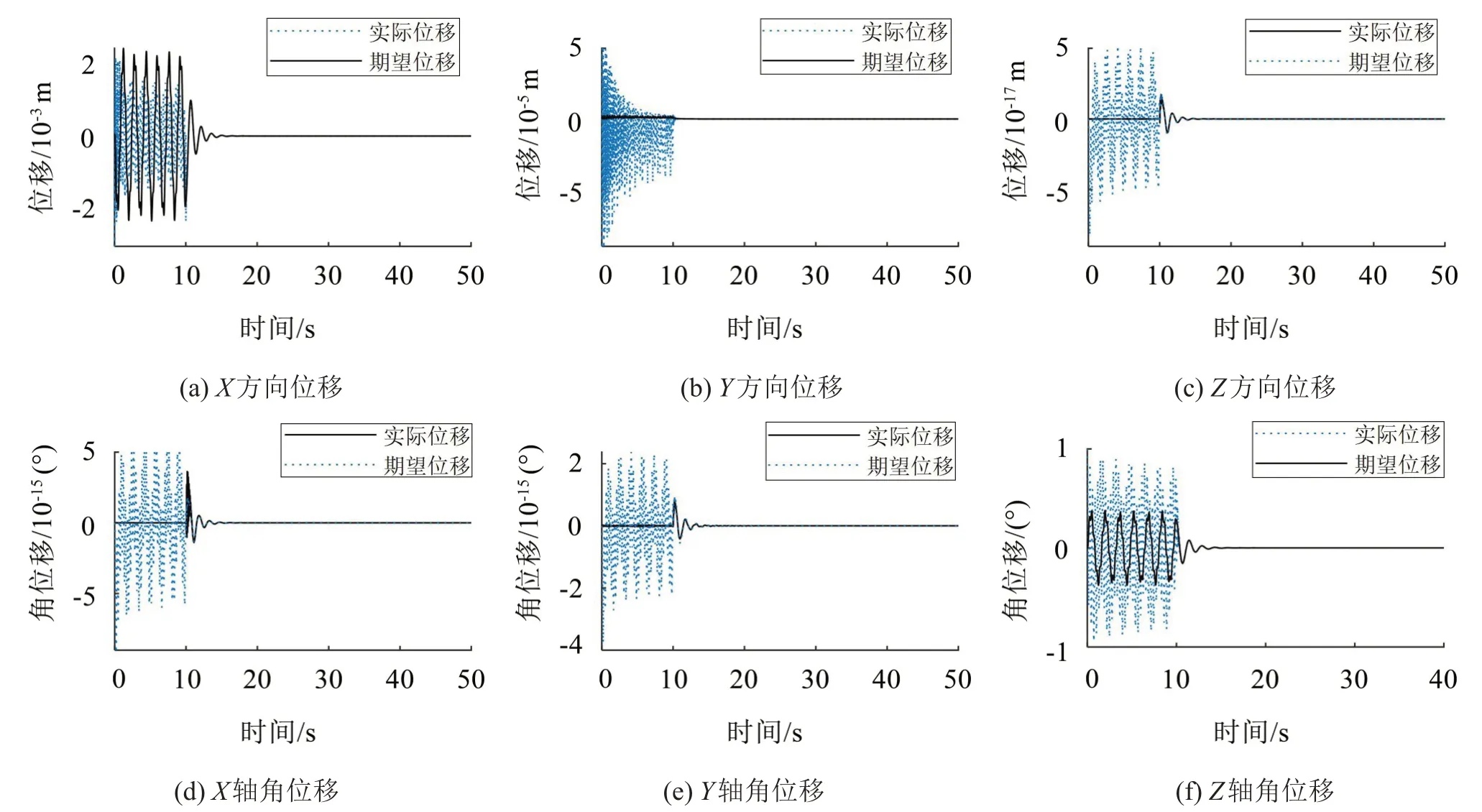
图5 Stewart平台位姿曲线

4 结语

本文针对空间大型挠性体的振动控制问题，采用在挠性体根部安装Stewart 平台的方法来控制挠性振动，并提出一种复合振动控制器的设计方法。主要结论如下：

（1）为了便于执行机构控制系统的设计，更加快速准确跟踪控制指令，选用立方体UPS 构型的Stewart平台，采用牛顿欧拉法建立Stewart平台动力学模型。挠采用有限元法结合拉格朗日函数建立空间挠性体的振动方程。

（2）针对Stewart平台动力学和空间挠性体动力学建模不确定性，设计了复合振动控制器，利用LQR控制方法设计跟踪误差和模态位移的复合动力学的控制律，得到Stewart 上平台的期望位姿χdc，然后设计Stewart 平台运动滑模控制器，以跟踪期望位姿χdc，实现对挠性体的振动抑制。

（3）仿真结果表明，所采用的基于Stewart 平台的空间挠性体振动复合控制方法能够有效抑制挠性振动，同时该方法可应用于空间大型挠性体的精确定位和振动抑制。但本文尚未考虑低频模态密集情况下的控制问题，尚未进行姿态机动过程中挠性体振动控制效果的研究，这些需在后续研究中进一步考虑。