搭载分数槽永磁电机的电驱动总成振动控制
2022-08-19葛帅帅
郭 栋,任 杰,葛帅帅,张 韬,周 仪
(重庆理工大学 车辆工程学院,重庆 400054)
分数槽永磁同步电机绕组利用率高,可以有效削弱磁极非正弦分布导致的高次谐波,减小齿谐波电势,在电动车领域得到广泛引用[1-3]。随着电驱动总成向轻量化、高功率密度化发展,越来越多的企业将电机转轴与减速器传动系统通过花键连接起来,形成电机-减速器耦合的电驱动总成系统。相较于早期方案,集成化的电驱动总成结构紧凑,功率密度高且带来较高的扭矩容量,但电磁激励与齿轮激励的共同作用使得电驱动总成系统具有更加复杂的振动特性。
目前,对电驱动总成进行研究时常将电机与减速器作为单独的个体处理。其中由于分数槽电机含有丰富的磁场谐波分量,致使电机产生低阶电磁力,振动幅值与电磁力的力波次数成反比,导致电驱动总成产生较大的振动[4-5]。除此之外,由于电机与减速器刚性连接,电机侧的振动可能引发整个电驱动总成性能下降,甚至损坏某些部件,形成安全隐患[6]。针对分数槽电机谐波磁动势导致的振动问题,有些学者[7-10]将提取出的径向电磁力离散成点,加载到定子齿面,搭建磁固耦合模型,分析磁场作用下定子系统的振动特性,该方法可精准反映电机振动的频谱特性;有些学者[11-12]则引入单元电机的概念,探究不同的极槽配合对径向电磁力波阶数的影响;也有学者[13]从变频器角度出发,构建二维场路耦合模型,计算不同力波作用下的结构响应,结果表明供电产生的谐波会恶化振动性能;同时主动注入谐波电流、改变绕组接法等方式可以减小磁场谐波,在提高电机效率的同时也削弱了径向电磁力波[14-15],但这无疑会增加电机的控制难度。在减速器侧,有些学者[16-17]将传动系统作为主要研究对象,考虑了齿轮系统的啮合冲击,建立传动系统振动分析模型,对轴承动载荷下减速器箱体的振动响应进行预测,指出减小齿形误差对抑制振动有重要意义。有些学者[18]运用PloyMAX法识别减速器的各阶模态,并在此基础上考虑齿轮啮合激励,发现了易引起共振的工况,但并未给出优化方案。综合来看,以上研究都仅仅涉及电机或者减速器,没有考虑二者刚性连接后对模态的影响,无法准确反映电驱动总成在实际工作环境下的振动特性。
针对以上问题,本文以某电动车电驱动总成为研究对象,首先对电驱动总成进行整车试验,获得其声振信号,随后从气隙磁场入手,采用磁势乘磁导法计算10极12槽电机电磁力波的频率及空间模数,结合电机电磁模型,提取出引起振动的低阶电磁力波。建立减速器刚柔耦合模型,计算出不同位置的轴承动态力,并利用模态敲击试验验证电驱动总成壳体振动响应模型。在电磁激励以及轴承动态力的共同作用下,电驱动总成在最高转速运行工况下振动响应剧烈且存在共振现象,针对振动的主要贡献侧-分数槽永磁电机,考虑工艺及成本,从辅助槽、转子分段斜极两个方面进行电磁优化。该研究可为电驱动总成的设计与优化提供理论指导。
1 电驱动总成整车NVH测试分析
试验对象为某国产电驱动总成,搭载分数槽永磁电机,其参数如表1所示。为总结电驱动总成振动特性,试验时分别在电机壳体、减速器壳体布置了声压传感器和三向振动传感器,采集了整车状态下电驱动总成的声振信号。试验工况包括:

表1 分数槽永磁电机参数
(1)加速工况,电动车电机轴转速以最大加速度从0加速到最高转速5 300 r/min;
(2)稳态工况,分别记录电动车在1 325 r/min、2 650 r/min、3 975 r/min以及5 300 r/min工况下的声振信号。
图1为电机侧麦克风噪声,测试数据表明噪声具有明显的阶次特征,对应的振动响应频率为电流频率的偶数倍频,且在890 Hz 与1 176 Hz 处存在明显的共振带。
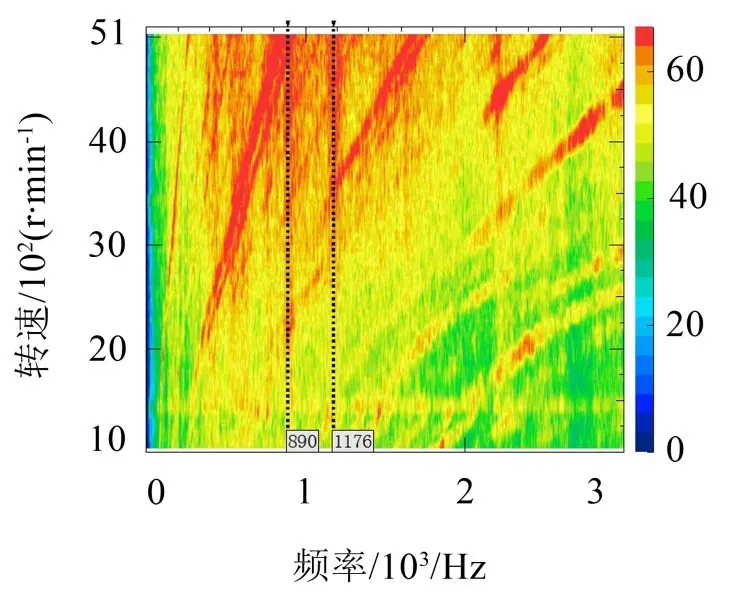
图1 电机壳体噪声Colormap图
图2为不同转速下壳体的径向振动加速度,电动车以最高车速运行时,电机壳体振动加速度远高于其余转速工况,幅值达到了2倍以上,且振动频带较宽。
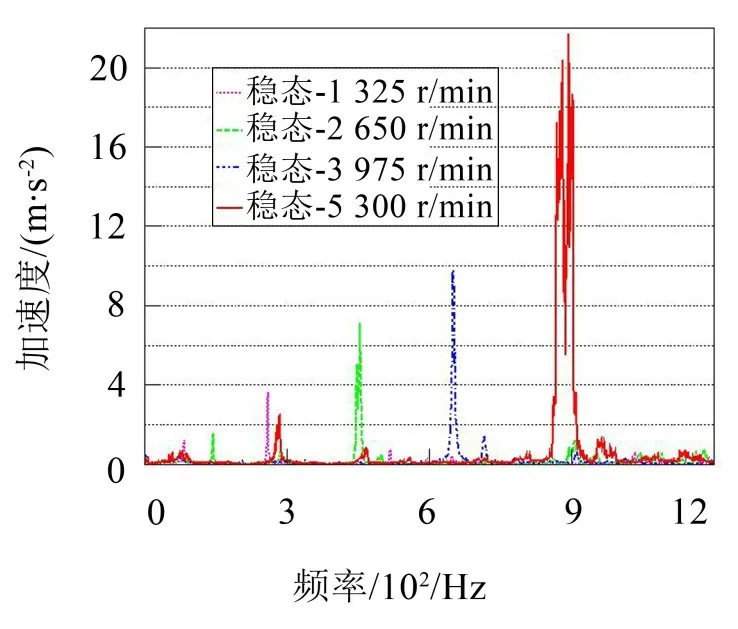
图2 电机壳体径向振动加速度频谱图
2 电驱动总成激励分析
为了准确预测总成壳体振动响应,对电驱动总成的激励源进行梳理。在电机侧,定子铁芯上的电磁激励可分为切向电磁力和径向电磁力,切向电磁力主要引起电机转矩脉动,对定子系统振动的影响较小,故主要考虑径向电磁力;在减速器侧,壳体振动主要由齿轮激励引起。因此,为分析电驱动总成振动响应阶次特性的试验现象,对电机侧的径向电磁力波以及减速器齿轮激励进行分析。
2.1 气隙磁场
忽略铁心磁饱及磁阻,气隙磁场可由定转子磁势之和与气隙磁导相乘得到:
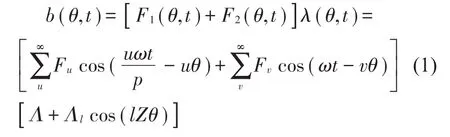
式中:F1(θ,t)为永磁体恒定磁势在气隙处引起的转子谐波磁势,F2(θ,t)为实现三相电流平衡后的定子绕组合成磁动势,ω为定子电流角频率,Λ为气隙磁导不变的部分,Λl为气隙磁导变化的部分;对于本文所关注的分数槽电机,其每极每相槽数为:
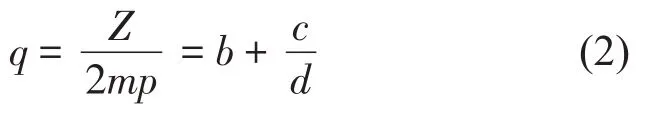
b为整数,m为电机相数,c d为最简分数,对于本文所研究的10极12槽电机,d为基数,其定、转子谐波极对数可表示为:
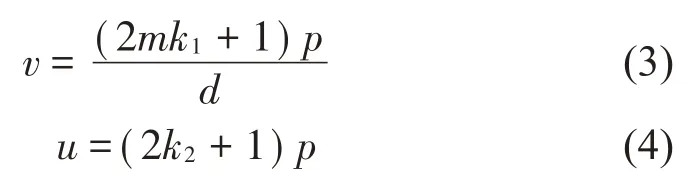
代入定、转子磁场谐波极对数,对分数槽永磁电机径向电磁力波进行解析。
由表2可知,径向力波最小阶次为2,这是由于10 极12 槽永磁电机,在每极下的槽数为1.2,每5 极才能形成完成的磁路,因此整个电机只存在两条完整磁路,导致其产生了阶次比极数更低的电磁力波,相较于高阶电磁力,其对振动幅值的贡献更大,从而导致分数槽电机振动较大。
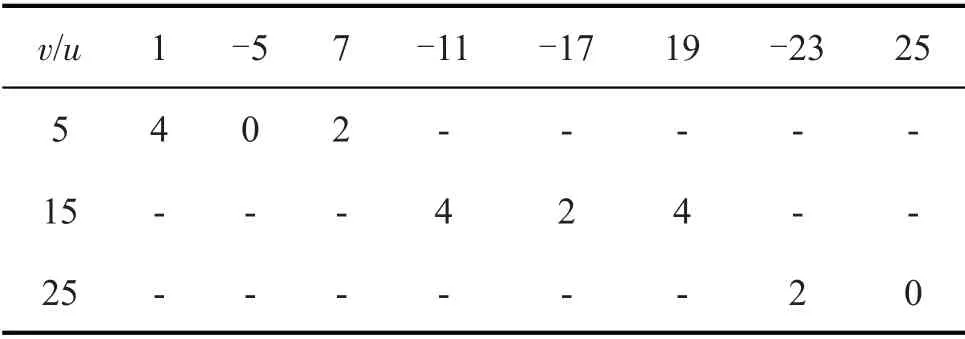
表2 分数槽永磁电机径向力波分析
通过5 300 r/min下气隙磁场中的径向力密度对电驱动总成振动峰值进行分析。通过傅里叶变换得到径向电磁力密度频谱图,如图3所示,由于0 Hz直流分量对振动噪声没有贡献,一般不予考虑;除0 Hz电磁力密度外,偶数倍及其整数倍电源频率的径向电磁力密度幅值较高,其中在883.4 Hz处最为突出。
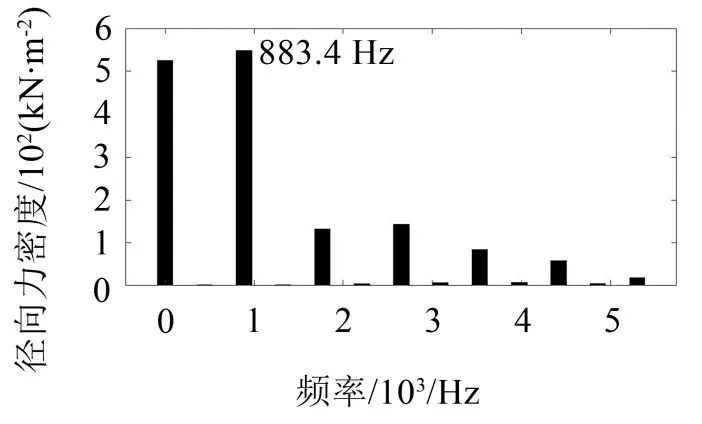
图3 径向电磁力波频谱图
2.2 减速器轴承动态力分析
该电驱动总成搭载的二级减速器齿轮参数如表3所示。齿轮激励通过齿轮轴传递到轴承,产生轴承动态力,并作用于减速器壳体,导致壳体振动。因此本文通过建立齿轮系统动力学模型,得到减速器处于不同位置时的轴承动态力。
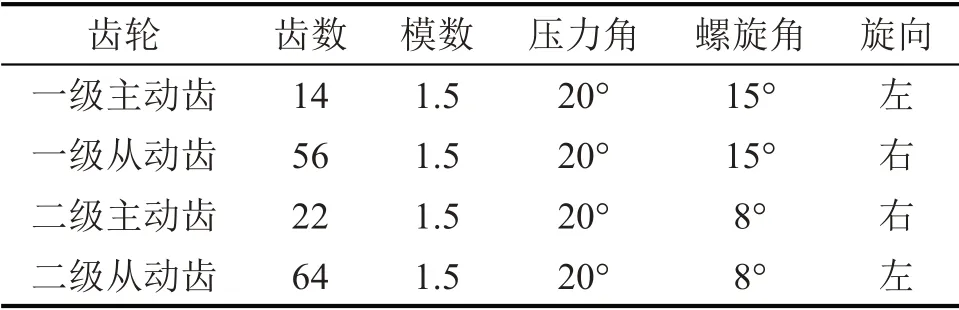
表3 齿轮副宏观参数
非旋转件通过有限元模型导入。以减速箱轴承孔坐标为参考点,调节减速器刚体模型位置,将轴承节点与刚体模型连接起来,按照整车状态进行约束。
减速器系统动力学模型如图4所示,仿真工况与试验工况一致,通过动力学计算得到减速器轴承座上6 个位置处的轴承动态力。减速器采用斜齿轮,根据左右手法则可知轴承轴向动态力指向左侧,右侧轴承处于悬置状态,轴承轴向动态力趋近于零。

图4 减速器系统动力学模型
以图5所示中间轴左侧轴承力为例,电机轴转速为5 300 r/min,一级齿轮啮合频率为1 236 Hz,二级齿轮啮合频率为485 Hz。轴承动态力主要出现在一、二级齿轮啮合频率及其倍频处。
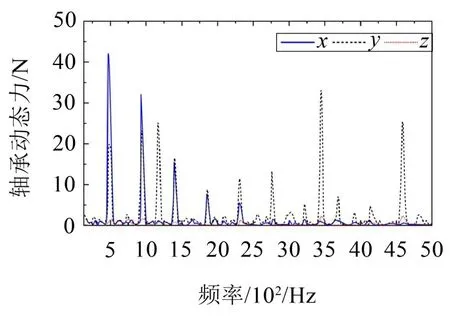
图5 中间轴左侧轴承力频谱分析
3 振动分析及控制
3.1 电驱动总成壳体有限元建模及验证
电机壳体与减速器壳体通过螺栓连接,改变了整体的刚度,对电驱动总成壳体的固有频率有一定的影响,因此为了更加准确预测电驱动总成的振动响应,有必要建立完整的结构有限元模型。定子铁芯采用硅钢片叠加而成,可有效减小涡流损耗,提高电机效率,同时也使其具有各向异性;定子绕组结构复杂,难以确保网格质量,因此为保证振动响应模型的准确性需要对电驱动总成结构进行如下合理设置:
(1)定子铁心与电机机壳进行共结点处理,模拟过盈配合;
(2)为考虑定子铁心各向异性,采用Voigt 并联模型和Reuss串联模型计算定子铁心材料参数;
(3)将绕组的质量附加到定子铁心,通过修改材料参数设置刚度;对样机进行上述的等效,得到如图6所示的电驱动总成壳体有限元模型。

图6 电驱动总成壳体有限元模型
为验证电驱动总成有限元模型的正确性,对总成壳体结构进行模态敲击试验。使用弹力绳将样机悬置,模拟与模态仿真分析一致的无约束条件。如图7所示。

图7 电驱动总成壳体模态敲击试验
沿电驱动总成壳体周向布置激励点,为减小人工敲击的误差,对同一激励点进行多次敲击,取传递误差平均值,保证结果准确性。相较于单电机,电驱动总成壳体结构更加复杂,高频模态难以激起,本文利用敲击法只得到前3阶模态。
由表4可知,通过总成壳体模态敲击试验获得的固有频率与仿真固有频率误差保持在5%以内,符合建模要求。按照总成实际工作状态固定约束,计算出约束状态前3阶固有频率。
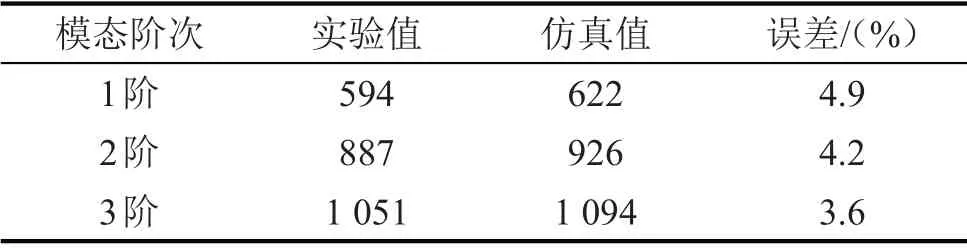
表4 试验模态与仿真模态对比/Hz
由表5可得,约束状态下总成壳体的3阶固有频率(887 Hz)与5 300 r/min转速下的电磁力波频率2f=883.4 Hz较为接近,判断出该工况下电磁力波引起结构共振是导致振动加剧的主要原因。

表5 电驱动总成壳体约束模态频率/Hz
3.2 电驱动总成振动响应分析
将电驱动总成各个位置轴承座等效成点,分别赋予X、Y、Z方向的动态力;将计算出的径向电磁力波映射到电驱动总成定子齿部。选取电机壳体与减速器壳体两个测点求取电驱动总成壳体振动响应频谱,与测试结果进行对比,如图8至图9所示。
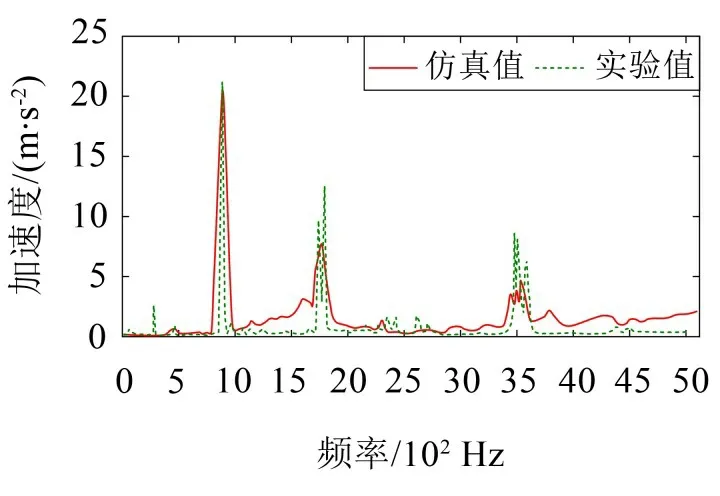
图8 电机壳体振动响应对比
由图8至图9可知:
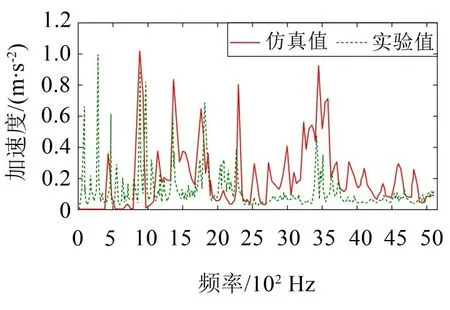
图9 减速器壳体振动响应对比
(1)电机壳体振动响应频谱在电源2 倍频及其整数倍频处出现峰值,其中2 倍电源频率与结构固有频率较为接近,导致振动加速度达到了22 m/s2;
(2)电磁激励虽未直接作用于减速器壳体,但电机壳体与减速器通过螺栓链接,使得减速器壳体同样在883.4 Hz出现振动峰值;
(3)减速器壳体的振动响应特征频率主要位于一、二级齿轮的啮合频率及其倍频处,振动峰值在2倍一级齿轮啮合频率处为0.8 m/s2。
通过上述仿真分析与实验测试可以证明径向电磁力波是引起电驱动总成振动的主要原因,齿轮啮合冲击对振动的贡献量较少,且电机壳体仿真振动响应试验结果吻合度较高,因此以降低电机壳体振动响应为目标进行优化工作。
3.3 电驱动总成振动控制
电机径向电磁力波是引起电驱动壳体振动的重要原因,目前抑制电磁振动的常用方法包括改变绕组形式、减小槽口气隙磁导变化、优化磁极形状等,其中转子开槽可以在保证电机转矩密度的情况下减小漏磁且不需要改变电机原始参数。建立转子参数化模型,为减小气隙谐波,要保证开槽位置在磁极上对称分布,对比不同槽深、槽口宽度下的气隙磁场,选取最优结果对应的方案作为本次优化方案。图10至图11为转子开槽示意图以及未开槽与开槽情况下径向气隙谐波傅里叶分解图。
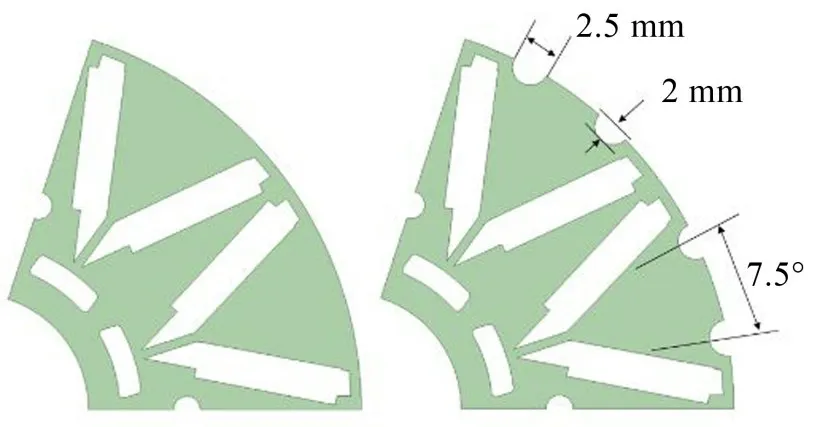
图10 转子开槽方案示意图
如图11所示,开槽后除11 次谐波稍有增大,其余各谐波分量均有所下降,特别是引起2 倍电源频率径向电磁力波的3 次谐波下降了20.5%,验证了转子开槽对气隙磁场谐波的削弱作用。
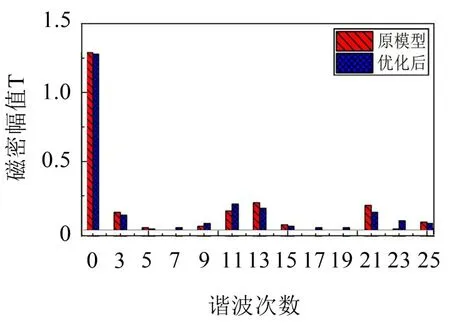
图11 转子开槽方案与原方案气隙谐波对比
永磁同步电机特有的齿槽转矩是影响电机输出性能的一个重要参数。转子分段、定子斜槽以及磁极开槽都是降低齿槽转矩和抑制转矩脉动的有效方案,相较于其他技术,转子分段斜极工艺简单,且能减小磁钢涡流损耗。在有限元模型中将转子分段,对分段数和分段角度进行参数化扫描,找出最佳优化方案。分别对原模型和优化模型进行仿真计算,得到优化前后的齿槽转矩。
如图12所示,转子分段后齿槽转矩得到大幅优化,转矩峰值由231.3 mN·m降到了142.5 mN·m,下降了38.4%。考虑到优化方案降低了气隙磁密,对优化后的平均输出转矩进行评估,仅比原方案下降0.7 N·m,对电机转矩影响不大,因此可配合转子开槽使用。
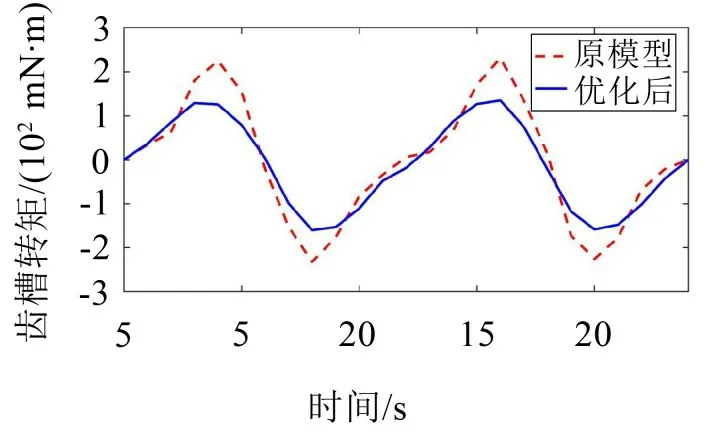
图12 转子开槽方案与原方案齿槽转矩对比
3.4 转子结构优化方案验证
优化后的电磁模型与原减速器模型耦合,搭建新的电驱动总成磁-固耦合模型,选取优化前电驱动总成壳体同一观察点,计算振动响应并进行对比。仿真结果如图13所示。
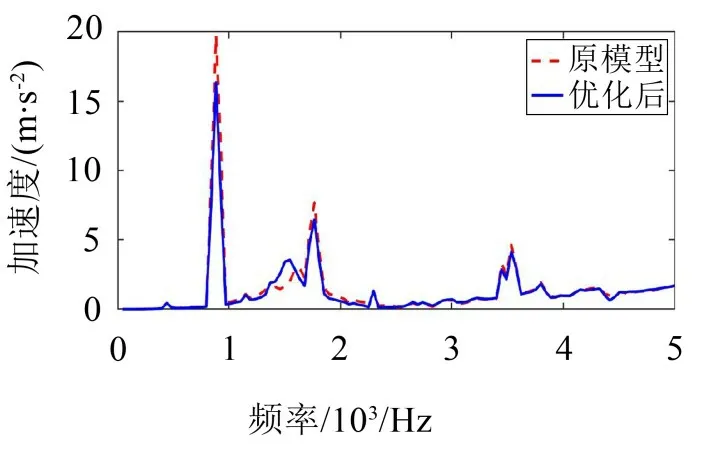
图13 优化方案与原方案振动加速度对比
优化后电驱动总成振动加速度几乎在整个频率段都有降低,峰值仍然在2倍电源频率处,但加速度幅值降低了3.6 m/s2;4倍电源频率1 766.7 Hz处振动加速度降低了1.4 m/s2,验证了优化转子结构方案抑制振动响应的有效性。
4 结语
(1)通过频谱分析,识别出电驱总成振动加剧是由于分数槽电机低阶电磁力频率接近电驱总成固有频率所导致的结构共振;
(2)由于分数槽电机完整磁路较少,因此在定、转子磁场作用下更容易产生低阶电磁力;
(3)电驱动总成结构复杂,充分考虑电机壳体定子硅钢片的各向异性以及绕组对电驱动总成刚度的影响,可建立更精准有效的结构有限元模型;
(4)转子开槽可有效抑制气隙磁场谐波,结合转子分段斜极以优化径向电磁力波、削弱齿槽转矩,可抑制电驱动总成壳体振动响应。
