基于松耦合法的π型主梁竖向涡振数值模拟

王向阳，张帅辉

（武汉理工大学 交通与物流工程学院，武汉 430063）

现代桥梁由于跨径的增大以致结构刚度不断下降，而结构的轻柔致使其对外部风环境十分敏感，目前风致桥梁振动问题已经成为大跨桥梁施工及运营阶段抗风设计必须着重考虑的控制因素[1]。桥梁涡激振动是风与结构相互作用产生的一种振动形式，是由流经桥梁上下表面的流体所产生的交替脱落旋涡引起的限幅振动现象。当旋涡脱落频率接近结构的某阶自振频率时就会发生共振，此时桥面振幅骤增严重影响行车安全以及降低结构疲劳寿命[2]。近几十年来，由于桥梁涡振现象频发，国内外学者对此展开了大量研究，从而在涡振的机理、影响因素以及抑振措施等方面取得一定的进展[3]。其主要研究方法逐渐从完全依赖传统的风洞试验过渡到数值模拟与试验相结合，这一定程度上弥补了风洞试验耗资大、周期长等不足，同时也说明数值模拟技术的可行性。国外学者Frandsen 等[4]基于有限元方法和动网格技术对大带东桥进行涡激振动的全耦合模拟，其计算结果同其他研究数据相比较为吻合；Uenal 等[5]通过对一个近尾迹流场的计算分析发现4 种基于RANS（Reynolds Average Navier-Stokes）的湍流模型中SST（Shear Stress Transport）湍流模型模拟结果最准确；Daniels 等[6]采用大涡模型对矩形柱进行强迫振动模拟，得到了比较准确的计算结果；国内学者徐枫 等[7]将Newmark-β法写入UDF（Users Defined Functions）并结合FLUENT 中的动网格技术成功观测到柱体的锁定、“拍”以及位移失谐的现象；陈文礼等[8]基于雷诺时均应力模型模拟得到了圆柱涡致振动的风速锁定区域，且与试验结果吻合较好；李永乐等[9]基于CFD（Computational Fluid Dynamics）和CSD（Computational Structural Dynamics）耦合的方法较好地模拟了方柱风致振动中的流固耦合效应。

以上研究的断面形状较为规则，且多为风洞试验的验证性研究。本文以π 形主梁断面为研究对象，基于松耦合方法通过Newmark-β数值解法结合FLUENT中的二次开发接口来获取断面的涡激振动响应，采用“刚性运动区域+动网格区域+静止网格区域”的方法分块划分网格[10]，通过网格光顺和重构改善网格运动过程中的质量问题。在验证该方法正确性的基础上，建立一座拟建斜拉桥的有限元动力模型，根据获取的动力特性参数对其进行风致涡振模拟，根据该模拟结果可初步判断该桥梁的涡振性能，同时也可为后续的风洞试验奠定一定基础。

1 松耦合方法

松耦合法在不同学科中均有广泛应用，对于气动弹性问题，王少波等[11]通过CFD+CSD结合的方式给出基于松耦合法求解该问题的一般思路。针对本文中的涡激振动问题，首先在分析结构的竖向振动时将其看作是单自由度的弹簧振子系统，然后利用FLUENT 中的二次开发功能，将求解结构竖向动力方程的Newmark-β方法以及FLUENT中特有的宏命令写入自编UDF 中与FLUENT 进行对接。开始计算时先求解每个时间步内系统的流体控制方程，并通过宏Compute_Force_And_Moment 提取结构上的升力，然后通过上述UDF中的Newmark-β数值方法求解在升力作用下结构的竖向运动方程从而得到位移、速度等物理量；再将在上一步得到的物理量通过宏DEFINE_CG_MOTIONG赋予给结构及周围的动网格由此更新结构的运动状态，待该时间步内计算收敛后进入下一时间步，由此不断循环迭代直至所监控的物理量趋于稳定。具体求解思路如图1所示。

图1 基于松耦合法求解竖向涡激振动示意图

2 涡激振动的模拟验证

为了检验本文基于松耦合方法求解竖向涡激振动数值模拟方法的正确性，选取文献[12]中的矩形断面进行涡激响应计算。其中矩形断面高为0.075 m，宽为0.3 m，为与风洞试验数据对比只考虑竖向自由度，因此将其简化为只有竖向自由度的弹簧振子系统[13]。涡激振动模拟中的设计参数均取自文献[12]，其中单位长度质量为1.362 kg，竖弯频率fn为3.905 Hz，竖弯阻尼比为0.177%。

2.1 计算区域与网格划分

为了使进口处流动能够发展完全以及出口流完全流出，从而不对流动产生影响，要保证数值模拟的阻塞率小于3%[14]，因此将计算域大小取为18B×12B的矩形，速度进口边界和上下对称边界距离矩形断面形心6B，压力出口边界距离断面形心12B，其中B为模型特征长度（B=0.3 m）。计算域以及边界条件的设置如图2所示，其中矩形断面为无滑移边界。

图2 计算域及边界条件设置

在划分网格时考虑到梁断面在运动过程中所导致的网格畸变、负体积等问题，采用分块的方式将网格分为刚性运动、动网格以及静止网格3 大区域。其中刚性运动区域距离梁断面最近，设置较密的网格，该部分网格跟随梁断面一起运动，且为了能够捕捉到气流流经主梁断面时发生的“分离”和“再附”现象，对主梁断面设置边界层网格；在动网格区域设置尺寸较大三角形网格来解决刚性域运动带来的网格质量问题；静止网格区域距离梁断面最远，对其采用渐变率较大的网格以提高计算效率，整个计算域的网格总数为46 893，其中第一层网格高度设为0.001B，近壁面网格划分如图3所示。

图3 近壁面网格划分

2.2 数值结果验证分析

采用k-ωSST湍流模型进行竖向振动瞬态绕流计算，通过UDF 控制梁体，经过充分绕流后释放梁体，分别对折算风速为4、6、8、8.5、9、9.5、10、12、14、16 共计10 个风速工况进行竖向单自由度的涡激振动计算，由于篇幅所限部分折算风速下的位移时程计算结果如图4所示。

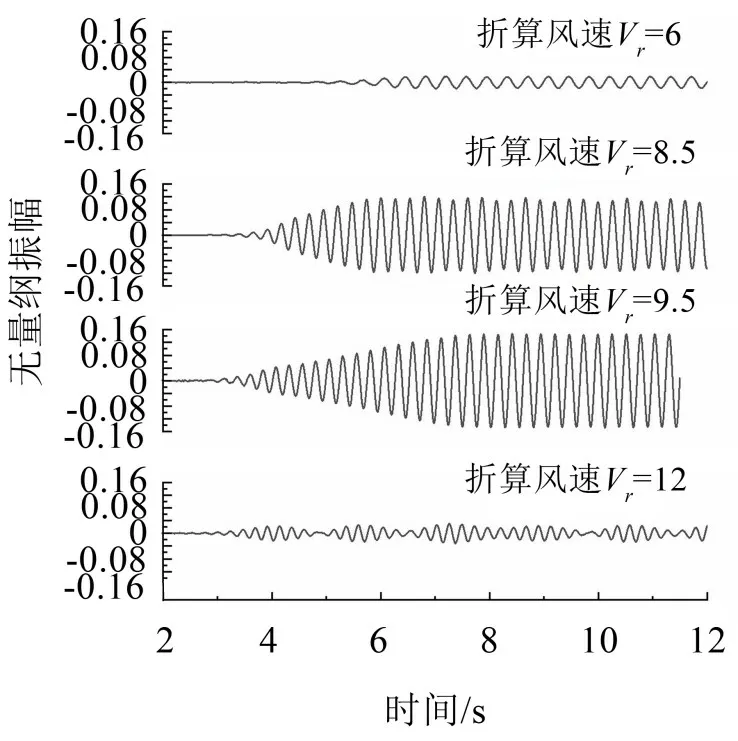
图4 不同折算风速下矩形断面位移时程曲线

由图4可知矩形断面在不同折算风速下的振动幅值差别很大，在Vr=6时振幅较小，在Vr=9.5时振幅达到最大，当风速增加到Vr=12 时振幅又减小，可见涡激振动时的风速在6～12之间。

图5所示为无量纲振幅随折减风速变化的折线图，从图中可以看出本文模拟结果中除涡振结束时的振幅有一定差异外，起振风速、最大振幅以及风速“锁定区间”同文献试验数据吻合度较高；图6所示为漩涡脱落频率与结构固有频率比（fs/fn）随折减风速变化的折线图，从图中可以看风速在6～12 之间时的fs/fn值在1.0附近，此时漩涡脱落频被结构频率“捕获”。以上结果验证了本文求解竖向涡激振动问题数值模拟方法的可靠性，该方法可用于后续的分析。

图5 无量纲振幅随折减风速的变化曲线

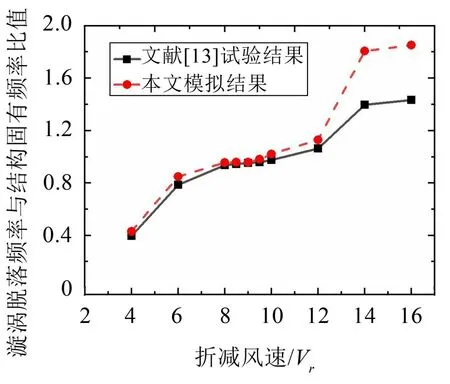
图6 频率比随折减风速的变化曲线

3 汉江大桥涡激振动模拟

3.1 有限元模型建立及动力特性计算

某拟建汉江大桥桥型为双塔双索面组合梁斜拉桥，主桥立面采用对称布置，主梁采用半漂浮体系。全桥的跨径布置为（50+112）m+370 m+（112+50）m，主桥长度为694 m，主跨跨度为370 m，边跨设置1个辅助墩和1个过渡墩，边跨跨度为162 m，边中跨比为0.437。桥面全幅宽28.3 m，桥面双向横坡的坡率为2%，π形主梁标准断面如图7所示。

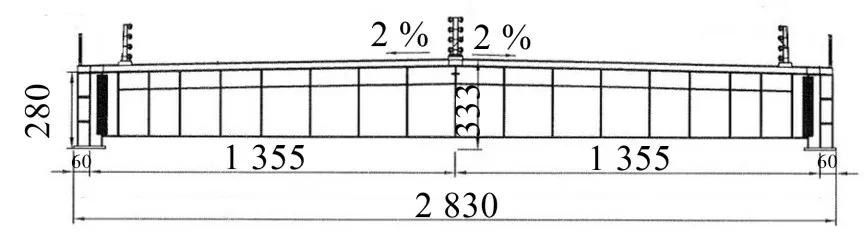
图7 π形主梁标准横断面

建立该斜拉桥有限元动力模型的工作借助软件ANSYS来完成。主梁采用单脊梁模式模拟，其中主梁、桥塔和桥墩采用BEAM188 梁单元，斜拉索采用LINK8 杆单元，二期与检修车道等附属设施采用MASS21质量点单元，全桥有限元模型如图8所示。

图8 汉江大桥有限元动力模型

表1中给出了桥梁竖弯、扭转的1阶自振频率以及对应的等效质量等参数，与表1所对应的振型图如图9所示。

图9 汉江大桥振型图

表1 动力特性计算结果

3.2 单自由度竖向涡激振动模拟

对于涡激振动，文献[15]中表明当扭弯基频比大于1.4时难以发生弯扭耦合振动的情况，这时两种涡振形式相互独立。根据表1可知文中汉江大桥的扭弯基频比为1.52，两者基频相差较大，且根据涡激振动的特点可知竖弯涡振会先于扭转涡振发生，因此本文针对竖向自由度涡振进行模拟。

3.2.1 计算域及网格划分

模拟时对主梁进行一定简化，暂不考虑护栏等附属设施，断面几何参数如表2所示，计算域的大小及边界条件的设置同图2中设置相同，网格划分方式同2.1小节中一样将网格分为刚性运动、动网格以及静止网格3大区域，具体网格划分如图10所示，第一层网格高度为0.000 2B（B为梁宽）。数值模拟相关参数设置如表2所示，其中竖弯阻尼比取为0.79%。

表2 模拟相关参数设置

图10 π梁断面网格划分

3.2.2 竖向涡激振动模拟结果

先对主梁断面进行静止绕流模拟，数值计算时采用k-ωSST双方程模型，通过Simplec算法求解耦合的速度场和压力场，时间步长取为0.001 s。通过计算来流风速为2 m/s～5 m/s范围内的St（斯托罗哈数）得到其均值为0.06，根据公式U=fnD/St估计发生最大涡振振幅时的来流风速在3.6 m/s左右，因此分别对来流风速为1.9 m/s、2.5 m/s、3.1 m/s、3.3 m/s、3.5 m/s、3.7 m/s、4.0 m/s、4.3 m/s、4.9 m/s的9个工况在0°风攻角下进行涡激响应计算。限于篇幅，本文只给出了涡振起振振幅、较大振幅、最大振幅和振幅开始减小时所对应风速下的位移时程曲线以及FFT（Fast Fourier Transform）变化频谱曲线，如图11至图14所示。

图11 来流风速为2.5 m/s时的计算结果

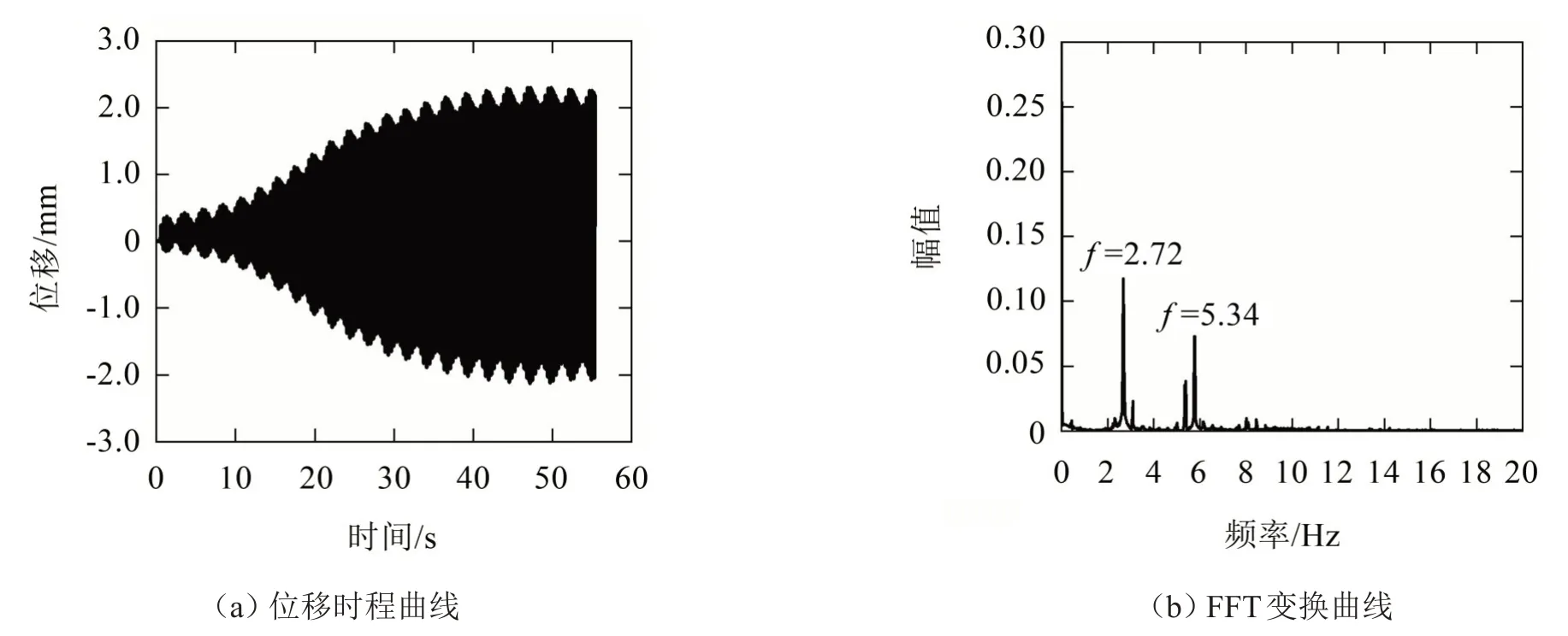
图12 来流风速为3.3 m/s时的计算结果

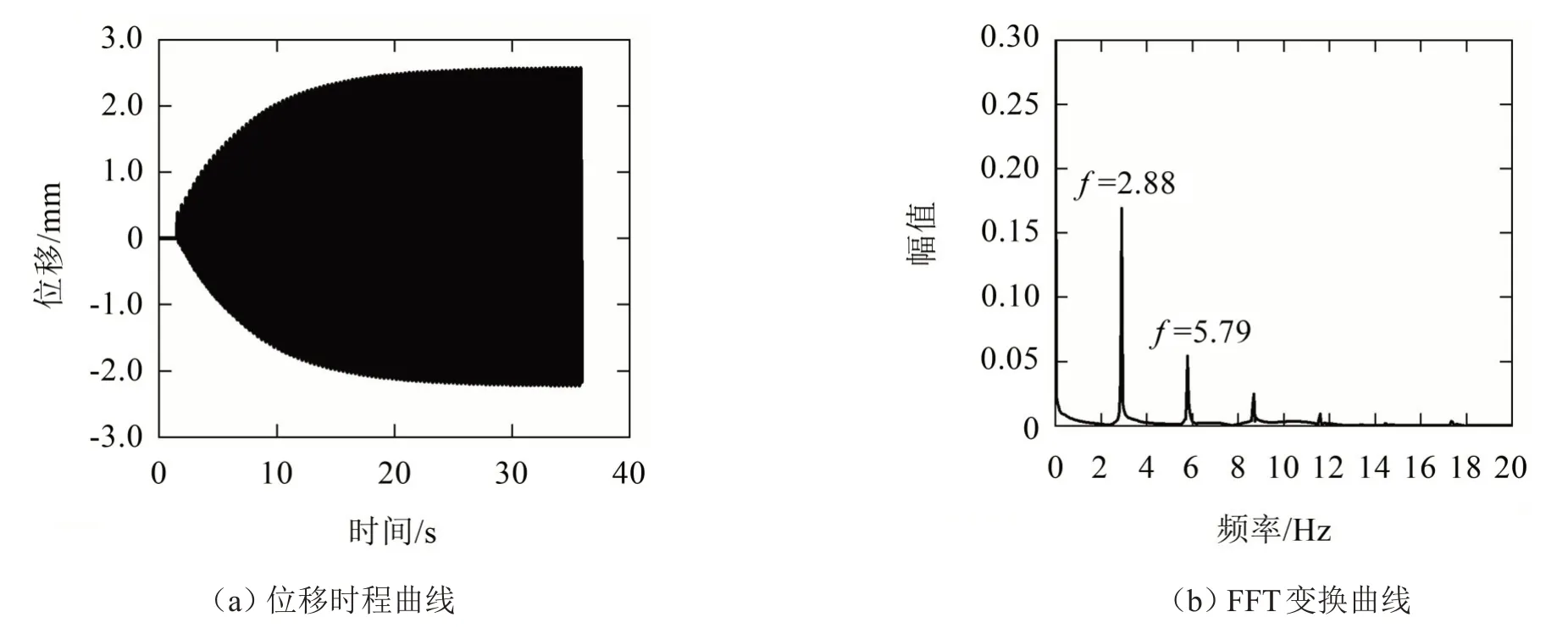
图13 来流风速为3.7 m/s时的计算结果

如图11至图14所示，在不同风速下π梁断面涡激振动幅值变化很大，在来流风速为2.5 m/s时振幅很小，对应梁断面的旋涡脱落频率（卓越频率）为2.09 Hz，此时还未被结构自振频率捕获；当来流风速增大为3.3 m/s 时，梁断面振幅迅速增大，涡脱频率接近结构自振频率，此时发生“锁定现象”；当来流风速进一步增大到3.7 m/s时涡激振幅达到最大值，此时涡脱频率与结构竖频基本一致；当风速增大至4.0 m/s 时梁断面的旋涡脱落频率继续增大，振幅回落到较小值，“锁定现象”消失。

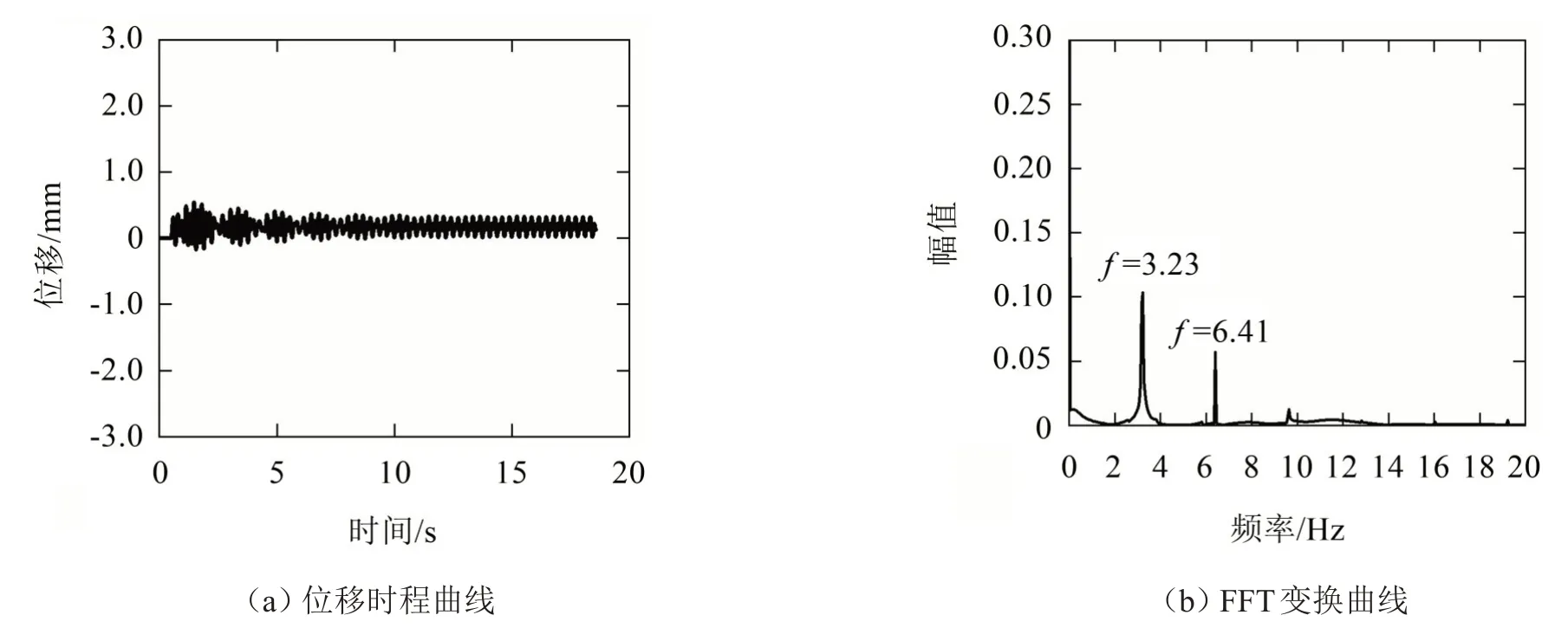
图14 来流风速为4.0 m/s时的计算结果

图15至图16分别为梁断面在1/45 缩尺下振幅随风速变化的折线图和旋涡脱落频率随来流风速变化的折线图。

图15 振幅随风速的变化曲线

从图15中可以看出，π梁断面在2.5 m/s～4 m/s的风速范围内振幅较大，发生涡激振动现象，在来流为3.7 m/s时振动幅值最大为2.57 mm；

从图16可以看出，风速在3.0 m/s～4.0 m/s的区间内时旋涡脱落频率变化很小且接近主梁竖向固有频率，即发生了“锁定现象”。

图16 旋涡脱落频率随来流风速的变化曲线

图17为来流风速为3.7 m/s 时π 梁断面某一周期内的瞬时涡脱变化图。

图17 π梁断面瞬时涡脱演化图

从图17中可以看出，在梁的不同位置处均有不同尺度的漩涡出现且主要产生自梁前缘的上下侧以及梁后缘下侧。对于梁前缘下侧的旋涡，从图17(a)中可以看出，在初始nT时刻刚生成的旋涡准备向下游移动；在nT+1/3时刻移动至梁1/2处；在nT+2/3时刻移至梁后缘并且此时梁前缘下侧的旋涡已形成较大规模；在nT+T时刻已经脱离梁断面向右下方移动，此时梁前缘下侧的旋涡经过发展已具有足够规模又开始准备移动，至此完成一个脱落周期。对于梁前缘上侧以及后缘下侧的旋涡而言，前者在经历分离、再附后与后者形成交替出现在梁尾流区域的卡门涡脱。由以上分析可知，气流在梁迎风面发生分离后分别在梁上下侧的某些固定位置形成旋涡，旋涡不断后移至梁背，此时梁背上侧与下侧的旋涡相互合并后在梁背风面形成上下不断脱落的旋涡，从而导致主梁发生竖向的涡激振动。

4 结语

本文借助流体分析软件FLUENT，基于松耦合方法通过嵌入Newmark-β法的UDF程序，求解某拟建汉江斜拉桥π 型主梁断面的竖向涡激振动问题，得到如下结论：

（1）通过对宽高比为4 的矩形断面的涡激振动模拟，证明了采用该模拟方法求解涡激振动问题的可行性和正确性。

（2）通过对9 个风速工况下的π 型主梁进行涡激振动模拟确定了“锁定区间”，发现来流在2.5 m/s～4.0 m/s风速范围内时主梁振动幅值较大，发生“锁定现象”。

（3）根据对π 型主梁断面某一完整周期内旋涡脱落过程的分析，发现在梁背风面不断产生上下脱落的旋涡导致了π型主梁断面的竖向涡激振动。