侧钻开窗钻具组合挠性短节非线性力学模型及失效分析

朱秀星, 周伟霞, 薛宪波, 张保康, 薛世峰, 梁 凯

1中国石油大学(华东)储运与建筑工程学院 2中海油田服务股份有限公司油田生产事业部工程技术中心 3中国冶金地质总局山东正元地质勘查院

0 引言

套管开窗侧钻技术是修复老井，提高油气采收率的重要工艺。开窗BHA中，挠性短节的刚度相比开窗磨鞋、次级磨鞋、钻铤等管柱的刚度小，在钻压、斜向器侧向力、开窗磨鞋切削力的作用下，借助挠性短节的弯曲大变形来调整窗口形态。若钻压等施工参数及挠性短节型号设计不当，挠性短节易由于变形过大而发生屈服失效，严重影响开窗效果及开窗钻具的上提作业。因此，研究挠性短节非线性大变形过程及失效条件，具有重要意义。

在侧钻开窗过程中，挠性短节的力学行为是一种多重耦合的非线性大变形。挠性短节力学行为的研究可分为：静力分析和动力分析。前者侧重于解决应力和变形问题，而后者主要涉及运动特性[1-2]。目前，挠性短节力学分析的研究主要集中在挠性短节的动力学模型建立方面，程载斌[3]等人用绝对节点坐标法建立了三维井眼全井中挠性短节的多体动力学模型，研究了井口、钻头处边界以及挠性短节与井壁的接触/摩擦模型，认为该多体动力学模型能很好地表征狭长井眼内大长细比挠性短节的受力、变形和运动状态；熊长华[4]等人研制出一种新型的挠性短节，认为该新型模型组合长度短，挠性角度大，弯曲灵活，机械强度安全可靠。孙刚[5]等人也建立了SDZ-8151挠性短节的动力学仿真模型，仿真计算其悬垂的过程，研究表明，在挠性短节间隙相同的情况下，内径对挠转角的影响不大，随着挠性短节间隙的增大，挠转角也在增大，挠性短节间隙是影响挠转角度变化的主要因素。此外，也有学者研究了挠性短节在黏滑振动下的非线性运动，其中，Liu[6]等人采用空间状态分析方法建立了一个四自由度非线性动力学模型，以此来描述斜井中挠性短节的运动，研究了挠性短节与井壁之间的接触行为，定性地说明了挠性短节不同倾角对非线性运动的影响，认为挠性短节和井壁之间的接触面积增加会导致摩擦扭矩的增加，随着井斜的减小，挠性短节的粘滑和旋转运动逐渐减弱，最终转化为井筒内的纯旋转运动。在钻进过程中，挠性短节的上部受拉力，下部受压力并发生弯曲，整个挠性短节在扭矩作用下进行旋转运动。Tang[7]等人针对该现象研究粘滑振动对钻井设备和钻井效率的危害以及高频扭转冲击(HFTI)对挠性短节动力响应的影响，实例研究结果表明，高频振动对钻杆状态下的挠性短节振动影响不大，并且HFTI不会激发甚至加剧挠性短节振动。许朝辉[8]等人建立开窗过程中的铣鞋-套管相互作用模型，通过仿真计算分析开窗过程中铣鞋的力学行为、不同参数对铣鞋受力和钻速的影响。

1 挠性短节非线性力学模型

本文研究采用假设：①采用三维拟静态分析方法，以简化模型；②将挠性短节视为三维弹性梁；③井眼截面为圆形；④忽略挠性短节接头的影响[9]。

1.1 几何模型

根据现场井施工数据，建立侧钻开窗BHA的简化模型，如图1所示。其中，次级磨鞋、挠性短节和开窗磨鞋的结构尺寸及材料参数见表1。由于次级磨鞋和开窗磨鞋的刚度远大于挠性短节，因此将其作为刚体处理。

图1 挠性短节与开窗BHA力学分析模型示意图

表1 开窗BHA尺寸及材料参数表

1.2 本构模型

本文讨论的挠性短节材料为42CrMn，其屈服应力为835 MPa，屈服应变为0.004 1，采用双线性弹塑性模型，该模型的应力—应变曲线如图2所示。

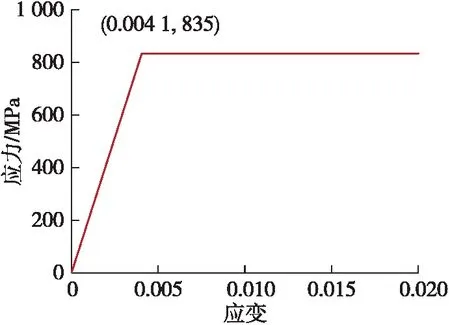
图2 45CrMn应力—应变曲线图

1.3 载荷及边界条件

1.3.1 侧向力

斜向器是一种引导工具，专门用于引导磨铣工具(例如铣锥)从套管的一侧对套管进行磨铣，从而穿透套管在套管上形成窗口，其斜面的度数范围一般为2°～4°[10]，本文所用到的斜向器的度数为2°，模型如图3(a)所示。在钻进过程中，挠性短节由于受到斜向器施加的侧向力产生横向位移，采用ANSYS数值模拟软件进行模拟时，为简化模型，用侧向力来代替斜向器对挠性短节的作用，如图3(b)所示。

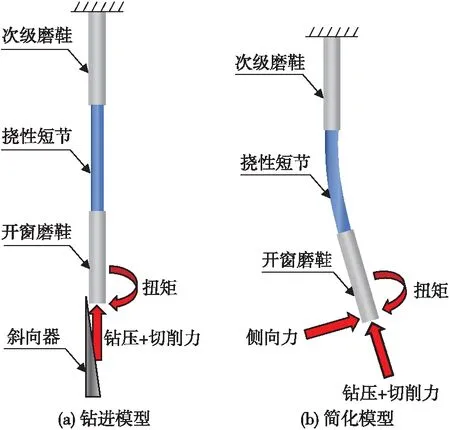
图3 开窗BHA模型图

挠性短节上端设置全约束，此时挠性短节模型简化为悬臂梁，仅受向右的集中力，可根据材料力学中计算挠曲线的方法来计算该模型中斜向器施加给开窗磨鞋的侧向力。

传统文化的传承，是任重而道远的。它是经过历史的积淀，才能流传于今；它是古老的，是神秘的，是要继续发扬下去的。但，对如今而言，也许让很多现代人觉得陌生，觉得无聊枯燥。没有网络上的世界的神通广大，没有游戏的刺激，没有电影的丰富精彩，它像是一种负担。传承，有些沉重。学一些传统诗词，也许，只是为了考试。像传统戏曲、传统乐器，越来越少的人学习，因为这些并不能给他们带来一份好的工作、好的工资。谈传统文化的传承，谈何容易？要留住“凡有井水处，皆听单田芳”的情景，是任重而道远的。

由于该模型为变截面，且为不同的材料，故在各段内截面惯性矩和弹性模量都不同，可用叠加法计算侧向力的大小。用分段刚化法(分段考虑变形)从左向右依次计算不同部分的挠度和转角，将分段考虑的变形进行叠加，即得挠性短节末端的总变形。在斜向器的作用下，挠性短节整体的变形可直接由式(1)计算出：

(1)

式中:w—挠性短节受集中力时的最大挠度，m；li—各段长度，m。

悬臂梁受集中力和集中力偶，由材料力学中最大挠度和转角的公式可得式(2):

(2)

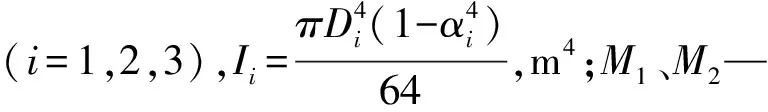
联立式(1)和式(2)，计算可得当挠性短节尺寸为表1所示时，其所受侧向力为FR=28.9 kN。

1.3.2 其它载荷

挠性短节受到的其它载荷主要包括钻压和扭矩。

2 挠性短节力学响应

2.1 数值模型

建立开窗钻具组合的数值模型，磨鞋模型采用自由网格划分，挠性短节模型采用MultiZone映射网格划分。由于本文主要研究挠性短节的力学响应，因此对该部分网格进行加密处理。

采用拟静态方法，将斜向器和套管壁对挠性短节的作用以载荷的方式代替。挠性短节在钻进过程中所受的载荷有：钻压5 t，扭矩2.5 kN·m，侧向力28.9 kN，切削力为2 701.3 N[11]。

在开窗磨鞋底面施加竖直向上的钻压和切削力，其受力图及位置如图4(a)所示；并在开窗磨鞋底面的右侧节点施加28.9 kN的侧向力，如图4(b)所示；在开窗磨鞋外边缘的位置施加2.5 kN·m的扭矩，如图4(c)所示。

图4 钻具组合受力情况

2.2 网格的收敛性分析

网格的划分精度对于有限元结果的准确性及其重要。因此，本文首先对挠性短节的网格划分进行了收敛性分析。由于在加载过程中，挠性短节的高应力区出现在与上端部分连接处，所以，只需对挠性短节中间部分网格进行细化，并通过对比不同网格精度下挠性短节连接处的最大压应力，得到最适合的网格划分密度。

通过分析可知,挠性短节中间部分网格大小为20 mm时，其最大压应力为790.24 MPa，当进一步细化挠性短节中间部分的网格为18 mm时，其最大压应力增大到了795.15 MPa，可见，挠性短节的最大压应力并未收敛。继续减小挠性短节网格尺寸到16 mm，14 mm以及6 mm时，挠性短节中间部分与上端部分连接处的最大压应力仍随之不断增大，直至挠性短节中间部分网格大小减小到5 mm时，挠性短节的最大压应力才逐渐趋于稳定。因此挠性短节网格大小控制为5 mm最为适宜。

2.3 挠性短节力学响应

加载过程中，钻具组合的最大应力为842.69 MPa(压应力)，位于挠性短节与次级磨鞋的过渡段(见图5)。这是由于受侧向力的作用，挠性短节弯曲内侧的压应力远大于弯曲外侧的拉应力，且弯曲内侧压应力由下至上依次增大，因此挠性短节与次级磨鞋之间的过渡段压应力最大。

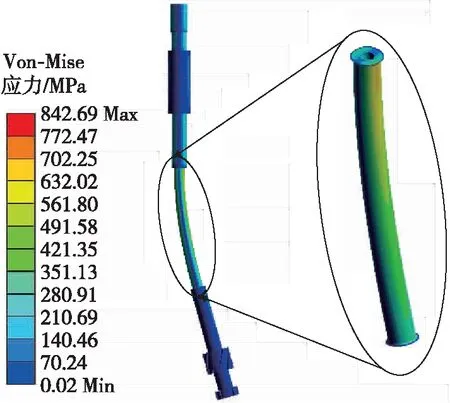
图5 挠性短节Von-Mise应力云图

3 关键参数影响规律分析

钻压、扭矩和挠性短节壁厚对挠性短节应力分布的影响，每一个影响因素包含5个取值。其中，初始模型的钻压为5 t，扭矩为2.5 kN·m，挠性短节壁厚为25.4 mm。

3.1 钻压的影响

在初始模型的基础上，分别将钻压设置为3 t、5 t、8 t、10 t和13 t，模拟获得5种工况下挠性短节的应力分布，结果如图6所示。由图6可得，当钻压分别为3 t、5 t、8 t、10 t和13 t时，挠性短节的最大压应力随着钻压的增大而依次增大。当钻压从3 t增大到13 t时，挠性短节最大压应力由838.33 MPa增大到860.13 MPa，增大幅度达到2.60%。

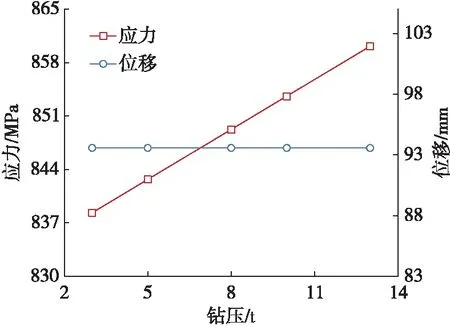
图6 钻压对挠性短节应力与位移的影响

由于钻压施加在挠性短节的轴向上，不会造成挠性短节横向偏移，因此挠性短节位移并没有发生明显变化。

3.2 扭矩的影响

改变扭矩的取值为1.5 kN·m、2.5 kN·m、5 kN·m、7.5 kN·m和10 kN·m，获得挠性短节的应力与位移分布，如图7所示。

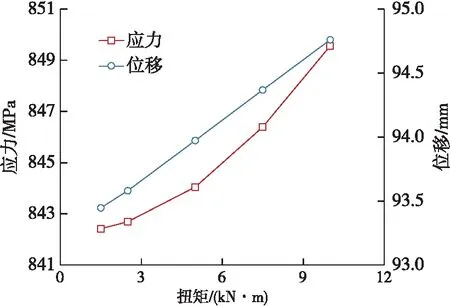
图7 扭矩对挠性短节应力与位移的影响

由图7可知，当扭矩从1.5 kN·m增大到10 kN·m，最大压应力由842.42 MPa增大到849.56 MPa，增幅仅为0.85%,挠性短节的最大压应力随着扭矩的增大而增大，但增幅很小;扭矩对挠性短节位移的影响也较小，最大位移由93.45 mm小幅增加到94.76 mm。

3.3 挠性短节壁厚度的影响

分别将挠性短节壁厚设置为10.5 mm、15.4 mm、20.4 mm、25.4 mm和30.4 mm，获得挠性短节的应力与位移分布，如图8所示。

由图8可知，最大压应力和位移均随着挠性短节壁厚的增大而减小。挠性短节壁厚对挠性短节模型的应力变化影响较大，因此当壁厚从10.4 mm增大至30.4 mm时，最大压应力由870.64 MPa减小到804.04 MPa，减幅达到7.65%。

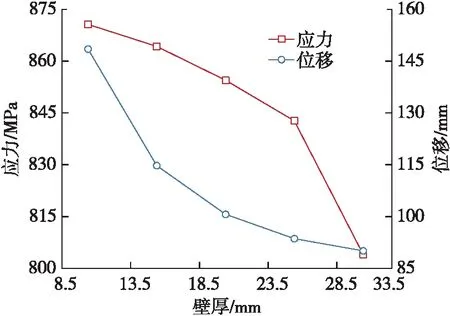
图8 挠性短节壁厚对应力与位移的影响

壁厚增大时挠性短节的抗变形能力增强，因此其位移变化量明显，当壁厚从10.4 mm增大至30.4 mm时，开窗磨鞋位移由148.50 mm减小到90.08 mm，减幅为39.34%。

3.4 极限载荷分析

基于以上方法，对侧钻开窗过程中3种常用型号挠性短节的极限载荷进行分析。当斜向器斜面度数为2°时，根据式(1)和式(2)，计算出不同型号挠性短节在受到斜向器作用时的侧向力，并以钻压和扭矩为影响因素，采用单一变量原则分析挠性短节的极限钻压和极限扭矩，结果如表2所示。该结果为侧钻开窗施工过程中钻压及扭矩的设计提供了重要的参考。

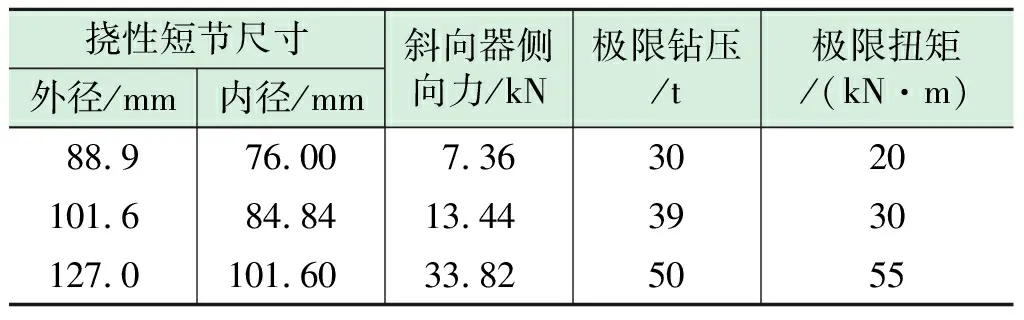
表2 不同型号挠性短节的极限载荷表

4 结论

本文应用有限元软件ANSYS Workbench数值分析了挠性短节在钻进过程中的受力状态及关键参数的影响规律，得到如下结论：

(1)挠性短节压应力极值出现在挠性短节与次级磨鞋的过渡位置，由于侧向力的作用，挠性短节弯曲内侧压应力远大于外侧的拉应力，且内侧压应力由下至上依次增大。

(2)在钻进过程中，挠性短节壁厚对开窗挠性短节的应力影响最大，扭矩影响最小。当壁厚从10.4 mm增大至30.4 mm时，最大压应力由870.64 MPa减小到804.04 MPa，减幅达到7.65%；当扭矩从1.5 kN·m增大到6 kN·m，最大压应力由842.42 MPa增大到849.56 MPa，增幅仅为0.85%。

(3)对于Ø88.9 mm挠性短节，施工过程中建议的极限钻压为30 t，极限扭矩为20 kN·m；Ø101.6 mm挠性短节建议的极限钻压为39 t，极限扭矩为30 kN·m；Ø127 mm挠性短节建议的极限钻压为50 t，极限扭矩为55 kN·m。