基于混合有限差分格式的非线性奇异摄动问题的最大范数的后验误差估计

包小兵， 刘利斌， 梁治芳

(1. 池州学院大数据与人工智能学院，安徽 池州 247000;2. 南宁师范大学数学与统计学院，广西 南宁 530299)

0 引言

众所周知，奇异摄动问题广泛存在于自然科学和工程技术的各个领域，如Navier-Stokes 方程、油藏模拟、量子力学、最优控制等。这类问题所对应的微分方程的高阶导数项包含正的摄动参数。一般情况下，这类问题很难求出精确解，尤其是非线性的问题。因此，研究奇异摄动问题的数值方法显得非常的重要。

基于此，本文考虑如下带参数的一阶非线性奇异摄动问题

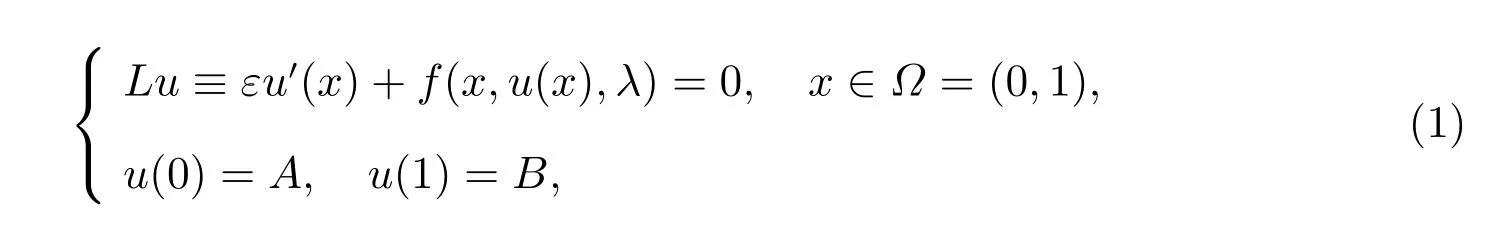
其中0＜ε ≪1，λ是待求的参数，A和B是已知的常数。假设函数f(x，u(x)，λ)∈C1(Ω×R2)，且存在常数α、b*、m1、M1，使得

由条件(2)和(3)可知，问题(1)存在唯一解。当ε →0 时，问题(1)的解在x= 0 处存在边界层。

近十多年来，带参数的奇异摄动问题数值方法的研究引起了许多学者的兴趣。Amiraliyev 和Duru[1]在Shishkin 网格上构造了问题(1)的有限差分方法，并证明了离散格式是几乎一阶收敛。接着，Amiraliyev 等[2]进一步证明了在Bakhvalov 网格下的有限差分法是一阶收敛的。Cen[3]针对问题(1)，在Shishkin 网格下提出了一种混合的有限差分格式，并证明了离散格式是几乎二阶收敛的。Wang 等[4]提出了一种数值求解问题(1)的高精度的重心有理谱方法，但是没有给出任何理论分析。在文献[5]中，Kudu 将问题(1)的边界条件改成了积分边界条件，并在Bakhvalov 网格下证明了有限差分离散格式是一阶一致收敛的。显然，上述大部分方法属于奇异摄动问题的层适应网格方法。该方法构造简单，且比较容易分析其收敛性，但是该方法要求给出解的先验信息。

相比之下，自适应移动网格方法可广泛应用于工程应用中所涉及的有边界层的奇异摄动问题的求解。例如，段献葆等[6]考虑了流体力学中典型的Navier-Stokes 方程，对求解区域进行有限元剖分，进而构建移动网格算法进行求解，但作者并未给出理论分析。最近，Das[7]利用向后的欧拉公式对问题(1)进行了离散，并利用多项式插值的误差估计，给出了离散解的最大范数的后验误差估计，并设计了相应的网格生成算法。基于有限差分方法，Shakti 和Mohapatra 在文献[8—9]中讨论了问题(1)的自适应移动网格算法，利用外推技术及解的导数估计，证明了半离散格式下的自适应移动网格算法是二阶收敛的。刘利斌和方虹淋[10]在文献[7]的基础上系统讨论了问题(1)的自适应移动网格算法，证明了在经典的弧长控制函数下，半离散格式是一阶收敛的。同时，利用多项式插值的误差估计，给出了基于全离散格式的后验误差估计的自适应网格算法。考虑到文献[8—9]仅仅给出了半离散格式下自适应移动网格算法的收敛性，而文献[10]的收敛阶只有一阶，本文受文献[3]的启发，将在任意网格下给出问题(1)的混合有限差分格式，并证明离散格式的稳定性。然后，利用多项式插值技术，推出了混合差分格式的后验误差估计，并以此设计了相应的网格生成算法。

注1 在本文中，C表示与ε和网格大小N无关的任意常数，在不同的位置可以表示不同的数值。

1 预备知识

为了能更好的构造数值方法，首先给出精确解及其导数的边界和渐近性分析。然后，构造了在非均匀网格上的离散格式。最后，得到了离散解的稳定性分析。

2 后验误差估计

最后，由引理2 可得(23)式。

3 自适应网格生成算法

众所周知，后验误差估计对奇异摄动问题自适应网格算法的设计起到至关重要的作用。近年来，许多学者利用有限差分或有限元方法，给出了奇异摄动问题的后验误差估计及相应的网格生成算法[11–14]。一般情况下，自适应网格算法的基本思想是构造合适的后验误差估计

4 数值实验

为了验证本文构造的后验误差估计及相应的自适应网格算法的有效性，我们考虑如下带参数的非线性奇异摄动问题

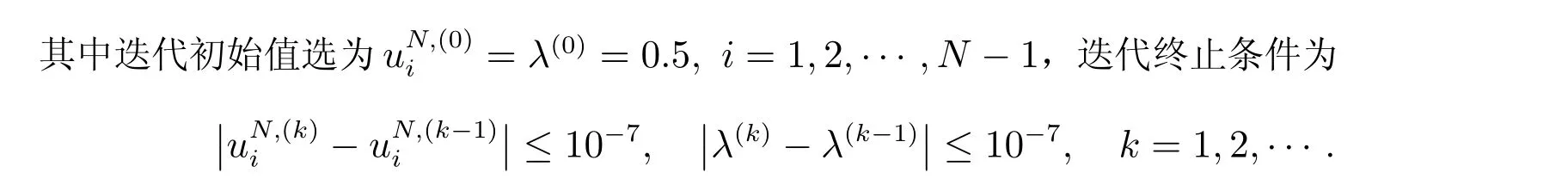
根据文献[3]所构造的Shishkin 网格及差分格式，分别对应于上述ε和N的取值，计算得到相应的误差和收敛阶。结果表明，在此网格下，对于不同的ε参数值，计算结果完全相同，因而只在表2 中列出了ε=10-j(j=4，5，6，7)时的计算结果。从表1 和表2 的数值结果可以看出，本文提出的自适应网格方法的收敛阶明显高于Shishkin 网格方法的收敛阶，同时也验证了理论结果。

表1 自适应移动网格算法的数值结果

续表

表2 Shishkin 网格算法的数值结果

此外，为了进一步展示自适应网格的迭代生成过程，当ε= 10-6，N= 64 时，图1 画出了网格的移动过程(自下而上)。同时，图2 也给出了当ε=10-6，N=64 时，问题(34)的数值解的变化曲线。从图1 和图2 可以明显看出，问题(34)的解在x= 0 点处存在边界层。

图1 网格迭代过程

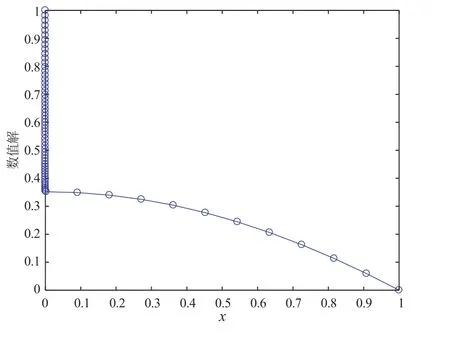
图2 数值解的曲线图

5 结论

基于混合有限差分格式，本文系统讨论了一类带参数的一阶非线性奇异摄动问题的自适应移动网格算法。利用离散格式的稳定性和多项式插值，构造了一个具有二阶精度的最大范数的后验误差估计，并设计了相应的网格算法。值得一提的是，本文所给出的后验误差估计的构造思想及相应的网格生成算法可以进一步推广到其他一阶奇异摄动问题的数值模拟。