单摆系统的多时滞控制与特征根分析

赵东霞， 范东霞， 王婷婷， 毛 莉

(中北大学理学院，太原 030051)

0 引言

单摆是一个具有深厚物理背景的典型非线性系统，基于单摆的应用已经有很多，例如，在机械振动、汽车工程等领域都具有重要的应用价值。越来越多的国内外专家学者和工程技术人员对单摆系统的镇定和控制问题产生了兴趣。例如，文献[1]采用Lyapunov 函数方法建立了无阻尼单摆系统的稳定性。文献[2]提出了一种自适应滑模控制器，建立了分数阶单摆系统在有限时间内的稳定性和收敛性。文献[3]研究了单摆的混沌运动，给出了周期性外力作用下的单摆系统的动力学分析。另一方面，研究表明，简单的位置反馈往往不能取得受控系统的满意结果，甚至不能使受控系统达到稳定。因而，伴随着时滞系统稳定性分析的不断深入，时滞反馈控制器在单摆系统的镇定问题上得到了广泛应用，通过调整反馈参数及时滞值使得系统达到渐近稳定甚至指数稳定，取得了一系列的研究成果[4–8]。文献[9]从近似计算和数值仿真的角度阐述了位置反馈和时滞位置反馈控制器的优越性。文献[10]采用特征根分析方法，建立了单摆系统的稳定性与系统参数及时滞值之间的充要条件，分别得到了与时滞相关和与时滞无关的稳定性结论。文献[11]研究了位于小车上的倒立摆系统的时滞控制器设计，建立了与时滞相关的稳定性结论。文献[12]针对有阻尼的单摆系统，分别采用Lyapunov 函数方法和Lyapunov 矩阵方法得到了系统稳定时参数所满足的充分性条件。

受上述文献启发，本文采用位置反馈和时滞位置反馈控制器去镇定一类单摆系统，并且将控制器本身具有时滞这一实际因素考虑了进去。此时，目标系统变为一个双时滞系统，该系统稳定的参数充分性条件以及特征值的渐近表达式在已有文献中尚未可见。本文第1 部分，主要是设计控制器建立数学模型，第2 部分，致力于建立与时滞相关和与时滞无关的稳定性结论，第3 部分，主要是分析特征根的重数并导出当特征值的实部趋于负无穷大时特征值的渐近表达式，第4 部分，利用Matlab 数学软件进行数值仿真用以佐证结论的有效性。

1 系统描述

众所周知，系统(4)是局部渐近稳定的当且仅当线性化系统(5)是渐近稳定的(对于线性系统而言，局部稳定和全局稳定是等价的)，亦当且仅当系统(5)的特征方程的所有根具有负实部。本文致力于建立线性化系统(5)的稳定性以及特征值的渐近表达式，尤其是时滞τ2的出现对系统稳定性的影响。

2 稳定性分析

于是，随着时滞τ2的微小增加，应用解析函数的零点重数之和关于参数的连续依赖性定理[13]可得如下结论。

引理2 当τ2＞0 且充分靠近0 时，特征方程(6)的所有根均具有负实部，当且仅当参数满足(8)式。

随着时滞τ2的进一步增加，稳定性发生切换，当且仅当零点出现在虚轴上或穿越虚轴。于是，不妨设λ=iω(ω ＞0)为特征方程(6)的纯虚根，则

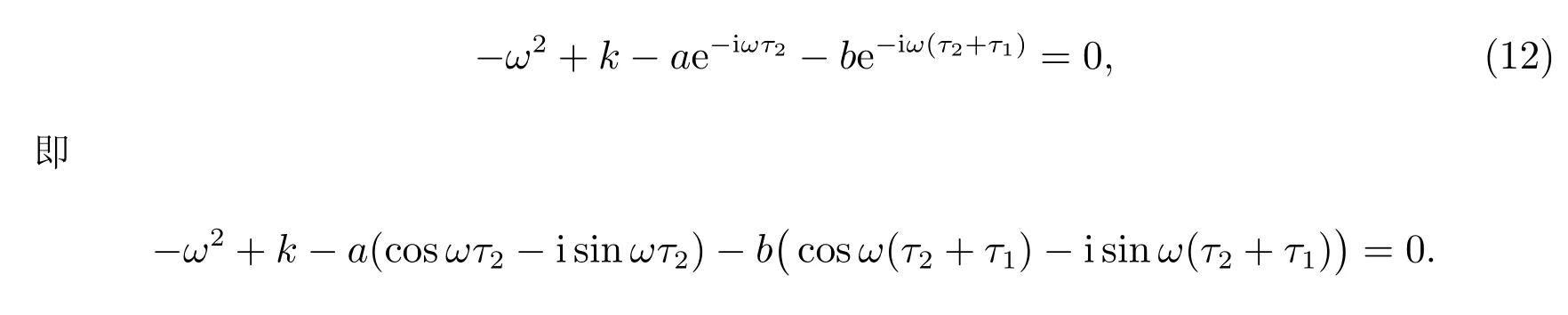
3 特征值分析

4 数值仿真

在这一部分，利用Matlab 数学软件对时滞单摆系统(4)的稳定性进行数值模拟。

例1 在系统(4)中，取L= 1 m，g= 9.8 m/s2，τ1= 0.5 s，a= 8，b= 0.5。一方面，容易验证这些参数满足条件(8)。另外，计算可得，方程(16)无根(见图1)。于是，由定理1 可得，系统(4)的零解渐近稳定，如图2 所示，其中τ2= 0.4 s，初值条件取为θ(t)=0.5，θ′(t)=0，t ∈(－0.9，0)。

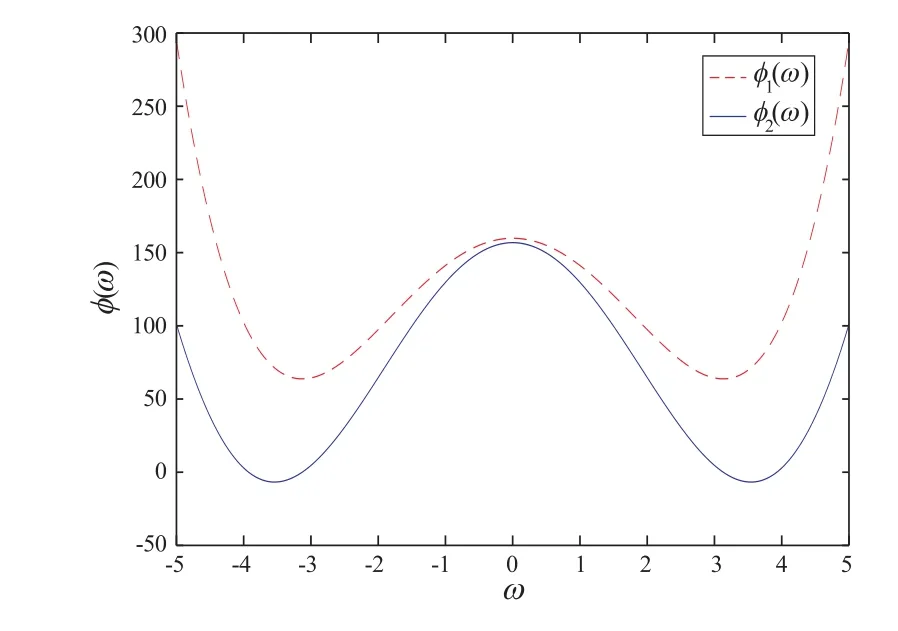
图1 方程(16)无实根

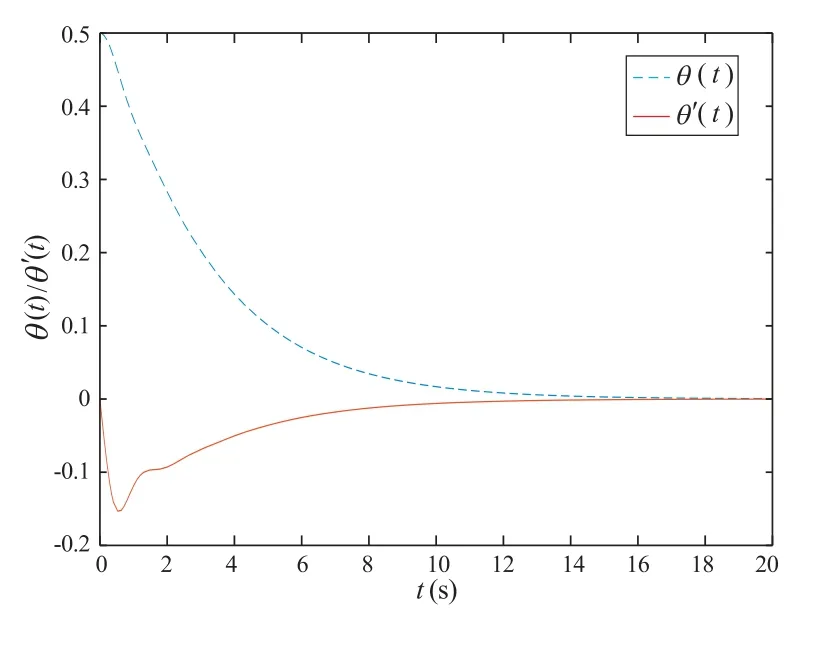
图2 a=8， b=0.5， τ1 =0.5 s， τ2 =0.4 s 时，系统(5)的状态的收敛性

例2 在系统(4)中，取L= 1 m，g= 9.8 m/s2，τ1= 0.3 s，τ2= 0.2 s，a= 1，b=1.5。一方面，容易验证这些参数满足条件(8)。另外，结合(16)式、(17)式和(18)式，计算可得τ02= 1.066＞τ2。于是，由定理2 可得，系统(4)的零解渐近稳定，如图3 和图4 所示，其中初值条件取为θ(t)=0.5，θ′(t)=0，t ∈(－0.5，0)。

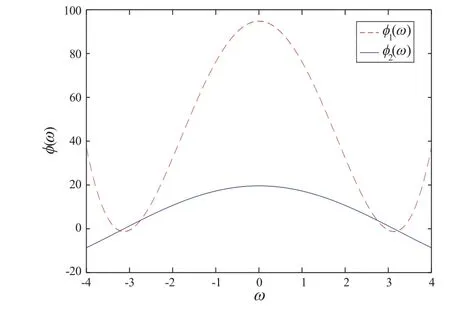
图3 方程(16)有实根

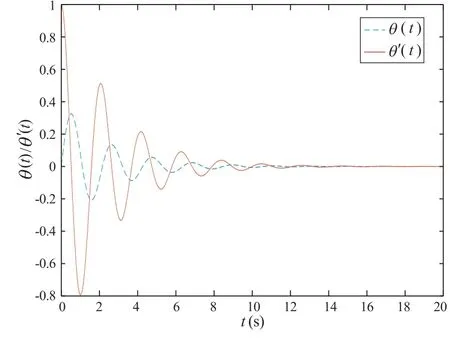
图4 a=1， b=1.5， τ1 =0.3 s， τ2 =0.2 s 时，系统(5)的状态的收敛性

5 结论与讨论

本文采用位置反馈和时滞位置反馈控制器(即PDP 控制器)去镇定一类单摆系统，并且将控制器本身具有时滞这一实际因素考虑了进去。此时，目标系统变为一个双时滞系统，本文首先采用特征根分析方法考查含有两个时滞的线性化单摆系统的稳定性，建立了系统参数及两个时滞值与系统稳定性之间的关系，得到了与时滞相关和与时滞无关的稳定性结论。进而，本文还分析了特征根的代数重数以及当特征值的实部趋于负无穷大时特征值的渐近表达式。最后，通过Matlab 数值仿真验证了结论的有效性。本文的宗旨是用时滞控制器镇定一类非稳定二阶常微分方程(ODE)系统，对于n阶ODE 系统的多时滞控制问题进行类似的研究将是我们接下来要做的工作。