基于梯度差的声速剖面自适应分层算法

马 茜,段 毅,徐 冬

(1.西咸新区轨道交通发展有限公司,陕西 西咸新区 712000;2.南瑞集团有限公司(国网电力科学研究院有限公司)，江苏 南京 211000; 3.国电南瑞科技股份有限公司,江苏 南京 211061)

0 引 言

声波在水中传播衰减小，是迄今为止唯一能够在水中远距离传播的信息载体，决定了水下通信的性能。水下声学定位系统通过距离、角度等参数进行定位。其中距离是声速与时间的乘积，这样计算的前提是假设声速在水中传播时保持不变，而实际情况是水中声速随环境变化，水中声线也不是一条直线。如果直接以一个固定的声速值代入计算就会引入较大的误差。在水下定位过程中，声速误差是定位过程中最主要的误差。

水下声学定位需要对声线进行修正处理[1-2]。修正弯曲声线能够减少误差，因此国内外专家学者提出了如有效声速法、查表法、等效声速剖面法和声线跟踪法[3-9]等多种方法。其中，声线跟踪法基于声速分层假设，把复杂的声速垂直分布剖面近似视为由多层恒定声速或恒定声速梯度的声速层构成[3]。利用海洋声速剖面数据，采用分层计算、合计累加的思想对弯曲声线进行补偿[4]。

用等间隔分层或人工筛选等简单分层方法重构声速剖面，不能充分保留原始声速数据特征，分层不尽合理，定位精度不高，定位计算效率低。针对这个问题研究人员也提出了多种分层方法。张居成等[5]提出了一种基于等效声速剖面的自适应分层方法，用常梯度分布的声速剖面曲线代替原始声速剖面，在指定精度下自适应搜索非等间距划分的最少层数声速剖面。李圣雪等[6]提出了一种声速剖面自适应分层方法，通过曲线拟合计算曲率半径，依据曲率半径筛选声速剖面，在深海长基线定位中提高了定位效率。Xiong等[7]采用3次样条插值法重构声速剖面，在等声速声线跟踪法中效果较好，但常梯度声线跟踪法对采样间隔变化不敏感，使用常梯度声线跟踪法时声线修正效果一般。李建等[8]基于(Douglas-Peucker， D-P)算法，计算声速剖面上偏移量最大的点[4-9]作为分层点，该方法在确保定位精度的前提下对声速剖面进行精简，但选取的特征点只能够宏观上控制曲线的形态，并不能准确判别真正特征点[10]。本文针对分层数与运算量相矛盾的问题，提出一种基于梯度差的声速剖面自适应分层算法(Adaptive Division of Sound Velocity Profile Based on Gradient Difference, ADGD)。通过逐层搜索，依据声速层之间的梯度差变化情况找出声速变化的节点，能够对声速剖面数据进行合理抽取，保留信息量多的声速层，精简声速剖面，提升声线跟踪效率，实现对声速剖面的最优简化，以较少的分层数达到较高的定位精度。该算法适用于常梯度声线跟踪计算。该方法原理简单，计算简便，效果较好。

1 声线修正方法

声线跟踪法利用声速剖面数据和射线声学的Snell法则分层迭代计算声线轨迹，是一种精确的声线修正算法。常梯度声线跟踪法假设声波在水中经历多个常梯度层[11-14]，每一层声速的梯度恒定不变。在声速常梯度变化的情况下，波束在第i层内的实际传播轨迹为一个连续且对应一定曲率半径ri的圆弧段[15]，层i内声线的水平位移xi为:

(1)

式(1)中θi为第i层声线的入射角。波束在该层经历的弧段长度为:

si=ri(θi-θi+1)

(2)

则经历该段的时间为ti为：

(3)

常梯度法声线跟踪示意图如图1所示。其中，Z轴为深度，X轴为水平位移长度。θi为第i层声线与水平面的夹角，Δzi为第i层水层深度，xi为第i层声线的水平位移，gi为第i层声速梯度，ri为第i层曲率半径。

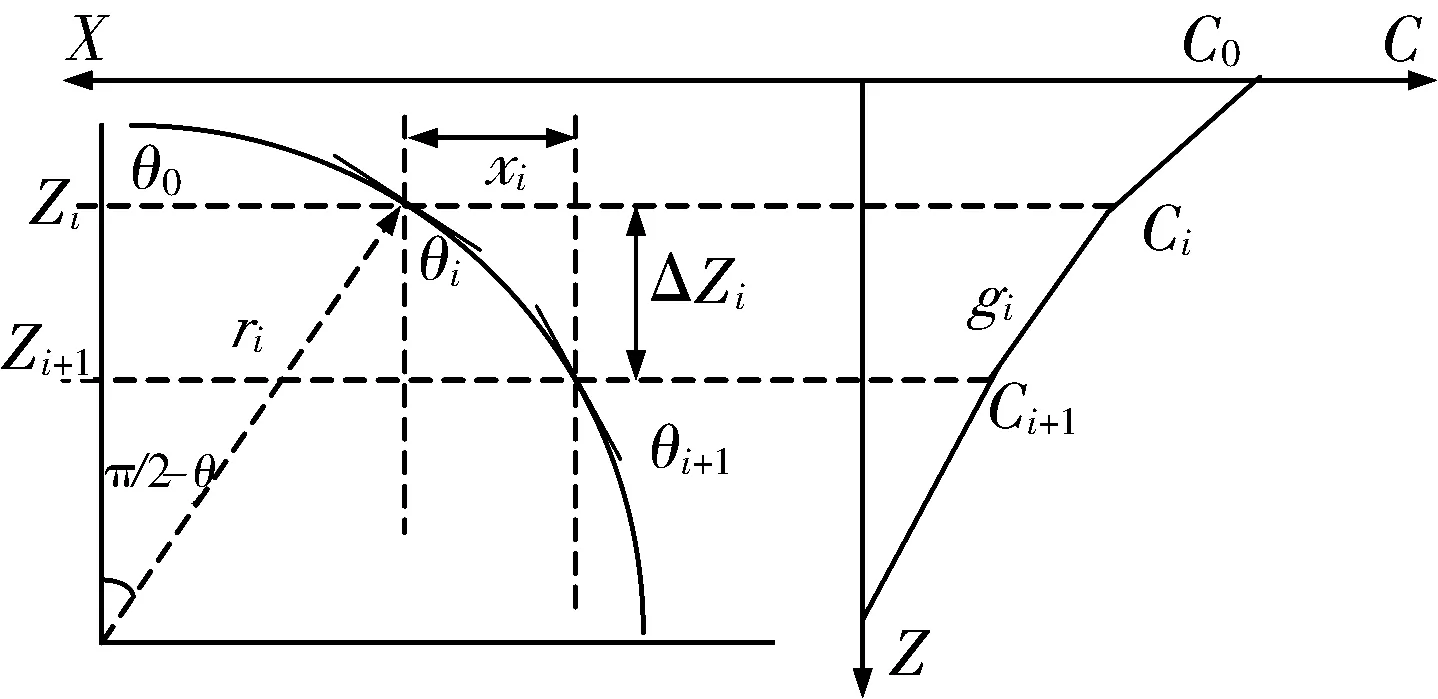
图1 分层常梯度声线跟踪示意图

2 ADGD算法

海水中的声速可以用声速剖面来描述[16]，声速剖面反映声速沿深度方向的变化规律[17]。声速剖面[18-23]的分层结果对定位结果也有一定影响，合理的分层结果可以在一定程度上降低后续声线跟踪的计算量并且不降低其定位精度。

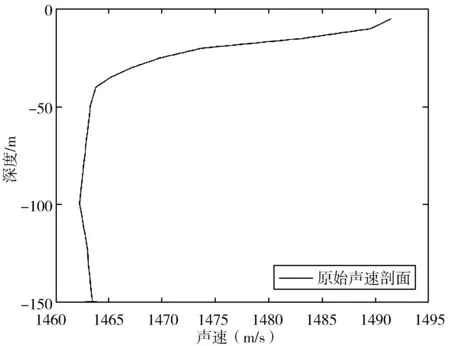
原始声速剖面如图2所示。声速梯度反映了声速的变化情况[24]，在一定深度范围内，声速梯度恒定，梯度差反映了相邻2个水层间声速梯度的变化程度。ADGD算法依据梯度差将声速梯度变化小于阈值的水层划分为一层，契合常梯度声线跟踪算法思想，达到简化计算的目的。梯度差R计算公式为：

图2 声速剖面曲线

(4)

式(4)中ci为该声速剖面的第i层对应的声速。zi分别为该声速剖面的第i层对应的深度。

ADGD算法原理图如图3所示。其中X轴为声线轨迹的水平位移，Z轴为深度。C轴为声速。图3中右图为声速剖面，左图为对应的声线轨迹。图3中的声速剖面每1层的梯度值恒定。其中第i声速层和第i+1声速层的梯度差较小，所以自动将这2层合并为1层。图中声速剖面曲线的虚线部分为优化后的声速剖面曲线。可以看出优化后的声速剖面相对于原声速剖面误差较小，且更为精简。可以有效提高声线跟踪效率。

图3 ADGD算法原理图

ADGD算法流程图如图4。具体步骤如下：

图4 ADGD算法计算流程图

步骤1计算每1层的声速梯度值。

步骤2从第2层开始计算其与前1层的梯度差R，并设置阈值G。

步骤3如果小于阈值则合并声速层后不用后移1层，直接继续选取2个连续声速层，如果大于阈值则后移一层并选取2个连续声速层。

步骤4对梯度差计算所选取的梯度值的细节阐述，不在流程图中具体体现。如果在合并过程中前1层是经过合并后的声速层，则计算该层与前1层合并前的原始声速层之间的梯度差

步骤5判断当前是否为最后1个声速层。若是则输出优化后的声速剖面并结束计算。否则返回步骤3继续计算，直至将整个声速剖面全部优化完成。

3 仿真实验

为验证ADGD算法的普适性，本文分别选取4个不同深度不同变化特性具有代表性的声速剖面，对每1个声速剖面分别设置合适的阈值进行仿真实验。声速剖面自适应分层图如图5所示，自适应分层数据对比见表1。图5(a)采用典型深海声速剖面数据，用SSP1表示。图5(b)采用海南陵水冬季正梯度声速剖面数据，用SSP2表示。图5(c)采用湖北黄烨港冬季正梯度声速剖面数据，用SSP3表示。图5(d)采用千岛湖负梯度声速剖面数据，用SSP4表示。图5中横轴为声速，单位为m/s。纵轴为深度，单位为m，线条表示原始声速剖面曲线，上三角符号为通过优化算法选取的节点。

(a) 原始剖面

表1 不同声速剖面下的简化情况表

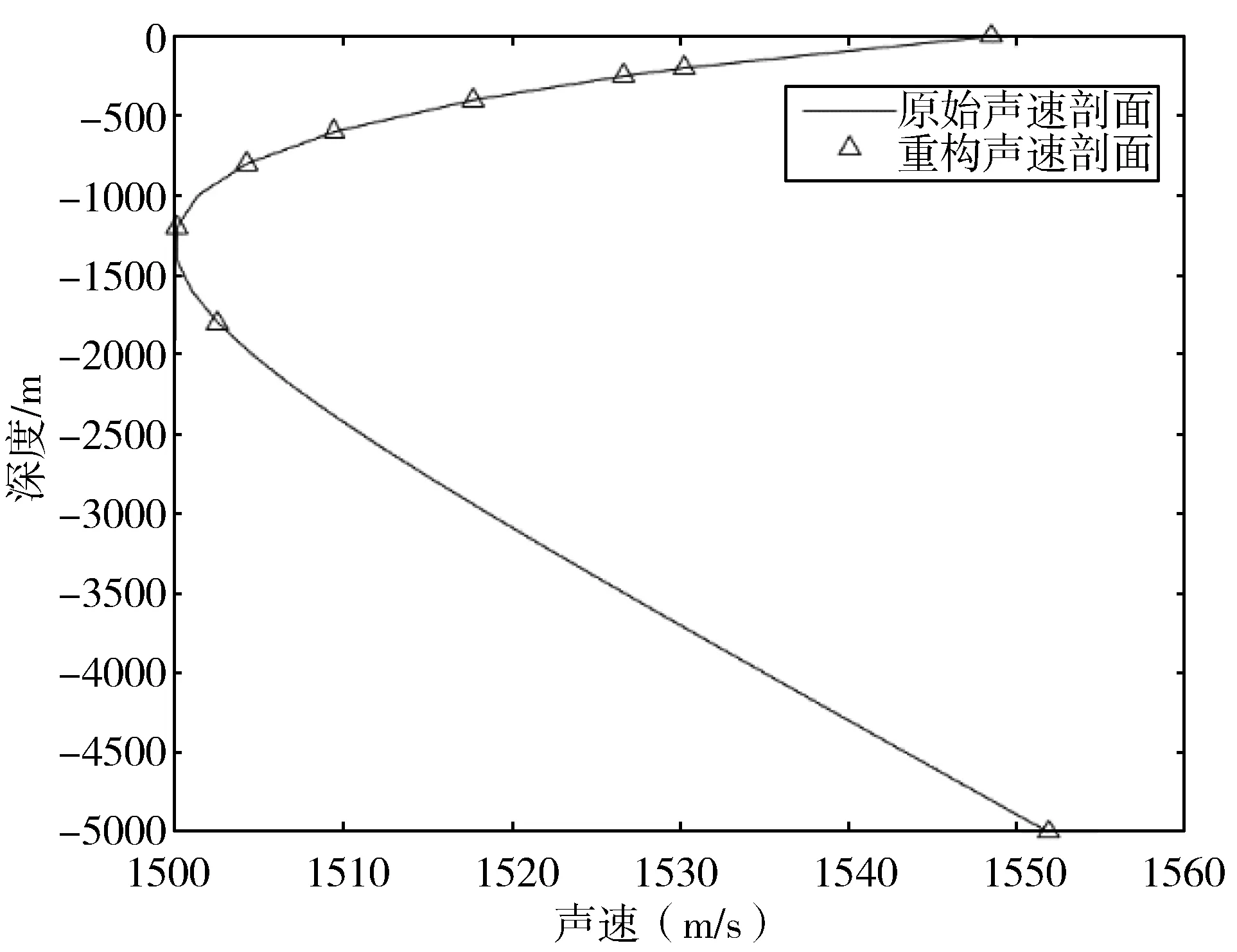
(a) SSP1

相关系数可以反映变量之间的线性相关程度，用r(cpre,cnew)表示，本文通过相关系数公式定量表示了原始声速剖面与精简声速剖面的相关程度。相关系数r(cpre,cnew)的取值在0到1之间，r(cpre,cnew)越大则相关程度越大，相关系数r(cpre,cnew)接近1时，通常认为原始声速剖面与简化后声速剖面线性相关程度较好。本文的相关系数公式定义如式(5)：

(5)

式(5)中cov(cpre,cnew)为原始声速剖面与精简声速剖面的协方差。Var[cpre]和Var[cnew]分别为原始声速剖面与简化后声速剖面的方差。

为衡量该声速剖面自适应分层算法对降低声速剖面冗余数据点的能力，设定精简率ξ来表示自适应算法在声速剖面数据中择优选点的效果，并通过式(6)定义：

(6)

式(6)中Npre表示声速剖面修正之前的数据节点数。Nafter表示声速剖面修正后的节点数。

均方误差MSE可以评估数据的变化程度。MSE的值越小，描述实验数据的预测模型的准确度越高。对于MSE的定义如式(7)：

(7)

式(7)中N为数据点的个数，obsi为声速剖面第i层的声速值，prei为经自适应分层后声速剖面第i层的声速值。

表1中原始分层数表示声速剖面原始层数，优化后分层数表示自适应分层计算后分层数。

由于声速剖面特性各不相同所以不同声速剖面之间精简率与相关系数变化情况并不一致。从图5和表1中可以看到，对于4个完全不同的声速剖面，优化后声速剖面的精简率最低为57%，最高可达90%，均取得了不同程度上的简化。从上面4个实验结果可见每个声速剖面的相关系数都超过0.99，说明本文算法在各种声速剖面中都能保留原声速剖面的特性，具有较好的择优选点能力。此外，通过上面4组实验可以发现，本文算法对于数据量较大的声速剖面精简率较高，说明本文算法更适用于精简数据量庞大的声速剖面。以上实验都证明了ADGD算法做到在降低声线跟踪的计算量的同时也能保证声速剖面的准确性，适用于不同的声速剖面，具有较好地用于工程应用方面。

为了验证ADGD算法在超短基线定位中的定位精度[25-26]，本文采用某湖一个深150 m的实测负梯度声速剖面数据(见图2)进行仿真实验。其中，声速剖面采样间隔为5 m，有30个采样点。

使用ADGD算法并不断变化阈值优化声速剖面，通过超短基线定位仿真定位结果。相关系数、精简率、均方误差、定位误差(见表2)。声速剖面自适应分层结果如图6所示。图6(b)、图6(c)、图6(d)为优化后的声速剖面。优化后的数据点使用上三角符号标识。

表2 ADGD算法不同阈值时分层定位结果

D-P算法是一种声速剖面自适应分层算法，通常用于对高度复杂的多线段进行简化。等间隔分层算法是一种声线跟踪中常用的分层算法，通过沿深度方向的等间隔划分重构声速剖面。ADMV(Adaptive Division Based on Minimum Variance)算法是基于最小方差的声速剖面自适应分层算法，是一种采用最小二乘法拟合曲线，利用最小方差搜寻最佳切分点的声速剖面自适应分层算法，在长基线定位中比D-P算法定位误差略小[27]。为了验证ADGD的性能，对D-P算法、ADMV算法、等间隔分层算法和ADGD算法进行了定位精度的对比。由于定位时间取决于声速剖面所划分的层数，层数越多，定位消耗的时间就越长，定位效率越低。所以用声速剖面层数为x轴，定位误差为y轴，对比4种算法在相同定位效率时的定位误差，如图7所示。

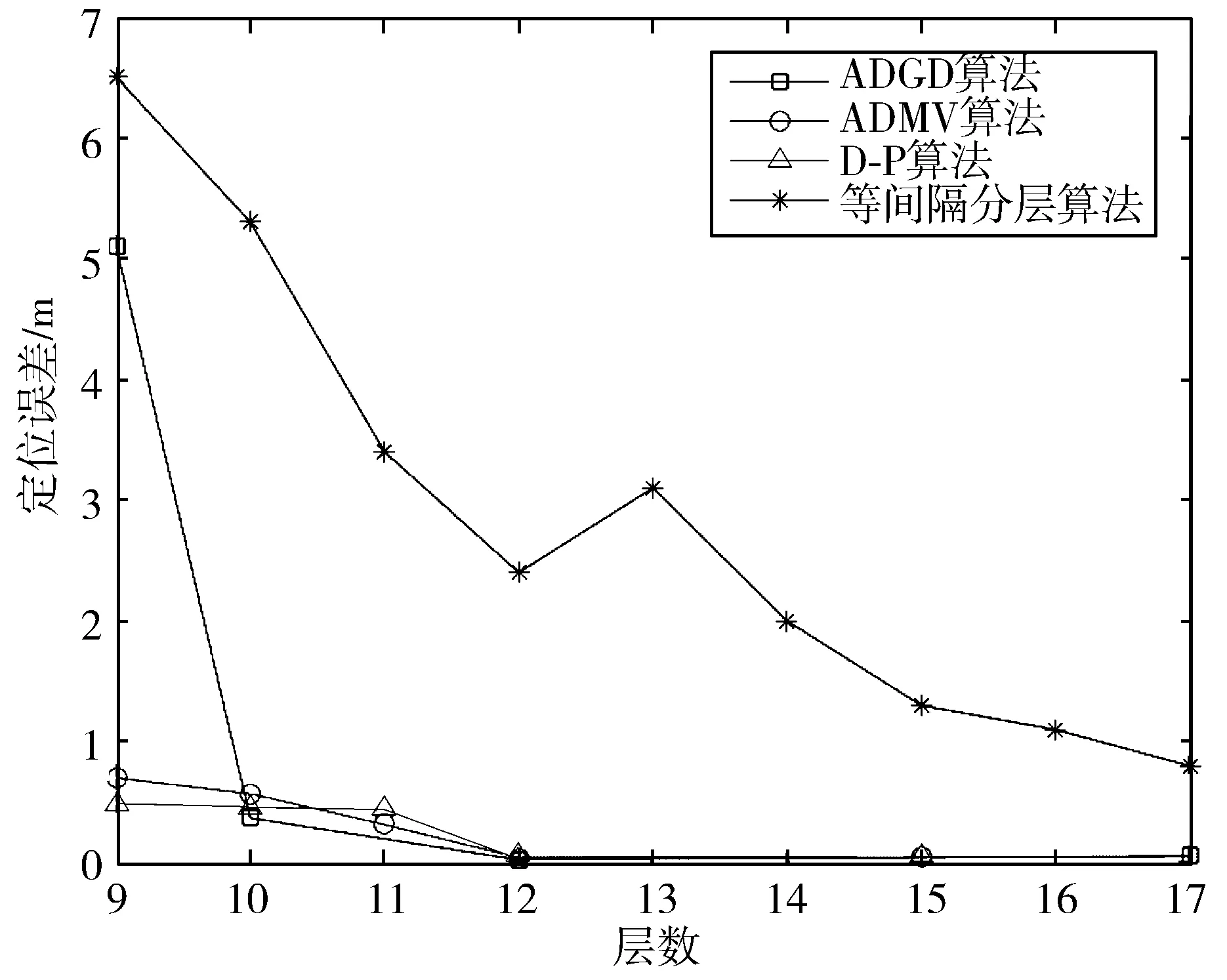
图7 不同算法声速剖面分层数与定位误差的关系

图7中层数从9层增加到17层时，4种分层算法都是随着层数增加，定位误差降低。由于等间隔分层法分层方式不能反映声速剖面的特征，误差最大。ADMV算法与D-P算法误差相当。当层数从10到12层时，ADMV算法与D-P算法定位误差均高于ADGD算法。大于12层以后，除等间隔分层法以外的3种算法误差均接近与0。

4 结束语

本文针对水下定位中定位精度和计算效率的矛盾，提出的ADGD算法利用常梯度声线跟踪方法对每个声速层声速梯度恒定的假设计算声速梯度差，并依据阈值逐层合并声速剖面，从而实现声速剖面自适应分层。实现了对声速剖面中进行冗余数据筛除及特征数据选取。

ADGD算法的计算效率和定位精度成反比例变化关系，所以本算法在对声速剖面进行优化时，需要设置适合的阈值。随着阈值的增大，优化后声速剖面的数据量也逐渐越少，与原声速剖面的偏差也越大。反之阈值设置越小，对于原始声速剖面的精简效果越差，越贴合原始声速剖面。所以阈值的选取应在合理的范围内。当阈值选取较小时，对于声速变化缓慢的区域比较敏感；当阈值选取较大时，对声速变化剧烈的区域较为敏感，所以ADGD算法通常在声速梯度变化剧烈的水层选取的分层节点更为密集。该过程不需要人工干预，实现了自动化搜索分层与定位。选取合适阈值时，与D-P算法对比获得了更小的定位误差。