一种改进的求解柔性作业车间调度问题的灰狼算法
2022-08-18田云娜赵彦霖
田云娜,田 园,刘 雪,赵彦霖
(延安大学数学与计算机科学学院,陕西 延安 716000)
0 引 言
在制造系统中,生产调度是其中非常重要的一个环节,会直接影响企业的生产经济效益。经典的生产调度问题主要包括流水车间调度问题和作业车间调度问题。柔性作业车间调度问题(Flexible Job-shop Scheduling Problem, FJSP)是对经典作业车间调度问题的扩展,它是一类复杂的组合优化问题,已被证明属于NP-hard问题,主要特点是工件的加工路径具有柔性,这大大增加了问题的灵活性和复杂度。相对于作业车间调度问题,FJSP具有更广泛的实际应用和更高的求解难度,因而其一经提出便引起了高度关注。
在现有的关于FJSP的研究中,此类问题的求解方法主要可以分为精确算法、启发式算法和智能优化算法3大类[1]。
精确算法指能够求出问题最优解的算法,主要包括分支定界法、割平面法、动态规划等。虽然它能够为调度找到全局最优解,但它需要对问题进行统一建模。而对于复杂多变的生产调度问题,单一的数学模型并不能考虑到所有因素,并且当问题规模和计算复杂度不断增加时,寻求最优解的时间将会呈指数级上升。启发式算法被用于解决精确算法难以在短时间内求解的问题。启发式规则是一类常见的启发式方法,它凭借计算复杂度低、可实时调度等特点在生产调度问题中被广泛使用[2]。然而启发式规则对于调度环境和目标的依赖性较强,并不存在某一规则能在所有环境和评价标准下都表现出良好的性能。同时,启发式规则寻优能力较差,在复杂的加工环境下无法保证解的质量[3]。
智能优化算法是一类随机搜索进化算法,这类算法利用学习策略和已知信息搜索解,通过不断迭代优化生成问题的解。经典的智能优化算法包括遗传算法[4]、进化策略[5]、遗传规划[6]、差分进化等进化算法和蚁群优化算法[7]、粒子群优化算法、人工蜂群算法[8]、飞蛾扑火算法[9]等群智能算法。由于算法原理简单、易于实现等特点,智能优化算法被很多学者应用于求解复杂的、大规模的组合优化问题。
本文拟解决的FJSP就是一类复杂离散组合优化问题,这类问题规模大,计算复杂度高,很难通过精确算法求得全局最优值,群智能算法的出现为解决这类问题提供了新思路。董蓉等人[10]将遗传算法和蚁群算法相结合提出一种混合算法求解FJSP;贾兆红等人[11]提出了一种基于粒子群优化和禁忌搜索的混合算法用以求解多目标FJSP;李俊萱等人[12]提出了一种混合量子粒子群算法用以求解加工时间不确定的FJSP;郑小操等人[13]提出了一种改进人工蜂群算法用以求解模糊FJSP;Caldeira等人[14]针对3个目标的多目标柔性作业车间调度问题,提出了一种离散Jaya算法。
灰狼算法(Grey Wolf Optimizer, GWO)是由Mirjalili等人[15]根据灰狼捕食原理提出的一种新的群智能算法。由于GWO算法原理简单,需要调整的参数少,且搜索能力强,收敛速度快,因而被应用于生产调度问题的求解。姜天华[16]提出了一种混合灰狼优化算法用以求解以优化最大完工时间为目标的FJSP;Lu等[17]提出了一种多目标离散灰狼优化求解焊接车间调度问题;Komaki等[18]设计了一种混合多目标灰狼优化算法来解决多目标动态焊接调度问题。
本文基于经典的灰狼算法,在迭代过程中加入新的优化策略,提出一种改进的灰狼算法(IGWO)以求解FJSP。算法采用基于权值的编码方式,将工序选择不同机器进行加工的概率用权值表示,以此实现连续编码的离散化;然后通过随机游走策略加强局部搜索能力,并采用尾部淘汰策略进行种群更新;最后,在基准算例上进行仿真实验,通过与其他算法进行对比,验证IGWO求解FJSP的有效性。
1 问题模型
本文优化目标为最大完工时间,接下来对所求问题建立数学模型并求解。
1.1 问题描述
设n个工件在m台机器上进行加工,每个工件有k道工序,每道工序可在若干台机器上加工,工件内工序加工顺序及工序在不同机器上加工的时间一定。调度的目标是为工序选择合适的机器,并确定各机器上工序的加工顺序,使某些指标尽可能达到最优。此外,还需满足以下假设:
1)所有工件和机器在0时刻均处于就绪状态。
2)同一时刻一台机器只能加工一道工序。
3)同一道工序在同一时刻只能在一台机器上进行加工且只能加工一次。
4)工件一旦开始加工就不允许中断。
5)仅考虑同一工件内工序加工的先后次序约束,不同工件间工序优先级相同。
6)忽略机器的准备时间,且不考虑机器故障。
1.2 变量定义
变量定义如下:
J={Ji|1≤i≤n},表示工件集;
M={Mk|1≤k≤m},表示机器集;
Oi={Oij|1≤j≤ni},表示工件Ji的工序集;
Mij表示工序Oij的可选机器集合;
Pijk表示工序Oij在机器k上的加工时间;
L表示一个无穷大的正数;
Ci表示工件Ji的完工时间;
Cmax表示最大完工时间;
sijk表示Oij在k上的开始加工时间;
fijk表示Oij在k上的完工时间;
1.3 数学模型
本文以最小化最大完工时间为优化目标,目标函数的数学表达式如公式(1)所示。
minCmax=min max(Ci), 1≤i≤n
(1)
根据实际生产中的问题特性,本文约束条件描述如下:
Cmax≥Ci, ∀i
(2)
spqk≥fijk-(1-yijpqk)×L
(3)
(4)
(5)
Ci≥0, ∀i
(6)
sijk≥0,fijk≥0, ∀i,j,k
(7)
其中,约束式(2)定义了最大完工时间;约束式(3)表示同一时刻一台机器只能加工一个工件的一道工序;约束式(4)表示加工次序约束,即同一工件内只有前一道工序完成后才能开始加工下一道工序;约束式(5)表示每道工序会且仅会分配给一台机器;约束式(6)和式(7)限制了决策变量的取值范围。
2 改进灰狼算法
2.1 经典灰狼优化算法
灰狼算法是通过模拟自然界中灰狼种群的社会等级和捕食行为而提出的一种群智能算法。在算法中,将狼群个体依照适应度值由大到小排序,排在前3的个体分别定义为α、β和δ,其余个体均定义为ω,以此模仿灰狼的社会等级。为模拟灰狼狩猎过程,假定α、β和δ能够获得潜在猎物的位置。每次迭代开始前,先找出α、β和δ,并保存好位置信息,其余个体均以此为依据更新自己的位置,按此方式迭代直至猎物被捕获。上述过程可用以下公式表示:
(8)
(9)
(10)
A=2a·r1-a
(11)
C=2r2
(12)
(13)
其中,X是表示灰狼个体位置的向量,A和C是系数向量,可以根据公式(11)和(12)得到,r1和r2是[0,1]上的随机向量,t表示当前迭代次数,T表示最大迭代次数。公式(8)计算个体到α、β、δ的距离,公式(9)确定个体的移动方向,a在迭代过程中根据公式(13)从2递减到0。
2.2 编码解码
2.2.1 编码机制
FJSP包含机器分配和工序排序2个子问题,本文采用基于权值的方式,对2个子问题分别进行编码。
1)机器分配。
对于具有柔性的工件,每道工序选择不同的机器进行加工时所对应的权值是不同的,在对一道工序进行机器分配时,权值较大的机器被选中的概率较高。部分示例编码如表1所示。

表1 机器分配编码
表1表示一个有3道工序的工件,每道工序对应不同的机器有相应的权值,例如,第1道工序O11选择机器1加工的权值为0.1,选择机器2加工的权值为0.5,O11不能在机器3上加工,依此类推。
2)工序排序。
机器分配结束后,对于被分配到同一台机器的工序而言,权值大的被优先加工的概率较高。部分示例编码如表2所示。
表2列举了M1和M5这2台机器缓冲池中待加工工序,以及每道工序对应的权值。其中O11、O22和O31被分配到M1上,O12、O21和O32被分配到M5上。每道工序的权值将作为解码时的选择依据。
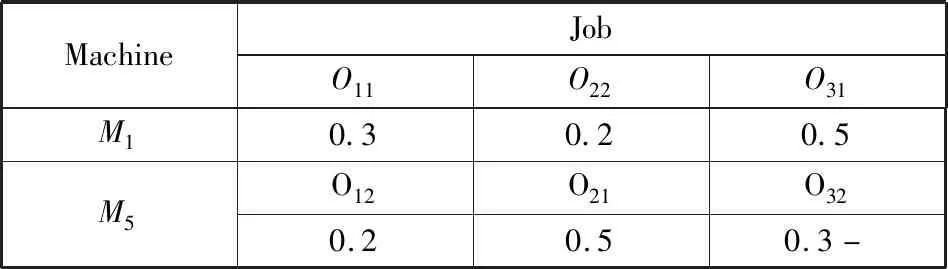
表2 工序排序编码
2.2.2 解码机制
1)机器分配。
机器分配部分解码过程如图1所示。机器分配部分,得到的解形如[[1,2,0],[3,1,0]],其中0、1、2等数字为位置索引,O11的可选机器集MO11={M1,M2,M4,M5},于是O11选择的加工机器为MO11[1]=M2,以此方式解码,可得到机器分配方案。

图1 机器分配解码过程
2)工序排序。
工序排序部分解码过程如图2所示。

图2 工序排序解码过程
图2中,(0,(0,2))表示工件1的第3道工序在机器1上加工,(1,(0,0))表示工件1的第1道工序在机器2上加工,按照此方法解码,最终可得到一个完整的调度方案。
2.3 随机游走
随机游走能够扩大人工狼的搜索范围,在一定程度上增加种群多样性,以达到增强搜索广度、加强算法局部搜索能力的目的。
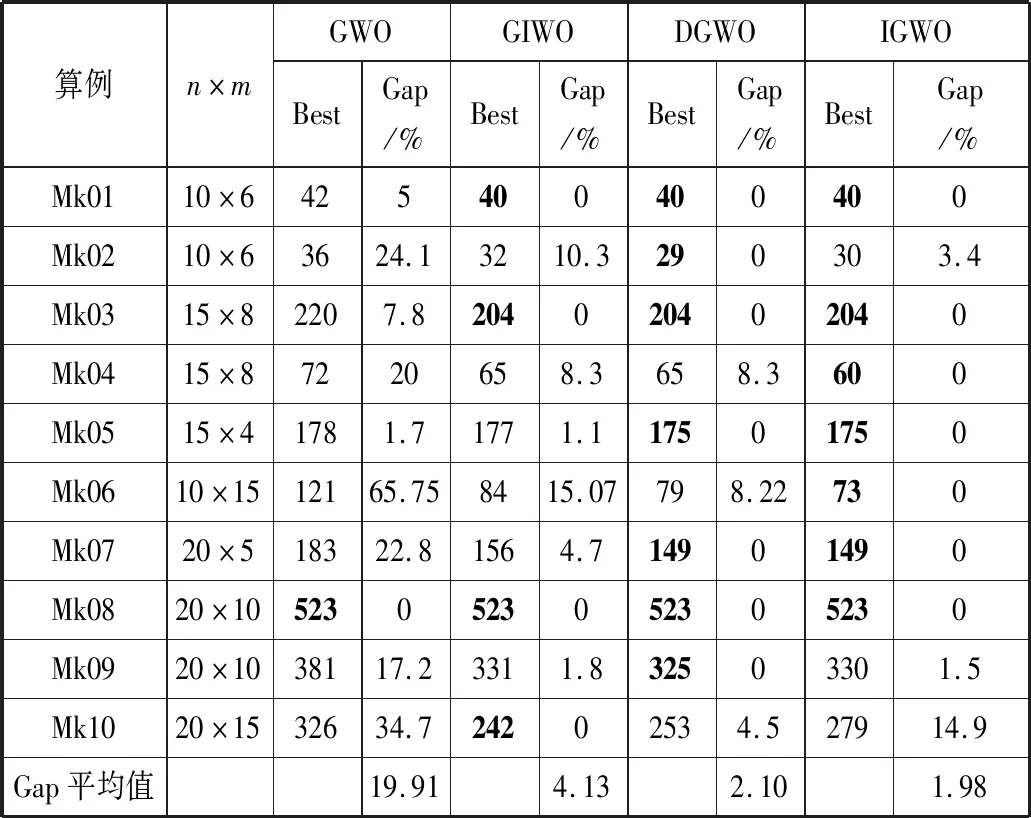
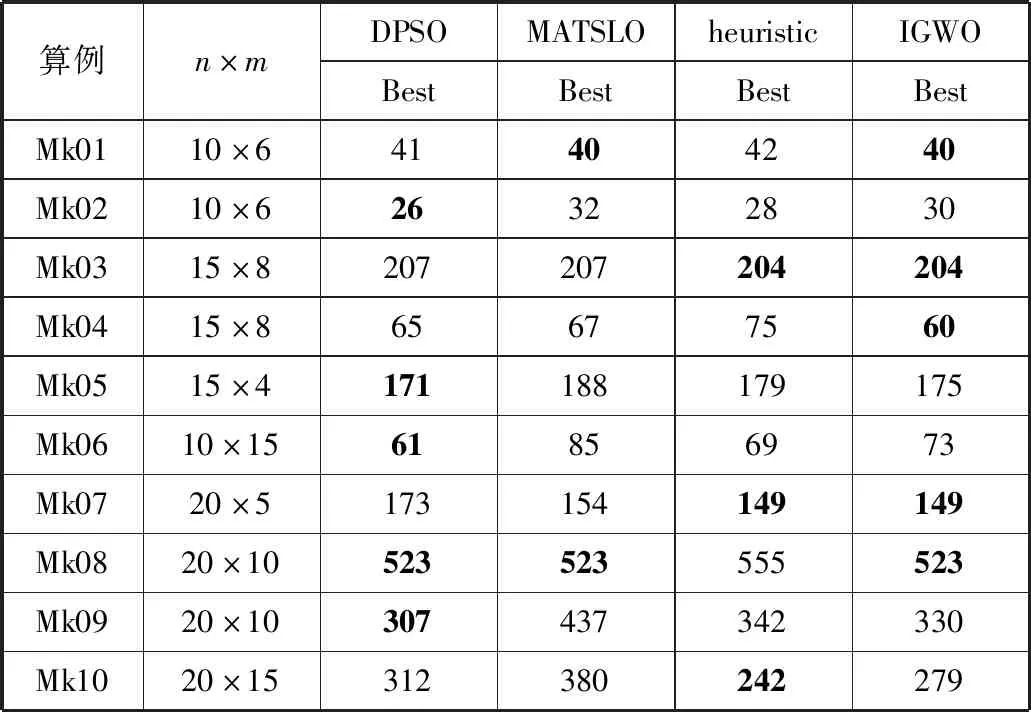
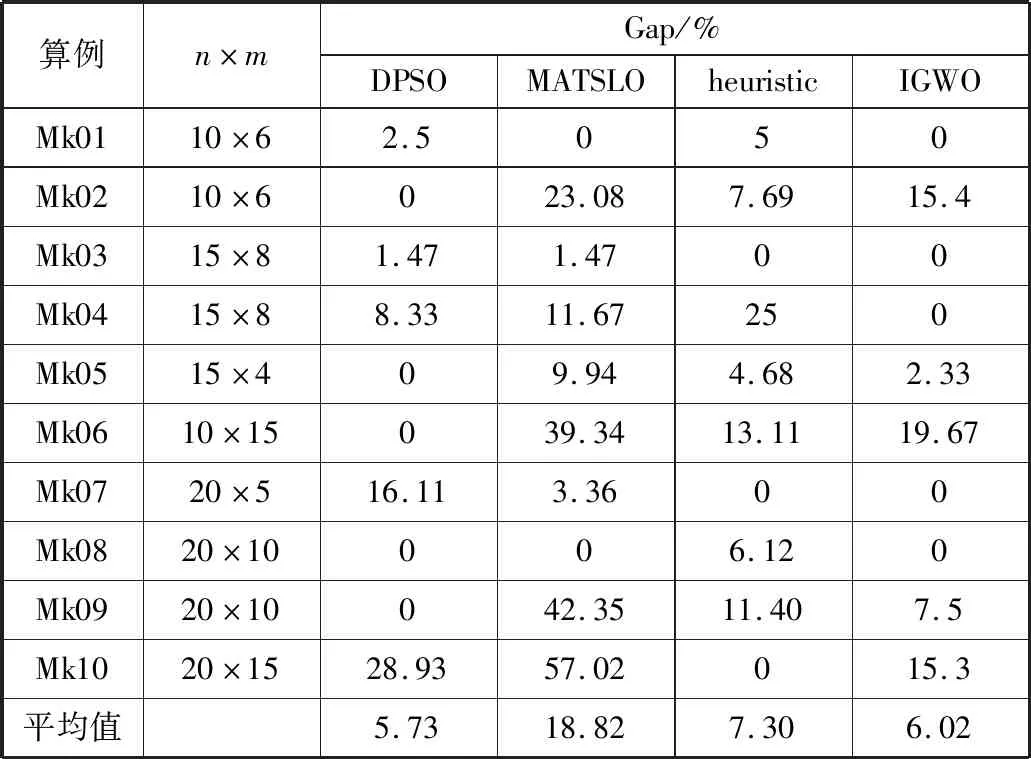
令种群中除α、β、δ以外的Nr匹人工狼进行以自我为中心的局部搜索,Nr取[ns·wr],ns为种群大小,ωr为随机游走率。记人工狼i向第p(p=1,2,…,h)个方向游走前后的适应度值分别为Yi和Yip,当Yip 将人工狼i向第p(p=1,2,…,h)个方向游走定义为:在人工狼i的编码Xi=[xi1,xi2,…,xin]中随机选取2个值xip和xiq,对其进行交换操作,并将此操作执行h次。交换操作如图3所示。 图3 交换操作 人工狼i的编码Xi=[0.1,0.2,0.5,0.3,0.2,0.2,0.1,0.3],当i向方向p游走时,随机选取2个值xip=0.2和xiq=0.3,对xip和xiq执行交换操作,于是Xi的编码变为[0.1,0.3,0.5,0.3,0.2,0.2,0.1,0.2]。 种群更新采用尾部淘汰策略。在种群更新的过程中,一轮迭代结束后,淘汰适应度值差的R匹狼,为使狼群规模不发生变化,再随机产生R匹人工狼。由于R的取值会影响算法的寻优性能,R过小不利于维护种群的多样性,R过大会导致算法接近于随机搜索。这里参考吴虎胜等人[19]的论文,令R的取值为[ns/(β+1),ns/β]之间的随机整数,ns为种群大小,β为种群更新比例因子。 IGWO算法的具体步骤如下: Step1设置参数并初始化种群:设置种群大小、最大迭代次数、最大游走次数、随机游走率ωr等参数;创建初始种群,随机产生一批初始解。 Step2计算适应度值,寻找α、β、δ:计算每匹人工狼的适应度值,然后按照适应度值的排序选出最佳的3匹狼。 Step3随机游走:令种群中满足随机游走条件的人工狼进行以自我为中心的局部搜索。重复这一游走行为,直至某匹狼的适应度值Yi Step4包围猎物:所有狼均向α、β、δ这3匹狼的方向靠近。位置更新过程根据式(8)~式(10)进行,靠近的过程中若Yi Step5种群更新:根据式(11)和式(12)更新A、C,并按照尾部淘汰策略进行种群更新。 Step6若t>T或满足停止条件,算法结束,输出当前最优解;否则,转到Step2。 综上,IGWO算法流程图如图4所示。 图4 IGWO算法流程图 为验证所提算法的优化性能,本文进行了多组对比实验。仿真实验采用Python语言,在Win10系统下内存16 GB的i7-4790 CPU @ 3.60 GHz计算机上运行。 由于FJSP是一类经典的生产调度问题,研究者们在对此类问题进行研究时普遍选择一些通用的标准算例作为测试用例,如Brandimarte[20]和Kacem等人[21]所采用的的测试用例。这2组测试用例的规模分别是从4×5到15×10和10×6到20×15,能较好地测试算法在各规模下的有效性。鉴于实验对比公平性,本文也选取Brandimarte和Kacem测试问题对算法进行验证。 本章首先将所提算法与GWO相关算法进行比较,对算法中添加的策略的有效性进行验证,然后与其它文献中的经典算法进行比较以进一步验证所提算法的优化性能。 本文首先设置种群大小ns=100,最大迭代次数T=300,并选取Brandimarte实例中的Mk01(10×6)、Mk07(20×5)、Mk09(20×10)以及Mk10(20×15)这4个实例分别进行多次实验,再选取部分实验结果绘制出每个实例的收敛曲线,由图5可知,迭代均可在前150次以内完成,因此设置最大迭代次数T=200。 然后,分别设置群大小为20、50、100、150以及200,以Mk07与Mk10为例对每个参数值独立运行15次后取平均值,得到图6,可以看出,当ns>100时,结果没有明显的变化,因此设置种群大小ns=100。此外,IGWO算法还有3个关键参数:游走次数Trmax、游走步长μ和游走率ωr。 (a) Mk01收敛曲线 (a) Mk07 由于不同的参数设置对算法性能有不同影响,因此,本文以Brandimarte实例中的Mk06算例为测试用例,通过正交试验设计方法进行参数设置实验。实验参考谢锐强等人[22]的方法,利用正交试验表L9(33)进行实验,算法中3个关键参数的选取参考现有狼群算法。表3为实验中3个参数不同的水平值设置。 表3 参数水平 参数实验中将每个参数组合独立运行15次,所选正交组数以及对应的适应度平均值(AVG)汇总统计见表4。 表4 正交表和AVG统计 为了查看每个参数在不同水平下的总体表现,取每个水平值下3个组合的平均值进行衡量,表5展示了3个关键参数的响应值。根据表5得到每个参数的影响因子水平趋势,如图7所示。 表5 各参数响应值 (a) 游走次数灵敏度分析 综合考虑算法的复杂度及搜索质量,建议的参数组合为: Trmax=5,μ=0.4,ω=0.5 本文实验验证主要分2部分进行,首先是与经典狼群和其他狼群相关算法的对比实验,然后是与其他群智能算法的对比实验。 与其他狼群算法的比较目的是出于对本文所提算法中添加的改进策略的有效性进行验证。对比对象包括经典灰狼算法(GWO)、文献[23]的DGWO算法、文献[24]的GIWO算法。算法针对不同算例分别独立运行20次后进行比较,对比结果如表6所示。 表6中Best表示算法独立运行20次获得的最佳结果,粗体表示各算法经过比较后IGWO在该算例下取到的最佳结果。Gap表示相对百分比偏差,其计算方法见公式(14)。 表6 GWO相关算法对比 (14) 其中,Best表示各算法运行20次所得的最好结果,Min表示所有算法最好结果中的最小值。 根据表6中的数据和计算结果可以看出,相较于GWO,IGWO在每个算例中都能得到比GWO更好的解;作为改进的灰狼算法,相较于DGWO和GIWO,10个标准算例中,GIWO取得了4个最好值,DGWO和IGWO各取得了7个最好值,且由Gap值的计算可知,虽然IGWO在剩余的3个算例中未取得最佳结果,但其Gap平均值为最小,说明整体仍有较好的表现。 分析其原因:1)本文随机游走策略是让一部分狼进行局部探索,这种方法有效提升了算法的广度搜索能力;2)尾部淘汰策略去除了表现较差的解,用新生成的解替代差的解,在补充解多样性的同时,有利于提升算法的收敛能力。 其次,为验证IGWO算法在求解FJSP时的性能,对于Brandimarte数据集,将IGWO算法与文献[25]的DPSO算法、文献[26]的MATSLO算法、以及文献[27]的heuristic算法进行对比;对于Kacem数据集,将IGWO算法与DPSO算法、文献[28]的ABC算法以及heuristic算法进行对比。各种算法在Brandimarte实例和Kacem实例上的对比结果分别如表7和表8所示,其中,粗体表示相同算例下各算法经过比较后的最佳结果。 表7 Brandimarte算例对比 表8 Kacem算例对比 由表7和表8中的数据可以看出,在Brandimarte测试用例的10个算例中,IGWO算法在其中5个算例上均能够获得当前最优解;在Kacem测试用例的5个算例中,IGWO算法在其中4个算例上均有最好的表现。整体来看,IGWO算法可获得60%以上的当前最优解。 同时,通过数据也可发现,IGWO算法并未在所有算例上都具有最好表现,尤其是在Brandimarte测试用例中有5个算例不是当前最优解。但结果展示,其他各个表现好的算法是分散在不同的算例上的,并未出现总体均优的算法。 为进一步说明IGWO算法的优化性能,本文计算了各种算法在Brandimarte实例上的Gap值及其平均值,计算方法参考公式(14),对比结果如表9所示。通过对实验结果分析发现,IGWO的Gap值为6.02%,接近表现最好的DPSO,这说明本文所提算法的寻优能力还是较好的。 表9 Brandimarte算例Gap值对比 IGWO与GWO相关算法和与其他群智能算法在Brandimarte算例上的Gap值比较如图8所示。 由表9和图8可知,IGWO算法对求解FJSP有较好的寻优能力。综合表6~表9中的数据以及图8可得,在求解以最小化最大完工时间为优化目标的FJSP问题时,本文提出的IGWO算法具有一定的有效性。 (a) GWO相关算法Gap值比较 本文针对柔性作业车间调度问题特点,基于经典灰狼算法提出了一种改进的灰狼优化算法,主要工作在于3个方面:1)采用基于权重的编码,实现了对连续优化算法的离散化;2)采用随机游走策略,增强了算法的局部搜索能力;3)通过尾部淘汰策略实现了种群更新。最后通过在标准算例上进行的仿真对比实验以及Gap值的比较,验证了改进策略的有效性,并进一步提高了灰狼算法在求解FJSP时的优化性能。鉴于本文所提算法的优化性能良好,接下来考虑将灰狼算法应用于更为复杂的车间调度问题中,同时考虑改进算法的计算性能。
2.4 种群更新
2.5 算法步骤

3 实验分析
3.1 实验设计
3.2 参数设置



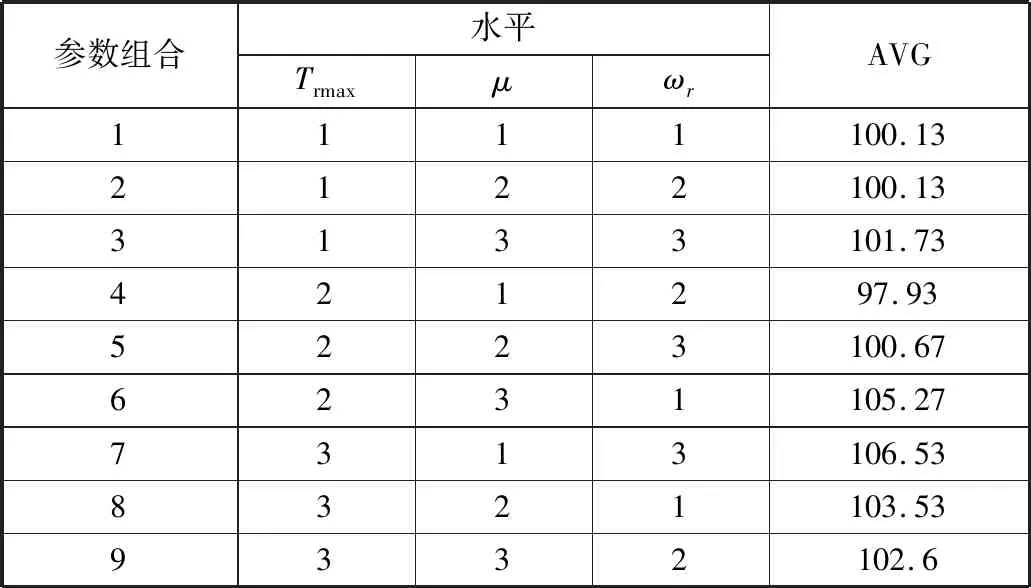


3.3 结果分析


4 结束语
