基于聚类分析的航班油耗组合估计

李 舒，张伟业，汪 坤，段照斌

(1.商飞软件有限公司,四川 成都 610000； 2.中国民航大学工程技术训练中心,天津 300300)

0 引 言

随着民用航空二氧化碳排放管理工作的推进，审查方开展碳排放核查迫在眉睫[1]。民用航空的碳排放主要来源于燃油消耗[2]，而航空公司提交的碳排放报告中燃油消耗数据常有缺失，数据的缺失会对核查结果产生重要影响，故研究缺失数据的估计具有重要意义。

对于缺失数据估计的研究已非常成熟，其中以朴素贝叶斯(NB)和动态时间规整(DTW)的研究最为深入。文献[3]使用NB方法对乘客缺少的属性进行估计；文献[4]在使用NB方法进行概率区间的预测；文献[5]使用改进的NB方法进行数据关联性估计填充；文献[6]使用NB方法对感知数据丢失进行了估计；文献[7]使用NB方法对船舶碰撞事故缺失数据进行插补；文献[8]使用NB方法对项目内缺陷预测的历史数据进行评估，但上述方法应用对象均属于不连续数据，不适用于连续数据和不连续数据的混合数据集，且少见于民航领域相关数据缺失的填充。文献[9]使用NB方法进行故障数据的填充；文献[10]基于NB的改进方法对数据缺失进行估计。文献[11]使用DTW方法评估复杂飞行动作以提高评估效率；文献[12]使用DTW分析了水文基于时间序列数据的相似性；文献[13]使用DTW方法对缺失的路段数据进行估计；文献[14]使用DTW扩增退化运动加速度参数；文献[15]基于DTW提出一种连续时间序列数据填充方法；文献[16]在工程预测领域使用DTW方法将不同运行条件或系统获得的数据扩充到当前系统中进行填充，上述方法应用对象均属于连续数据，亦少见于民航领域相关数据缺失的填充，而传统的飞机油耗估计[17-20]均使用深度学习算法进行数据的拟合与估计，与本课题中数据缺失估计应用方向不同。故本文提出一种民航领域的NB与DTW组合估计方法。文献[21]中对于偶然数据使用NB方法进行估计，对于多发性数据使用DTW进行估计，使用了NB与DTW组合估计方法，一方面不属于民航领域应用，另一方面虽减少了估计误差但数据分类效果欠佳，而K-medoids聚类分析具有良好的聚类效果[22]。

综上所述，本文在航空数据应用领域提出一种基于聚类分析的NB与DTW组合估计方法，首先将真实数据中的缺失采用K-mendoids聚类算法分类为单个不连续缺失和连续缺失2种类型；然后利用数据时空的相似性针对这2种类型的特点，分别采用NB和DTW的方法对航班缺失数据进行估计；最后利用均方根误差作为该方法的评价指标。

1 基于聚类分析的组合估计方法

1.1 聚类算法

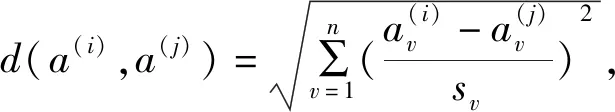
1)随机选取K个数据对象作为初始聚类中心。

2)计算剩余对象到各聚类中心的距离，并分配至距离最近的簇中。

3)选择簇内距离和最小的数据对象为作为新的中心点。

4)重复步骤2～3直至聚类误差和最小不再发生变化。

1.2 单个不连续缺失数据估计方法

采用NB方法计算单个不连续缺失数据时具有快速简单的优点，该方法利用历史同一时间点和上一时间点的油耗数据来估计当前缺失数据，将数据簇标记为K个油耗组，将油耗数据转化为K个油耗离散值。用同一航班同一日期历史油耗cH和同一航班上一日期油耗cS作为输入参数，估计航班当前日期的油耗c，估计公式[26]如下：

(1)

其中，P(c)为该航班某一日期的油耗估计值为c的概率；P(c|cH,cS)为该航班历史油耗为cH且上一日期油耗为cS的条件下该航班当前日期油耗为c的概率；P(cH,cS|c)为该航班油耗为c的条件下同一航班历史油耗为cH且上一日期油耗为cS的概率。由于cH和cS相互独立，式中∑P(cH,cS|c)P(c)对所有的c都相同，只需比较式(1)中分子的大小，因此估计公式可简化为：

(2)

其中，P(cH|c)为该航班油耗为c的条件下同一航班历史油耗为cH的概率；P(cS|c)该航班油耗为c的条件下同一航班上一日期油耗为cS的概率。具体计算公式[27]如下：

(3)

其中，N为3年内的所有油耗数据量；I(ci=c)为ci=c的布尔值，若ci=c则I(ci=c)=1，否则为0；I(cs,ci=c)为cS统计量的布尔值，若ci=c时存在cS则I(cs,ci=c)=1，否则为0。

(4)

其中，N为1年内的所有日期的油耗数据量；I(ci=c)为ci=c的布尔值，若ci=c则I(ci=c)=1，否则为0；I(cH,ci=c)为cH统计量的布尔值，若ci=c时存在cH则I(cH,ci=c)=1，否则为0。

(5)

其中，N为3年内的所有油耗数据量；I(ci=c)为ci=c的布尔值，若ci=c则I(ci=c)=1，否则为0，M为c取值的数量。

1.3 连续缺失数据估计方法

对于连续2个或以上的油耗数据点缺失，这种情况下NB方法已不适用[28]，考虑以最相似航班的油耗数据进行估计。动态时间规整是一种衡量长度不同的时间序列相似度的有效方法[29]，本文在连续缺失数据估计时采用DTW的相似度算法，求解累计距离最小航班对应的规整函数以寻找最相似的航班。含有缺失项的航班作为源航班，按时间先后顺序标记为序列M={m1,m2,…,mi}，其中i为该航班的油耗数据总量，依次选取其他所有航班数据，记为NFLT={n1,n2,…,nj,…,nn}，其中FLT表示航班号，n为其他航班的油耗数据总量。计算每个航班与源航班序列的累积距离，序列匹配距离计算如下：

(6)

其中，D[i,j]为序列与mi、nj匹配时的累计距离，d(mi-nj)是2个数据点间的欧氏距离。采用27o-45o-63o的局部路径约束，路径最佳会跳过距离过大的点以减少不必要的计算[30]。比较累计距离可得到与源航班最相似的航班，依据该航班对应的离散值转化为对应的分组，在同组内寻找距离最小的数据去估计缺失的航班油耗。

1.4 基于聚类分析的组合估计方法

本文方法处理流程如图1所示。首先对于缺失数据使用采用K-medoids聚类算法将数据集分为若干个簇，然后对单个不连续缺失数据使用NB算法进行估计，连续缺失数据使用DTW方法，使用分类组合的方式形成缺失数据组合估计方法，最后进行评估结果评价。

图1 基于聚类分析的组合估计方法

2 方法验证过程

选取近3年的B737飞机不同航段的航班部分燃油消耗数据，以实飞距离、轮档时间和业载作为影响航班油耗的飞行特征指标，提取实验样本总量为18316条。缺失航班油耗数据格式如表1所示，表中NULL代表数据缺失。

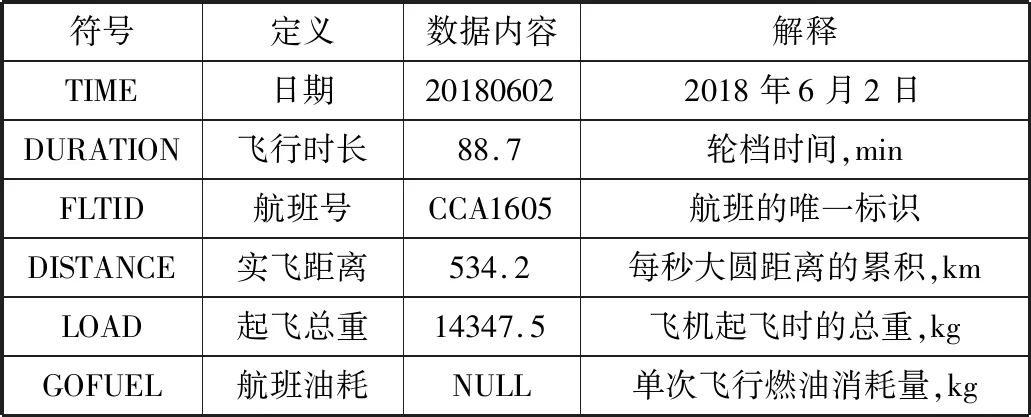
表1 缺失航班油耗数据格式

2.1 单个不连续缺失数据相似性验证

以航班油耗c所在分组为横坐标，输入参数cS或cH所在分组为纵坐标，灰度深浅代表条件概率的大小，两者的相关性如图2(a)所示。两者呈现较强的正相关性，可知相邻日期的航班相似的概率很大；图2(b)相比图2(a)概率分布较为分散，但仍集中在对角线附近，c和cH仍具有正相关性，概率分布不集中主要是因为历史数据样本数量有限，增加历史数据样本量，可发现概率分布更加集中，呈现更强的正相关性；由图2(c)可以看出cS和cH并无相关关系，两者相互独立。

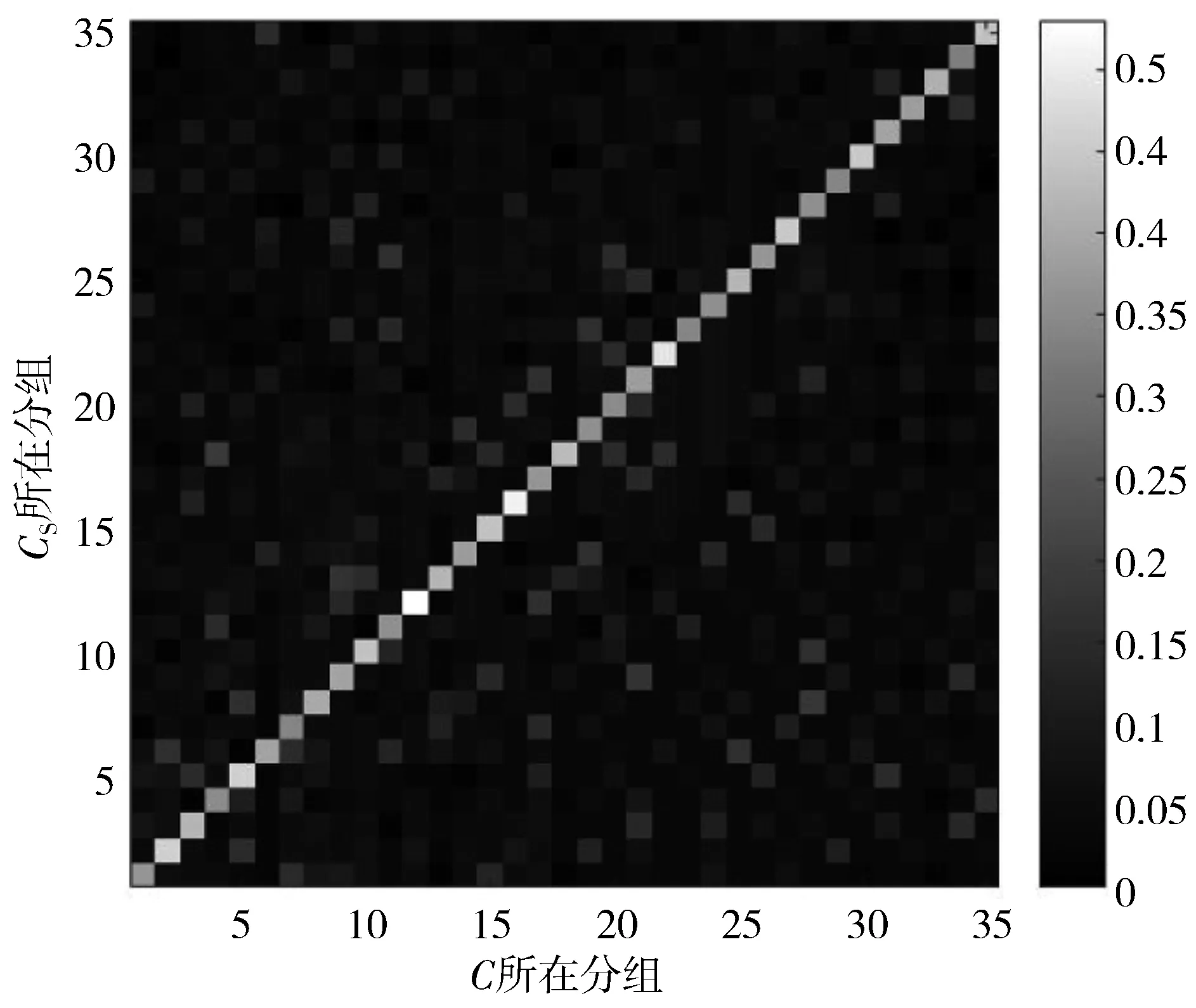
(a)

2.2 连续缺失数据相似性验证

将某航班一年内的油耗数据转换的k个离散值，按时间先后得到一组时间序列作为源航班与其他航班的时间序列比对，通过DTW的计算寻找到与源航班相似的航班，源航班和相似航班油耗序列对比，结果如图3所示。

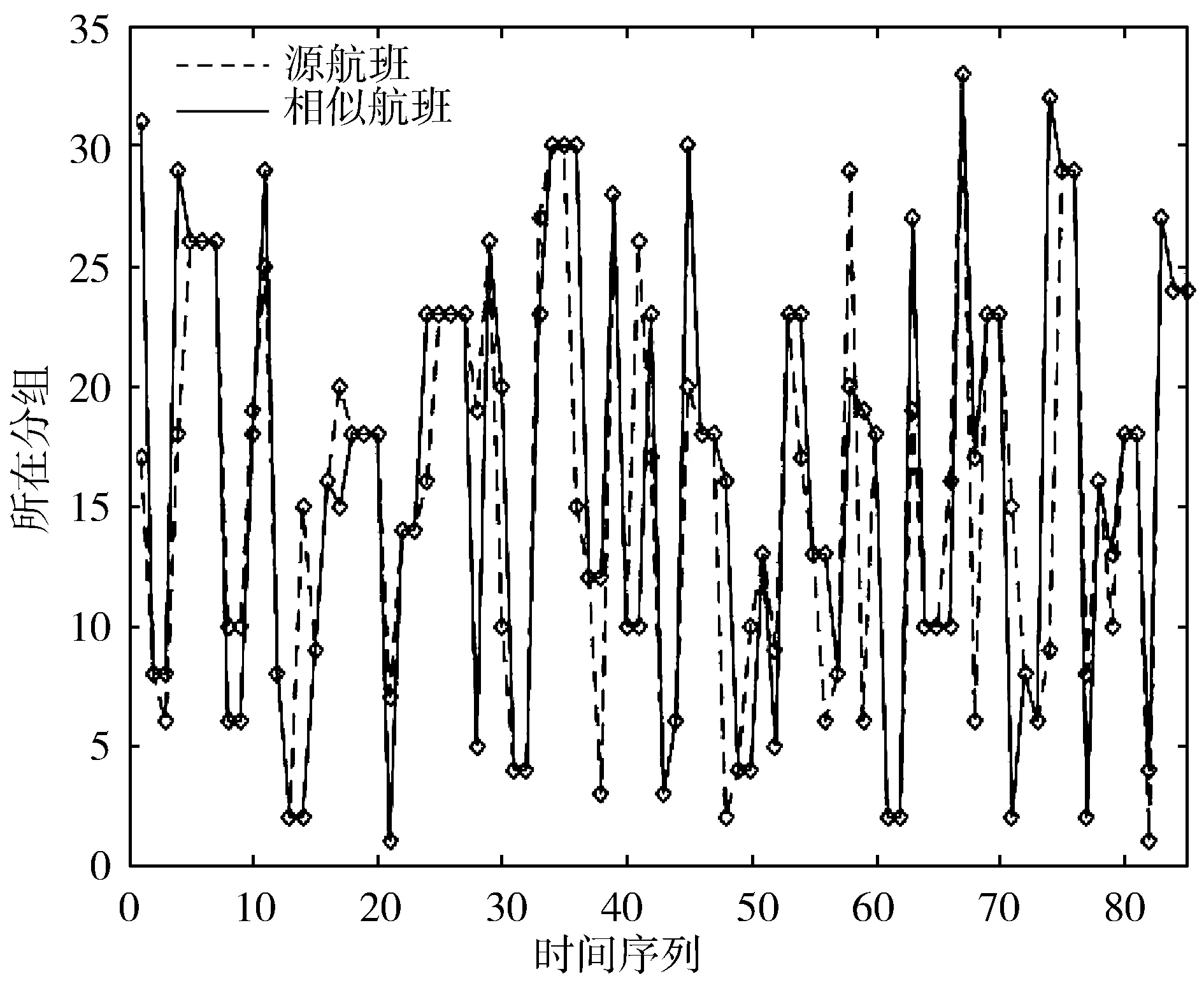
图3 源航班与相似航班的时间序列变化对比

在图3中截取本年度部分数据进行对比可知：相似航班时间序列的整体形状相近，由差值可知航班间的相似度很高，对应点重合的占比为59.3%，占比在52.7%至71.3%范围内，故此方法寻找出的相似航班具有一定的可靠性。

2.3 基于聚类分析的组合估计方法验证

审查方核查航班数据要求缺失率不应超过5%，定义缺失数据点占总样本点的百分比为缺失率。从样本数据中选取1%、2%、3%、4%、5%的样本点作为缺失数据，随机设置单个不连续和连续2种类型的缺失，人为构造不同数据集的缺失率，然后再通过均方根误差(RMSE)作为评价指标[31]比较不同方法的估计误差。

(7)

其中，n为缺失数据点总数；obsi为真实数据的观测值；prei为方法的估计值。

观察K的不同取值对于估计结果的影响，如图4所示随着K的增加，在K=35。附近时达到最小值，先减小后缓慢增加，因此本文设置K=35。在K值相同时，RMSE随数据缺失率的增加有一定程度增加，当缺失率为5%时，估算误差有明显增加，由于NB和DTW均以现有数据为输入参数，数据量的过度缺失将会明显提高方法的估计误差。

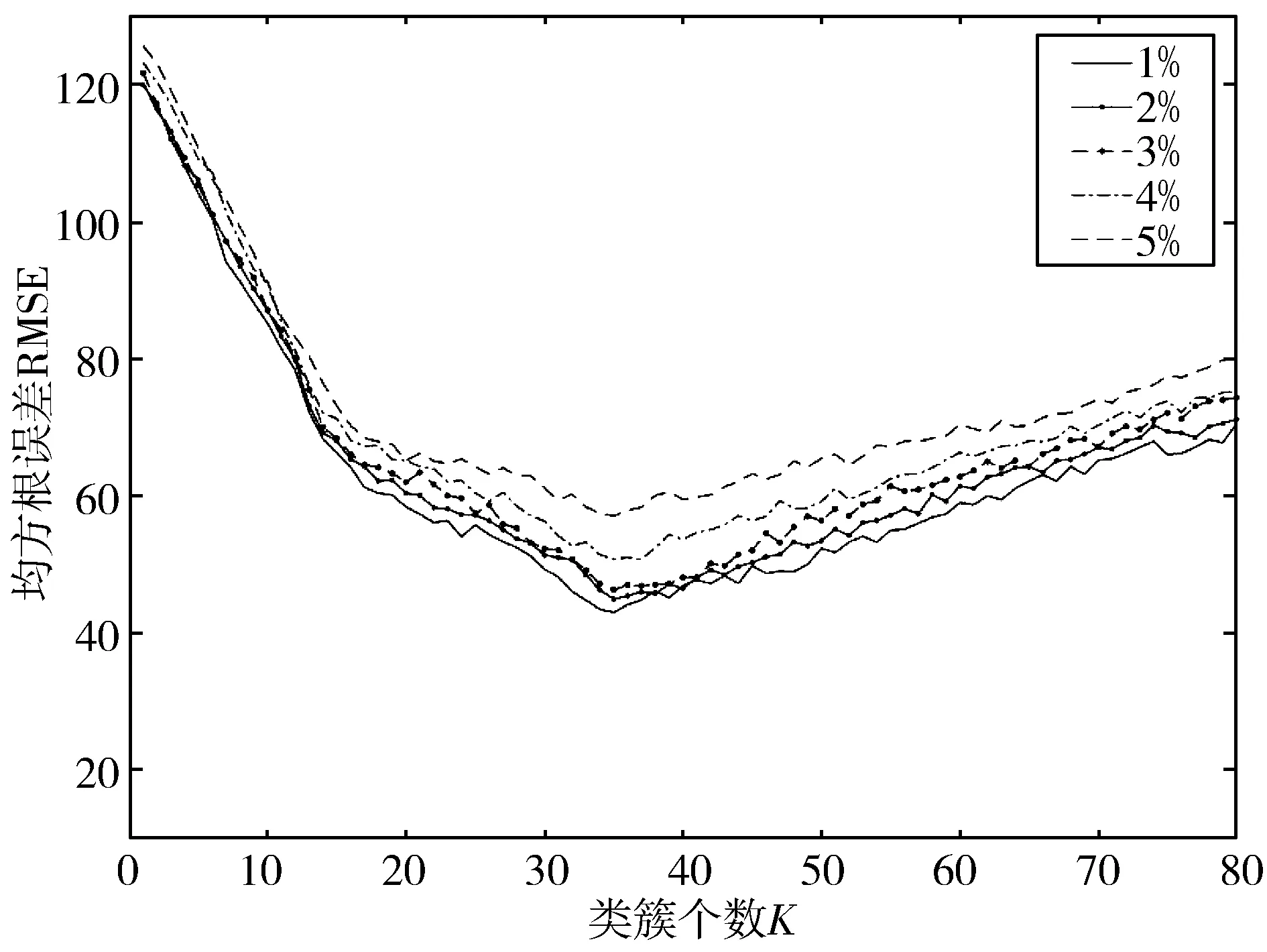
图4 NB-DTW方法估算误差与类簇个数K的关系

方法的估计误差比较结果如表2所示，可知，在相同缺失率下单独使用DTW均方根误差均大于两者组合使用，NB-DTW的估计误差较小。随着缺失率增大单独使用NB或DTW都会使方法的误差增大，NB采用缺失较多的数据作为输入参数，将会增大估计的误差；DTW采用欧氏距离寻找相似航班，缺失的数据可能会对计算过程产生影响，造成与非相似航班的混淆，使计算结果产生偏差。

表2 方法误差对比

分别单独使用2种方法对2类缺失数据进行估计，经验证NB对于连续缺失数据误差易累积，且估计结果不可靠，DTW相比于NB对于单个不连续的缺失数据的估计误差偏大。

3 结束语

本文以碳排放报告中燃油消耗数据为研究对象，提出一种基于K-medoids的NB-DTW组合估计方法。该方法有效地解决了使用单一方法估计多数据类型误差大的问题。在对碳排放报告中燃油消耗数据的缺失数据估计时，基于K-medoids的NB-DTW组合方法在1%、2%以及3%均方根误差时比NB方法分别降低了9.3%、12.1%、12.96%，比DTW方法分别降低了35.46%、43.62%、55.04%，能较好地估计碳排放报告中燃油消耗数据的缺失数据值，为民航数据估计提供一定的理论基础与工程思路。