采用显式动力学的轴承性能退化评估指标构建
2022-08-18张龙张号周建民彭小明王晓博乔宇
张龙,张号,周建民,彭小明,王晓博,乔宇
(华东交通大学载运工具与装备教育部重点实验室,330013,南昌)
滚动轴承作为现代机械关键零部件,决定着机械健康状态及剩余寿命,滚动轴承状态准确监测为设备健康运行及维护提供了保障[1-2]。时域振动信号作为采集的原始波形,所包含的信息含量最完整、最全面,其统计特征(峰值、均方根、峭度等)常用于揭示轴承性能退化过程[3-4]。实际工程应用中,轴承转速和载荷处于非平稳(小范围的波动)状态,选择对工况不敏感的统计特征才能更好地监测轴承状态。因此,选择最优特征及构建轴承性能退化评估指标一直以来都是研究的热点。
针对轴承信号最优特征的选择问题,Li等[5]结合支持向量机单特征评估,并通过相关性和主成分分析提出一种加权多维特征融合方法,试验证明了该方法比单域作为特征评估轴承性能退化趋势更有效。刘蕴哲等[6-7]针对时域、频域特征,通过距离评估准则和固有模态函数的排列熵及Hilbert谱的奇异值确定敏感性较强、分类效果较好的多域混合特征集。Tubishat等[8]基于变异算子的局部搜索算法和改进蝴蝶优化算法,提出了动态蝴蝶优化算法,该算法能够保留信息量最大的特征并且舍弃不相关特征。上述学者通过单域、多域特征融合和寻优算法确定优选特征,在特征选择的过程中未考虑轴承所受外部非平稳载荷和转速的影响,而在实际工程应用中,非平稳工况是不可避免的。
对于轴承性能退化评估指标构建的问题,张龙等[9]针对均方根对早期故障不敏感的问题,提出新型性能退化指标熵能比跟踪轴承性能退化发展趋势。黄海凤等[10]为解决早期性能退化识别困难的问题,采用盲源分离法分离噪声干扰后,将峭度值作为敏感特征用于轴承性能退化状态监测。Zhu等[11]为解决信号冲击成分微弱且环境噪声干扰严重的问题,提出一种基于改进模糊熵的轴承性能退化评估方法。上述学者针对性能退化监测做了进一步的研究,但对不平稳工况下早期微弱故障的识别未有涉及。实际工程应用中轴承工作状态具有非平稳特点[12],特别是轴承处于早期微弱故障阶段,特征信息微弱,且受到机械设备产生的强噪声干扰,给早期微弱故障的识别带来困难。
本文考虑实际工程应用中轴承转速和载荷的非平稳状态,通过显式动力学算法研究滚动轴承转速波动、径向载荷波动及转速和径向载荷同时波动工况下统计特征敏感性,以及外圈故障增长过程振动信号统计特征敏感性。选择对工况不敏感但对故障程度敏感的统计特征重构最佳特征,通过重构最佳特征的FSI监测轴承性能退化趋势。
1 时域统计特征
本文从时域统计指标出发,研究非平稳工况统计特征变化趋势。搜集了常见的17种时域振动信号的统计特征参数[13-14],分别是均值、均方根、方根幅值、绝对均值、偏度、峭度、方差、最大值、最小值、峰峰值、标准差、波形指标、峰值指标、脉冲指标、裕度指标、偏度指标、峭度指标,对应标签1~17。17个统计特征参数表达式如表1所示。

表1 振动信号时域特征参数
2 不同工况振动信号的仿真分析
2.1 轴承有限元模型建立与可靠性分析
2.1.1 建立轴承有限元模型
建立N205EM轴承二维显式动力学模型,将外圈故障简化为矩形凹坑,研究非平稳工况轴承统计特征的敏感性。滚动轴承几何参数是:节圆直径为38.75 mm,滚动体直径为6.75 mm,滚动体个数为12,接触角为0°,径向载荷为2 000 N,转速为2 100 r/min。
平面应变单元可以模拟轴承的运转状态,因此以二维应变壳单元代替轴承的实体结构[15]。轴承内、外圈和滚动体材料为GCr15,保持架材料为黄铜。
本文在满足实际情况的条件下对轴承座进行简化,外圈过盈安装在轴承座中,在内圈内表面施加径向载荷,方向为Y正向。在内圈内表面施加转速,方向为顺时针,采样频率为64 kHz。为更好地反映滚动体与内圈和外圈接触时的振动特性,将外圈内滚道、内圈外滚道网格细化。滚动轴承有限元模型如图1所示。

图1 轴承有限元模型
2.1.2 轴承有限元模型可靠性验证
滚动轴承显式动力学模型的可靠性保证了本文研究结果的可靠性,因此验证轴承有限元模型的有效性尤为必要。通过包络谱分析,得到的仿真信号时域和包络谱波形如图2所示。由于二维轴承模型为点对点接触,因此采集的振动信号幅值较大[16-17],将时域信号幅值与重力加速度比值作为纵坐标。从图2中可以看出,仿真信号包络谱中出现了故障特征频率的1倍频、2倍频、3倍频。

(a)仿真信号时域波形
外圈理论故障特征频率为
(1)
式中:D为滚动体直径;n为内圈转速;d为节圆直径;Z为滚动体个数;α为接触角。
由式(1)得到外圈理论故障特征频率为173.2 Hz,有限元仿真得到的外圈故障特征频率为172.6 Hz,两者相对误差为0.35%,由此证明本文模型的有效性,为后续分析工作的开展提供了可靠保障。
2.2 统计特征对工况和故障程度的敏感性分析
工程应用中,轴承载荷和转速在一定范围内波动。为分析时域特征对非平稳工况的敏感性,将轴承转速、径向载荷波动划分为恒载荷恒转速、变载荷恒转速、恒载荷变转速、变载荷变转速4种工况。
假设载荷、转速波动符合正弦曲线。参照图1,内圈内表面施加径向载荷:恒定载荷F=2 000 N,正弦径向载荷F=2 000+100sin(100t)。内圈内表面施加转速:恒定转速n=220 rad/s,正弦转速n=220+11sin(100t),t为时间。径向载荷、转速变化趋势如图3所示,可知径向载荷增加时,转速会降低,因此径向载荷与转速同时波动时两者趋势相反。
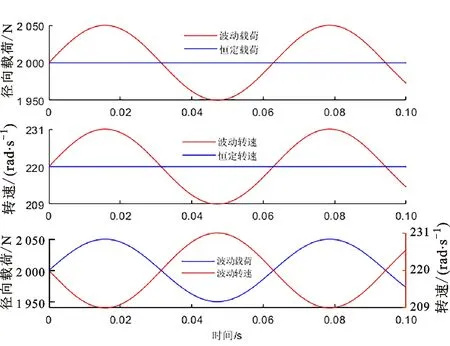
图3 非平稳工况曲线
2.2.1 正常轴承信号统计特征对工况敏感性分析
仿真正常轴承恒载恒速、变载恒速、恒载变速、变载变速4种工况,时间为0.1 s。提取轴承座一节点Y方向振动信号,4种工况下振动信号曲线如图4所示。
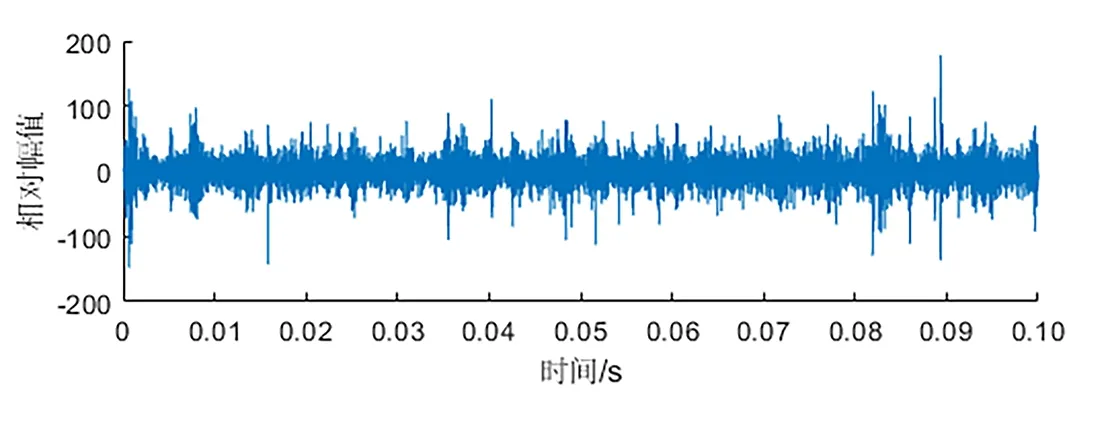
(a)恒载恒速
从图4可以看出,不同工况下振动信号曲线明显不同,故时域统计特征对工况的敏感性有所区别。比较不同工况下统计特征敏感性,其结果如图5所示,图5中纵坐标表示两种工况统计特征幅值占所有工况特征幅值绝对值之和的比例。

图5 不同工况时域信号的特征比
从图5中可以看出,均值受工况影响较大,单种工况波动下,均值出现较大差异,而在径向载荷及转速同时波动下,均值的绝对差值达到了100%,说明载荷和转速同时波动时,均值受影响更大。偏度和偏度指标对单种工况波动敏感性很强,在径向载荷或转速单独波动时,偏度和偏度指标的绝对差值均达到100%,说明此时出现分布不同的两种偏态,即正偏态、负偏态。而在两者同时波动工况下,偏度和偏度指标绝对差值降低,不对称程度降低,产生这种现象的原因可能是转速、载荷同时波动抵消了振动信号的不对称分布。相比平稳工况,有量纲指标均方根、方根幅值、绝对均值、峭度、方差、最小值、峰峰值和标准差在单种工况及复合工况波动下的绝对差值均处于10%以内,仅有最大值的绝对差值达到20%,上述统计特征对径向载荷和转速波动的敏感性较低。无量纲的峰值指标、脉冲指标和裕度指标对径向载荷波动的敏感性高于对转速以及转速和载荷同时波动的敏感性,且三者的敏感性相差不大,并未体现无量纲指标敏感性低于有量纲指标敏感性的优势。无量纲的波形指标、峭度指标对单种工况及复合工况波动的敏感性较低,体现了无量纲指标的优势。
将4种工况下的时域统计指标敏感性绝对差值累加,得到各时域指标对转速和载荷波动的综合敏感性,结果如图6所示。从图6可以看出,波形指标对转速和载荷波动的敏感性最低,峭度指标和裕度指标的敏感性相比于均方根、绝对均值的敏感性较大,偏度指标对转速和载荷波动的敏感性很高。
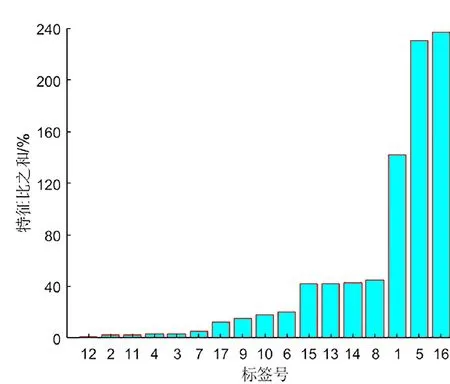
图6 不同工况时域信号的特征比之和
2.2.2 故障轴承信号统计特征对工况敏感性分析
轴承发生故障后,其动态特性变得更加复杂。在研究正常轴承信号的统计特征对转速和径向载荷波动敏感性的基础上,继续研究轴承外圈出现故障时域统计特征对转速、径向载荷波动的敏感性程度。
滚动轴承承载区在循环载荷作用下易发生故障,因此在轴承外圈Y正向位置处构建矩形故障,故障尺寸为0.25 mm×0.25 mm。径向载荷和转速波动工况下振动信号如图7所示。轴承外圈发生故障后,滚动体经过故障点产生冲击,且冲击幅值远大于经过正常位置时的幅值。
从图7可以看出,恒载恒速工况滚动体经过故障时冲击幅值较小,转速、载荷波动或转速和载荷同时波动时,滚动体经过故障点时幅值明显增加。提取信号时域的统计特征,比较故障轴承对工况的敏感性程度,结果如图8所示,其中纵坐标表示两种工况统计特征幅值占所有工况特征幅值绝对值之和的比例。

(a)恒载恒速
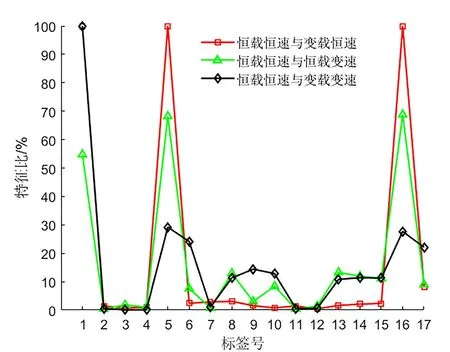
图8 不同工况时域信号的特征比
从图8可以看出,轴承外圈发生故障后,均值对转速和载荷波动的敏感性相比于正常轴承更高,均值对载荷波动的敏感性高于转速波动,且绝对差值达到了100%。偏度、偏度指标对转速和载荷的波动敏感性仍然较大,但载荷、转速同时波动降低了偏度和偏度指标敏感性,原因可能是载荷和转速波动的趋势相反,使振动信号不对称程度降低。轴承外圈发生故障后,均方根、方根幅值、绝对均值、方差和标准差对转速、载荷波动的敏感性很低,峭度、最大值、最小值和峰值对转速和载荷波动的敏感性有所增加。波形指标对转速和载荷波动的敏感性最低,峰值指标、脉冲指标、裕度指标和峭度指标相对于偏度指标敏感性不高,相对于波形指标敏感性较高;除去偏度和偏度指标,其他统计特征均对某一种工况敏感,例如最大值、脉冲指标和裕度指标对载荷波动较敏感,最小值、峭度和峭度指标对载荷及转速同时波动较敏感。
将4种工况下的时域统计指标敏感性绝对差值累加,得到转速和径向载荷波动工况下各时域统计指标综合敏感性程度,结果如图9所示。从图9可以看出,无量纲指标对转速及载荷的敏感性并不是最低。无量纲指标相比于部分有量纲指标敏感性较高,但其敏感性程度总体较低。

图9 不同工况时域信号的特征比之和
2.2.3 统计特征对故障增长敏感性分析
在恒载恒速下,随着外圈故障增长,各时域统计特征变化趋势如图10所示,纵坐标表示每一种故障尺寸下轴承信号统计特征幅值占所有故障尺寸类型统计特征幅值总和的比例。随着故障增加,统计特征值呈单调趋势,说明该特征表征故障增长的能力越好。从图10可以看出,均方根、方根幅值、绝对均值、方差、最小值、峰峰值、标准差和峭度指标能更好地表征故障的增长趋势。
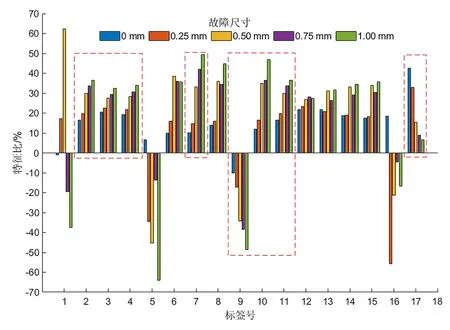
图10 不同故障程度下统计特征变化趋势
3 构建性能退化指标
轴承健康状况监测的主要任务是确定一个指标,该指标能表征轴承性能退化过程[18]。通过2.2节对时域特征的敏感性分析,得到绝对均值和均方根不仅对各类非平稳工况综合敏感性较低,且对故障增长敏感性较高。选择绝对均值和均方根重构最佳特征,基于重构最佳特征构建性能退化指标过程如下。
步骤1:为挖掘振动信号更多信息,对采集的每个样本进行重构。其中一个样本的重构矩阵为
(2)
式中:k为数据嵌入维数;x为信号幅值;jk=n,n表示样本数据量。
步骤2:提取对工况不敏感但对故障程度敏感的统计特征,特征矩阵为
(3)
式中m为样本数量。
步骤3:由选择的时域统计特征构建最佳特征
(4)
式中xRMS0为正常样本的均方根。
为说明构建的特征表征故障程度变化的能力,与构建前特征进行对比,结果如图11所示,可知轴承发生故障时重构特征值突变更显著,且很好地衡量了轴承的退化趋势。
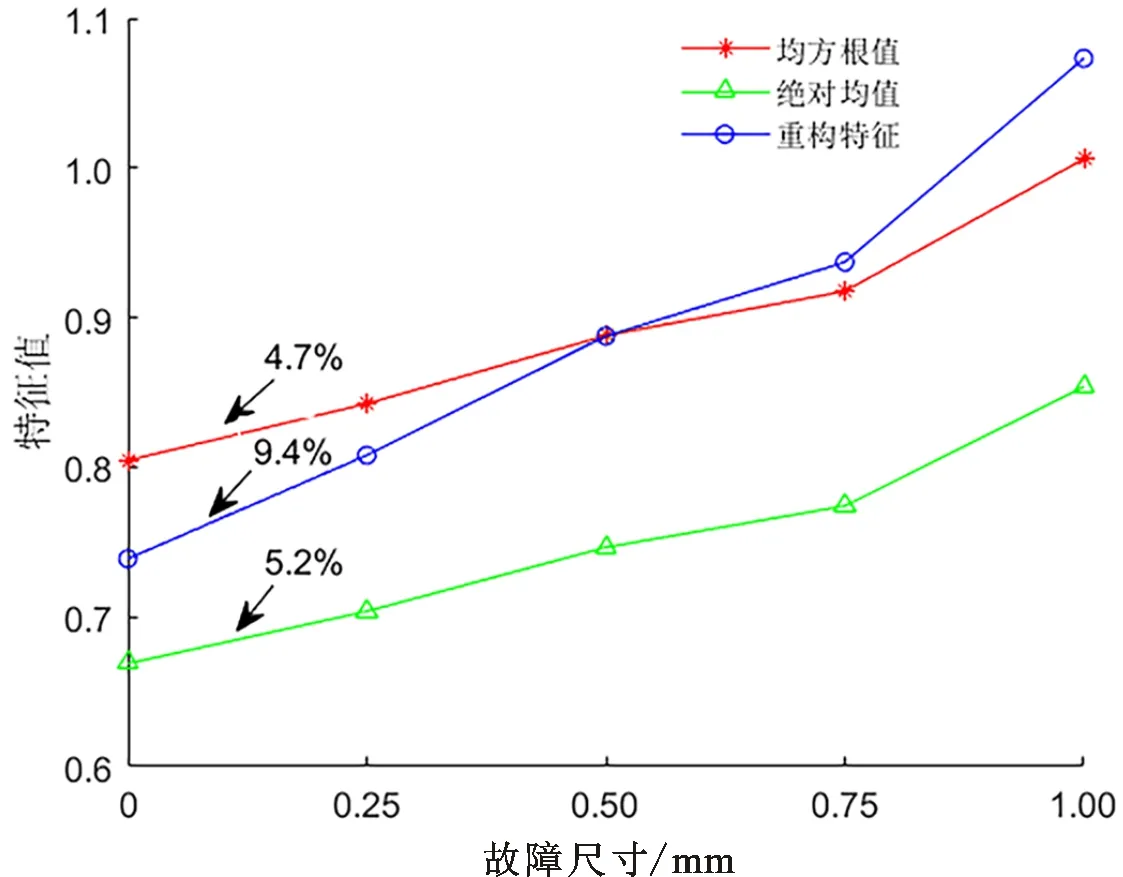
图11 特征重构前后表征故障能力
重构最佳特征矩阵为
(5)
步骤4:构建的性能退化指标FSI大小为
(6)
最终获得性能退化指标矩阵为
VFSI=[V1,2,V2,3,…,Vm-2,m-1,Vm-1,m]T
(7)
式中Vm-1,m为第m个样本与第m-1个样本的特征相似比。
4 试验分析
4.1 辛辛那提轴承疲劳试验数据分析
数据来自美国辛辛那提大学智能维护中心[19],滚动轴承运转采用带传动,带传动的过程转速处于非平稳状态。轴承型号RexnordZA-2115,节圆直径为71.5 mm,滚动体直径为8.4 mm,滚动体数为16,接触角为15.17°。电机转速为2 000 r/min,载荷为26 695 N,采样频率为20 kHz。选用轴承外圈故障数据集,样本数为984,每个样本数据量为20 480,轴承疲劳试验台如图12所示。

图12 轴承疲劳试验台
对于均值为μ、标准差为σ的正态分布或近似正态分布的随机变量来说,样本数值落在的概率为99.73%,当某个值超过该范围时,认为其不属于当前状态。计算数据集中200个正常样本的特征相似比,并以其μ+3σ值作为阈值[20]来判断轴承所处状态。
将最后两组异常数据剔除,分别计算剩下982组样本的RMS、FSI。RMS退化曲线如图13所示。以正常轴承FSI低于阈值及轴承发生故障后FSI突变量作为目标,确定最佳嵌入维数k为128,计算得到两样本之间FSI。经5点3次特征相似比性能平滑退化曲线如图14所示。

图13 均方根性能退化曲线
从图13中可以看出,在513时刻RMS超过阈值,之后RMS处于阈值以下,表明该时刻可能出现错误判断。轴承振动信号RMS在532时刻首次出现较大幅度增加,增加幅度为6.5%,且之后的RMS均超过阈值,表明该时刻健康状态可能发生改变。从图14中可以看出,轴承振动信号FSI在532时刻发生突变,突变幅度达到了21.8%,且532时刻之后的FSI均高于阈值。表明FSI有效识别了该时刻轴承健康状态的变化,并且未出现识别错误的情况。533~703时刻,FSI处于增长状态,说明轴承故障程度处于增长阶段,轴承劣化程度不断加深。703~853时刻,FSI先增加后降低,可以认为滚动体与外圈在摩擦力作用下,轴承在此阶段故障逐渐磨平,继续运行使轴承再次出现恶化。在853时刻之后阶段,轴承恶化程度不断加深。

图14 特征相似比性能退化曲线
比较图13、图14,由于轴承健康状态振动信号的随机波动,FSI在健康阶段波动较大。但FSI有效识别了早期微弱故障时刻,且未出现错误识别的现象,说明FSI作为评估指标具有准确性与有效性。从图14可以看出,FSI能很好地表征轴承性能的退化过程。
文献[21]分别对532、533、534时刻进行了包络谱分析,结果显示,轴承在532时刻未发生故障,在533时刻发生早期故障。这和本文的研究结果一致,进一步验证了所提方法的准确性和有效性。
4.2 XJTU-SY轴承疲劳试验数据分析
数据来自XJTU-SY[22],交流电机提供动力带动轴承转动,运转过程转速处于非平稳状态。轴承型号LDK UER204,节圆直径为71.5 mm,滚动体直径为7.92 mm,滚动体数量为8,接触角为0°。电机转速为2 400 r/min,载荷为10 kN,采样频率为25.6 kHz。选用轴承外圈故障数据集,故障频率为123.4 Hz,样本量为2 538,每个样本数据量取10 240。轴承疲劳试验台如图15所示。

图15 轴承疲劳试验台
计算数据集RMS和FSI,RMS退化曲线如图16所示。以正常轴承FSI低于阈值及轴承发生故障后FSI突变量作为目标,确定最佳嵌入维数k为72,计算两样本之间FSI。经5点3次平滑退化曲线如图17所示。

图16 均方根性能退化曲线
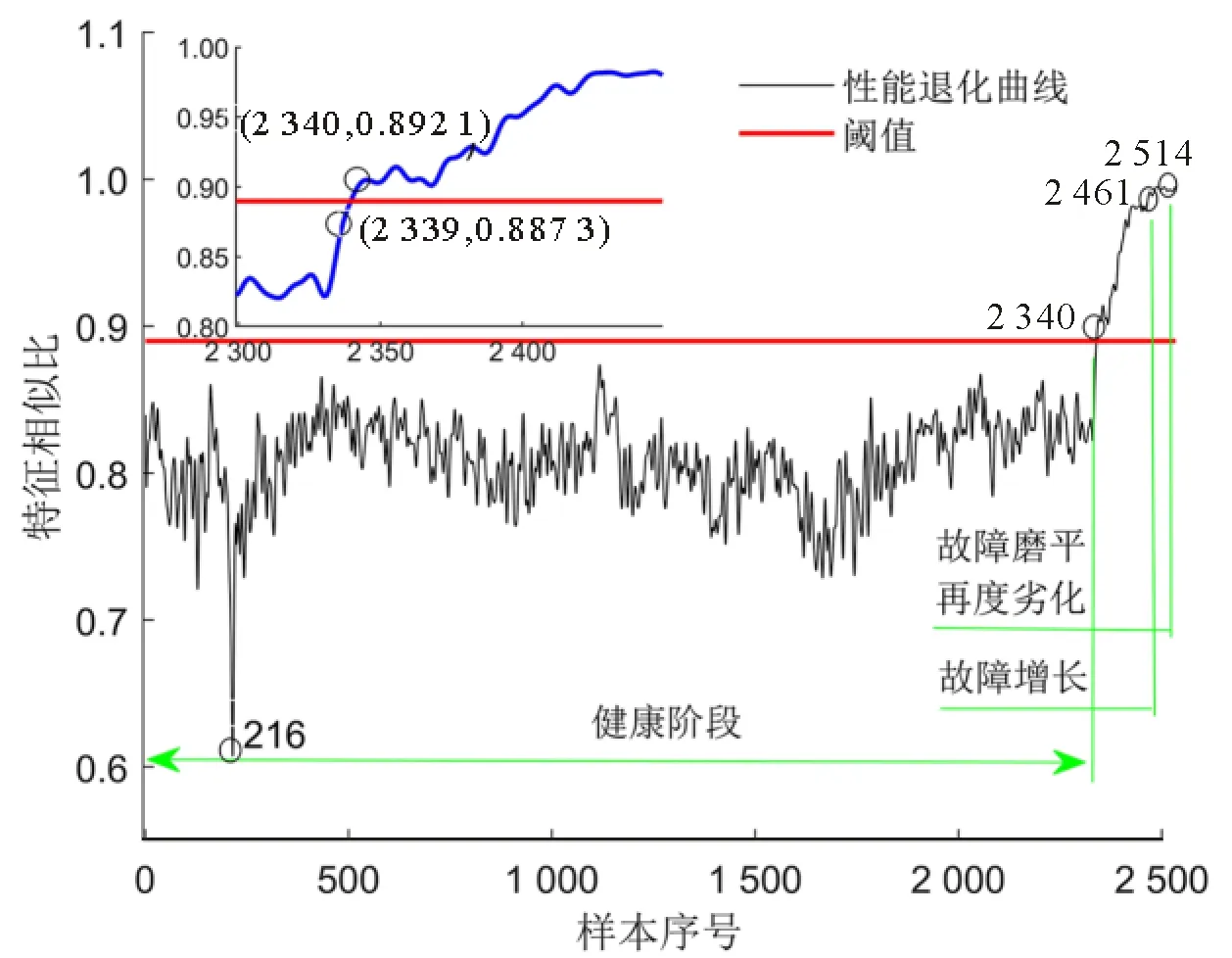
图17 特征相似比性能退化曲线
从图16可以看出,在2 336时刻RMS超过阈值,之后RMS处于阈值以下,表明该时刻可能出现错误判断。轴承振动信号RMS在2 340时刻之后均超过阈值,表明该时刻健康状态可能发生改变。从图17可以看出,轴承振动信号FSI值在2 340时刻及该时刻之后均高于阈值,FSI准确识别了该时刻轴承健康状态的变化,并且未出现识别错误的情况。2 340~2 461时刻,FSI处于增长状态,说明轴承故障程度处于增长阶段,轴承劣化程度不断加深。2 461~2 514时刻,FSI缓慢增加,可以认为滚动体与外圈在摩擦力作用下,轴承在此阶段故障逐渐磨平,继续运行使轴承再次出现恶化。在2 514时刻之后阶段,轴承基本失效。
与RMS相比,由于轴承健康状态振动信号的随机波动,FSI在一定范围内波动,在216时刻波动较大的原因可能是轴承部件之间的碰撞。FSI准确识别了早期微弱故障时刻,且未出现错误识别现象,该试验再次证明FSI指标的优越性。
为验证试验分析结果的正确性,对2 339、2 340、2 400时刻样本进行自适应频带滤波,得到滤波信号进行包络谱分析,其结果如图18所示。从图18可以看到,2 340时刻出现明显的谱峰,与2 400时刻倍频一致,且与外圈故障频率相近。2 339时刻几乎没有出现明显的谱峰,其值124.2 Hz较小,可认为是由噪声成分引起的,因此认为2 340时刻出现早期微弱故障。
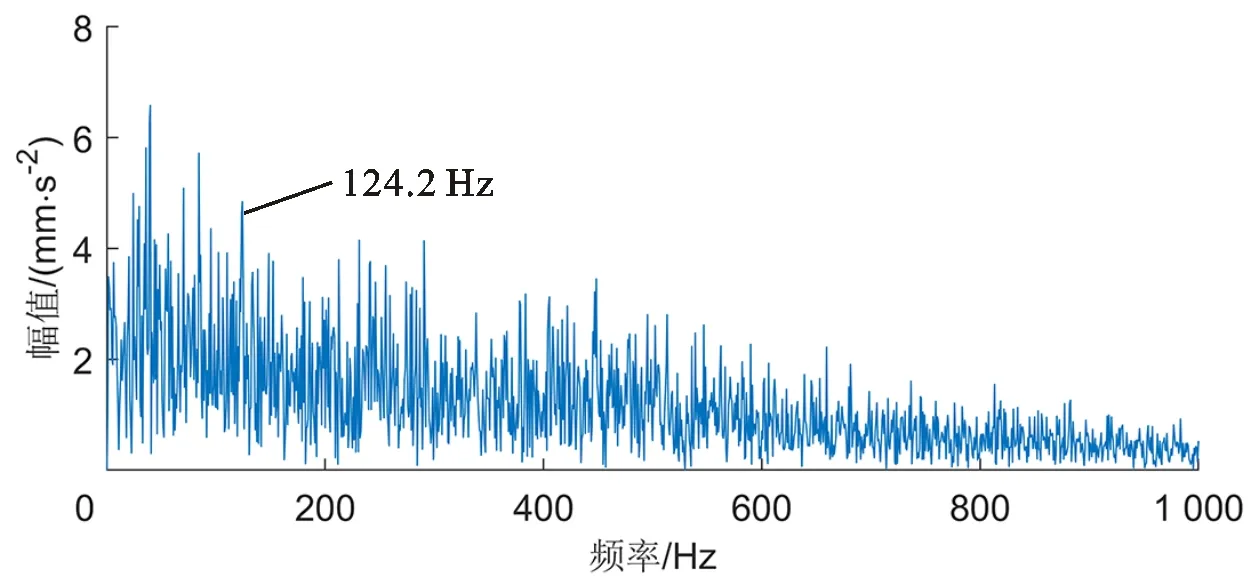
(a)2 339时刻包络谱
为验证本文所提指标的优越性,与3篇文献中得到的性能退化转折点进行对比,对比结果如表2所示。通过对比可得,本文所用方法能准确监测轴承性能退化转折点,且可以有效表征轴承性能的退化趋势。
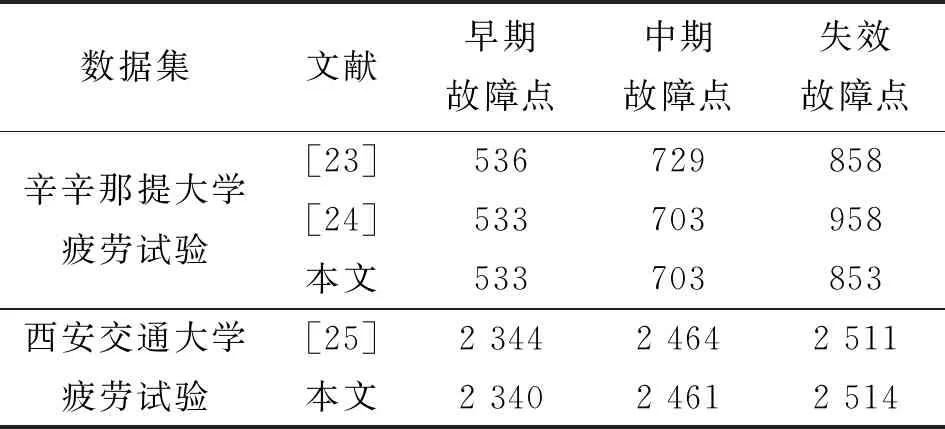
表2 性能退化转折点对比
5 总 结
针对实际工程应用中工况非平稳的情况,本文提出了一种新型性能退化指标,即特征相似比(FSI)。
(1)通过有限元法仿真了恒载恒速、变载恒速、恒载变速和变载变速工况下正常、故障轴承振动信号,分析了时域统计特征对非平稳转速、载荷和故障程度的敏感性。
(2)选择对非平稳转速和载荷不敏感但对故障程度敏感的特征集构建最佳特征,最终得到FSI。相比于均方根,FSI对故障程度变化更加敏感。
(3)通过分析非平稳工况下轴承全寿命疲劳试验数据,验证了FSI在非平稳工况下能准确识别早期故障时刻,与轴承性能退化趋势的一致性更好。
