强化学习性能最优控制框架及其在高压给水加热器运行优化中的应用

周东阳,曹军,毕胜山,邵壮,司风琪

(1.西安交通大学热流科学与工程教育部重点实验室,710049,西安;2.西安热工研究院有限公司,710054,西安;3.东南大学能源热转换及其过程测控教育部重点实验室,210096,南京)

电力行业在持续发展过程中对火电机组的生产技术提出更高的要求,除了最基本的运行稳定之外,还要求过程的高效与智能[1]。传统控制理论中较为成熟的控制器算法,通常将大多数控制任务都简化为设定点跟踪问题,从而通过将输出调节到设定值来确保闭环过程的稳定性。在大多数情况下,这些设定值是根据经验手动设置的,但是现代复杂的火电机组发电过程还需要对设备的性能指标进行优化,使其在运行工况不断变化的过程中保持最优,此时单一不变的设定值往往难以满足需求。现代控制理论在自动控制技术的发展中起着积极的作用,并衍生了最优控制[2]、自适应控制[3]、鲁棒控制[4]和模型预测控制(MPC)[5]等先进控制算法,可以在控制过程中同时实现系统性能优化,但是它们通常依赖对象的动态特性模型,因此对于某些动态特性难以辨识或存在时变的对象[6],这些基于模型的方法往往难以达到预期的效果。

凝结式给水加热器水位控制是火电机组的一项经典控制任务,目前使用最广泛的是比例-积分-微分(PID)控制器。控制器根据实时水位与目标水位的偏差,通过调节疏水阀,保持水位在目标水位附近。然而,机组负荷在运行过程中持续变化,会改变加热器的边界参数和系统的动态特性。作为设定点跟踪问题,控制器的目标是在不断变化的边界参数下保持水位稳定,但是无法考虑诸如加热器端差和给水温升之类的性能指标。为此,学者们围绕水位与加热器性能的关系开展了研究。Hossienalipour等[7]建立了一个数学模型来评估加热器的性能,定量分析表明,在某些工况下水位对加热器的换热性能影响很大,给定的水位设定值在大多数情况下都会使加热器偏离其最佳运行状态。Xu等[8]通过建立一个变工况特性模型,针对性能指标分析了变工况下的最佳水位设定曲线。但是,建立一个精确的数学模型来描述高压蒸汽在复杂物理结构中的凝结过程是非常困难的,其中有大量的换热特性参数需要通过实验手段获取。此外,文献[9]中还分析了的热交换器表面存在的劣化现象,这进一步阻碍了基于模型的优化控制方法的应用。

近些年,学者们提出了许多方法来满足运行优化控制的需求[10],包括基于模型的方法(如MPC[5]和实时优化(RTO)[11])和无模型的方法(如数据驱动的优化(DDO)[12-13]和强化学习[12,14-15])。基于强化学习的无模型最优控制方法可以直接利用观测数据求解控制器,而无需建立描述系统的解析表达式。由于计算能力的飞速发展,强化学习近年来受到了极大的关注,并显示出其在许多领域中解决广义控制问题的能力,如国际象棋[16]、跳棋[17]、网络资源分配[18]、视频游戏[19]、围棋[20]等。强化学习结合了动态规划和机器学习两种理论,用于求解序列决策问题的最优策略,在面对维度诅咒和模型不确定性的问题时具有一定优势[21]。通过观察控制器与对象交互的状态转移和相应的奖励信号,强化学习在累积奖励最大化的方向上更新状态、状态-动作组合的价值估计或直接更新控制器参数[22-23],以逐步改进控制器作用于对象的控制品质。目前,强化学习已在诸如电力系统控制[24]、飞行控制[25]、动态功率管理[26]、无人机[27]和机器人控制[28]等领域实现了应用。在过程控制领域,Jiang等[29]以浮选工艺为例,设计了基于强化学习的最优控制方法,使用过程生产效率的性能指标取代原有的设定点跟踪目标,证明了强化学习有助于提高过程控制品质和生产效益。

本文以高压给水加热器的水位控制为研究对象,首先介绍高压给水加热器的物理系统,并对最优控制的数学问题进行形式化,然后介绍基于强化学习的性能最优控制框架,最后利用某600 MW机组高压加热器的仿真模型对本文提出的方法进行验证。

1 高压给水加热器水位性能最优控制

目前,火电机组给水加热器主要使用PID控制器将水位控制在一个固定设定值附近[1]。然而,持续波动的机组负荷导致加热器的运行工况也在不断变化,而不同工况下最佳水位设定值却是不同的[8]。因此,如果水位设定值固定,则会使加热器偏离其最佳运行状态[7]。考虑到加热器凝结过程较为复杂,难以利用模型来确定不同工况的最佳水位设定值,本文采用基于强化学习的性能最优控制框架来解决高加水位控制问题。

图1给出了加热器的物理结构,其中给水从右下侧流入底部水室,平行地流经U型管,同时从管壁吸收热量,最终进入顶部水室并流向下一级的加热器。蒸汽侧分为蒸汽冷却段、凝结段和疏水冷却段共3个区域。过热蒸汽首先进入蒸汽冷却段,与管壁进行交叉对流换热,冷却至饱和状态后进入冷凝区,在U型管表面冷凝成水滴,并流入加热器底部形成疏水,随后通过水封进入疏水冷却区,与管壁进行交叉对流换热。过冷的疏水最终从加热器排出,通过控制阀,流入下一级加热器,控制阀通过调节疏水流量,使加热器水位达到给定的目标值水位。

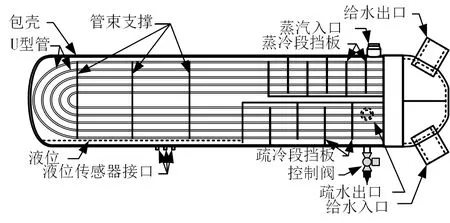
图1 典型高压加热器的物理结构

疏水水位随液滴凝结量的增加而升高,随疏水流量的增加而降低,其中液滴凝结量主要取决于冷凝区的换热量,它同时与管侧的给水流量、温度以及壳侧的蒸汽压力、温度等有关,疏水流量则取决于疏水调节阀的开度、当前水位及加热器压力。可见,给水的流量和温度、蒸汽的压力和温度是加热器的4个边界条件,影响加热器的动态平衡。水位的动态变化与上述边界条件之间的关系可描述为

(1)

式中:A(l)为水位为l时的横截面积;Qs为凝结液滴的总质量流量;Ps为蒸汽入口压力;Ts为蒸汽入口温度;Qw为给水入口质量流量;Tw为给水入口温度;Qd为疏水质量流量;Ps为当前抽汽级压力;l为水位;V为疏水阀开度;G(V,a)为执行器的动态特性;a为阀门开度变化率的控制信号。

为了保持加热器的热交换过程稳定且高效,在运行过程中应始终保持合适的水位。当水位太高时,疏水会浸没U型管,从而减少凝结段的传热面积;当水位太低时,疏水管中会混有蒸汽,降低蒸汽的利用率,还影响下一级加热器的换热过程。加热器的运行性能指标包括给水温升ΔTw、给水端差ΔTttd和疏水端差ΔTdtd。ΔTw是给水出口温度与给水入口温度之差,ΔTw越高则热力系统效率越高;ΔTttd是蒸汽入口压力对应的饱和温度与给水出口温度之差,ΔTttd越小则说明凝结段的传热性能越好;ΔTdtd是疏水温度和给水入口温度之差,ΔTdtd越小则说明疏水冷却段的传热性能越好。因此,给定蒸汽和给水的入口参数,好的加热器的运行状态所对应的ΔTw大、ΔTttd小、ΔTdtd小。边界条件和水位都会对ΔTw、ΔTttd和ΔTdtd造成影响[30],因此水位控制需要考虑在满足安全性与稳定性的同时优化上述性能指标。

2 性能最优控制问题的数学形式

将式(1)连续时间状态空间方程转化为离散形式

(2)

式中:F(·)为水位动态特性的差分方程;G(·)为执行器动态特性的差分方程。

高压给水加热器的离散时间性能最优控制问题的优化目标为

(3)

式中:γ∈(0,1]为折扣因子;[ω1,ω2,ω3,ω4]T∈4为3个性能指标和水位变化率的平方的权重向量;Pl,t为水位超限惩罚函数;Pa,t为避免疏水阀全开或全关的软约束函数;λl和λa分别为惩罚的权重;π(·)为控制策略函数;在限值之外的二次项形式是为了保证优化目标的一阶导数连续;Pl,t和Pa,t均为不等式约束,利用拉格朗日乘子将其引入到目标函数中,公式为

(4)

其中,lmax和lmin分别为水位上下限,Vmax和Vmin分别为阀位的上下限。

3 基于强化学习的性能最优控制框架

为了使用异策略连续动作强化学习算法解决式(3)所示的优化问题,同时避免性能较差的初始策略函数参与真实物理系统的运行。本文首先提出了基于强化学习的性能最优控制框架,然后重点介绍其中数据缓冲区的数据处理算法和用于求解策略函数的强化学习算法,最后利用两个算例对框架的性能进行验证。

图2给出了基于强化学习的性能最优控制框架。由图可知,基于强化学习的性能最优控制框架包括在线控制、数据预处理和策略函数求解共3个主要环节。首先通过在线控制环节生成大量历史运行数据,然后在数据预处理环节,利用均匀化网格算法(homogenization grid algorithm,HGA)算法对训练样本进行整理,最后在策略函数求解环节,利用基于粒子群优化的连续批量Q学习算法(particle swarm optimization continues batchQ-learning algorithm,PSO-CBQ)算法训练控制策略函数。最终得到的控制策略函数在通过性能测试之后,可以替代现有控制器,以改善系统的运行水平。

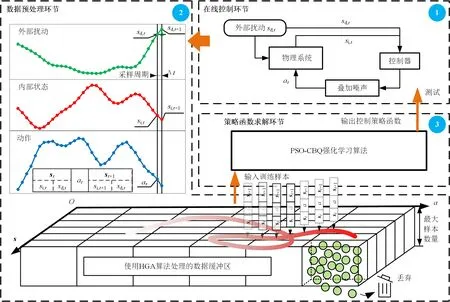
图2 基于强化学习的性能最优控制框架

3.1 在线控制环节

图2中的在线控制环节描述了真实物理系统受外部扰动和控制动作的共同影响而持续地进行状态转移的过程。真实物理系统在时刻t的内部状态为si,t,它在外部扰动sd,t和控制动作at的影响下,于t+1时刻转变为si,t+1,由t到t+1的状态变化称为一组状态转移样本。

为了提高状态转移样本的多样性,本文在现有控制器的输出上叠加了少量随机噪声,最终作用在真实物理系统的控制动作at满足以现有控制器实际输出为均值的正态分布

at～N(aonline,t,σ)

(5)

式中:aonline,t为现有控制器的输出;σ为扰动的方差。

3.2 数据预处理环节

图2中的数据预处理环节从时间序列中采集状态转移样本并生成用于训练策略函数的数据集。在样本采集过程中,需要将时间序列数据构造成st,at,st+1元组的形式,其中st=[si,t,sd,t]T而st+1=[si,t+1,sd,t]T。这里需要注意的是,st+1所包含的外部扰动是sd,t而不是sd,t+1,这是因为t+1时刻的外部扰动sd,t+1与t时刻的外部扰动sd,t无关且不由at决定,这样的设置隐含着外部扰动不会变化的假设,从而使策略函数倾向于将系统调节至稳定状态。

考虑到训练数据集中样本分布不均匀容易导致策略函数训练发散,本文提出了均匀化网格算法,其伪代码如下。

算法均匀化网格算法

1 初始化:结构为ds×da×Nmax的数组B,其中Nmax是单个网格中的最大样本数量,下边界向量Bl=[smin,amin]T,上边界向量Bu=[smax,amax]T,网格数量向量nc=[nc,s,nc,a]T

2 重复:

3 对于每一个从时间序列数据库采集的新元组st,at,st+1:

4 定义工况向量vc=[st,at]T

5 如果vc∈[Bl,Bu]:

6 计算网格索引向量vi=floor(((vc-

Bl)./[(Bu-Bl)./nc])),floor(·)为逐元素向下取整

7 将st,at,st+1插入网格B[vi]尾部

8 如果网格B[vi]长度大于Nmax:

9 将网格B[vi]的头部元素删除

HGA首先在st-at空间划分网格,建立数组结构的数据缓冲区B,处理时间序列数据时把st,at,st+1元组依次插入网格中,通过平衡各网格的元组数量,保证历史数据集在st-at空间分布均匀。HGA中的数据缓冲区B具有3个特性:①B中数据总量有限,可以避免冗余数据无限积累;②B中所有网格的数据量均处于同一数量级;③存储在每个网格中的数据会不断更新,更新速度取决于时间序列中该状态动作对出现的频率。相较于其他均匀化算法,HGA算法尽管不适合处理状态空间维度过高的问题,但是其计算量更小,因此在面对采样周期较短的连续动态优化问题时,可以有效地降低计算负载。

3.3 策略函数求解环节

图2中的策略函数求解环节利用从数据缓冲区采集的样本,使用异策略连续动作强化学习算法离线地求解控制策略函数。需要注意的是,当状态st为连续变量时,要使用参数化Q值函数Q(s,a|ωQ)∈来近似Q值函数,其中ωQ为Q值函数的参数。当状态st和动作at同时为连续变量时,还要使用参数化策略函数π(s|θ),其中θ为策略函数的参数,此时关于Q(s,a|ωQ)的最大化运算maxa、arg maxa求解效率较低,因此有必要对算法进行改进。

考虑到火电厂连续动态优化问题通常具有动作空间维度低的特点,本文使用粒子群优化[31-32]算法来求解最大化运算,即对于给定状态st和Q值函数,以Q(st,·|ωQ)为粒子群优化的适应度函数,通过在动作空间随机搜索,找到使适应度最大的动作,即为arg maxa的解,对应的适应度为maxa的解。

结合粒子群优化算法和Q学习算法,本文提出了基于粒子群优化的连续批量Q学习算法算法,其伪代码如下。

算法基于粒子群优化的连续批量Q学习算法

1 已知:数据缓冲区B

2 初始化:Q值函数Q(s,a|ωQ),∀(s,a),Q(s,a|ωQ)=0,目标Q值函数Qd(s,a|ωQd),其中,ωQd为目标Q值函数的参数,ωQd←ωQ,随机参数初始化的策略函数π(s|θ),给定Q值函数学习率α、策略函数学习率αθ

3 重复直到ωQ稳定:

4 从B中采集N个状态转移样本

5 对于第j个样本st,j,at,j,st+1,j:

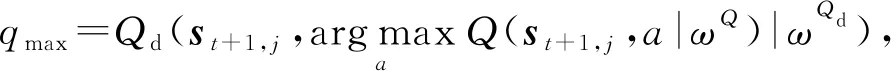
7rj=R(st,j,at,j,st+1,j)

8qj=Q(st,j,at,j|ωQ)+α[rj+γqmax-

Q(st,j,at,j|ωQ)]

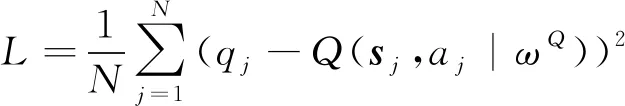
10 更新ωQd←(ωQ+ωQd)/2

11重复直到θ稳定:

12 从状态空间均匀采集M个样本,利用Q值函数和采样策略梯度对θ进行一步更新:

首先从数据缓冲区B中收集单步状态转移样本,然后根据初始Q值函数Q(s,a|ωQ),结合粒子群优化算法计算样本集中所有状态-动作对的损失函数,并使用梯度下降更新Q值函数的参数ωQ[33],随后重复该过程直到ωQ收敛,最后计算策略函数π(s|θ)的策略梯度θJ,并使用梯度上升更新策略函数的参数θ直至收敛。

4 算例分析

本文在Python-3.7环境下,在TensorFlow-2.0.0深度学习库的基础上实现了强化学习性能最优控制框架,并基于仿真运行数据来求解式(3)所示优化问题,以获得水位控制策略函数。首先,使用APROS-6.04仿真软件[34],以某600 MW机组#1高压加热器为研究对象建立了仿真模型,将其作为真实物理系统生成运行数据。该高压加热器模型的结构与参数如图3所示,该模型稳定状态在机组THA工况附近。

图3 APROS高压加热器仿真模型

采用基于强化学习的性能最优控制框架求解策略函数的超参数如表1所示,其中加热器运行工况范围等效于在500～600 MW之间。

表1 高压加热器水位性能最优控制算例的超参数

实验发现,策略函数采用浅层网络效果不佳,Q值网络采用深层网络的效果不佳。可能的原因在于式(3)所示的优化目标较为复杂,策略函数需要具备足够的特征变换能力,才能具备较好的控制效果,但又为了避免训练过程不稳定,因此适合选择多层少节点的网络结构。Q值网络需要具备较强的泛化能力,以防止对价值估计的过拟合,综合考虑适合选择少层而多节点的网络结构。奖励函数中的性能指标ΔTw,t、ΔTttd,t、ΔTdtd,t为

(6)

式中Tsat(·)为饱和蒸汽温度关于蒸汽压力的函数,根据IAPWS-IF97标准公式计算。

图4给出了Q值神经网络及其策略神经网络参数的平均绝对变化率的变化趋势。图中,蓝色阴影为10轮不同训练过程中95%置信水平对应的置信区间。可以看出,学习过程是不稳定的,网络参数的平均绝对变化率没有单调下降,且在300次迭代之前均存在较大的方差,不过在300次迭代之后逐渐稳定收敛。由此可知,使用神经网络逼近器的性能最优控制框架可以使学习过程收敛至局部最优解。

(a)Q值神经网络

为了验证基于强化学习的性能最优控制框架得到的策略函数的性能,使用某一个收敛的策略神经网络在设计工况附近进行阶跃实验,表2给出了设计工况稳定状态下系统的过程参数。

表2 设计工况稳定状态下的过程参数

在稳定状态下,将加热器水位设置为1,观察水位lt、阀位Vt、疏水出口温度Tdo,t和给水出口温度Two,t的响应曲线,如图5所示。可以看出,水位可以快速地被调节至初始状态,且过程中阀门开度被限制在的软约束之内。在稳定状态下,分别将蒸汽压力从5.95 MPa升至6.45 MPa、将蒸汽温度从396 ℃升至400 ℃、将给水质量流量从417.5 kg/s升至422.5 kg/s、将给水入口温度从249.5 ℃升至251.5℃,观察各参数的响应曲线,如图6所示。可以看出,各边界条件不仅影响疏水和给水的出口温度,还改变了新稳态下的水位值,变化过程较快且没有出现超调。

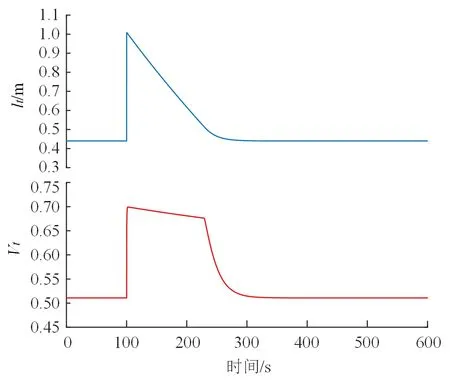
(a)水位和阀位的响应曲线

(a)Ps,t从5.95 MPa阶跃至6.45 MPa

从249.5 ℃阶跃至251.5 ℃为了进一步说明基于强化学习的性能最优控制框架得到的策略函数的合理性,将策略函数在对应工况下的稳定水位与试验最优水位进行对比。试验最优水位来自于APROS仿真模型的设定值试验优化[34],它是一种经典的工程优化方法,通过在试验中手动调整控制系统的设定值,以确定各边界条件下以性能指标为目标的最优设定值,并拟合最优设定值与各边界条件的关系曲线以参与控制。

图7给出了强化学习策略函数稳定水位与试验最优水位关于每个边界条件的特性对比情况。可以看出,基于强化学习的性能最优控制框架得到的策略函数在各工况下的稳定水位与设定值试验优化得到的最优水位比较接近,相对于边界条件的趋势也相似。在变蒸汽压力条件下,策略函数稳定水位和试验最优水位趋势存在差异。可以看出,试验最优水位的趋势比较平滑,而策略函数稳定水位的曲线在5.9 MPa附近存在一个拐点,可能的原因是策略函数采用了ReLU的隐层激活函数,导致其函数曲面不连续。可能的改进方法是减少策略函数层数,并使用平滑连续的激活函数。考虑到相关控制策略学习算法的特性,一般训练控制策略所使用数据的工况范围与其适用的工况范围是相近的,因此不建议在训练数据所在范围之外使用得到的控制策略。本文选择在THA稳定工况附近对模型的有效性进行了验证,而在范围外的实验效果不佳。

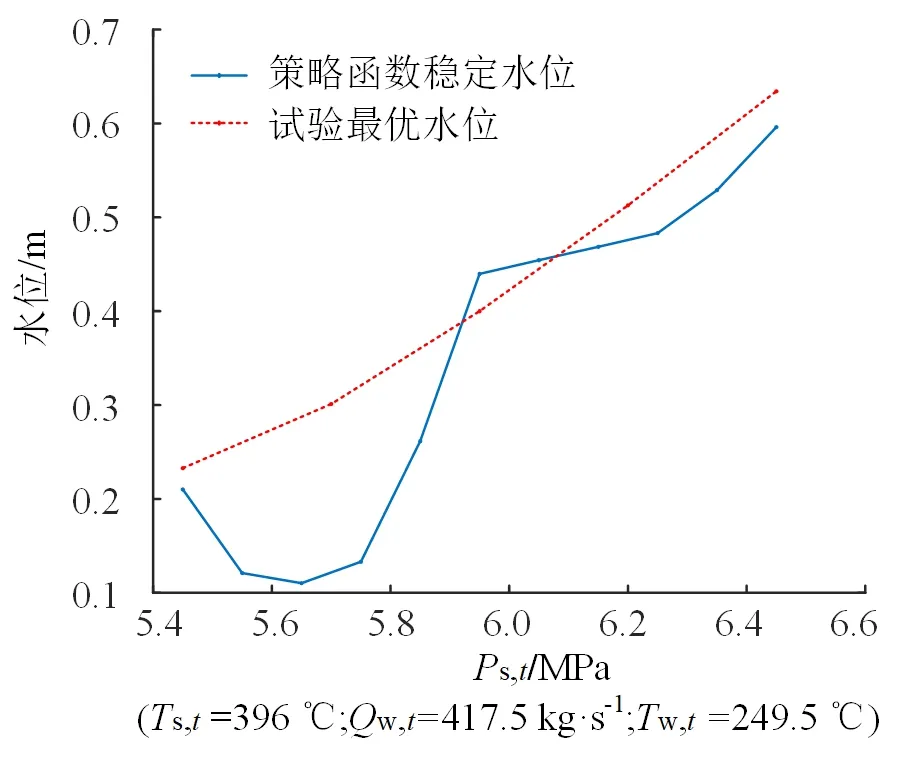
(a)不同Ps,t下策略函数稳定水位与试验最优水位对比

在实际应用中,设定值试验优化在面对多边界条件的场景时,需要进行大量的组合试验以确定各工况下边界条件与最优设定值的关系,而采用基于强化学习的性能最优控制框架可以直接利用历史运行数据求解控制策略函数,不仅在动态过程中可以达到较好的控制品质,稳态下也能使系统维持在性能较优的状态,相当于同时实现了设定值优化与设定点跟踪控制。然而,Q值函数存在近似误差,框架得到的策略函数尚达不到理论最优的控制品质。这是由于Q值本身是对单步状态转移的奖励估计,而优化目标是最大化多步累积奖励。采用机器学习算法拟合单步奖励必然会存在误差,在常规的监督学习任务中,这种误差的影响不大,而在强化学习任务中,单步误差的多步累积,可能导致多步优化目标存在较为明显的差异,因此得到的控制策略与解析法相比往往是次优的,但是其优势在于可以处理解析法无法解决的问题,对于解决包含复杂目标的过程控制任务具有较大的潜力。

5 结 论

考虑到火电厂对象特性复杂、动作空间维度较低、策略函数在训练期间无法与物理系统交互等特点,本文提出了基于强化学习的性能最优控制框架。在框架的数据预处理环节提出了HGA算法,以较低的计算负载解决了数据不平衡问题。在策略函数求解环节提出了PSO-CBQ算法,使用粒子群优化准确快速地实现了动作值迭代计算中的最大化运算,解决了连续动作强化学习求解效率低的问题。在高压给水加热器性能最优控制算例中,将基于强化学习的性能最优控制框架训练得到的策略函数与试验最优水位设定值控制器进行了对比。结果表明,基于强化学习的性能最优控制框架不需要建立系统模型,可以直接利用历史运行数据求解以累积性能最优为目标的控制策略函数,不仅在动态过程中可以达到较好的控制品质,稳态下也能使系统维持在性能较优的状态,相当于同时实现了设定值优化与设定点跟踪控制。