多孔型石英复合材料受热脱水特性的研究

透波材料是用于保护航天飞行器在极端环境下工作的一类多功能介质材料,主要应用于雷达、导弹、运载火箭或航天飞行器上的雷达罩及天线窗中。其中多孔型石英复合材料由于其质轻、比强度高、耐高温、透波性能好等优异特性,得到了普遍关注并被广泛应用

。然而,由于其多孔结构和存在亲水基团,材料在储存时会发生一定程度的吸潮。同时,由于水的介电常数和介电损耗很大(25 ℃时水介电常数约为76,介电损耗角正切约为0.2;多孔型石英复合材料介电常数约为3.7,介电损耗角正切约为0.005),吸潮后材料的介电常数和介电损耗急剧增大,雷达罩透波性能恶化,从而使得雷达作用距离大大缩短,瞄准误差增大

。飞行器在高超声速飞行中引起气动加热,内部水分分布发生急剧变化会导致材料介电性能的不稳定。

随着我国政府会计改革的不断深入推进，2017年10月24日，财政部印发《政府会计制度—行政事业单位会计科目和报表》（财会〔2017〕25号，以下简称《政府会计制度》），要求自2019年1月1日起全面施行，并鼓励行政事业单位提前执行。《政府会计制度》构建了“具备财务会计与预算会计双重功能，实现财务会计与预算会计适度分离并相互衔接”的全新政府会计核算模式，对会计科目的设置使用和报表格式及编制进行了详细说明，同时在附录中列示了主要业务和事项账务处理举例。

多孔材料内部的湿分传递过程较为复杂,不仅包括液态和气态湿分的流动,同时还包含扩散和相变过程,这对材料内部湿分分布和传递过程的有效预测带来了难度。早期的研究中只单独考虑多孔材料内部的湿分传递过程或热量传递过程,随着数值理论和对材料内部热量、湿分耦合传递机理探索的深入,目前多孔材料中湿分和热量的传递过程往往采用热-湿耦合传递模型进行研究

。Steeman等

建立了一种忽略材料内部湿分流动的多孔材料湿分和热量耦合传递模型,但是该模型在大温差和湿空气流速较高的情况下不能对材料中的温度、湿分进行准确预测。VAN Belleghem等

提出了一种同时考虑蒸气和液体湿分的热-湿耦合模型,该模型能够描述多孔建筑材料内的热-湿传递过程。Defraeye

建立了一种控制容积法和有限元法耦合求解多孔材料内部热-湿耦合传递的数值模型。何宣澄等

对建筑围护结构从初建成到湿稳定过程中的含湿量变化及湿积累进行研究,为更好控制建筑墙体保温层中湿积累的产生提供了参考。

二是要注重导向性。所谓导向性，就是将名师评选的条件和标准作为方向标、指挥棒，使每一个有志于成为名师的教师明确努力的方向。从加强教师队伍建设这个意义上讲，名师的评选既重在结果，同时也重在过程。从遴选指标体系各要素及其权重中，可以看出名师评选的导向性。

多孔材料的湿分传递过程包括吸湿过程和干燥脱水过程,对于干燥脱水问题而言,部分学者认为其实质就是获得空气和多孔材料界面的对流传质系数。Defraeye等

模拟了平板多孔材料干燥脱水过程,发现在干燥条件变化时表面对流传质系数会失效;Khan等

研究了苹果切片在不同边界条件下的干燥问题,所建隐式动态耦合模型可以准确预测不同气流速度下的干燥过程;Defraeye等

利用Comsol Multiphysics研究了苹果表面传热和传质系数,结果表明,当直接受到太阳辐射时,空气的流动有利于水果的冷却并能提高其干燥速率;Elhalwagy等

研究了苹果切片和矿物石膏表面的热量和质量传递过程,发现对于苹果干燥过程而言,传质阻力以材料侧的扩散阻力为主,而石膏干燥过程中的传质阻力主要为空气侧的对流阻力。以往学者提出的典型干燥理论可以概括为:Lewis提出的液态扩散理论认为,干燥过程中,固体材料内部湿分在湿度梯度的驱动下以液态扩散的形式进行迁移

;Henry提出的蒸发冷凝理论认为水分含量以蒸气的形式扩散,考虑了温度和质量的同步扩散过程,并且假设固体骨架分割成的孔隙均匀、连续;Gurr等通过实验证实,土壤等非饱和多孔介质在温度梯度下没有液体流动,湿分仅以蒸气的形式扩散

;Luikov

认为蒸气、空气和液态水分子的传质过程在干燥中同时发生,其中蒸气和空气以扩散、渗流或滤流的形式传递,液体的变迁以扩散、毛细吸附和滤流的形式进行;Krischer模型只考虑了第一类边界条件以及等温吸附曲线,而Abahri等在Krischer模型的基础上补充了质平衡方程,扩大了其应用范围

。

上述多孔介质内的干燥理论广泛应用于建筑材料及生物制品干燥过程研究,鲜有对于多孔透波材料高温受热条件下脱水过程的热湿耦合研究。为了探究含湿多孔型石英复合材料在受到高温加热时内部热量和湿分的传递规律,本文采用上述蒸发冷凝相关干燥理论,建立了多孔型石英复合材料热-湿耦合传递高温脱水数值模型。按照国际标准文件规定的杯法开展实验获得了多孔型石英复合材料的水蒸气阻力系数;设计并开展了多孔型石英复合材料高温加热实验,验证了数值模型的有效性;通过分析不同工况下材料内部温度、体积含湿量及介电损耗随加热时间的变化规律,探究了实际应用过程中,受热温度、材料初始含湿量、水蒸气阻力系数对多孔型石英复合材料热湿传递及透波性能的影响。本文实现了多孔型石英复合材料内部温度和湿分的有效预测,从而为该材料的实际使用提供了指导。

1 计算模型和数值方法

1.1 物理模型

为探究多孔型石英复合材料受高温加热脱水时内部热量和湿分的传递规律,进而在实际应用中减少在气动加热下石英复合材料中湿分剧烈变化对飞行器透波性能的影响,需建立多孔型石英复合材料热-湿耦合传递高温脱水的数值模型。

首先对该过程的物理模型进行分析与简化,多孔材料内部的热量和湿分传递与材料周围的湿空气的流动状态密切相关,其中热量的传递包括液态湿分、湿空气流动引起的对流换热、辐射、多孔骨架和孔隙中介质的导热以及由于水蒸气的冷凝、液态水的蒸发而导致的相变换热等;湿分的传递包括液态湿分的流动过程、水蒸气的扩散作用和水蒸气随空气流动引起的对流传质等过程。

本次实验采用的TGP 206A型地质超前预报仪对蓄集峡水电站引水发电隧洞进行超前地质预报，由于该仪器具有非常高的灵敏度，因此在每次进行实验开始之前，能够产生震动的一切施工工作均暂停，以防影响数据采集；而在两个接收孔中采用黄油将两个接收探头与山体耦合；炮孔间距为2 m，深度为2 m，下倾10°左右以方便注水，炸药放置时应当将炸药推入炮孔底部，在入洞之前将药卷制作完成以节省时间；当仪器连接完成之后，采用逐一引爆的规则，按顺序引爆并收集信号，若有哑炮或未触发的情况时，应当补炮，不能直接跳过。因为药卷的引爆和信号的采集应当同时进行，故药卷应当与触发线连接。

借助Ansys ICEM CFD工具建立了三维网格模型,为减少计算量,采用1/4对称模型,网格按1∶1大小取材料及周围湿空气区域的四分之一为建模区域。在Fluent中按照前述的控制方程自编程UDF进行模拟,边界条件设置为实验真实环境所对应的参数,即空气区域远场设置为296 K、相对湿度为72%的定温定湿度边界,样品加热面设置为定壁温加热,该壁面绝湿。样品初始湿分设置为24.6 g,壁面加热温度按照实验所测得加热面温度曲线设置。经过网格和时间无关性检验,结果如图5所示,采用网格个数384 345,时间步长为1 s。

1.2 数学模型

1.2.1 湿空气区域

强化专项整治，严厉打击食品药品安全违法行为。积极开展各类食品药品专项整治工作，加大对重点产品、重点区域、重要节点的食品专项整治，如豆制品专项整治、疫苗专项整治等。专项检查组共出动人员82人次，执法车辆22车次，对辖区内2家药品批发企业、3家有接种资质的医院、17家疾控中心、3家有接种资质的社区卫生室进行了全面检查。创新宣传形式，全面推进社会共治。通过开展各类宣传，有组织、有计划、有步骤地开展食品药品安全宣传活动；加大对企业责任人的培训工作，提升企业第一责任人意识和自律意识。

真实使用环境下多孔型石英复合材料内部湿分迁移和能量传递包含化学反应、导热传热、辐射传热等多种方式的结合,并且内部多孔材料还需要与外部湿空气区域进行传热传质的界面耦合,直接建立这样的多孔型石英复合材料传热预测模型具有较大的难度。相较于湿空气区中的液态水,本研究更关注气态水的扩散和对流,因此采用以下假设:没有化学反应,忽略水蒸气的冷凝;干空气和水蒸气视为理想气体,干空气的比热容视为定值;输运过程湿空气压力变化较小,不会影响湿空气的热物性。可得湿空气区的连续方程以及动量方程

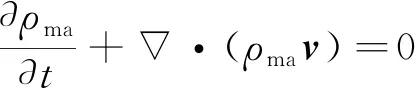
(1)

(2)

式中:

为湿空气的密度,kg/m

;

为动力黏度,Pa·s;

为时间,s;

为速度,m/s;

为压力,Pa。

盾遂奔，未出晋境。……晋太史董狐书曰“赵盾弑其君”，以视于朝。盾曰：“弑者赵穿，我无罪。”太史曰：“子为正卿，而亡不出境，反不诛国乱，非子而谁？”孔子闻之，曰：“董狐，古之良史也，书法不隐。宣子，良大夫也，为法受恶。惜也，出疆乃免。”(《晋世家》)

根据相变传质Lee模型

,相变质量源项

的计算式为

(3)

式中:

为湿空气区域含湿量,即单位体积内的水蒸气质量,kg/m

;

为水蒸气扩散通量,kg/(m

·s);

为水蒸气质扩散系数,m

/s。

式(3)表示在单位时间内单位控制体中,水蒸气质量分数的增加量与通过边界流出控制体的水蒸气质量之和,等于通过边界扩散进入的水蒸气质量。为了考虑温度变化对水分输运产生的影响,需要建立能量方程。依据1

2

1节中的假设,按照与湿分输运方程相同的分析方法可以推导得到湿空气的能量方程

西王集团以玉米深加工和特钢为主业，拥有三家上市公司，其成长历程堪称改革开放40年中的标志性企业。其创始人王勇是全国人大代表，也在今年入选改革开放40年感动山东人物。

式(4)表示在单位时间单位控制体中,湿空气能量的增量与控制体边界流出湿空气带走的能量之和,等于通过控制体边界导入的能量与控制体边界水蒸气扩散带入的能量之和。干空气和水蒸气的焓值可以视为热力学温度的线性函数,故将水的气化潜热视为常数。

(4)

(5)

式中:

为比热容,J/(kg·K);

为热力学温度,K;

为湿空气导热系数,W/(m·K);下标ma表示湿空气,vap表示水蒸气,air表示干空气。

1

2

2 多孔材料区域

不考虑化学反应过程,多孔型石英复合材料内的湿分主要以液态吸附水和气态水蒸气两种形式存在。多孔型石英复合材料内部孔隙尺度较小,因此可以忽略其中的对流传热过程。根据所模拟材料中水分转移方式的不同,部分学者将多孔材料中的热-湿耦合模型分为两类,一些模型认为水蒸气输运是唯一的水分输运机制,而另一些模型则同时考虑水蒸气输运和液体输运

。基于蒸发冷凝理论,认为非饱和多孔介质在温度梯度下没有液体流动,湿分仅以蒸气形式扩散

。在文献[17]中,采用临界含湿量的概念区分蒸气主导的湿分输运与液体主导的湿分输运。对于吸湿性多孔材料,当相对湿度低于98%时,材料内部水分迁移过程中,水蒸气扩散将占主导地位

,并可以用水蒸气阻力系数涵盖液体输运的较小贡献。基于以上分析并采用蒸发冷凝理论,作如下假设:孔隙中水蒸气仅以扩散形式发生迁移;由于多孔型石英复合材料在常温存储状态下吸湿,相对湿度低于临界状态,并且加热过程中升温较快,液态水蒸发后的蒸气输运占主导作用,可以认为液态水牢牢附着在多孔材料表面,毛细力导致的液态水迁移过程可以忽略;低于相变温度时,材料内部液态水的蒸发和水蒸气的冷凝过程可以忽略;仅考虑多孔材料内部湿分的相变吸热反应,忽略其他化学反应过程。可得多孔区域的连续方程以及动量方程

(6)

此模块包含视频信息的增删查改功能。点击新增链接，在弹框中输入章节、名称、简介、视频链接后提交，页面刷新后在列表中即可找到刚刚新增的视频；在APP视频列表中亦能找到对应的视频，还能对视频列表中的视频元素进行编辑和删除。

(7)

式中

为质量源项。

多孔型石英复合材料加热至1 000 s时的仿真结果如图8所示,随着加热的不断进行,热量由样品底部迅速向上传递,样品的温度逐渐达到相变温度并且液态水剧烈相变反应的区域产生了大量气态水,气态水向材料开放壁面逃逸形成蘑菇云状的分布,浓度依然呈现出从相变区域向样品四周递减的规律。仿真结果与物理过程一致,可以认为本文构建的多孔型石英复合材料在受热下脱水过程的仿真模型较准确可靠。

(8)

液态水输运方程

(9)

式中:

为孔隙率;

、

分别为材料孔隙中水蒸气、液态水质量浓度,即单位材料孔隙体积内的水蒸气和液态水质量,kg/m

;

为水蒸气在空气中的扩散系数,m

/s;

为水蒸气在多孔材料中的无量纲扩散阻力系数,其含义为水蒸气在湿空气中的质扩散系数与多孔材料中的质扩散系数之比;

为相变质量源项。

（51）三願九祖盡生天，四願酆都皆罷對。五願二炁無愆伏，六願五穀悉酆登。（《北極真武佑聖真君禮文》，《中华道藏》30/590）

通过引入水蒸气阻力系数

,将多孔材料内部的湿分扩散表示为水蒸气在湿空气中的扩散。水蒸气阻力系数

(

)与多孔材料自身特性有关,一般通过实验或查阅手册获得。

以包含固相、液相和气相的REV为研究对象,由于忽略了液态水和湿空气的流动,能量的变化仅由导热、水蒸气的扩散及蒸发等引起。根据控制容积分析法可得多孔材料中的能量方程

(10)

(11)

(12)

式中:

、

和

分别为干燥多孔材料、水蒸气和液态水的比热容,J/(kg·K);

为多孔区域总的体积含湿量,kg/m

;

为考虑含湿和辐射热导率影响的多孔材料的等效热导率,W/(m·K);

为相变潜热,J/kg。

由控制方程可知,多孔材料中的温度会影响水蒸气和液态水的相平衡,因此多孔材料中的湿分输运方程和能量方程需要耦合求解。

1.3 模型关键参数获取方法

为建立上述数值模型,模型中的一些关键参数需通过经验公式确定或实验测得,包括相变质量源项

、水蒸气在空气中的扩散系数

、多孔型石英复合材料的水蒸气阻力系数

、材料初始含湿量

及材料各物性参数。

为了模拟湿空气中的水分输运,根据水蒸气的质量守恒引入了湿分(湿空气中仅指水蒸气)输运方程。水蒸气在湿空气中的输运包含了因流动和扩散而引起的质量传递,其中扩散可以通过Fick定律来进行描述。通过控制体分析的方法得到湿空气中水蒸气的输运方程

(13)

式中:

为Lee模型的质量交换系数,s

;

为含湿多孔型石英复合材料内部液态水相变的反应温度,可以借助同步热分析仪实验测试得到。

水蒸气在空气中的扩散系数

可根据Fuller公式

确定

(14)

式中:

为绝对压力;

为摩尔质量,g/mol;∑

为对应组分的扩散体积,cm

·mol

;∑

HO

=13.1 cm

/mol,∑

=19.7 cm

/mol。

【子棱被士兵们裹挟着往前走，蓦地，他奋力地往回冲，被士兵挡住，突然全场定格，鸦雀无声，只有子棱的声音在空中回响，那声音很慢很慢。

多孔型石英复合材料的水蒸气阻力系数(水蒸气在湿空气中的质扩散系数与多孔材料中的质扩散系数之比)由杯法实验获得,如图1所示。根据2016年的ISO12572标准

,在杯中装入一定量干燥剂(干杯)或饱和盐溶液(湿杯),保持干杯或湿杯中相对湿度的恒定,并将样品密封于测试杯中,然后将实验装置置于温度和湿度维持恒定的恒温恒湿箱中。由于恒温恒湿箱和杯中的水蒸气分压力不同,水蒸气将会从分压力高的一侧向另一侧扩散,待水蒸气在多孔样品中的流动达到定常状态后,称量装置的质量变化率,即为多孔材料的水蒸气流率。然后利用该值可以计算得到水蒸气阻力系数

,具体计算公式为

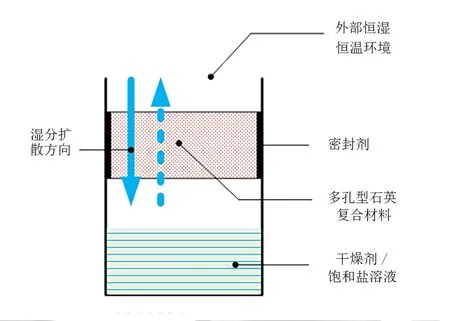
(15)

=

(16)

(17)

式中:

为水蒸气渗透力,kg/(m

·s·Pa);

为通过样品的水蒸气流率,kg/s;

为样品有效横截面积,m

;Δ

为样品两端水蒸气压差(通过温度和相对湿度计算),Pa;

为多孔样品的厚度,m;

为多孔材料的透湿性,kg/(m·s·Pa);

为空气透湿性,kg/(m·s·Pa)。

在293 K、57%相对湿度环境下,根据杯法实验得到多孔型石英复合材料的水蒸气阻力系数

=35

3。假定初始状态下含湿多孔型石英复合材料内部的水蒸气和液态水处于平衡状态,则初始时刻的

、

满足以下关系

(18)

多孔型石英复合材料的其他物性参数分别为:

=0

3,

=1 700 kg/m

,

=0.8 W/(m·K),

=828 J/kg。

式中:

为材料初始含湿量,由实验测得给出;

为干燥多孔型石英复合材料密度,kg/m

。

1.4 数值求解

采用流体力学计算软件Ansys Fluent 18.0求解多孔区域和湿空气区域的控制方程,其中连续性方程、动量控制方程通过求解器默认的连续方程、动量方程进行求解,由于湿空气区域和多孔区域中能量方程的复杂性,能量方程采用自定义形式。通过引入3个自定义标量(user-defined scalar,UDS),分别代表水蒸气浓度

、液态水浓度

和温度

,编写用户自定义程序(user-defined function,UDF)对两区域内部的湿分输运方程和能量方程进行求解,具体数值求解计算流程如图2所示。

“不行！”叶晓晓还是斩钉截铁。她有自己的小九九，偶尔玩玩，展示一下自己的身材，是可以的，但要真拍了照片，一张一张复制出去，那后果不是自己能控制的。

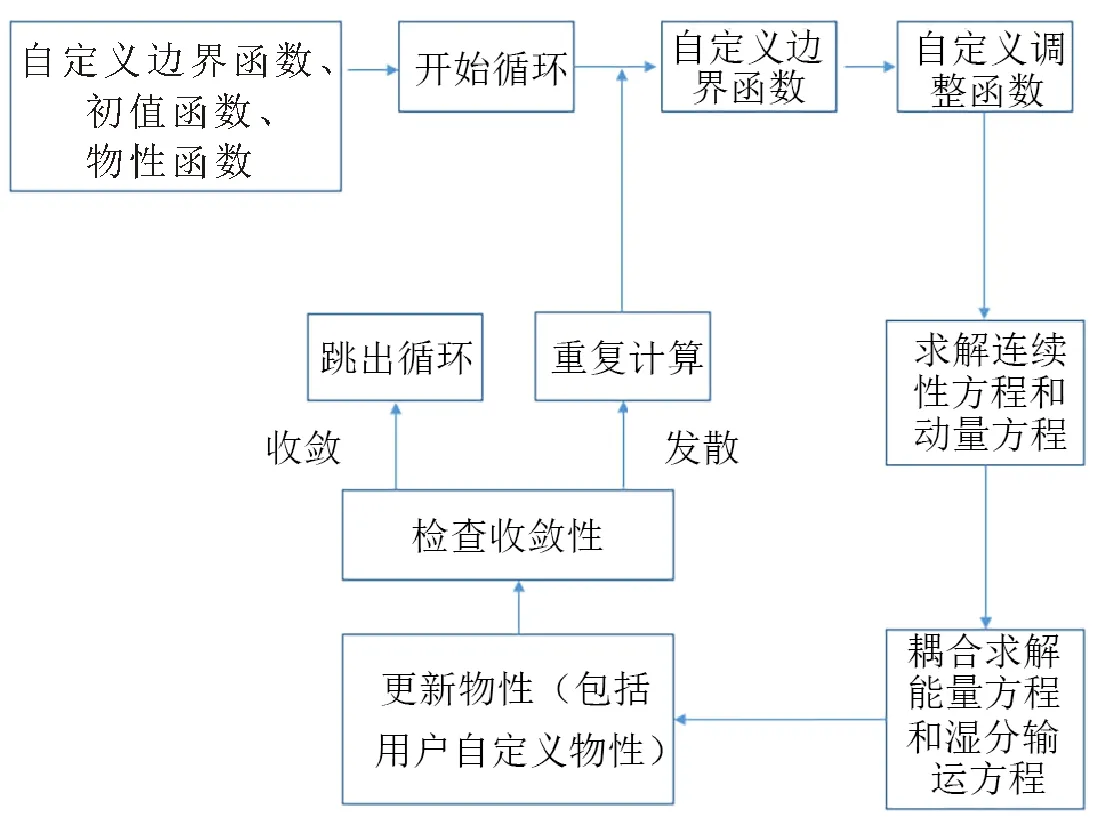
界面耦合处理过程如图3所示,其中

、

、

分别表示空气侧体网格温度、多孔侧体网格温度、界面温度,

、

分别表示界面两侧相邻的空气侧体网格到界面的距离、多孔侧体网格到界面的距离,

、

分别表示空气侧体网格热导率、多孔侧体网格热导率,

表示热流。与之相对应的,

、

、

分别表示空气侧体网格水蒸气浓度、多孔侧体网格水蒸气浓度、界面水蒸气浓度,

、

分别表示空气侧体网格的水蒸气扩散系数、多孔侧体网格的水蒸气扩散系数,

表示湿分运输通量。由于上述物理过程满足界面处的温度连续、热流连续、水蒸气浓度连续、湿分运输通量连续4个条件,且湿空气区与多孔区的控制方程实质相同,故模拟过程中将其界面作为内部面直接处理,两侧调用空气、多孔的不同物性参数及物理量进行直接耦合计算,湿分的传递过程类比热量的传递进行耦合处理。

采用Simple算法对多孔及湿空气区域的热-湿耦合过程进行求解,非稳态项采用一阶隐式格式离散,压力采用二阶格式进行离散,动量、速度、温度和体积含湿量均采用二阶迎风格式进行离散。

谈及设备的配备，张军表示，这也是2008年—2013年报业印刷最辉煌时期的映射。如今，受互联网、移动阅读等的冲击，整个传统媒体的市场空间明显收缩，纸媒亦难以独善其身，都市类报纸发行量下降幅度较大。

2 模型验证

由于开展含湿多孔型石英复合材料在高马赫数下气动加热的脱水过程研究需要较大的风洞设备,实验条件复杂且苛刻,故将材料的气动加热简化为壁面加热。为研究含湿多孔型石英复合材料在受热脱水过程中,材料内部水分分布随时间的变化过程,并验证已建立的多孔型石英复合材料在受热条件下脱水过程的数值模型,构思并设计了验证实验方案,搭建了壁面加热实验装置,其中包括秤盘及称量传感器、隔热瓦、加热器及相关热电偶接线,热电偶布置点位示意图如图4所示。

进行了423 K加热实验,所采用的多孔型石英复合材料如图4所示,其干质量为394.73 g,长115 mm、宽78 mm、高25 mm,脱水前已于293 K、相对湿度80%温湿环境中吸湿至饱和质量421.16 g,实验时空气环境温度为296 K,相对湿度为72%。

由于湿分在湿空气和多孔型石英复合材料中的存在状态以及传递过程有较大的差异,所以需要对空气和多孔材料中的传热传质过程分析并建立相应数学模型。

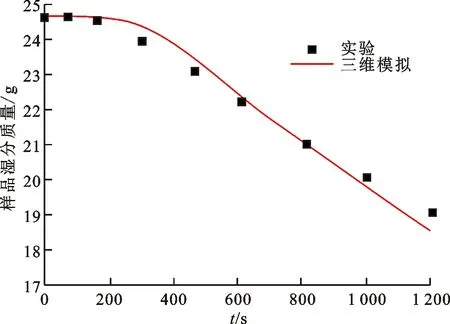
多孔型石英复合材料在加热温度为423 K时的高温脱水实验获得的样品侧面中心处温度与上述仿真结果的对比如图6所示,仿真结果与实验结果的相对误差小于5%。将423 K高温脱水实验获得的样品质量变化曲线与上述仿真结果对比,如图7所示,可知三维模拟结果与实验数据符合较好,仿真结果与实验结果的相对误差小于5%。

根据Whitaker体积平均理论

,在表征体元(representative elementary volume,REV)尺度建立多孔区域的水蒸气输运方程

（1）要完善中小学财务管理的内控制度，最为紧迫的是建立学校财务管理的预算制度，其中关键是要选择更加详细更加合适的编制预算的方法，充分考虑中小学的机构设置、人员编制、学生和班级数量、经费控制标准及发展的方向；同时，为确保财务制度得到全面落实，应该严格执行下达的预算，不能出现超总额超定额的现象。以学校的物资采购为例，对学校办公用品、教学仪器、文体器材等采购时，不仅采购流程要严格执行相关规定，还必须做到：一方面，财务部门对每一笔支出的合理性进行分析，以确保预算资金的合理使用；另一方面，应完善票据管理方法，对发票、附件等进行核查，确保其真实合法性。

3 结果讨论与分析

为了近似探究实际应用过程中,材料受热脱水时,受热温度、材料初始含湿量、水蒸气阻力系数对多孔型石英复合材料热湿传递及透波性能的影响,使用本文构建的多孔型石英复合材料在受热下脱水过程的热-湿耦合传递模型,分析了不同工况下材料内部温度、体积含湿量及介电损耗随加热时间的变化规律。

3.1 加热温度对多孔型石英复合材料受热脱水历程的影响

合作单位提供了两种不同形状的多孔型石英复合材料,除上述验证实验中的长方体样品,还有如图1所示的圆柱体样品,其直径为25.44 mm,高为20 mm。由于长方体三维模拟耗时较久,为简化计算,采用轴对称圆柱多孔型石英材料使用相同程序进行模拟,轴对称模型网格划分示意图如图9所示。圆柱体轴对称模拟网格无关性检验如图10所示,在保证计算精度的前提下优化网格,最终采用网格数为40 991。设置初始条件是:空气域初始温度为296 K,初始相对湿度为72%,边界条件为远场绝热、绝湿边界,材料下壁面为定壁温加热、绝湿边界。

图11、图12为不同加热温度工况受热脱水时体积含湿量随时间变化曲线和不同加热温度工况受热脱水时平均温度随时间变化曲线,可知随着壁面加热温度的升高,材料升温速率显著变快,材料脱水速度也显著增加,当523 K加热工况脱水结束时,423 K加热工况仅脱除约三分之一湿分。

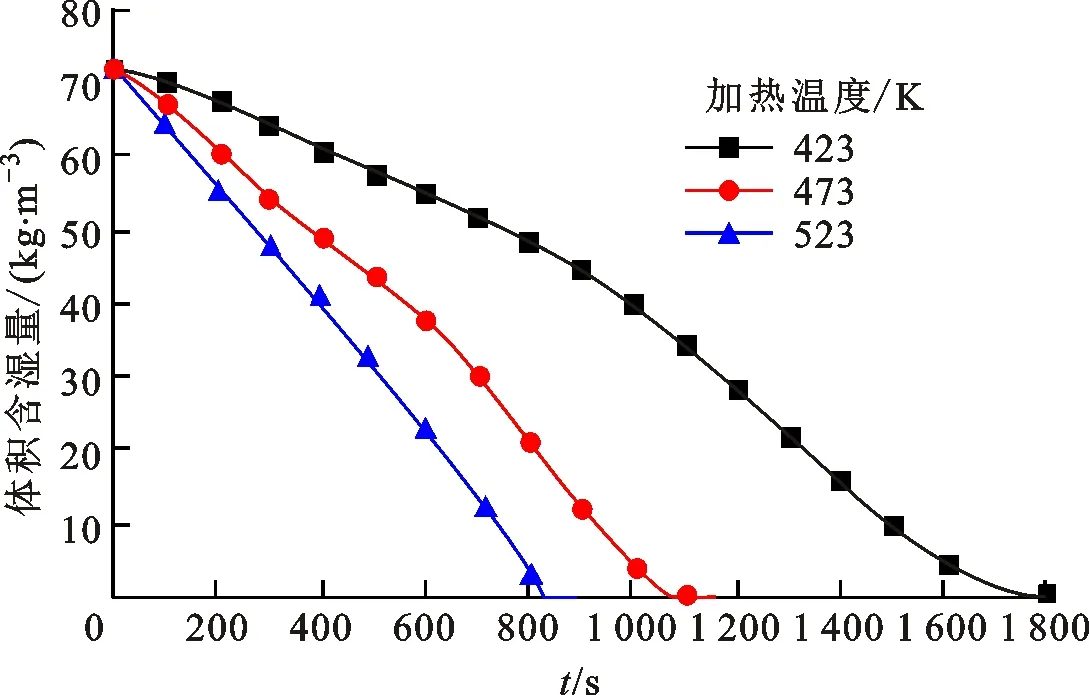
图13为不同加热温度工况受热脱水时平均介电损耗tan

随时间变化曲线,材料贮存吸湿后其中的水分会增加材料整体介电损耗,观察到随着时间的推移加热脱水过程不断进行,材料的平均介电损耗也随之降低。由于较高的加热温度会导致水分脱除的较快,材料的平均介电损耗减小速率也较大,水分对材料透波性能的影响消除得更快。

3.2 材料初始含湿量对多孔型石英复合材料受热脱水历程的影响

图14、图15为不同初始含湿量工况受热脱水时,材料体积含湿量及平均温度随时间变化曲线。其中5 kg/m

、15 kg/m

、72 kg/m

工况分别对应材料于303 K温度下相对湿度30%、60%、90%时环境中储存所得饱和吸湿工况。由图14可以看出,初始含湿量对脱水过程影响较大,初始含湿量越大,所需高温加热时间越长,初始含湿量为72 kg/m

时的脱水时间约为5 kg/m

工况的1.9倍。由图15可以看出,不同初始含湿量对材料平均温度变化的影响较小,15 kg/m

、5 kg/m

工况升温情况几乎相同,72 kg/m

工况由于含湿量较高,脱水时湿分相变吸收大量热量,导致升温速率较慢。

图16为不同初始含湿量工况受热脱水时材料平均介电损耗tan

随时间变化曲线,观察到由于初始含湿量较大,72 kg/m

工况的平均介电损耗始终高于5 kg/m

工况,并且由于初始含湿量越高的工况完全脱除水分的时间越长,其平均介电损耗变化时间持续更久。

课程可以分为理论课程和实践课程，而普通高校比较擅长于理论课程的讲授，而容易忽视实践课程的教学，导致部分社区成员社区学习的兴趣不大。社区成员迫切需要的保健、家政、阅读、休闲和提高交往能力的课程，普通高校往往因认识角度问题而认为不重要，不予开设。

3.3 水蒸气阻力系数对多孔型石英复合材料受热脱水历程的影响

图17、图18为不同水蒸气阻力系数工况受热脱水时材料平均气态水浓度及液态水浓度随时间变化曲线,可知随着水蒸气阻力系数的增大,其对相变得到的气态水逸出有明显的阻碍作用,而对相变过程几乎无影响。含湿多孔型石英复合材料在受热时的脱水过程要综合液态水的相变和气态水的扩散作用,当水蒸气阻力系数达到200且远远高于材料实际水蒸气阻力系数时,对总体积含湿量的影响仍然很小,可以认为水蒸气阻力系数对材料的高温脱水过程影响有限。

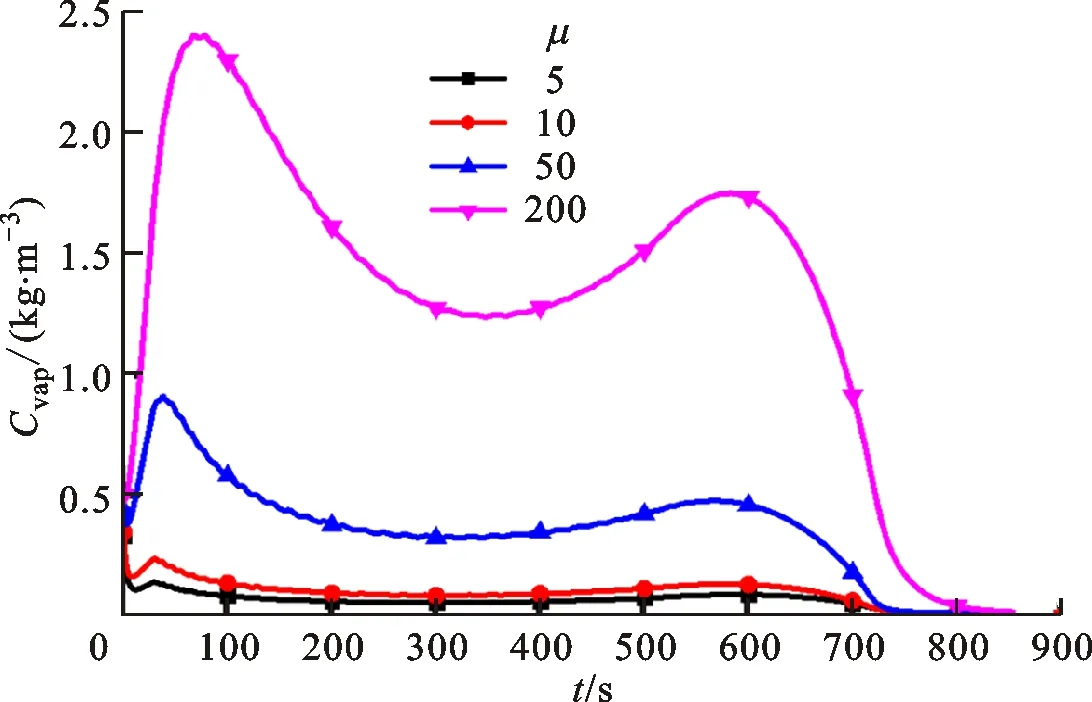
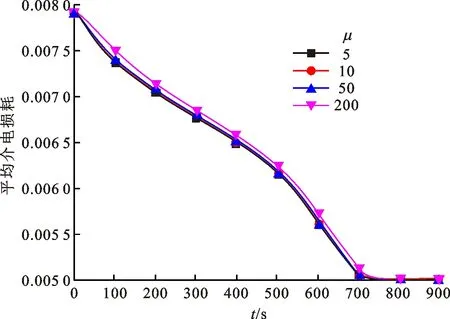
图19为不同水蒸气阻力系数工况受热脱水时材料平均介电损耗随时间变化曲线,观察到水蒸气阻力系数越大的工况,其平均介电损耗tan

也越大,但当水蒸气阻力系数达到200且远高于材料实际水蒸气阻力系数时,对总体积含湿量的影响仍然很小,这就导致其对介电损耗的影响也很小,可以认为水蒸气阻力系数对材料的高温脱水过程中材料介电损耗影响有限。

4 结 论

本文针对含湿多孔型石英复合材料受热脱水影响透波性能的问题,建立了热-湿耦合传递高温脱水数值模型,开展了关键参数对脱水过程影响的分析,获得了受热脱水过程中材料温度、湿分及介电损耗的分布,可得如下结论。

(1)建立了多孔型石英复合材料高温脱水过程的热湿耦合模型,通过杯法实验获得了其中的关键输入参数,即水蒸气阻力系数

,293 K、57%相对湿度环境下测得多孔型石英复合材料

=35.3。通过实验验证了所建热湿耦合模型的有效性,误差小于5%,该模型可有效预测加热条件下材料脱水过程的湿分、温度分布以及透波性能。

(2)探究了加热温度对多孔型石英复合材料受热脱水历程的影响。随着壁面加热温度的升高,材料升温速率显著变快,材料脱水速度也明显增加,含湿石英复合材料的介电损耗迅速降低。材料523 K加热工况下的脱水速度约为423 K下的3倍。在低空阶段充分加速以提高气动加热的温度及时间从而快速脱除湿分,减小高空飞行中湿分对无线电通信的影响。

(3)探究了材料初始含湿量对多孔型石英复合材料受热脱水历程的影响。初始含湿量越高,材料脱除水分所需的时间越长,并且脱水时湿分相变吸收大量热量,导致升温速率较慢,此时含湿石英复合材料的介电损耗较大并且下降较慢。环境温度为303 K时,90%相对湿度饱和吸湿工况脱水时间约为30%相对湿度工况的2倍。实际存储过程中应采取隔湿外涂层处理以减少其吸潮现象。

(4)探究了材料水蒸气阻力系数对多孔型石英复合材料受热脱水历程的影响。随着水蒸气阻力系数的增大,其对气态水逸出有明显的阻碍作用,而对液态水脱除几乎无影响,综合考虑认为水蒸气阻力系数

<200时,对材料的高温脱水过程影响有限,因此对含湿石英复合材料的透波性能影响也较小。

通过本文建立的多孔型石英复合材料热-湿耦合传递高温脱水数值模型,可以有效预测材料的湿分分布,进而判断材料的透波性能变化,研究结果可为该材料的实际应用提供指导。

:

[1] 何燕飞, 龚荣洲, 何华辉. 双层吸波材料吸波特性研究 [J]. 功能材料, 2004, 35(6): 782-784.

HE Yanfei, GONG Rongzhou, HE Huahui. Research on absorpting properties of double-layer absorpting materials [J]. Journal of Functional Materials, 2004, 35(6): 782-784.

[2] 李俊生, 张长瑞, 王思青, 等. SiO

/(Si

N

+BN)透波材料表面涂层的防潮性能和透波性能研究 [J]. 涂料工业, 2007, 37(1): 5-7, 10.

LI Junsheng, ZHANG Changrui, WANG Siqing, et al. Study on moisture-proof and wave-transimissivity properties of the coatings on SiO

/(Si

N

+BN) radome materials [J]. Paint & Coatings Industry, 2007, 37(1): 5-7, 10.

[3] STEEMAN H J, VAN BELLEGHEM M, JANSSENS A, et al. Coupled simulation of heat and moisture transport in air and porous materials for the assessment of moisture related damage [J]. Building and Environment, 2009, 44(10): 2176-2184.

[4] VAN BELLEGHEM M, STEEMAN M, JANSSEN H, et al. Validation of a coupled heat, vapour and liquid moisture transport model for porous materials implemented in CFD [J]. Building and Environment, 2014, 81: 340-353.

[5] DEFRAEYE T. Convective heat and mass transfer at exterior building surfaces [D]. Leuven, Belgi⊇: Katholieke Universiteit Leuven, 2011.

[6] 何宣澄, 孔凡红, 刘倩, 等. 热湿耦合作用下新建墙体保温层湿积累研究 [J]. 热科学与技术, 2020, 19(6): 588-592.

HE Xuancheng, KONG Fanhong, LIU Qian, et al. Study on moisture accumulation of new wall insulation layer under the coupled action of heat and moisture [J]. Journal of Thermal Science and Technology, 2020, 19(6): 588-592.

[7] DEFRAEYE T, BLOCKEN B, CARMELIET J. Analysis of convective heat and mass transfer coefficients for convective drying of a porous flat plate by conjugate modelling [J]. International Journal of Heat and Mass Transfer, 2012, 55(1/2/3): 112-124.

[8] KHAN F A, STRAATMAN A G. A conjugate fluid-porous approach to convective heat and mass transfer with application to produce drying [J]. Journal of Food Engineering, 2016, 179: 55-67.

[9] DEFRAEYE T, RADU A. Convective drying of fruit: a deeper look at the air-material interface by conjugate modeling [J]. International Journal of Heat and Mass Transfer, 2017, 108: 1610-1622.

[10] ELHALWAGY M M, STRAATMAN A G. Dynamic coupling of phase-heat and mass transfer in porous media and conjugate fluid/porous domains [J]. International Journal of Heat and Mass Transfer, 2017, 106: 1270-1286.

[11] LEWIS W K. The rate of drying of solid materials [J]. The Journal of Industrial & Engineering Chemistry, 1921, 13(5): 427-432.

[12] 杨明. 多孔介质热质传递耦合形式分析 [D]. 昆明: 昆明理工大学, 2017.

[13] LUIKOV A V. Heat and mass transfer in capillary-porous bodies [J]. Advances in Heat Transfer, 1964, 1: 123-184.

[14] ABAHRI K, BELARBI R, TRABELSI A. Contribution to analytical and numerical study of combined heat and moisture transfers in porous building materials [J]. Building and Environment, 2011, 46(7): 1354-1360.

[15] STEEMAN H J. Modelling local hygrothermal interaction between airflow and porous materials for building applications [D]. Ghent, Belgium: Ghent University, 2009.

[16] 巫恋恋. 装配式建筑连接节点热湿耦合传递研究 [D]. 天津: 天津大学, 2020.

[17] DE WIT M. Warmte en Vocht in Constructies [M]. Eindhoven, Holland: Eindhoven University of Technology, 2002.

[18] WHITAKER S. Simultaneous heat, mass, and momentum transfer in porous media: a theory of drying [M]∥HARTNETT J P, IRVINE T F. Advances in Heat Transfer. Amsterdam, Holland: Elsevier, 1977: 119-203.

[19] LEE W H. A pressure iteration scheme for two-phase flow modeling [M]∥Computational Methods for Two-Phase Flow and Particle Transport. Trenton, NJ, USA: World Scientific, 1980: 61-82.

[20] Anon. A new method for prediction of binary gas-phase diffusion coefficients [J]. Vacuum, 1966, 16(10): 551.

[21] ISO. Hygrothermal performance of building materials and products: determination of water vapour transmission properties: cup method: ISO 12572: 2016 [S]. Geneva, Switzerland: ISO, 2016.