某型火箭发动机涡轮转子流热固耦合强度及疲劳寿命分析

黄朝晖,袁奇,张弘斌,李浦,王振,黄道琼

(1.西安交通大学能源与动力工程学院,710049,西安;2.陕西省叶轮机械及动力装备工程实验室,710049,西安;3.中航科技集团航天六院西安航天动力研究所,710100,西安)

涡轮泵是液体火箭发动机的关键部件,它将液体氧化剂和燃料送入燃烧室,为火箭提供升力[1]。涡轮转子需要承受高温、高压和高转速的恶劣工作条件,所以火箭发动机的故障大多为涡轮泵所致。

文献[2]中建立了涡轮盘动力学模型,分析结构所承受的各种载荷对其振动模态特性的影响,最后对轮盘结构的振动安全性进行评估。文献[3]中针对某火箭发动机中高压液氧涡轮泵离心轮的前、后凸肩动密封,采用孔型/蜂窝阻尼密封代替原始迷宫密封方案,并开展了密封结构参数优化设计和封严性能分析研究。文献[4]中基于CFD分析技术和气动优化算法,开展了液体火箭发动机涡轮气动优化数值研究。

某国产液体火箭发动机涡轮泵[5]在试车试验中转子叶片型底前尾缘处萌生裂纹,为确定裂纹萌生的原因,需对涡轮转子进行各时刻气动、强度、振动三维有限元计算分析[6],包括其气动压力、温度分布[7],分别计算离心力、气动压力和热应力对涡轮叶片强度的影响,计算难点是火箭发动机启停工况的瞬态流动、传热的温度场、应力场计算,使用的关键技术是采用ANSYS流热固耦合有限元计算方法。

双向耦合分析比单向耦合分析[8]复杂得多,本文采用的ANSYS流热固耦合计算方法为双向耦合分析法。首先,双向耦合分析都是瞬态分析,除了对流固单独设置瞬态分析特性外,还需统一二者的时间步,保证时间步统一,文中考虑了启停工况各关键时间点的流动、传热、瞬态温度场、转速的互相影响;再者,双向耦合分析需要考虑大变形问题,以及大变形带来的网格问题,虽然可以通过“流场域切分法”、“网格重构”以及其他手段帮助解决,但是在高度非线性问题和大变形问题中,双向耦合分析的应用不是很普遍,本文在分析涡轮叶片产生裂纹原因上使用的ANSYS流热固耦合计算方法有一定的创新性。

1 研究方法及模型

1.1 实验测量方法

本文使用锤击法进行涡轮转子模态敲击实验[9],测量涡轮转子的固有频率。先将涡轮转子悬挂,然后使用带有力传感器的力锤敲击涡轮转子,产生的电压响应信号经过电荷放大器放大后与加速度传感器产生的响应信号一起传入动态采集仪Focus Ⅱ,最终动态分析仪根据程序LMS Test.Lab 17对所得激振信号进行分析后得出结果。

实验中使用江苏联能公司生产的LC-04A力锤敲击实验转子产生激励,力锤需要与CL-YD-305A型力传感器配套使用。该力传感器的最大量程为60 000 N,灵敏度为3.89 pC/N。实验中使用的单向加速度传感器为PCN公司生产的333B30型加速度传感器,采用压电式,精度为100 mV/g,工作温度为-18～66 ℃,实验室环境温度为16 ℃。

1.1.1 高周疲劳寿命评估

涡轮叶片作为火箭发动机的关键部件,在正常工作时需要承受波动的高压、高温和高转速,由空气动力学引起的高频振动容易导致涡轮叶片发生高周疲劳失效[10-12]。

本文计算涡轮叶片在等效非对称疲劳循环载荷下的疲劳极限时,采用Goodman修正公式[13]

(1)

式中:σ-1,eff为非对称循环下疲劳极限;σm为疲劳分析平均应力;σ-1为对称循环下疲劳极限;σb为材料抗拉强度。高周疲劳安全系数计算公式为

(2)

式中σa为交变应力幅值。

计算时分别采用材料验收性能参数值和协议性能参数值。协议性能参数值为材料按制造标准的各项规定参数值,主要包括条件屈服极限σ0.2、抗拉强度σb、距长度5倍直径的伸长率δ5和断面收缩率ψ;验收性能参数值为材料实际的各项参数值。涡轮转子叶片使用的材料为GH4586,材料GH4586协议值和验收值的力学性能如表1所示。

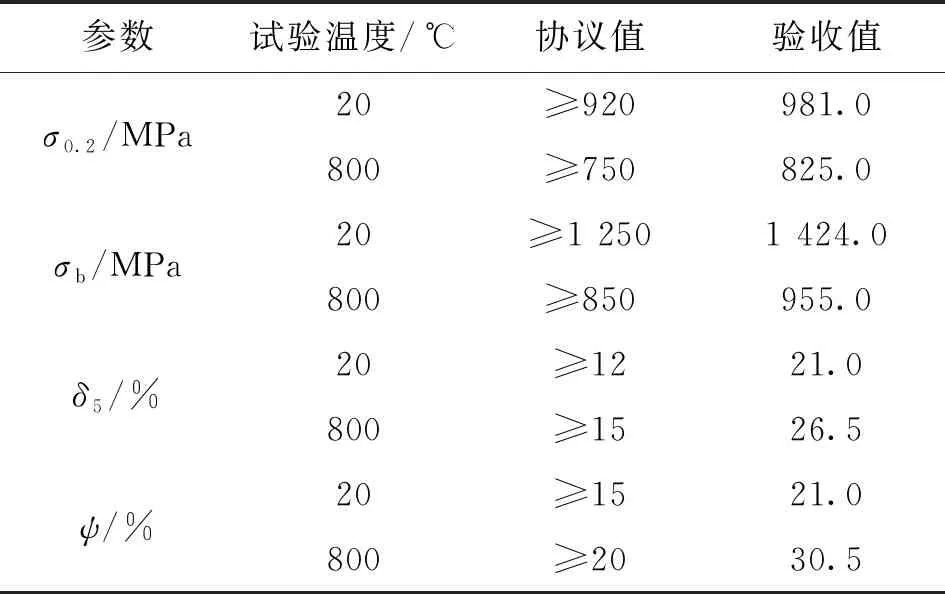
表1 材料GH4586协议值和验收值的力学性能

1.1.2 低周疲劳寿命评估

液体火箭发动机在启动和关机时产生的瞬间热应力是叶片型底前尾缘处产生裂纹的主要原因[14]。低周疲劳寿命是材料承受低周疲劳时达到的失效或断裂循环数[15],本文使用应变寿命法对涡轮进行低周疲劳寿命的预测计算。

应变寿命法[12]基于Manson-coffin公式及其修正公式进行低周疲劳寿命的计算式为

(3)

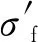
式(3)适用于应力比R=-1,而实际计算过程中,应力比通常不等于-1,故采用Morrow修正模型对其进行修正

(4)

式中σm为平均应力。

1.2 模拟仿真计算方法

1.2.1 流热固耦合数值模拟

本文根据对原涡轮转子叶片的分析提出了叶片顶部加整圈围带的涡轮转子改进模型,并与原始模型计算结果进行对比,最后评估了转子改型前后的高周和低周疲劳寿命。计算数值模拟流程[16]如图1所示,其中振动和强度分析分别使用ANSYS Workbench中的Modal模块、Static Structural模块和Transient Structural模块。

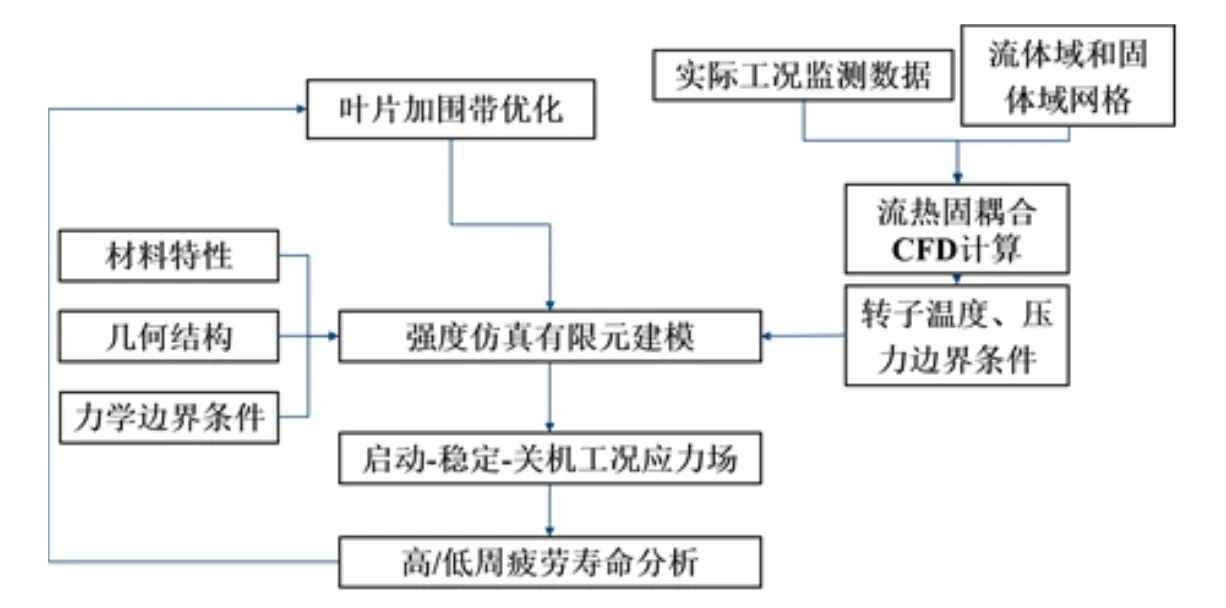
图1 涡轮转子流热固耦合数值模拟流程图

1.2.2 原始模型和改型模型及其边界条件

本文研究的涡轮转子[17]全周共53个叶片,全部为直叶片,对整个涡轮转子建立仿真模型。使用ANSYS对涡轮转子几何模型进行自由模态分析,有限元模型节点数为48万,单元数为31万,自由边界条件不加任何约束。

原始涡轮转子叶片选定材料为GH4586,转子两侧的滚动轴承支承刚度分别为5.89×108、5.45×108N/m,稳态运行工况下转子转速为31 300 r/min。

降低原涡轮转子叶片的叶高1 mm,同时在叶顶处加厚度为1 mm、宽度为13.3 mm的整圈围带,围带外径为176 mm。涡轮转子叶片材料为GH4586,其余工作条件与原始涡轮转子仿真计算条件一致。

1.2.3 启动和停机工况计算点的选取

根据启动阶段燃气温度、入口压力、出口压力及转速随时间的变化曲线如图2所示,叶片温度、压力及转速在短时间内都会发生剧烈变化,其中温度在0.1 s内从300 K增加到1 250 K,剧烈的温度变化会产生很大的热应力[18],需要重点关注。根据启动过程的压力、温度和转速变化,选取了0.09 s、0.35 s、0.50 s、1.07 s、3.00 s这5个典型工况计算时间点对叶片启动工况进行应力计算。

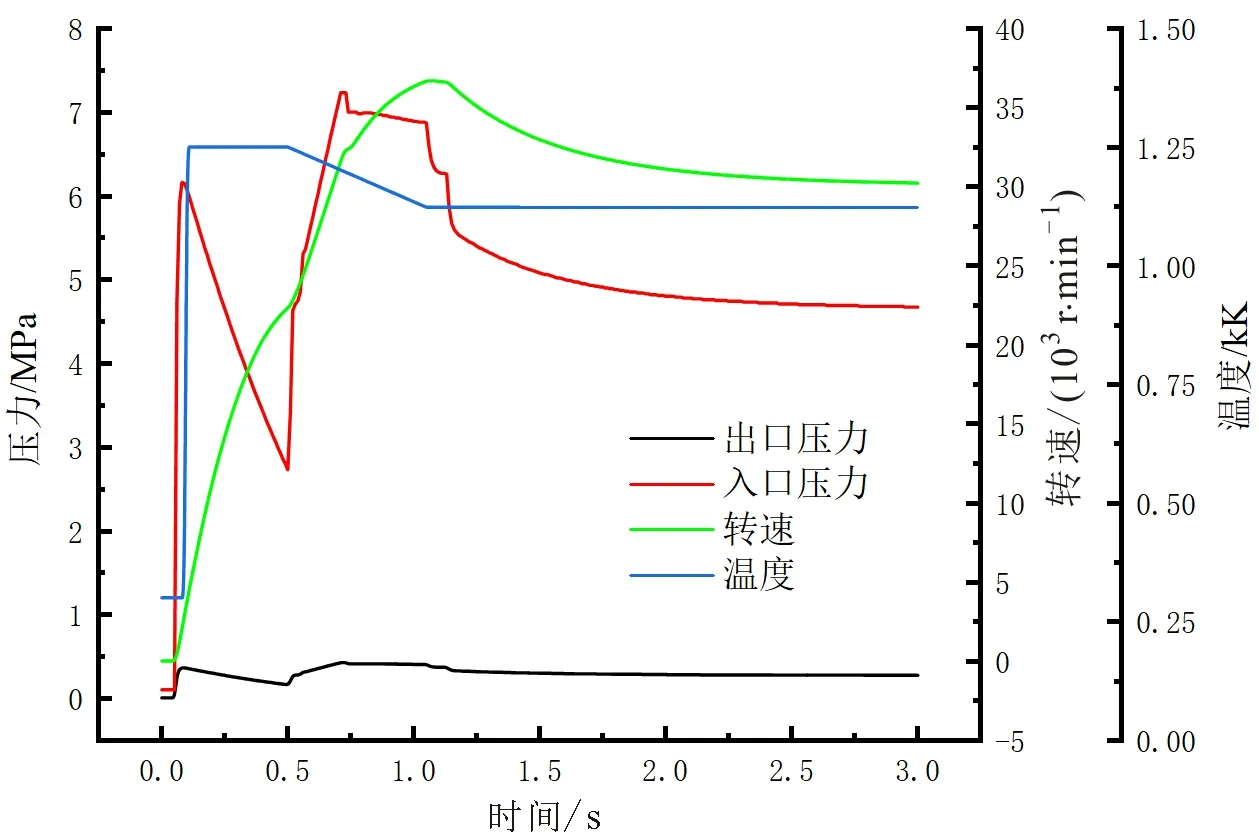
图2 涡轮启动阶段入口参数变化曲线

原涡轮在运行450 s后关机,关机后立即使用氮气进行冷却吹除,氮气温度为288 K,吹除流量为67.20 g/s,吹除压力为0.27 MPa,吹除时间为75 s,使用CFX计算涡轮停机工况起始点(450 s)时的叶片表面流体温度场,流体温度场温度分布较为均匀,温度范围为267～285 K,选取中间温度276 K作为仿真计算时的环境温度。将450 s停机初始时刻点的叶片温度场作为初始温度场,施加相应转速,对涡轮转子进行瞬时热分析计算,选取451 s、452 s、453 s、454 s、455 s这5个计算时间点,计算各个时刻叶片所受综合加载下的等效应力及温度分布[19]。

2 结果与讨论

2.1 原始涡轮转子和叶片加围带改型涡轮转子的振动特性仿真计算

计算涡轮转子叶片自由模态频率(静频)并得到仿真计算结果及振型后[20],进行模态敲击实验,并将所得实验结果与仿真计算结果作对比,结果如表2所示。由表2可以看到,实验所得数据与仿真计算所得结果最大相对误差为3.17%,证明仿真计算结果准确可靠。表3为涡轮转子的动频计算结果和振型。由涡轮盘共振判别准则计算涡轮盘各阶驻波共振转速与工作转速(31 300 r/min)避开率分别为88.8%、112.7%、128.2%,均超过裕度15%,则在稳定运行工况中涡轮盘不会出现驻波共振问题。

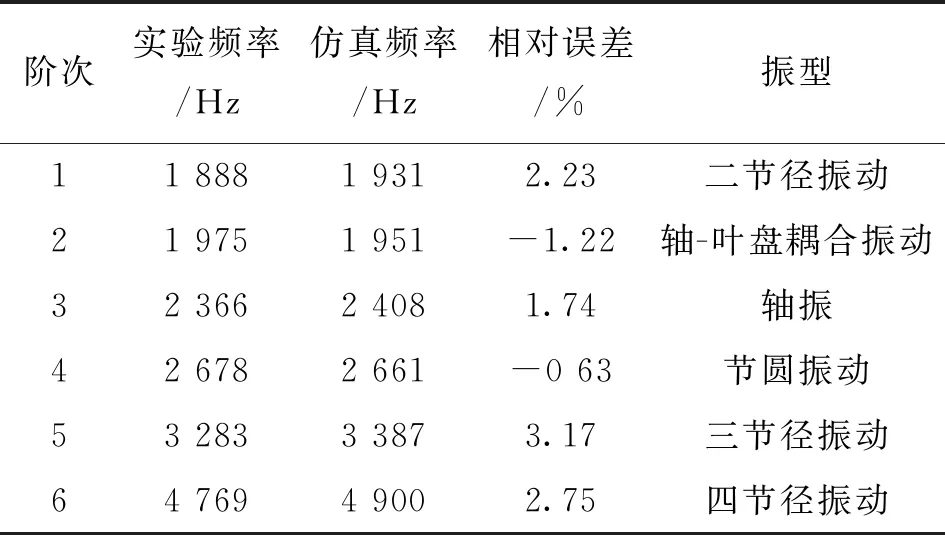
表2 涡轮转子模态静频率实验值与仿真值的对比

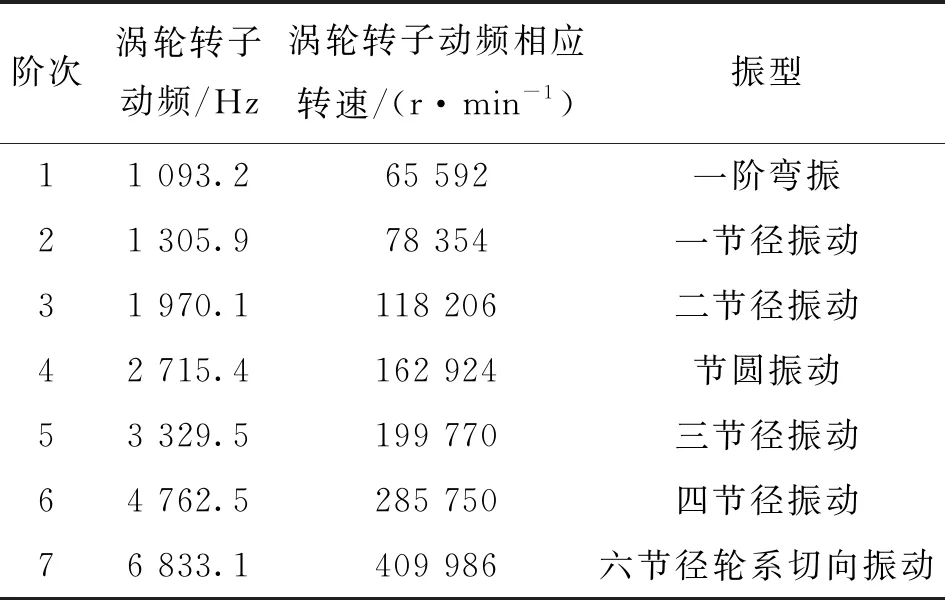
表3 原始涡轮转子仿真计算模态动频率

采用ANSYS Workbench有限元仿真软件中的Modal模块对加围带涡轮转子叶片做仿真计算,得到加围带涡轮转子动频及振型。转子叶片加围带后轮系振动频率和和涡轮盘驻波共振转速避开率均有所上升,轮系振动频率由6 833.1 Hz升高至7 248.2 Hz。各阶动频与涡轮盘驻波共振转速避开率分别为91.2%、128.3%、163.8%,说明加围带涡轮转子同样不会发生叶片共振和轮盘驻波共振问题。加围带涡轮转子振动频率仿真计算结果如表4所示,其中叶片加厚1.0 mm,转速为31 300 r/min。

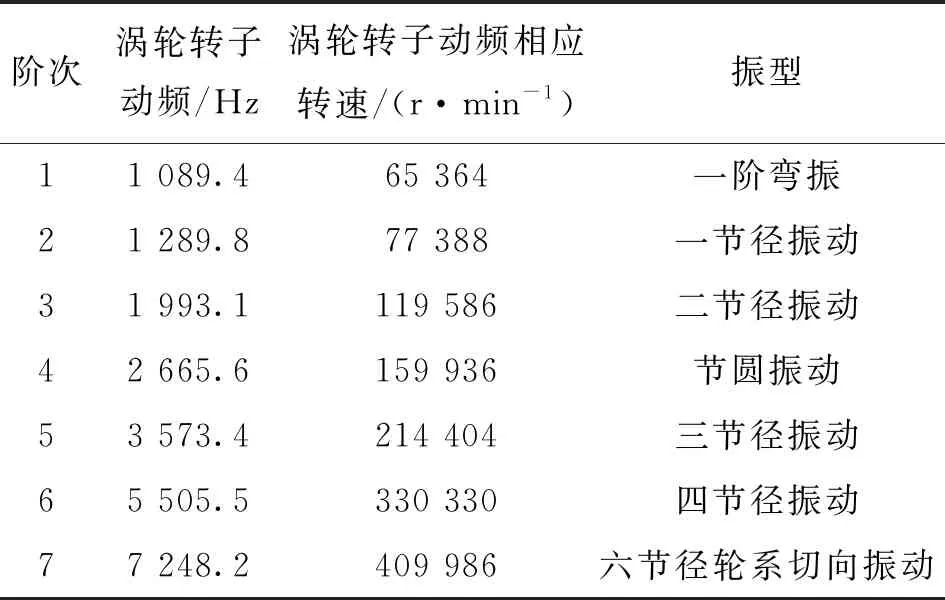
表4 叶片加围带涡轮转子仿真计算模态动频率

2.2 涡轮转子气动特性仿真计算

本文所研究的液体火箭发动机为部分进气[21]结构,部分进气度为0.148,主要结构包括喷嘴、涡轮转子、进气管、排气管等。喷嘴结构为缩放喷嘴,正对着喷嘴出口处的转子叶片数量为7个,全周共53个叶片。

使用ICEM网格划分软件对涡轮叶片流体域和固体域进行结构化网格生成,网格数量分别为856万和472万。流体计算使用k-ε湍流模型,主体计算区域Y+值在20～300范围内,平均值为30,满足计算要求。在喷嘴和排气管部分为非结构化网格,网格数量分别为50、117万,所有壁面均设置边界层,第一层边界层的厚度为0.01 mm。计算网格模型如图3所示。

(a)喷嘴与排气管部分

使用ANSYS-CFX进行气动仿真计算,湍流模型使用k-ε模型,Y+值在全体计算域内满足要求。全周53个叶片中除正对喷嘴出口的7个叶片外其余46个叶片几乎不输出扭矩[22],与部分进气的设计结构一致[23],原始模型稳态工况各动叶片所受扭矩如图4所示。

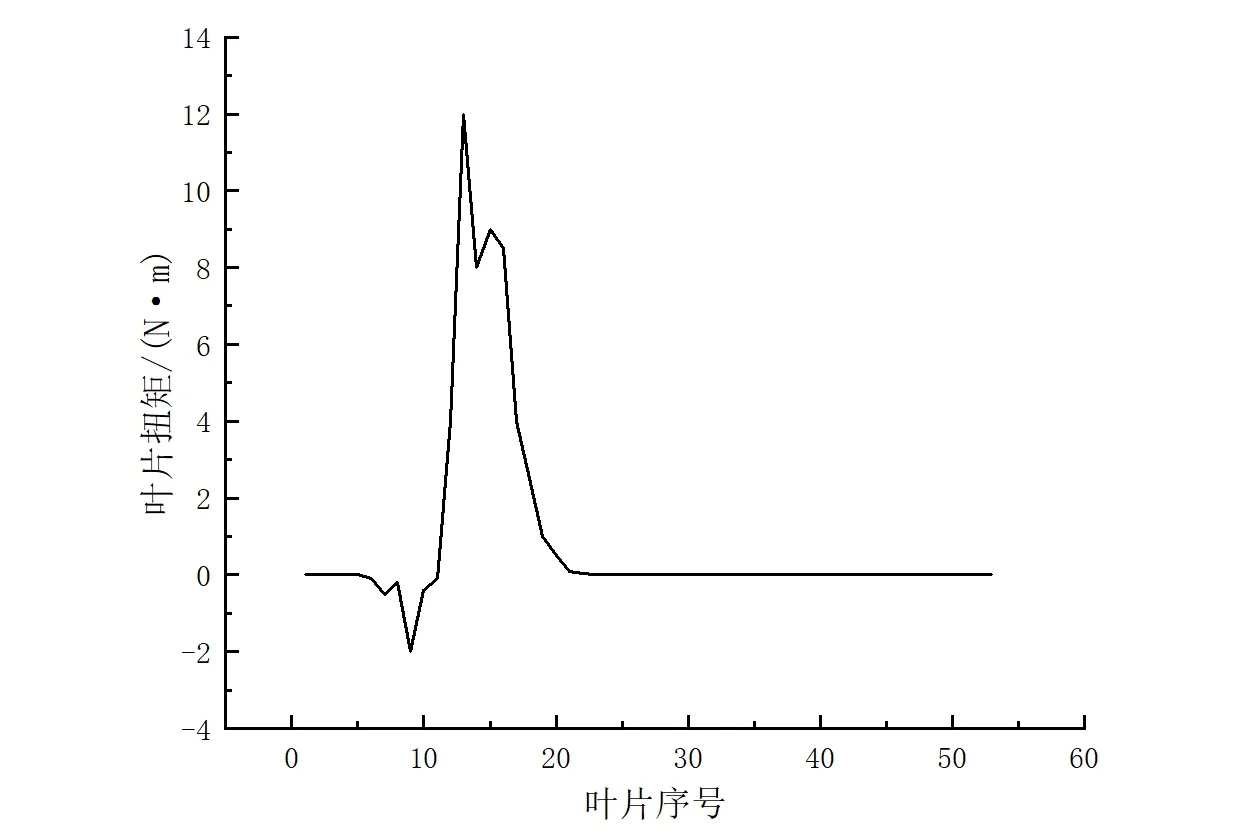
图4 原始模型稳态工况各动叶片所受扭矩

计算得稳态工况的转子功率为203.36 kW,第15号叶片输出扭矩最大值11.83 N·m。在网格无关性验证中,选取983万、1 495万和2 523万3种数量网格进行分析。3种网格计算的为转速31 300 r/min工况下转子功率,1 495万网格计算的功率与2 523万网格计算结果相对误差在0.1%以内。此外,在涡轮转子转速为31 300 r/min时,1 495万网格模型仿真计算功率为203.45 kW,此转速下该涡轮功率设计值为203 kW,与仿真结果相对误差为0.04%,仿真结果可靠。因此本文涡轮转子气动计算仿真网格数量采用1 495万。

2.3 原始涡轮叶片强度特性仿真计算

2.3.1 原始涡轮稳定工况强度仿真计算

对叶片三维几何模型进行网格划分,并对叶片型底倒圆处网格做局部加密。涡轮转子单个叶片网格模型中网格数为6.0万,节点数为9.5万。

原涡轮叶片气动仿真计算中得到的固体域温度场和流体域压力场[24]作为边界条件,将转速设定为31 300 r/min,对转子侧面轴向和周向施加约束,对涡轮转子模型进行强度仿真计算。

考虑包括气动力、热应力和离心力3种力在内的综合加载应力后所得的涡轮转子叶片强度仿真计算结果,如图5所示,可知叶片所受最大应力在型底背弧表面处,最大值为340 MPa,型底前缘圆角应力最大值为280 MPa,均远低于材料疲劳极限值526 MPa。

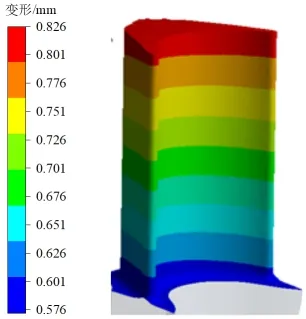
(a)变形

2.3.2 原始涡轮启动工况强度仿真计算

给定转速和前文得到的叶片表面温度场,对涡轮转子进行瞬时热分析仿真计算,结果如表5所示。原始模型启动0.35 s叶片等效应力及温度分布如图6所示,可知涡轮所受等效应力最大值为0.35 s时的954 MPa,位于叶片内弧。

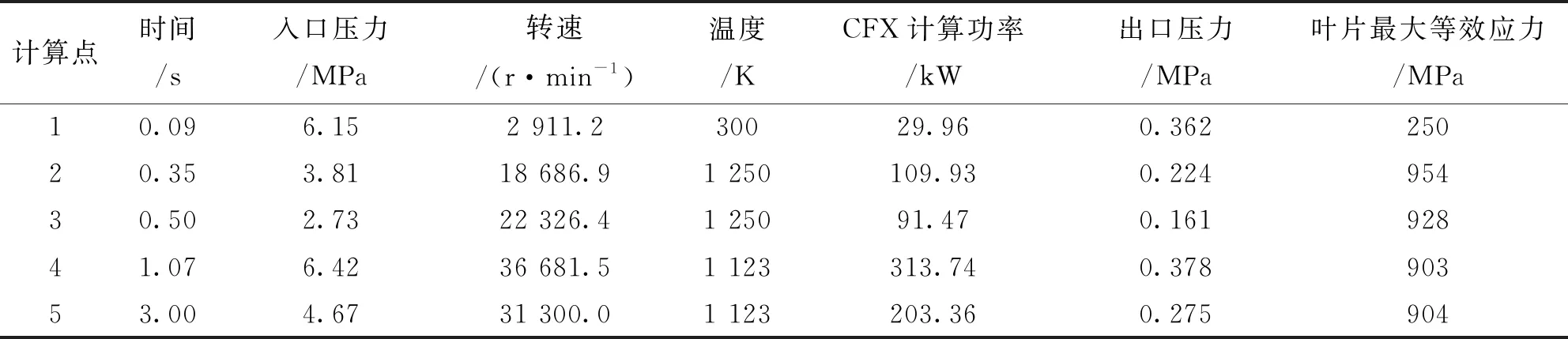
表5 原始涡轮转子模型启动阶段5个计算点叶片应力及转子功率

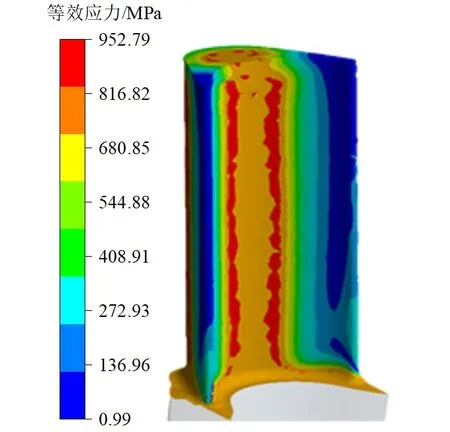
(a)等效应力

2.3.3 原始涡轮停机工况强度仿真计算

原始涡轮转子模型停机工况5个时间点转速及叶片应力如表6所示,原始模型停机455 s叶片等效应力分布及温度分布图7所示,涡轮叶片所受综合加载下的等效应力最大值为455 s时的939 MPa,位于叶片型底前缘,该点的温度为685 ℃。叶片型底前缘所受的等效应力超过了该点材料在此温度下屈服极限值848 MPa。

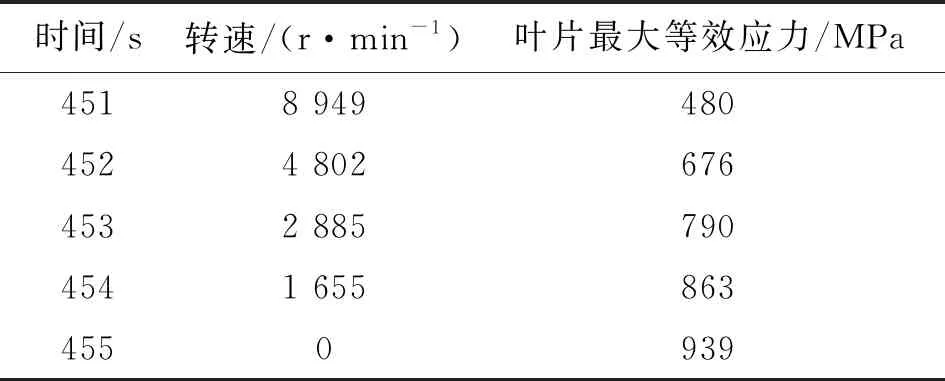
表6 原始涡轮转子模型停机工况5个时间点转速及叶片应力

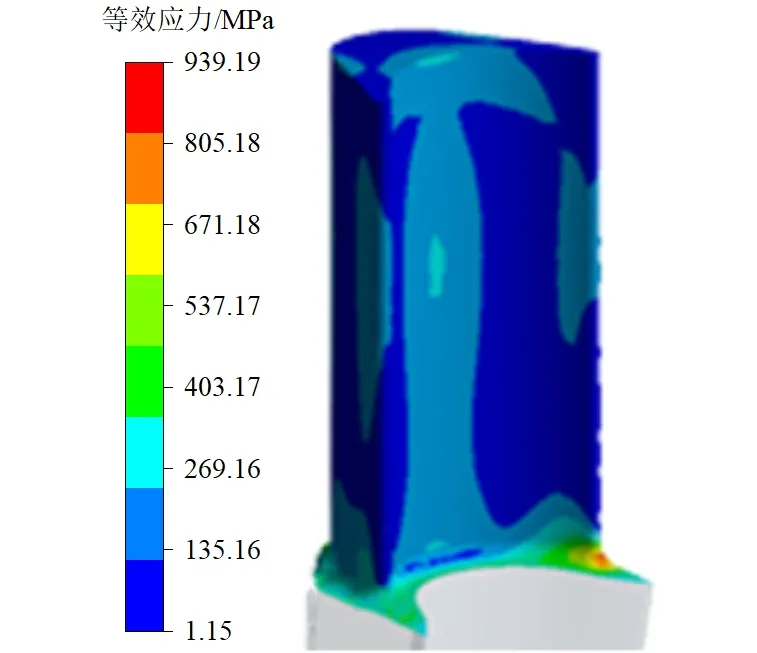
(a)等效应力

2.4 叶片加围带改型涡轮转子强度特性仿真计算

2.4.1 叶片加围带涡轮稳定工况强度仿真计算

采用流热固耦合计算方法对转子进行气动计算,计算区域总网格数为1 593万,通过CFX进行涡轮转子稳态运行工况气动计算,得到转子功率相比于原模型的203.36 kW有所提高,功率为206.70 kW,增幅为1.64%。

在网格无关性验证中,选取997万、1 593万和2 689万3种数量网格进行分析。3种数量网格计算的为转速31 300 r/min工况下转子功率,1 593万网格计算的功率与2 689万网格计算结果相对误差在0.1%以内,因此采用1 593万数量网格对叶片加围带改型涡轮转子进行稳态气动计算。

叶片加围带改型[25]涡轮转子稳态工况叶片应力分布如图8所示,可知叶片加围带模型相比于原叶片模型,在稳定运行工况中所受的最大等效应力从340 MPa下降到了338 MPa,并且两者的位置均为叶片型底背弧处。最大应力点处的温度为921 K,叶片所受最大应力小于该处材料疲劳极限526 MPa,所以叶片加围带涡轮转子模型在稳定运行时不会发生疲劳失效。

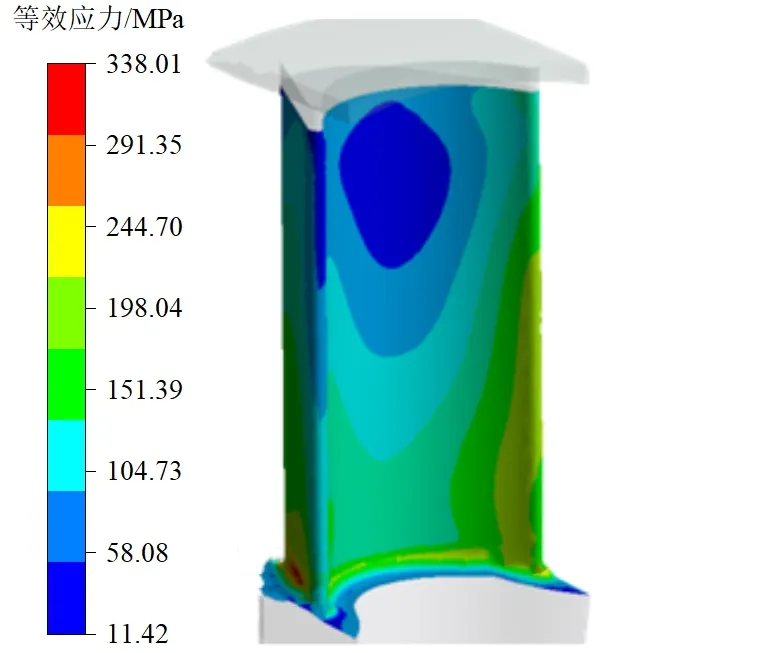
(a)等效应力

2.4.2 叶片加围带涡轮启动工况强度仿真计算

本节中对启动过程的计算方法与第2.3.2节相同,并且选择同样的5个计算时间点,使用ANSYS Workbench的瞬态热分析模块对涡轮转子进行强度仿真计算。改型模型与原始模型启动过程功率及应力对比如表7所示,改型模型启动过程0.35 s叶片等效应力及温度分布图9所示。叶片加围带模型所受最大应力为928 MPa,时间点与原模型一致为启动后0.35 s,相较于原模型的956 MPa,下降了2.73%。

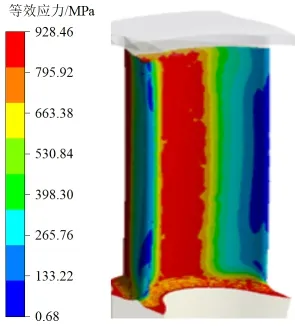
(a)等效应力

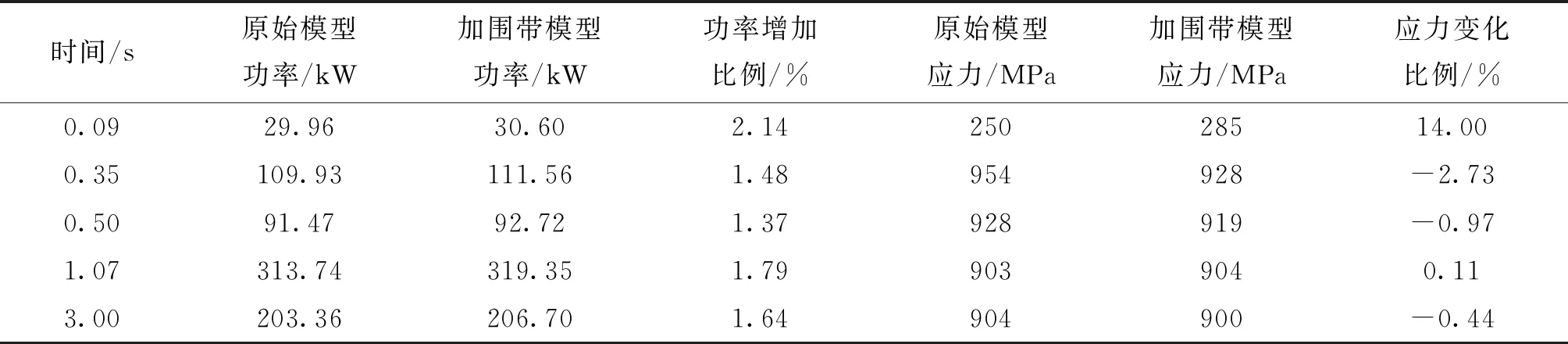
表7 改型模型与原始模型启动过程功率及应力对比

2.4.3 叶片加围带涡轮停机工况强度仿真计算

本节所有设置与第2.3.3节相同,450 s初始温度场为稳态运行工况温度场,使用ANSYS Workbench的瞬态热分析模块对叶片加围带涡轮转子停机过程进行强度计算,选取同样的5个计算时间点,并将所得结果与原始模型的相对比,改型模型与原始模型停机过程应力对比如表8所示,改型模型停机过程455 s叶片等效应力分布及温度分布如图10所示。叶片加围带涡轮转子模型在停机过程中所受最大应力的时间点与原始模型一致,均为455 s,应力值由原模型的939 MPa下降为935 MPa,下降幅度为0.53%。

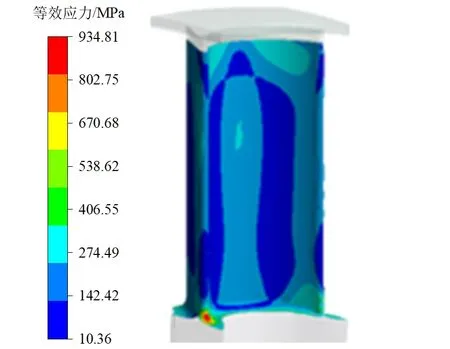
(a)等效应力

2.5 叶片启动工况高低周疲劳寿命评估

2.5.1 原始模型启动工况高低周疲劳寿命评估

本文选取了涡轮在启动过程中0.30 s、 0.35 s和1.07 s这3个可能发生高周疲劳失效的时间点,采用式(1)(2)进行高周疲劳计算。表9为分别采用材料验收性能参数值和协议性能参数值下涡轮叶片3个计算时间点处的高周疲劳安全系数。启动后时间点0.30 s处采用协议值的材料特性计算的高周疲劳安全系数为1.03,采用验收值的材料特性计算的为1.23,两者均小于按照NASA标准安全系数1.4的要求。

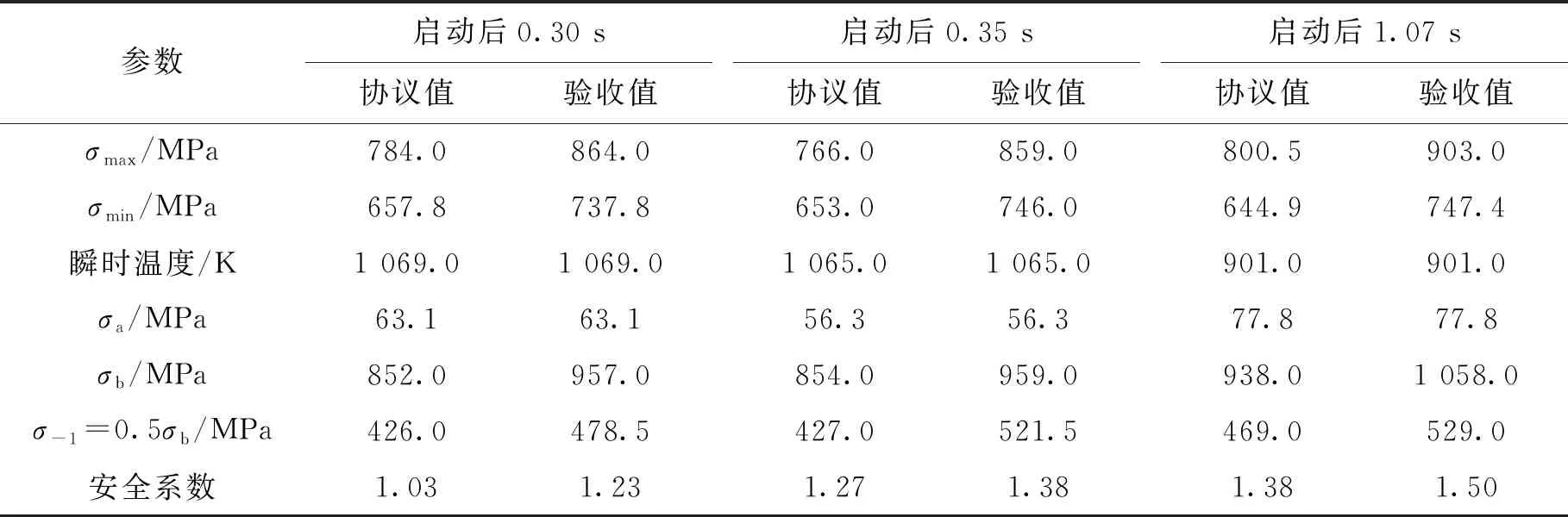
表9 原始模型启动过程高周疲劳安全系数计算

图11为仿真计算得到的涡轮转子叶片在启动-稳定运行-停机全过程中叶片型底的最大应变,涡轮转子型底最大的应变为启动后0.35 s时的1.793%。将所得的最大应变1.793%乘以1.25低周疲劳分析系数后,代入材料GH4586修正过的Manson-coffin公式,得Nf=92。取安全系数为4[17]时,涡轮转子叶片的低周疲劳寿命为23,说明该涡轮转子可以安全启动-稳定-停机过程23次。

图11 原始叶片型底最大应变

2.5.2 改型模型启动工况高低周疲劳寿命评估

使用与第2.5.1节相同的计算方法,分别采用验收性能系数和协议性能系数对0.30 s加围带涡轮转子叶片的高周疲劳安全系数进行计算,并与原始模型的安全系数进行对比。

改型模型启动工况0.30 s高周疲劳安全系数计算如表10所示,可知采用材料验收值时,叶片加围带模型产生裂纹处最大应力为828 MPa,相较于原始模型的864 MPa,下降了36 MPa;采用材料协议值时,叶片加围带模型产生裂纹处最大应力为743 MPa,相较于原模型的784 MPa,下降了41 MPa。动态气动应力从原模型的63 MPa下降到了加围带模型的60 MPa。同时,加围带模型在0.30 s时分别采用材料验收系数参数和材料协议值时的高周疲劳安全系数为1.59、1.42,相对于原模型的1.23、1.03有大幅提升,满足安全系数大于1.4的要求。

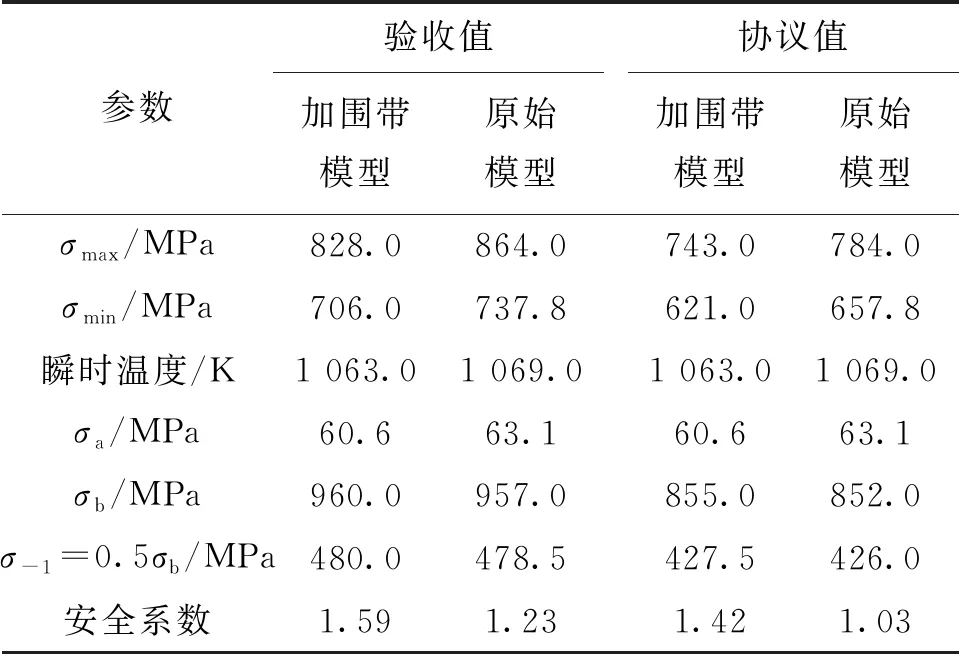
表10 改型模型启动工况0.30 s高周疲劳安全系数计算

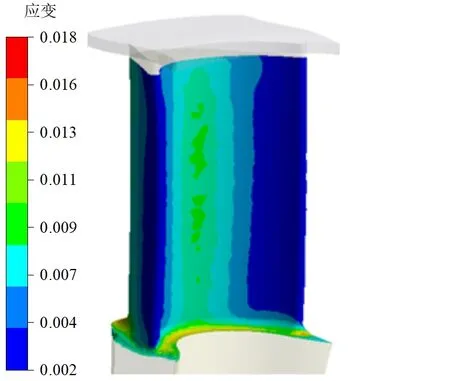
图12 改型模型启动后0.35 s叶片开裂处最大应变

将该应变乘1.25低周疲劳分析系数后,代入Morrow模型修正的Manson-Coffin公式,得到Nf=90,取安全系数为4时,该叶片低周疲劳寿命次数为22,即可以安全运行整个过程22次,相较于原模型的23次,降低了1次,仍满足使用要求。叶片加围带改型方案在11所在的地面试验得到验证,此发动机为CZ4改型,已安全飞行多次,遥测返回数据验证了该涡轮能保证安全运行。

3 结 论

本文使用ANSYS的流热固耦合计算方法对原涡轮转子模型和叶片加围带涡轮转子改进模型进行了振动、气动和强度仿真计算。对原始模型进行强度计算时考虑了启停工况各关键时间点的流动、传热、瞬态温度场、转速的影响,分别计算了稳态运行工况、启动和停机过程3个过程模型所受综合加载下的等效应力,找到了叶片所受最大应力的部位。为降低叶片所受气动冲击应力,提出了叶片加围带涡轮转子模型。最后分别计算了优化前后的涡轮在启停过程中的高周疲劳安全系数和低周疲劳寿命。计算分析得到如下结论。

(1)原涡轮转子叶片的六节径轮系切向振动频率为6 833.1 Hz,加围带涡轮叶片六节径轮系切向频率上升至7 248.2 Hz,二者均与气流激励频率相差较远,转子叶片不会发生共振现象;涡轮盘各阶驻波共振转速避开率均超过裕度15%,也不会发生轮盘驻波共振。

(2)稳态综合加载时,叶片加围带涡轮转子模型叶片所受最大等效应力为338 MPa,较原模型的340 MPa下降了2 MPa,最大等效应力的位置是叶片的型底背弧处,该位置运行温度下的疲劳极限为526 MPa,明显大于叶片所受最大等效应力;启动后0.35 s叶片加围带涡轮转子模型叶片等效应力最大值相比于原涡轮转子模型从954 MPa降低到928 MPa,降幅为2.73%;叶片加围带涡轮转子模型在停机过程中所受最大等效应力的时间点与原模型一致,均为停机瞬间,应力值由原模型的939 MPa下降为935 MPa,降幅为0.53%。

(3)叶片加围带模型在启动工况0.30 s时采用协议值的材料特性计算的高周疲劳安全系数为1.42,采用验收值的材料特性计算的高周安全系数为1.59,比原始模型启动后0.30 s的安全系数1.03、1.23有着大幅提高,且均大于安全系数1.4的要求;叶片加装围带后,载荷略有增加,叶片加围带模型型底最大应变为启动后0.35 s时前缘底部的1.803%,相比原模型的1.793%增加了0.56%,得到涡轮转子叶片低周疲劳循环次数为22次,与原始模型相比降低了1次,仍满足要求,改型后发动机已安全飞行数次。