射弹高速入水尾拍载荷和弹道特性的数值研究
2022-08-17王晓辉孙士明
王晓辉,李 鹏,孙士明,张 珂
(中国船舶科学研究中心 水动力学国家重点实验室,江苏 无锡 214082)
0 引 言
超空泡射弹的高速入水过程,是其由空中弹道进入水中弹道的一个重要的过渡环节。自弹体接触自由液面瞬间,到形成超空泡水下航行状态,由于涉及流动介质突变引起的入水冲击,以及入水空泡发展、包覆状态改变引起的水动力变化,射弹的入水载荷形式较为复杂。
在射弹高速入水载荷研究方面,苏轶龙[1]在考虑水的可压缩性基础上,对射弹垂直入水过程进行了数值研究,研究表明,基于不同的载荷形成机理,射弹垂直入水载荷先后表现为入水冲击载荷与入水水动力载荷特征。进而,陈晨等[2]、孟庆昌等[3]对射弹垂直入水后超空泡航行状态的水动力进行了数值模拟研究,并获得了与Serebryakov等[4]、易文俊等[5]试验研究相一致的结果。
射弹扰动运动状态下高速入水,通常还会伴随射弹的尾拍及水动力载荷的变化。Hrubes[6]通过超空泡射弹水下发射试验,对射弹超空泡状态下的尾拍弹道稳定机理进行了研究。孟庆昌等[7]、赵成功等[8-9]对射弹水下超空泡航行状态的尾拍特性及射弹结构参数、初始扰动的影响进行了一定的研究。
基于射弹入水、水中弹道的相关性,本文重点对伴随尾拍的射弹垂直入水过程开展数值模拟研究,以获得射弹的尾拍水动力载荷、尾拍弹道运动特性,并在尾拍对射弹水弹道的影响分析基础上,对其水弹道性能进行评估。
1 数值计算方法及验证
1.1 入水的耦合欧拉—拉格朗日求解方法
有限元的显式动态求解方法是由模拟高速冲击等高速动力学问题发展而来,特别适用于瞬时的,包含接触、碰撞行为的非线性动力学问题的模拟。通过引入描述水动力学行为的状态方程,并结合可用于自由液面捕捉的CEL(coupled Eulerian-Lagrangian analysis)分析技术,使得射弹高速入水过程也能够通过显式动力学方法进行求解。
本文基于CEL 方法的入水数值模拟,采用接触算法捕捉入水空泡的形态演化。空气域采用不考虑质量、强度的真空材料(void material)加以模拟;水介质采用Hugoniot 形式的米埃—格林爱森(Mie-Grüneisen)状态方程描述其体积响应,采用牛顿黏性剪切模型描述其黏性剪切响应。
Hugoniot形式的Mie-Grüneisen状态方程表述为

牛顿黏性剪切模型为

式中,S为应力偏量,ė为应变率偏量,γ̇= 2ė为工程偏应变率,μ为动力黏度。
本文射弹高速入水问题中,水介质线性Us-UpMie-Grüneisen 状态方程的基本参数为:密度ρ0=9.832×102kg/m3,c0= 1.4506×103m/s,s= 0,Γ0= 0,μ= 1×10-3Pa·s.
1.2 射弹的垂直入水模拟及方法验证
本文采用文献[6]中超空泡射弹外形开展射弹垂直入水的数值研究,其几何模型如图1所示,空化器直径d=1.42 mm,射弹长度l=157.4 mm,射弹尾端直径D=13.12 mm。

图1 射弹几何模型Fig.1 Geometric model of projectile
基于以上数值求解模型,射弹以970 m/s 垂直入水过程中入水空泡的形态演化如图2所示。
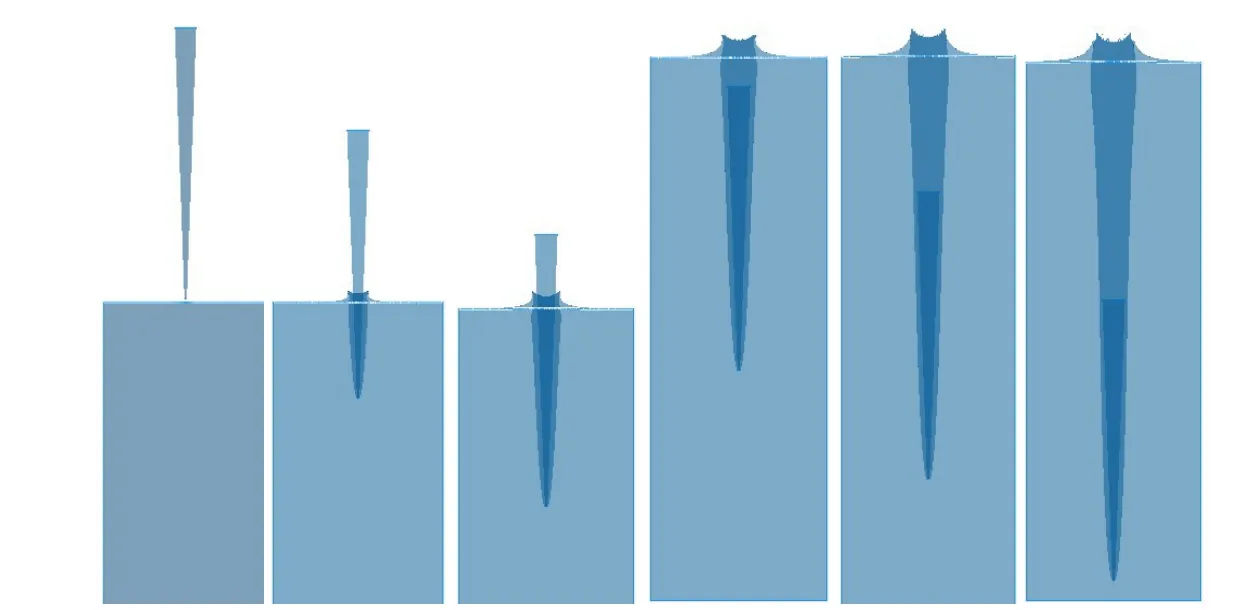
图2 射弹垂直入水过程Fig.2 Vertical water-entry process of projectile
可见,经射弹头部撞水、入水空泡敞开,逐步形成包覆于弹体的入水超空泡,射弹随即进入水中航行状态。将CEL 方法获得的射弹入水后水中航行超空泡形态,与文献[6]中试验及Logvinovich 独立膨胀原理[10]获得的超空泡形态(泡内压力取水的饱和蒸汽压)对比,如图3~4所示。
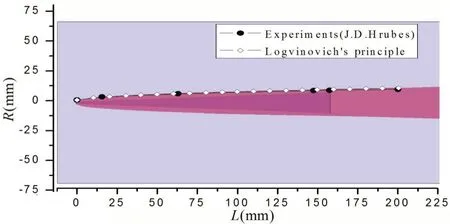
图3 射弹水中航行超空泡形态与试验、理论模型结果对比Fig.3 Comparison of cavity shapes among computation,experiment and theory
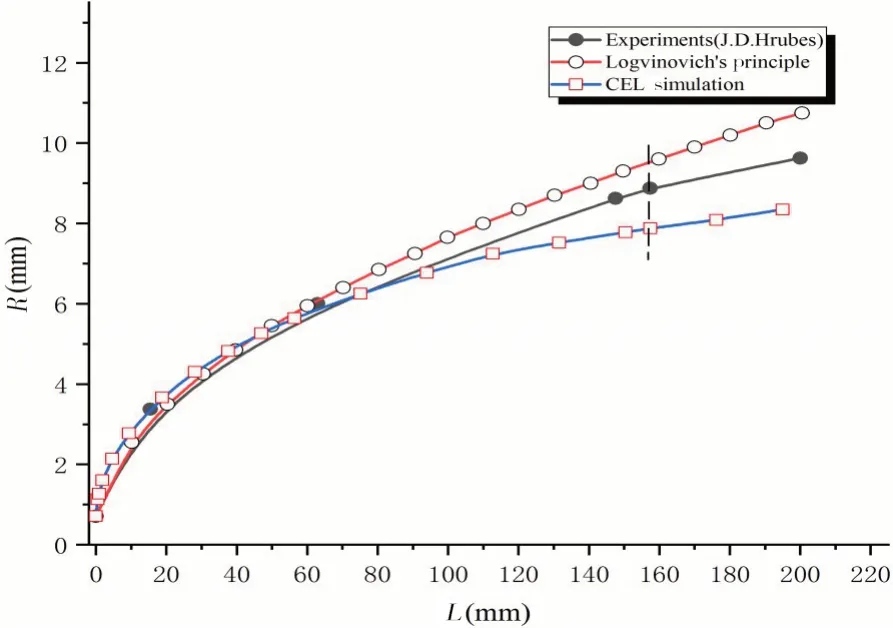
图4 数值模拟的超空泡轮廓与试验、理论模型结果对比Fig.4 Comparison of cavity profiles among computation,experiment and theory
可见,沿空泡长度方向,数值模拟与试验数据、理论计算结果在空泡前段吻合较好:以空化器直径d为特征尺寸,空泡轮廓在纵向尺度近似L/d=50 的范围内,CEL 数值模拟、独立膨胀原理均与试验结果相接近。空泡长度方向尺度继续增加,空泡半径尺寸误差累积,差异逐渐明显。以射弹尾端处空泡截面半径为例,相对于试验光测数据,CEL数值模拟结果略小,而独立膨胀原理计算结果略大,相对误差分别为11.2%、7.34%。
在理想垂直入水状态下,射弹高速入水载荷形式较为简单:弹体在触水瞬间受到轴向入水冲击载荷作用,而后入水空泡敞开,水的惯性流动形成后受到连续的入水水动力载荷作用,如图5所示。

图5 射弹垂直入水载荷曲线Fig.5 Time history of axial load in the projectile’s vertical water-entry process
由一维弹性碰撞理论,刚性平板冲击可压缩水面冲击压力的极限值的估算公式为

式中,ρ为水的密度,c为水中声速,v0为结构入水速度。CEL 数值模拟获得的入水冲击载荷峰值Fmax= 2000 N,小于由此极限压力峰值计算的冲击载荷(2223 N)是合理的,两者的相对误差为10%。
基于细长体理论并考虑水体的可压缩性,圆盘空化器超空泡航行阻力系数Cd的计算方法[4]为
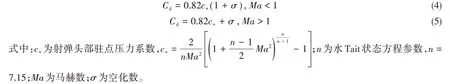
以射弹头部半径为特征尺寸,由以上理论公式计算得到射弹水下超空泡航行的阻力系数Cd=0.89,而CEL数值计算得到的平均阻力系数为0.9715,与理论结果的相对误差为9.16%。
综上可见,显式动力学CEL方法在高速入水空泡界面捕捉、入水载荷计算方面具备一定的求解精度,将其应用于超空泡射弹高速入水的研究是可行的。
2 射弹垂直入水尾拍的数值模拟
作为射弹高速入水典型特征的入水超空泡,同时构成了射弹入水、水中运动的动力学边界。由于发射初始扰动、射弹空中弹道扰动因素的存在,射弹入水过程中不可避免地会存在一定的攻角、侧滑角散布。射弹在扰动运动状态下,带攻角、侧滑角入水,弹体与入水空泡壁面接触进而形成了射弹的尾拍(tail-slap)现象。
基于上文数值求解模型,开展射弹在1000 m/s速度、1°攻角(假设其为空中段飞行最大攻角)垂直入水过程的数值模拟,获得射弹入水的首次尾拍过程如图6所示。可见,伴随射弹尾拍,入水空泡表现出显著的不连续演化特征。

图6 射弹带攻角垂直入水过程Fig.6 Water-entry process of projectile with attack angle
射弹在入水的首次尾拍后,弹体反向偏转,再次触水、尾拍,进而形成射弹伴随尾拍的、水下超空泡航行状态。射弹姿态偏转及后续的尾拍过程如图7所示。

图7 射弹后续的尾拍过程Fig.7 Subsequent tail-slap process of projectile
3 射弹尾拍的载荷及弹道特性
3.1 射弹尾拍的载荷及弹道特性
以上文射弹在1000 m/s速度、1°攻角垂直入水过程为例,其在伴随尾拍的入水及水下超空泡航行过程中,弹体受到的轴向载荷Fx、侧向载荷Fz变化分别如图8~9所示。
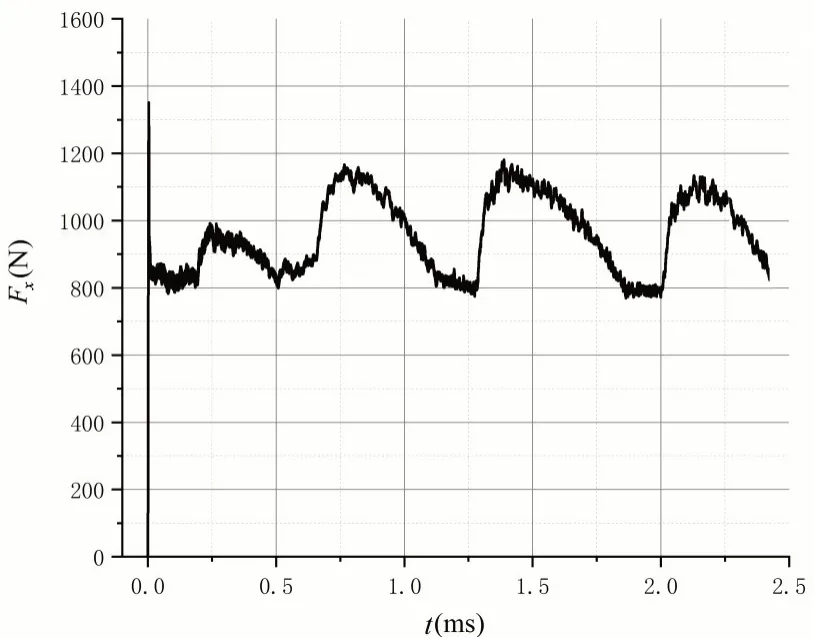
图8 射弹尾拍引起的轴向载荷变化Fig.8 Change of axial load caused by projectile’s tail-slap
与图7 相对应,可以看到射弹在完成入水后形成数次尾拍。随着射弹尾拍触水,弹体的轴向载荷、侧向载荷迅速增加;而后随着尾拍作用下射弹姿态的恢复,弹体的轴向、侧向载荷也随之下降。射弹单次尾拍的载荷变化历程表现出显著的非对称特征。
在射弹伴随尾拍的入水、水下航行过程中,弹体姿态偏转角速度的变化如图10所示。

图10 射弹伴随尾拍航行过程中偏转角速度变化Fig.10 Change of angular velocity caused by projectile’s tail-slap
可见,射弹尾拍起始、结束时刻均伴随有射弹角速度曲线斜率的突变,使射弹的角速度变化明显地分为射弹尾拍作用阶段与超空泡完整包覆航行阶段。在射弹的尾拍作用阶段,弹体的姿态偏转由尾拍侧向载荷主导;在超空泡完整包覆航行阶段,攻角航行状态下作用于射弹头部的侧向载荷分量对其姿态偏转产生影响;不同的载荷量值决定了不同阶段的角速度变化的斜率。射弹的往复尾拍运动使射弹的角速度也呈现往复的、近似周期性的变化特征。
值得注意的是,与图8、图9中单次尾拍引起的弹体载荷的非对称特征相对应,弹体尾拍过程在进入水体与反向偏转回到空泡中的角加速度是有差别的。在图10中选取射弹角速度变化的一个周期,以特征点A-G加以表征。其角速度变化过程大致可分为3 个阶段:(1)从A-B或D-E,射弹尾段以一定的角速度穿越空泡界面,开始在水中滑行,并在B、E达到最大的滑行浸没角,此阶段角速度逐步减小直至为零;(2)从B-C或E-F,射弹尾段由水中滑行状态向空泡内侧反向偏转,并在C、F离开空泡壁面,此阶段反向偏转角速度逐步增大,在尾拍结束时刻C、F达到最大;(3)在C-D或F-G,射弹处于超空泡完整包覆航行状态,可近似认为射弹在空泡内以恒定角速度偏转。
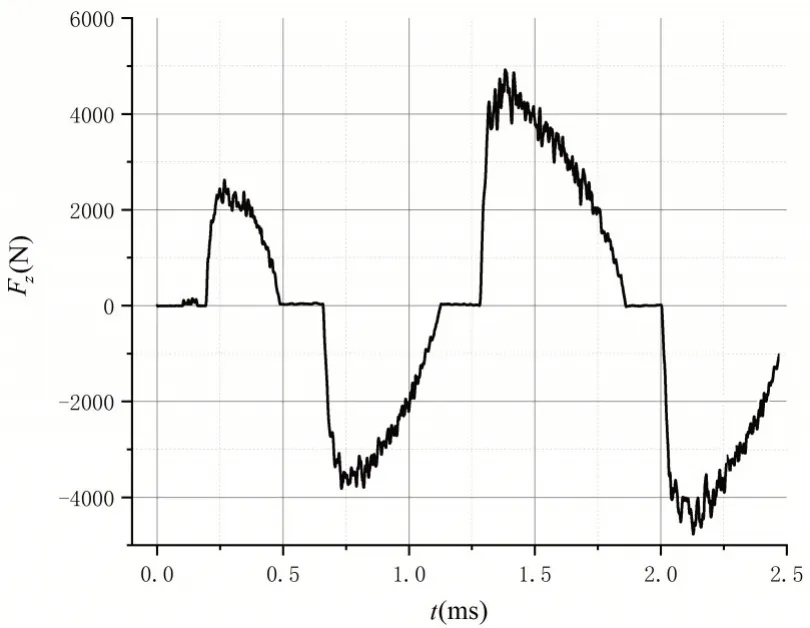
图9 射弹尾拍引起的侧向载荷变化Fig.9 Change of lateral load caused by projectile’s tail-slap
由于角速度的存在,射弹尾拍过程中(A-C或D-F)的有效攻角αeff为

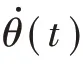
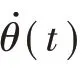
相应地,伴随射弹带攻角入水、超空泡状态下的往复尾拍,射弹的航行攻角α的变化如图11所示。
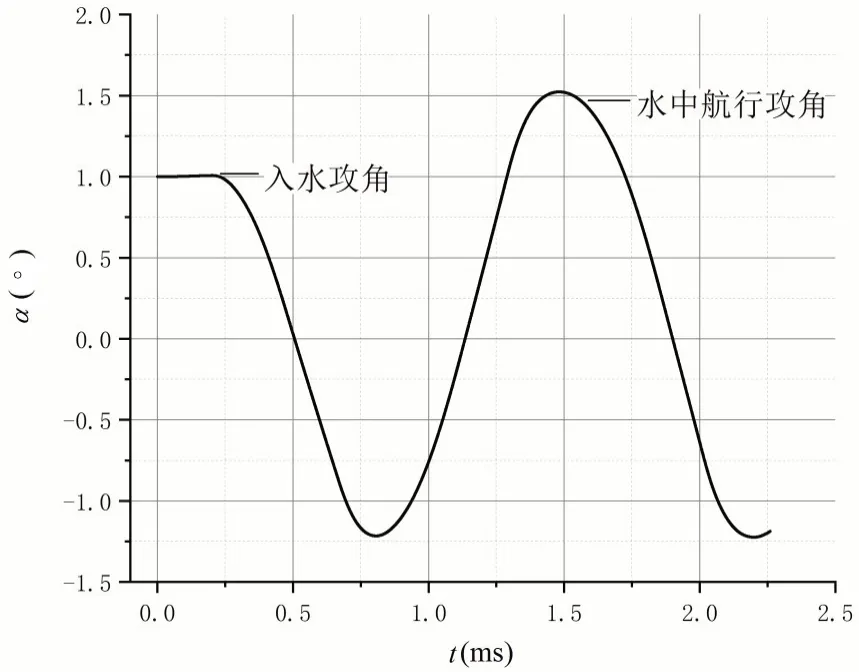
图11 射弹尾拍引起的航行攻角变化Fig.11 Change of attack angle caused by projectile’s tail-slap
3.2 射弹尾拍对水弹道性能的影响
就射弹入水的首次尾拍而言,由于介质突变,射弹在入水尾拍形成的侧向水动力载荷,作为初始扰动力,是形成射弹超空泡航行往复尾拍运动的主要原因。初始扰动作用的大小,在射弹入水首次尾拍的空泡演化特征上也有所体现。
以射弹1000 m/s 入水速度下,不同攻角垂直入水过程为例(为使射弹尾拍触水位置在弹体质心后,本文入水攻角控制在2°以内),数值模拟得到其首次尾拍过程中的弹体姿态偏转及空泡形态演化,如图12 所示。可见,射弹的入水攻角越大,入水初始扰动越大,射弹尾拍的作用行程更长,尾拍引起的空泡不连续演化特征也越显著。

图12 不同攻角下射弹垂直入水过程对比Fig.12 Comparison of projectile’s water-entry processes at different attack angles
值得注意的是,由于射弹与入水空泡壁面之间存在一定的间隙,本文研究的射弹在以较小攻角、侧滑角入水过程中(如图12(a)射弹以攻角α= 0.5°入水),弹体姿态的微幅偏转始终在入水空泡形成的空间范围以内,射弹并未发生尾拍现象。在此入水、水下航行状态下,射弹通过作用于头部空化器的侧向力恢复弹体姿态偏转,其航行阻力也与理想的垂直入水状态相近。
对于射弹在完成入水、进入水下超空泡航行状态下的尾拍,以射弹入水速度1000 m/s,入水攻角α分别为0.75°、1.25°、1.75°下的垂直入水过程为例,其在伴随尾拍的入水及水下超空泡航行过程中,轴向载荷Fx、侧向载荷Fz变化的对比,分别如图13~14所示。

图13 不同攻角下射弹垂直入水轴向载荷变化对比Fig.13 Comparison of axial loads in projectile’s waterentry process at different attack angles

图14 不同攻角下射弹垂直入水侧向载荷变化对比Fig.14 Comparison of lateral loads in projectile’s waterentry process at different attack angles
可见,在射弹入水初期,连续的2次尾拍引起的弹体轴向、侧向载荷变化有明显差别;在射弹第3、4 次尾拍,其水动力载荷的形式、幅值,及尾拍作用时间相接近,表明射弹开始进入稳定的水下超空泡尾拍航行状态。针对射弹尾拍对其水中弹道性能的影响,本文基于以此阶段射弹的尾拍载荷予以研究。
同时,在本文研究的入水攻角2°以内,射弹在不同攻角下,水下稳定尾拍航行过程的水动力载荷的幅值和尾拍作用时间相近。以下取射弹入水速度1000 m/s,入水攻角为1.25°的入水状态,对其第4次尾拍及空泡完整包覆状态航行过程中的航行阻力变化取均值,对射弹水下超空泡尾拍航行状态的弹道性能进行评估,如图15所示。

图15 射弹尾拍航行阻力与无尾拍航行阻力对比Fig.15 Comparison of drag forces with and without projectile’s tail-slap
射弹尾拍航行阻力均值以F′表示,不考虑尾拍时射弹的航行阻力以F表示,定义尾拍阻力增加系数k=F′/F=Cd′/Cd。其水下超空泡尾拍航行状态下k= 1.22,航行阻力增加了近22%。可见,由于尾拍的存在,射弹的航行阻力的增加是十分显著的。
3.3 射弹水弹道性能的评估
不考虑重力作用,射弹在水下运动可简化为

对上式积分,并令速度衰减系数b=CdπR2ρ/2m,可以得到

再次积分得到弹体水中运动位移s与时间t的关系:

进而可得到其速度衰减与位移的关系为

将射弹水下超空泡尾拍航行状态,以考虑尾拍阻力增加系数k的方式向理想的超空泡航行状态等效,得到射弹在水中超空泡理想航行状态与尾拍航行状态下,弹体速度随射程的衰减,如图16所示。
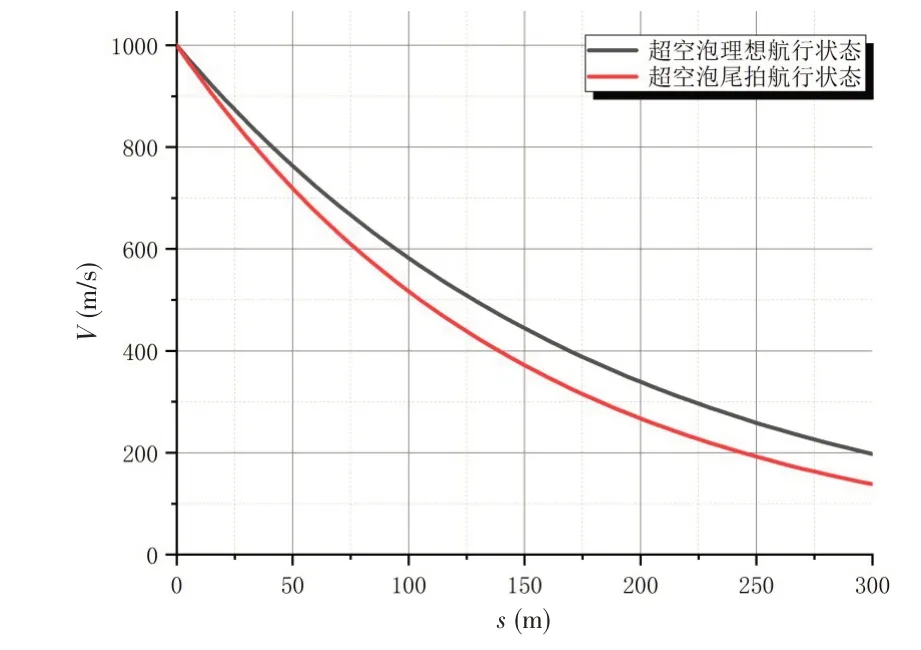
图16 射弹水下超空泡航行速度衰减随位移的变化Fig.16 Variation of projectile’s velocity attenuation with penetration distance
随着射弹入水深度的增加和入水速度的衰减,其空泡尺度不断减小。从射弹的水下毁伤效能角度,要求在其水弹道末段保持一定的航速;而从弹道稳定角度,则要求其保持超空泡水下航行状态不变,即空泡仍可以将弹体完整包覆。超空泡射弹水下射程的估计,即在这两方面约束下加以开展。
在弹道稳定性方面,取射弹长度不超过空泡最大直径位置对应长度作为空泡完整包覆约束,则射弹在空化数σ=0.0065达到此临界要求,其航行空泡包覆状态如图17所示。

图17 射弹水下航行空泡包覆临界状态Fig.17 Critical cavity profile of projectile in underwater motion
在射弹的垂直入水状态下,考虑水下环境压力随射弹入水深度的变化、弹体速度的衰减,将以上射弹的弹道规律转化为空化数随射程的变化,如图18所示。

图18 射弹垂直入水空化数随射程的变化Fig.18 Variation of cavitation number with penetration distance in projectile’s vertical waterentry process
结合图16可以看到,超空泡射弹垂直入水时,随着入水深度的增加,其有效射程主要受到空泡包覆的完整性和弹道稳定性制约;而在其最大射程内,射弹的末段毁伤速度仍有一定裕量,即超空泡射弹应用于较浅的水深,可将此裕量转化为更大的射程。
以最大作战深度20 m 为例,以此最大深度的环境压力估算,并考虑弹体速度的衰减,可得到空化数随射程的变化,如图19 所示。可见,超空泡射弹在1000 m/s 初速下,20 m 作战深度范围内,其水下有效射程可达近200 m,射弹尾拍对其射程的影响也非常显著。而提高射弹的发射初速,还可进一步增加其水下射程。
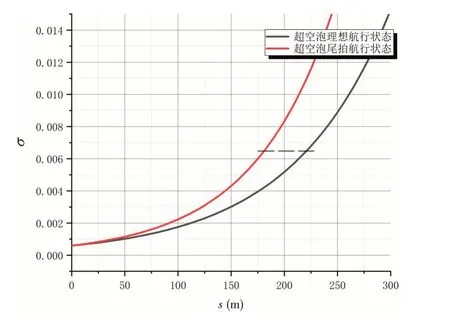
图19 射弹20m水深超空泡航行空化数随射程的变化Fig.19 Variation of cavitation number with penetration distance in projectile’s underwater motion with a depth of 20 m
4 结 语
本文针对射弹高速入水问题,采用显式动力学CEL 方法开展了射弹入水尾拍的相关数值模拟研究,捕捉到了射弹尾拍伴随的空泡壁面的不连续演化特征,并对其尾拍水动力载荷、尾拍弹道运动特性进行了研究。
在尾拍对射弹水弹道的影响方面,对射弹单个尾拍周期内航行阻力取均值,通过引入尾拍阻力增加系数的方式,将其尾拍航行状态向理想的超空泡航行状态等效,获得了射弹水下超空泡尾拍航行过程的弹道性能。进一步对射弹水下射程的评估表明,采用超空泡射弹武器进行舰艇的水下近程防御是可行的。
