非常规内倾船型骑浪数值预报方法研究

储纪龙，鲁 江，顾 民

（中国船舶科学研究中心 水动力学重点实验室，江苏 无锡 214082）

0 引 言

国际海事组织（IMO）于2020年12月发布了第二代完整稳性衡准临时指南[1]，目前，正在制定第二代完整稳性衡准直接评估方法解释性文件。二代完整稳性衡准改变以往只依靠经验公式制定衡准的方法，涵盖了五种波浪稳性失效模式：参数横摇、纯稳性丧失、瘫船稳性、过度加速度和骑浪/横甩，其中骑浪/横甩涉及波浪中船舶操纵性、耐波性、快速性和波浪稳性等多学科的交叉耦合，是一种强非线性的复杂稳性失效模式。由于骑浪/横甩现象的复杂性和直接稳性评估的高难度，目前急需一种准确有效的骑浪/横甩数值预报方法。所谓骑浪，就是船舶在随浪或尾斜浪中高速航行时，被波浪捕获并以波速前进的现象。通常船舶在波浪的下坡段发生骑浪，处于骑浪状态下的船舶，多数会因航向不稳定性而不可控制地转向，发生横甩，横甩产生的离心力严重时可以导致船舶倾覆。

第二代完整稳性衡准中每种失效模式衡准都由三个层次的评估方法组成，分别为第一层薄弱性衡准、第二层薄弱性衡准和直接稳性评估，三层评估方法的计算复杂性依次递增，评估的准确性也依次提高。最新提案[1]中给出了骑浪/横甩直接稳性评估的相关要求：对于骑浪/横甩失效模式，船舶运动数值模拟至少包括纵荡、横荡、横摇和首摇四自由度运动，不考虑的自由度运动应该满足静平衡假定；船舶运动数值模拟应该考虑由于船体漩涡脱落而产生的水动力，除了静水操纵力，还应包括因波浪粒子速度和船舶速度共存而产生的水动升力；采用合适的舵控制方法；初始航速应该设置得足够小以避免假骑浪（artificial surf-riding）的发生。

针对骑浪/横甩数值预报方法的研究，国外学者Umeda 等[2]采用考虑线性波浪力的纵荡-横荡-横摇-首摇四自由度MMG 模型定性预报了ITTC A2 渔船的骑浪/横甩现象；Hashimoto 等[3]拓展已有的纵荡-横荡-横摇-首摇四自由度MMG 模型预报了内倾船的骑浪/横甩现象；Matsubara 等[4]基于纵荡-横荡-横摇-首摇四自由度MMG模型，结合临界波法和直接计数法计算了短峰不规则波中船舶由横甩导致大角度横倾的概率；Angelou 等[5]基于六自由度数学模型数值模拟风帆游艇的骑浪/横甩现象，获得了风帆游艇的动态稳定性图谱和稳性失效的临界波陡；Carrica 等[6-7]应用CFD 方法再现了船舶在规则波和不规则波中横甩的发生过程。国内对于骑浪/横甩数值模拟方法的研究相对较少，于立伟等[8-9]采用操纵性与耐波性耦合的六自由度弱非线性统一模型，对一艘渔船随浪条件下的骑浪/横甩运动进行数值模拟，探究渔船的骑浪/横甩界限，并改进舵出水模型，分析舵出水对横甩运动的影响；张宝吉等[10]以四自由度操纵性方程为基础，数值模拟了渔船在随浪、尾斜浪下骑浪/横甩现象，分析了不同波浪条件下渔船的运动规律。

国内对于骑浪/横甩的研究主要集中于渔船的骑浪/横甩现象数值预报，而对于内倾船这样具有双桨双舵、细长体、穿浪船艏、水线以上舷侧内倾、大型上层建筑等特性的典型非常规高速船的骑浪/横甩数值模拟几乎没有。因此，本文针对非常规内倾船型，建立考虑波浪中双桨双舵实时出入水变化的纵荡-横荡-横摇-首摇四自由度运动耦合的数学模型，采用FORTRAN 语言编写计算程序，进行运动仿真，预报非常规内倾船的骑浪现象，可为骑浪/横甩直接稳性评估奠定基础。

1 数学模型

1.1 船舶运动坐标系

本文采用两种坐标系，如图1 所示：空间固定坐标系O-ξηζ，原点O位于水平面，起始于波谷，ζ轴向下为正，用来描述波浪；船体坐标系G-xyz，以船舶重心G为原点，x轴在中线面内，平行于基面，指向船首为正，z轴向下为正。图中χ为航向角，φ为横摇角，δ为舵角，ξG为船舶重心G在空间固定坐标系中与原点处初始波谷的纵向相对位置。

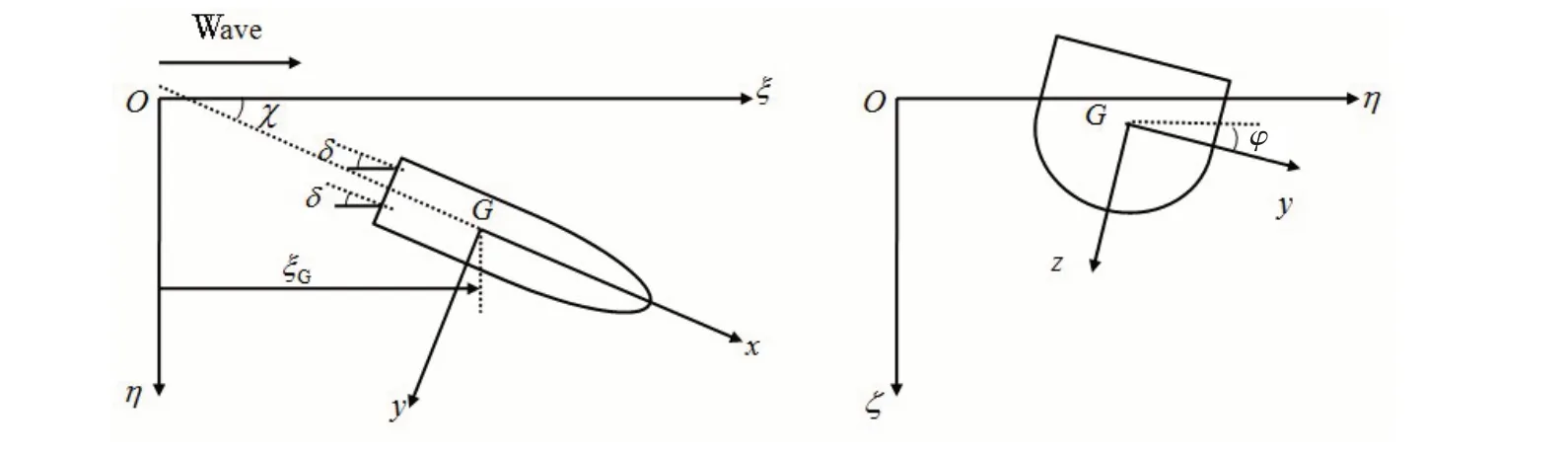
图1 坐标系Fig.1 Coordinate systems

1.2 数学模型构建

船舶发生骑浪/横甩时船舶遭遇频率远小于升沉和纵摇的固有频率，升沉和纵摇运动可通过静平衡法求解稳定平衡点来近似[11]。本文基于MMG 模型构建纵荡-横荡-首摇-横摇四自由度数学模型进行骑浪运动数值预报，该数学模型满足IMO 提案中对骑浪/横甩直接稳性评估的相关要求[1]。数学模型如下所示：

1.3 船体力

船体力XH,YH,NH和KH的表达式为

1.4 静水阻力

静水阻力R(u)的表达式为

式中，ρ为水密度，SF为船舶湿表面积，CT为船舶总阻力系数，L为船舶垂线间长，g为重力加速度。

1.5 螺旋桨推力和舵力

IMO 提案中对骑浪/横甩直接稳性评估的相关要求指出，骑浪/横甩数值模拟方法应该正确地模拟由于船体漩涡脱落而产生的水动力，也就是除了静水操纵力，还应包括因波浪粒子速度和船舶速度共存产生的水动升力。因此，本文在双桨双舵的螺旋桨推力模型和舵力模型里考虑波浪粒子速度的影响，同时还进一步考虑了螺旋桨和舵实时出入水的影响。

双螺旋桨推进时，左右两侧螺旋桨受波浪粒子速度和实时出入水情况的影响，产生的推力不同，同时还会产生首摇力矩，这里左舷推力用TP表示，右舷推力用TS表示，首摇力矩用NP表示。双螺旋桨推力XP和首摇力矩NP的表达式如下：

式中：nP为螺旋桨转速；DP为螺旋桨直径；tP为螺旋桨推力减额分数；KT为螺旋桨推力系数；JPP、JPS分别为左右侧螺旋桨的进速系数；wp为螺旋桨伴流分数；yPP、yPS分别为左右侧螺旋桨横向位置；uWPP、uWPS分别为左右侧螺旋桨处波浪粒子速度；β0P、β0S分别为左右侧螺旋桨有效推力系数，这里设定为β0P=APP/AP0,β0S=APS/AP0，AP0为螺旋桨面积，APP,APS分别为左右侧螺旋桨实时浸水面积。

与螺旋桨一样，左右两侧舵受波浪粒子速度和实时出入水情况的影响，产生的舵力不同，同时还会产生首摇力矩，舵力模型在参考文献[12]提供的舵力模型基础上修改考虑波浪粒子速度和实时出入水的影响，各方向舵力的表达式如下：

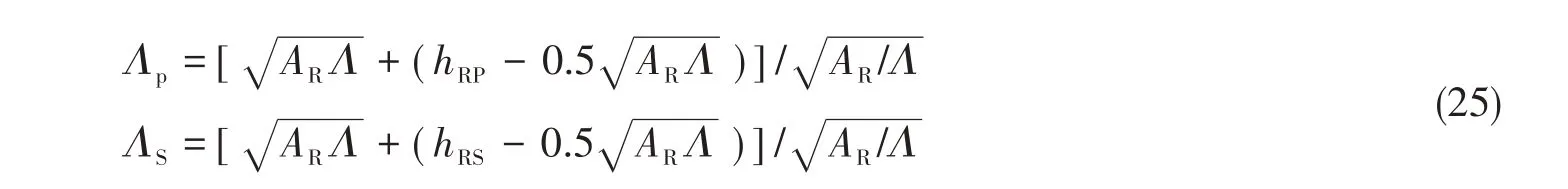
式中：tR为舵阻力减额系数；xR为舵的纵向位置；zR为舵的垂向位置；aH为操舵诱导船体横向力的修正因子；xHR为操舵诱导船体横向力作用点纵向位置；zHR为操舵诱导船体横向力作用点垂向位置；yRP、yRS分别为左右舵的横向位置；ARP、ARS分别为左右舵实时浸水面积；URP、URS分别为左右舵来流速度；αRP、αRS分别为左右舵攻角；fαP、fαS分别为左右舵力系数；ΛP、ΛS分别为左右舵实时展弦比；ε为桨舵伴流分数比；η为螺旋桨直径与舵展比；κ为桨舵相互作用系数；uWPP、uWPS分别为左右舵位置处的波浪粒子速度；AR为舵面积；Λ为舵展弦比；hRP、hRS分别为左右舵相对于波面的瞬时垂向高度。

1.6 波浪力

波浪力主要包括Froude-Krylov 力和绕射力，其中纵荡波浪力的绕射效应通过IMO 提案SDC 2/INF.10附件35[13]中日本提出的经验修正因子μx进行修正。各方向波浪力的计算公式如下所示：

1.7 非线性横摇阻尼

横摇阻尼是预报横摇运动的关键，尤其大幅横摇运动，船舶横甩时通常伴有大幅横摇，甚至倾覆，本文研究中采用了线性和立方项阻尼系数，公式如下：

式中，α和γ分别为线性项和立方项阻尼系数。

2 模型介绍

本文选取ONR 内倾船开展骑浪数值模拟研究。ONR 内倾船是典型的非常规高速船，具有细长体、穿浪船艏、水线以上舷侧内倾，以及双桨双舵等特性。由于舷侧内倾，ONR内倾船的横摇恢复力矩小于舷侧垂直或外飘的相似船型，因此该船在恶劣海况中高速航行时容易发生稳性失效。ONR 内倾船的主要参数和横剖面图分别如表1和图2所示。

表1 船型主要参数Tab.1 Main parameters of the ship

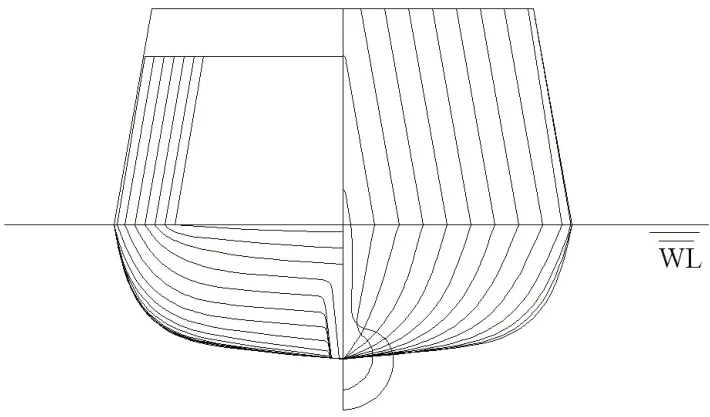
图2 船体横剖面图Fig.2 Body plan of the ship

3 结果与分析

基于以上建立的骑浪/横甩数学模型，分别分析舵和螺旋桨出水、纵荡绕射效应和非线性水动力导数对内倾船骑浪运动的影响。试验结果来自参考文献[3]。

3.1 舵和螺旋桨出水

计算工况如下：波长与船长比λ/LPP为1.25；波陡H/LPP为0.05；航向为5°、15°、22.5°、30°和37.5°；Fn从0.25 到0.5，间隔为0.01。分别计算不考虑舵和螺旋桨出水和考虑舵和螺旋桨出水两种情况，数值计算的内倾船周期运动区域和骑浪运动区域划分如图3和图4中的左图所示，计算获得的骑浪边界与试验结果对比如图3和图4中的右图所示。

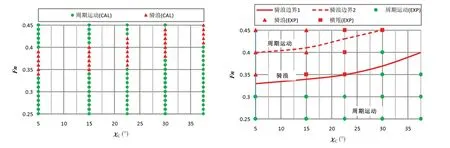
图3 船舶运动模式数值计算结果与试验结果[3]对比（不考虑舵和螺旋桨出水）Fig.3 Comparison of boundaries of ship motion modes between numerical results and experimental results without rudders and propellers emersion

图4 船舶运动模式数值计算结果与试验结果[3]对比（考虑舵和螺旋桨出水）Fig.4 Comparison of boundaries of ship motion modes between numerical results and experimental results with rudders and propellers emersion

从图3 和图4 中可以看出，不考虑舵和螺旋桨出水时，固定航向下内倾船随着Fn的增大，船舶运动从周期运动过渡到骑浪运动再到周期运动，而考虑舵和螺旋桨出水后计算的骑浪区域扩大；同时考虑舵和螺旋桨出水时，随着航向的增大，内倾船发生骑浪的临界弗劳德数Fncr增大。通过与试验结果对比可以看出，除了试验中横甩情况，考虑舵和螺旋桨出水计算的周期运动和骑浪运动区域与试验结果更为一致。而试验中内倾船发生横甩的情况，数值计算中只发生了骑浪，通常骑浪被看作是发生横甩的先兆，而横甩是骑浪平衡的危险分岔，数值计算中内倾船发生骑浪后达到稳定，舵和螺旋桨出水等非线性因素产生的扰动没有打破内倾船的骑浪平衡，还需要进一步研究。同时横甩运动与船舶初始状态息息相关，数值计算中未设置初始扰动，而试验中无法排除初始扰动。

选取的航向为5°时，不考虑舵和螺旋桨出水时纵荡速度u的时间历程曲线如图5所示。当内倾船的Fn为0.25 时，内倾船做稳定的周期运动，稳定状态的纵荡速度u呈规则的正余弦。随着航速增大，内倾船发生骑浪，如图5中Fn为0.35的情况，内倾船的航速增大到波速，稳定状态的纵荡速度u不变。当航速继续增大时，内倾船很快加速到大于波速，做稳定的周期运动，如图中Fn为0.45 的情况所示，稳定状态的纵荡速度u呈规则的正余弦。

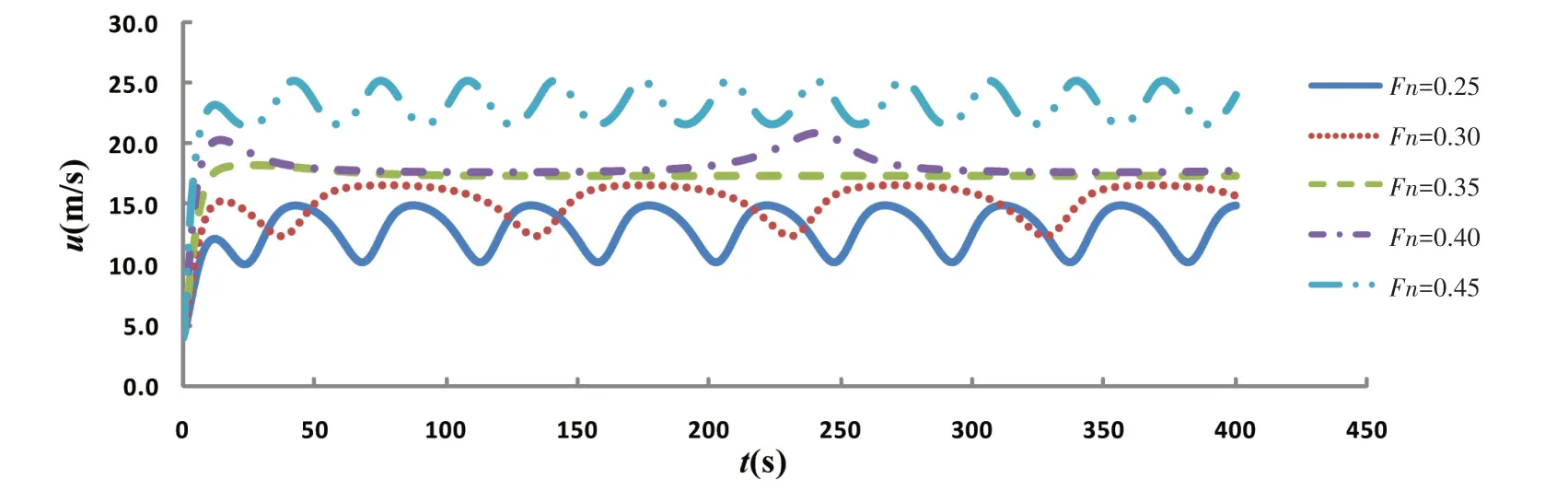
图5 纵荡速度u时间历程（不考虑舵和螺旋桨出水）Fig.5 Time histories of u without rudders and propellers emersion

图6 为航向为5°时考虑舵和螺旋桨出水后内倾船的纵荡速度u的时间历程曲线。考虑舵和螺旋桨出水后，内倾船发生骑浪的Fn范围增大。以Fn为0.45 的工况为例，考虑舵和螺旋桨出水后，螺旋桨推力效率降低，舵效降低，在纵荡波浪力的作用下，内倾船被加速到波速发生骑浪。图7 为该工况下内倾船左右舵实时浸水面积ARP、ARS和螺旋桨有效推力系数β0P、β0S的时间历程曲线，从图中可以看出内倾船发生骑浪后，左右舵的浸水面积ARP、ARS由原来的24 m2分别降到7.8 m2和8.3 m2，左右螺旋桨有效推力系数β0P、β0S由1.0分别降到0.66和0.69，舵和螺旋桨效率均降低很多。

图6 纵荡速度u时间历程（考虑舵和螺旋桨出水）Fig.6 Time histories of u with rudders and propellers emersion

图7 骑浪运动舵和螺旋桨出水动态时间历程Fig.7 Time histories of rudders and propellers emersion of surf-riding motion

3.2 纵荡绕射影响

分析波浪绕射效应对船舶运动模式的影响，由于切片法无法计算纵荡方向的波浪绕射力，这里纵荡绕射效应采用经验公式（32）对纵荡Froude-Krylov力进行修正。分别计算考虑纵荡方向的绕射效应和不考虑纵荡方向的绕射效应两种情况，获得的内倾船周期运动和骑浪运动区域的边界如图8所示。

图8 考虑纵荡绕射和不考虑纵荡绕射计算的船舶运动模式边界对比Fig.8 Boundaries of ship motion modes with and without surge diffraction

从图中可以看出，考虑纵荡绕射效应计算结果与试验值吻合得更好。因为纵荡方向波浪力只考虑Froude-Krylov 力时，波浪力估算值偏大，使得内倾船提前达到骑浪平衡状态。而且航向角为5°时，不考虑纵荡绕射效应所计算的骑浪边界对应的Fn小于0.3，与骑浪横甩第一层薄弱性衡准Fn≤0.3 不易发生骑浪横甩的结论不一致。因此，纵荡方向的绕射效应对船舶骑浪横甩运动影响较大，直接数值模拟时不可忽略。

3.3 非线性水动力导数

分析非线性水动力导数X'vv、X'vr、X'rr、Y 'vvv、Y 'vvr、Y 'vrr、Y 'rrr、N'vvv、N'vvr、N'vrr、N'rrr对船舶运动的影响，分别计算考虑非线性水动力导数和不考虑非线性水动力导数两种情况下内倾船运动模式，计算结果如图9 所示，获得的骑浪运动和周期运动的边界重合，说明非线性水动力导数对内倾船骑浪运动预报影响较小，在缺乏试验数据时可忽略。

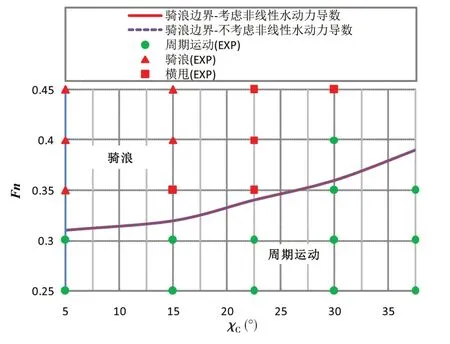
图9 考虑非线性水动力导数和不考虑非线性水动力导数计算的船舶运动模式边界对比Fig.9 Boundaries of ship motion modes with and without nonlinear hydrodynamic derivatives

4 结 论

本文以双桨双舵的ONR 内倾船为例，开展了非常规船型的骑浪数值预报方法研究，得出了以下结论：

（1）本文构建的四自由度纵荡-横荡-首摇-横摇运动数学模型，可以预报随浪和尾斜浪中双桨双舵非常规内倾船的骑浪运动，用于骑浪直接稳性评估。

（2）舵和螺旋桨出入水是影响非常规内倾船骑浪运动的一个关键因素，进行数值预报时不可忽略。

（3）纵荡方向的绕射效应对非常规内倾船骑浪运动影响较大，进行数值预报时不能忽略。

（4）非线性水动力导数对非常规内倾船骑浪运动预报影响较小，在缺乏试验数据时可忽略。

该力学模型需要进一步考虑横甩的潜在影响因素，如大幅横摇对双桨双舵出水的影响等，为双桨双舵船型的横甩直接评估提供可靠力学模型。