基于样本船的兴波阻力智能预报方法

陈 帅，周广利，王 超，蒋彩霞

（1.中国船舶科学研究中心，江苏 无锡 214082；2.哈尔滨工程大学 船舶工程学院，哈尔滨 150001）

0 引 言

为了提高船型优化设计系统的计算效率，近似模型的引入至关重要。目前以减小兴波阻力性能为优化目标的船型设计问题较多，而船体曲面变形技术和兴波阻力预报技术为近似模型训练提供样本数据，随着计算机和人工智能技术的迅速发展，构建基于样本船型的兴波阻力高精度近似计算模型来解决优化过程中的海量计算具有重要研究意义。

船体曲面变形技术需要解决的是如何以较少的设计变量对船体曲面进行变换，本文根据自主开发的NURBS技术[1]，采用改进平移法和自由变形技术对船体曲面进行修改生成海量的船型样本方案。船体兴波阻力快速预报可以通过求解定常兴波问题得到，在上两个世纪中，出现了一些经典的兴波势流理论，如Michell 理论、Kelvin 源（或Havelock 源）、Neumann-Kelvin（NK）理论和新细长体理论等，这些理论为后续的兴波问题研究奠定了基础。Dawson[2]在自由面和船体表面布置Rankine 源来求解定常兴波问题，使得Rankine 源法在船舶兴波阻力预报上取得了巨大的成功。本文开发了基于贴体网格[3]的Dawson方法计算程序，只需数十秒就可以计算一次兴波，适用于样本船型预报。

在近似模型方面，冯佰威[4-5]综述了近似技术在船型自动优化中的意义并进行应用；万德成等[6]讨论了近似模型在船型优化中的应用现状以及研宄难点；刘志强[7]以OPTShip-SJTU[12]求解器为基础，分析了不同近似模型的计算精度；Huang[8]提出了一种基于径向基函数的近似模型降低了货船优化的计算成本；Vesting[9]采用近似模型与局部搜索方法相结合大幅度提高了船用螺旋桨的设计效率；Priftis[10]采用近似模型研究了不确定条件下船舶的参数化设计和多目标优化问题，在设计初期对总阻力、运费率和成本进行优化；Kim[11]采用响应面Kriging模型优化Series-60船型，结果表明响应面法大大降低计算成本。为了实现兴波阻力的智能预报，本文分别对样本船型生成、兴波阻力预报和近似模型构建展开研究，首先提出曲面变形技术的理论方法，以ITM 和FFD 两种方法对船体变形进行应用。其次，给出兴波理论和数值计算方法，验证本文兴波阻力计算程序的可靠性。最后，建立基于SLE-BP 神经网络的兴波阻力预报近似模型，利用KCS船型进行智能预报方法的应用和验证。

1 曲面变形技术

曲面变形技术是实现船型优化设计的基础，同时为近似模型训练提供样本船型。本文根据NURBS 技术[1]，通过修改曲面控制网格可以实现曲面变形，该方法使得变形后的曲面仍为NURBS 曲面。如图1所示，在船体曲面生成的过程中，采用ITM和FFD法对曲线控制顶点进行修改，通过变形后的控制网格和基函数计算出变形后的船体曲面。

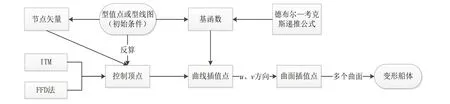
图1 曲面变形技术的程序实现流程Fig.1 Program implementation flow of surface deformation technology

1.1 改进平移法

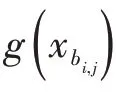
根据修改函数式（1），以曲面v方向某曲线的变形为例，ITM 法原理示意图如图2 所示，f1(x)和f2(x)为变形前后的函数曲线，g(x)为修改函数曲线。针对船体曲面变形，以控制网格点作为输入即可得到变形中的位移大小和方向，再通过曲面重构就可以得到变形船体。以KCS船体曲面变形为例，从图3可以看出，式（1）中x1、x2、α1和α2四个参数含义均有体现，给定参数扰动区间即可实现船体曲面的整体变形。ITM 法的特点是设计变量涉及较少，非常利于船体几何（半船、整船）的修改，并且基于NURBS技术的船体曲面控制网格变换可以保证新船型的光顺性和连续性。

图2 ITM法原理示意图Fig.2 Schematic diagram of ITM method

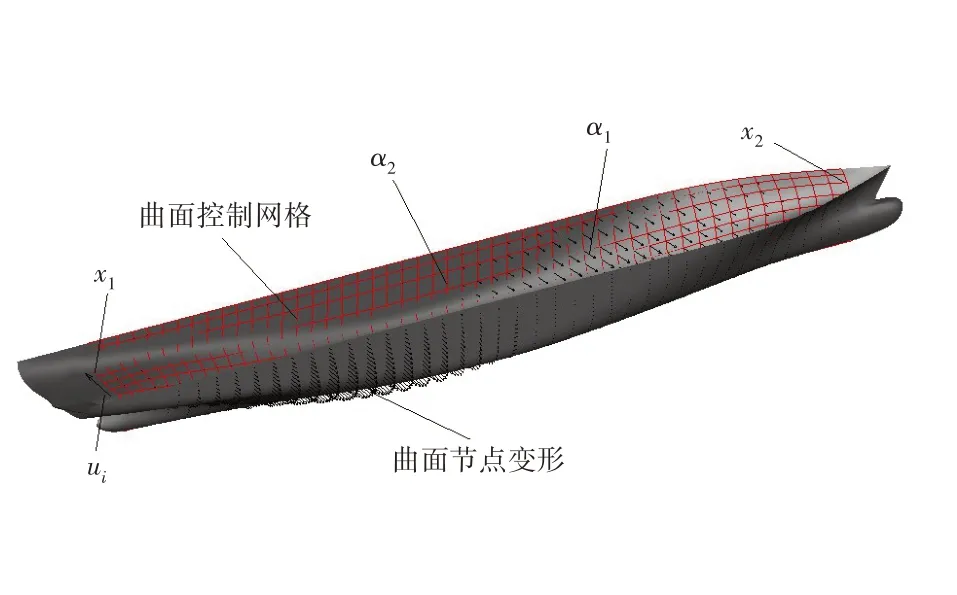
图3 KCS船体曲面变形示意图Fig.3 Deformation diagram of KCS hull surface

1.2 自由变形方法

自由变形（free-form deformation,FFD）方法[3]是Sederberg 和Parry 提出的一种网格自由变形方法。它作为常用的几何造型技术，目前被广泛应用于计算机动画、机器人导航和船体几何重构等领域。

在一个含有待变形物体的长方体中构造局部坐标系O'-STU，在笛卡尔坐标系O-XYZ下的任意点X在局部坐标系中的坐标为(s,t,u)，则有

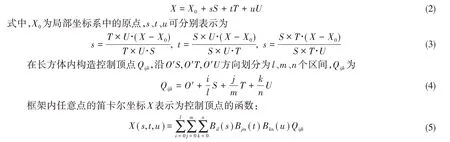
式中，B代表Bernstein多项式基函数，定义为

由式（5）可知，初始船体曲面控制网格点是长方体内控制顶点的线性函数。将部分控制顶点的位置作为设计变量，通过控制长方体框架的变形来达到船体曲面控制网格变形的目的。长方体框架内的船体曲面控制网格点的局部坐标为(s,t,u)，部分控制顶点的位置变化将导致X移动到X'：

如图4 所示，以KCS 球艏变形为例，在船艏处布置控制框架确定曲面变形区域，利用等分数设置框架内控制点位置，控制点在x、y、z方向上的位移控制球艏曲面在三个方向上的变形，如图4（a）所示，在控制框架内的曲面控制网格随着部分控制点的位移而变形，通过曲面正算可计算出曲面节点的变形，如图4（b）所示，船艏纵剖线变形前后对比显示，整个球艏区域变形节点保持协调性。

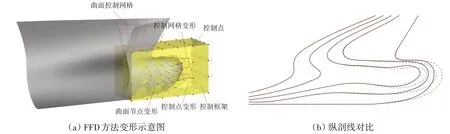
图4 KCS船体球艏变形Fig.4 KCS hull bulbous bow deformation

2 兴波阻力预报

2.1 兴波理论

本文采用C++语言开发，基于Dawson 法的兴波阻力计算步骤[2]，首先在船体表面上用面元法计算叠模扰动流，然后在船体表面和自由面上利用物面边界条件、自由边界条件和辐射条件计算兴波扰动流。计算模型离散如图5所示，把求解的叠模绕流和兴波扰动流问题转化为求解船体表面和自由面分布源点强度问题，有

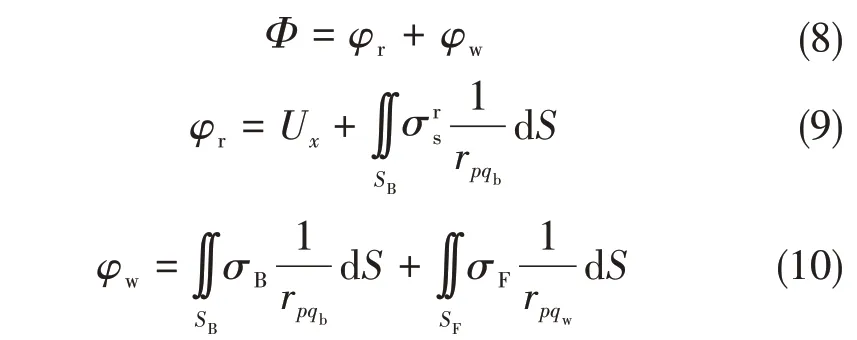
图5 计算模型离散示意图Fig.5 Schematic diagram of discrete calculation model

式中：Φ为总速度势，满足拉普拉斯方程；φr为叠模扰动速度势；φw为兴波扰动速度势；为叠模表面源强；σB和σF分别为船体表面和自由面源强；SB为船体表面；SF为自由面；为场点p到船体表面上点qb和自由面上点qw的距离。

2.2 数值计算验证

以Wigley 和KCS船型作为算例，图6～7为自由面在各方向的加密增长率示意图，自由面采用贴体网格。通过计算域大小变化对结果的影响分析，确定自由面上游扩展0.5L，下游扩展2.5L，y方向延伸1.5L。如图所示对船体首尾部及船宽方向进行了加密。

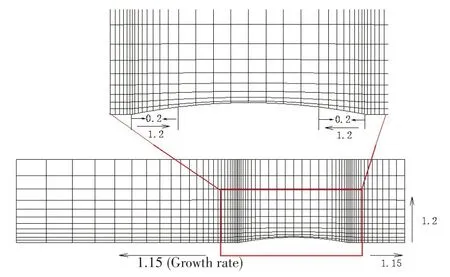
图6 Wigley船型自由面网格示意图Fig.6 Schematic diagram of Wigley ship free surface grid

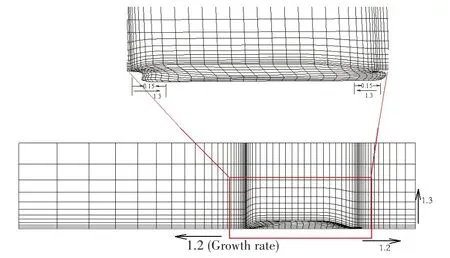
图7 KCS船体及自由面网格示意图Fig.7 Schematic diagram of KCS hull and free surface grid

图8（a）和图9（a）为以自由面横向网格数为变量的兴波阻力系数收敛图，从图中可以看出，随着面元数的增加兴波阻力系数趋近一个值，因此Dawson方法具有较好的收敛性。图8（b）和图9（b）为两种船型兴波阻力系数随不同Fr数下航行的变化曲线，通过对比国内外不同文献的兴波理论计算值，计算结果虽有些不同，但随Fr数的变化较为一致，说明了本文程序计算兴波阻力的可靠性。

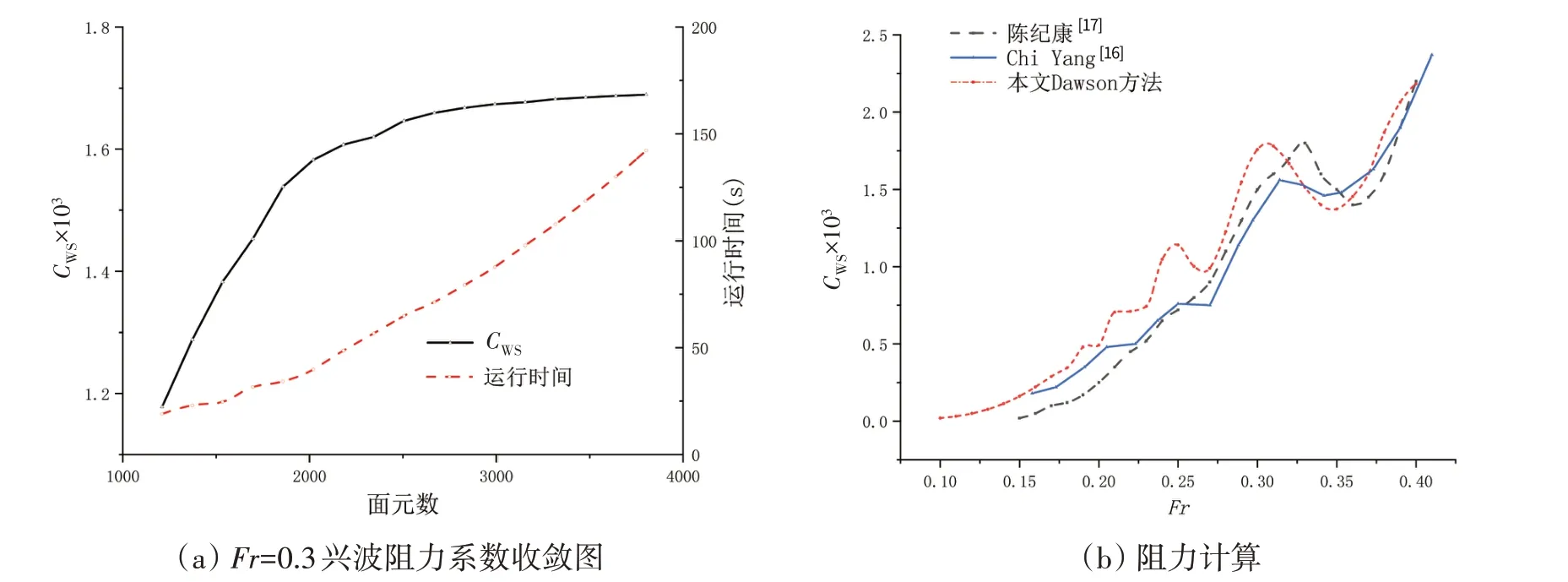
图8 Wigley船型兴波阻力系数Fig.8 Wave-making resistance coefficient of Wigley ship form

图9 KCS船型兴波阻力系数Fig.9 Wave-making resistance coefficient of KCS ship form

3 近似模型

3.1 SLE方法

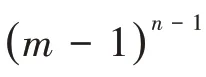
图10 SLE方法样本生成过程Fig.10 Sample generation process of SLE method

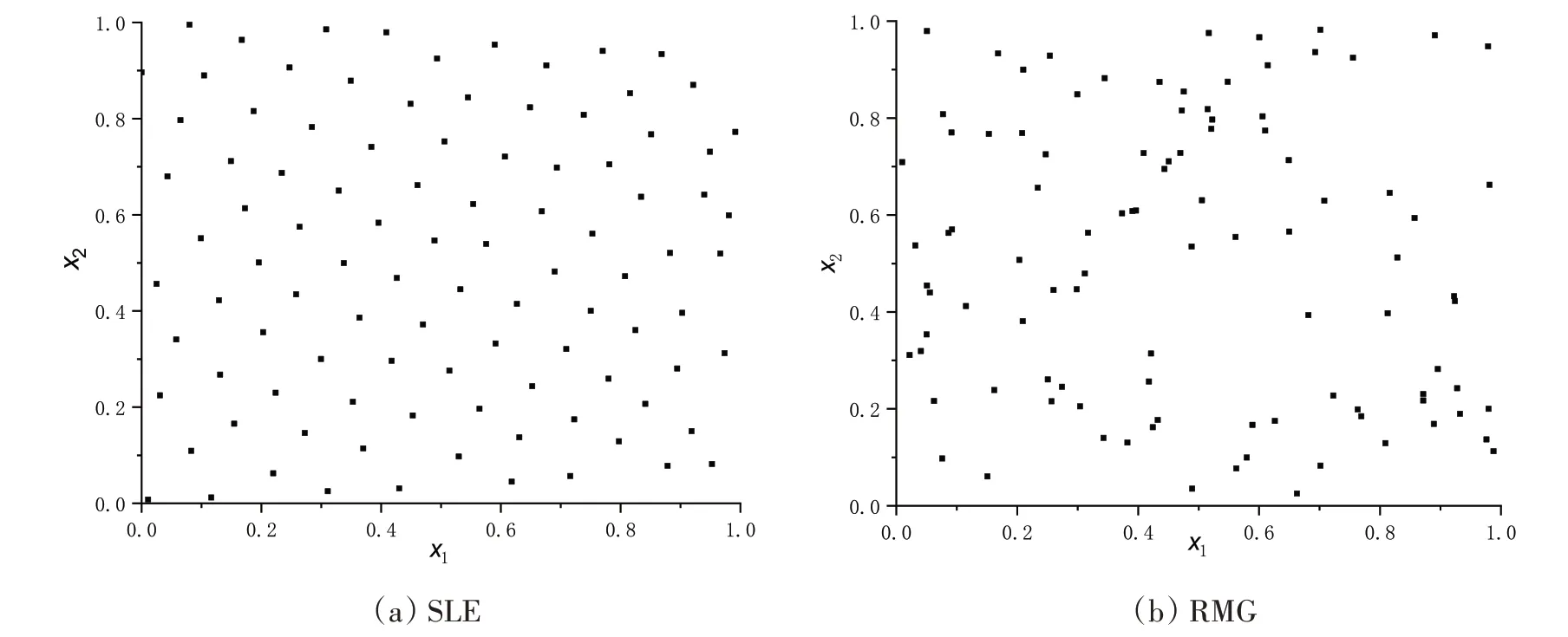
图11 试验样本空间填充性能对比Fig.11 Comparison of filling performance of test sample space

3.2 BP神经网络

图12 为BP 神经网络结构，包含输入层、隐含层和输出层。输入层对当前输入的数据进行处理，隐含层把输入层的数据处理好后传向输出层，输出层给出当此正向传播的输出值和训练误差。步骤如下：

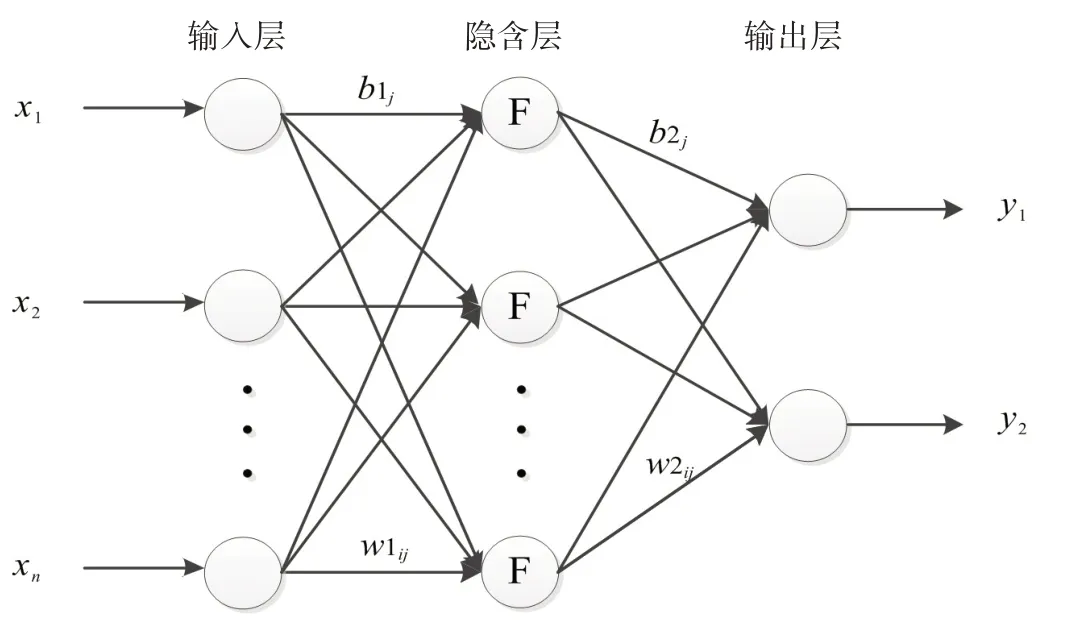
图12 BP神经网络结构Fig.12 BP neural network structure

步骤1：初始化BP 网络参数，包括输入层、隐含层和输出层神经元个数，初始化权值w和阈值b，设置最大训练次数、最小精度和学习率。

步骤2：正向过程计算，通过输入试验样本值，计算各层输出和训练损失函数，如果满足终止训练的要求，则近似模型训练完成，此时神经网络达到预期目标。

步骤3：误差计算，判断是否满足收敛条件。

步骤4：反向过程计算，如果不满足终止条件，将误差反向传输并更新权值和偏置，继续训练。

3.3 近似模型程序设计

如图13 所示，本文通过SLE 试验设计方法和BP 神经网络相结合，建立的近似模型可代替Dawson方法预报船体兴波阻力。

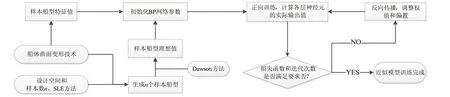
图13 近似模型流程图Fig.13 Flow chart of approximate model

4 KCS船型计算分析

4.1 船型参数化设计

采用ITM 和FFD 方法对KCS 前半部分变形，设计变量如图14 所示，α1和α2控制前半船在船长和船宽方向的变形，dx、dy、dz为控制框架里部分控制点沿着三个方向的位移，表1显示了约束范围均转换为相对于船长的无因次量。采用SLE 方法生成400 个含有5 个特征变量的样本船型，取Fr=0.26 并计算兴波阻力值，从图15中可以看出，较多样本船在兴波阻力方面表现优于母型船。

图14 KCS船体变形示意图Fig.14 Diagram of KCS hull deformation

表1 变形方法参数设置Tab.1 Parameter setting of deformation method

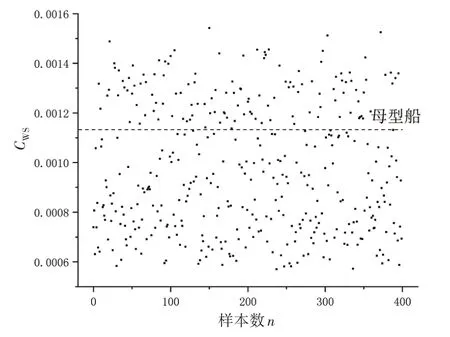
图15 船型样本集Fig.15 Sample set of ship type

4.2 网络参数对性能的影响分析

为了分析不同网络参数对近似模型预测精度的影响，本文选择均方误差Emse和相关系数R2为评价指标：

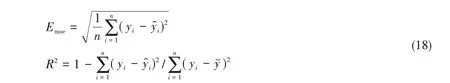
式中，yi、y̑i分别为样本的理想值和预测值，为理想值的平均值，n为样本数。

设网络模型训练样本数为400，最大训练次数为50 000次，训练精度为0.000 01。图16显示的是训练模型评价指标随学习率的变化，可以看出相关系数越大，均方误差越小。如图17所示，隐含层的神经元节点数影响近似模型的预测精度和训练产生的时间成本。根据数据对比结果可看出，本文学习率为0.99时，网络模型的训练性能较好，当隐含层节点数为6层时，相关系数较大，时间成本相对较低。

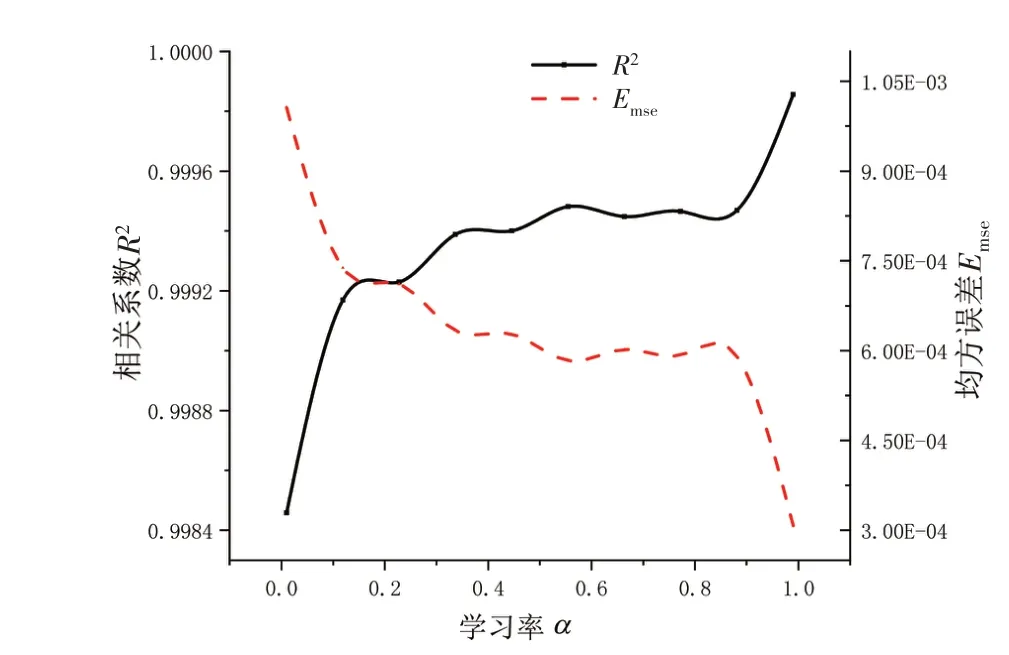
图16 学习率对性能评价指标的影响Fig.16 Influence of learning rate on performance indicators

图17 隐含层节点数对性能评价指标的影响Fig.17 Influence of number of hidden layer nodes on performance

4.3 训练实验及结果分析

隐含层节点数和学习率参数确定之后，按照表2 网络参数开始训练近似模型。为了验证近似模型预测的准确性，在设计空间内，随机生成60 个测试样本船型并计算兴波阻力值。近似模型总误差随训练次数的变化曲线如图18所示，可以看出总误差E逐渐收敛为一个极小值。然后，使用训练之后的近似模型对测试样本船型集的60组样本进行预测，图19为测试样本预测值的相对误差统计图。

表2 近似模型结构参数Tab.2 Structure parameters of approximate model

图18 训练次数与总误差的关系Fig.18 Relationship between training times and total error

图19 测试样本的相对误差变化Fig.19 Relative error variation of the test sample

利用训练好的模型对60 组测试样本Cws进行预测，平均相对误差为0.282%，相关系数R2为0.9998，均方误差为3.14E-04，运行时间为2 ms。其中，部分测试样本的网络输出如表3 所示，表中输入数据为归一化后的值，通过分析表明，本文构建的智能预报方法预测样本船型的兴波阻力的精度高且速度快。

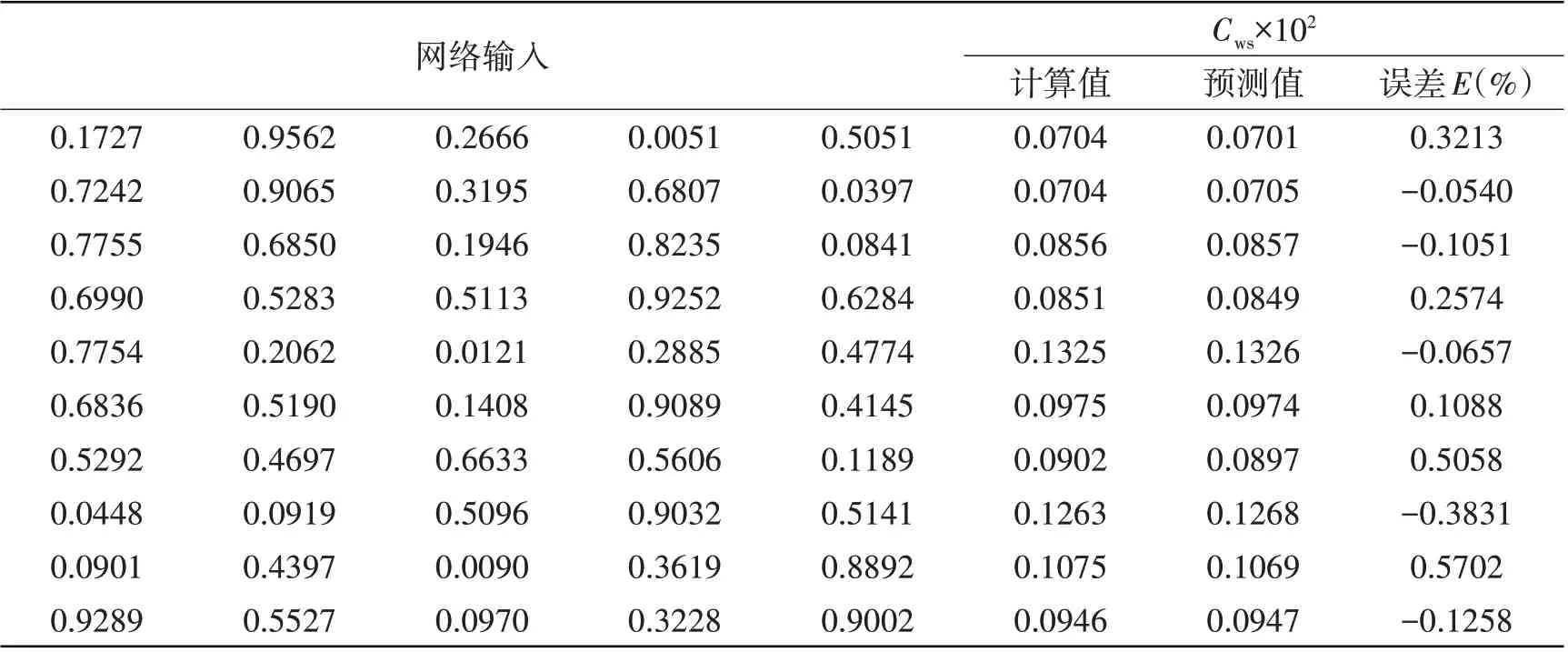
表3 测试样本的网络输出Tab.3 Network output of test samples

5 结 论

本文建立了基于样本船的兴波阻力智能预报方法，结合曲面变形技术和兴波阻力预报技术，实现了在设计空间内船体兴波阻力的快速预报，并对近似模型的相关参数和训练展开分析，得出如下结论：

（1）提出了基于曲面控制网格的曲面变形方法，编写了ITM 和FFD 方法的曲面变形程序，对KCS船型进行参数化设计并生成样本船型集。

（2）在曲面变形技术和兴波阻力预报技术基础上，通过SLE试验设计方法和BP神经网络相结合，建立的近似模型可快速预报船体兴波阻力，耗时成本为毫秒量级。

（3）通过网络模型参数分析和训练，测试样本预测值相关系数为0.9998，均方误差为3.14E-04，本文近似模型的预测精度较高。