有限水深多载荷作用下细长圆管水动力响应试验研究

陈志雄，臧志鹏，王 琮，张庆河，张金凤

（1.中国直升机设计研究所，江西 景德镇333001；2.天津大学 水利工程仿真与安全国家重点实验室，天津 300072；3.中国石油集团工程技术研究有限公司，天津 300451）

0 引 言

隔水导管是海洋石油勘探开发中被广泛采用的一种关键设备，在复杂海洋环境荷载及作业荷载的周期作用下，会发生周期性振动，如涡激振动[1]（VIV，vortex induced vibration）、波致振动等，这将导致隔水导管结构发生疲劳损坏甚至断裂，因此研究隔水导管的水动力响应一直是一个热门课题。

关于海洋隔水管水动力响应的研究，学者关注较多的是水流作用下隔水管产生的“涡激振动”现象。在对涡激振动的机理研究中，Feng[2]、Williamson[1]、Khalak[3]等人进行了大量工作，包括“锁定”[2]现象发生的条件、质量比对VIV 的影响、尾涡脱落模式等，这为后续开展涡激振动的研究提供了理论基础。对于实际海洋工程中隔水管涡激振动的研究，当前学者更偏向于深海柔性管，这种情况下隔水管振动的主要特点是高阶和多模态振动，因此振动幅值和频率的规律也更加复杂，例如Trim 等[4]开展的长细比为1400 的VIV 相似实验，Chaplin 等[5]开展的阶梯流情况下长径比为469 的柔性管VIV 实验，均获得了高模态下的VIV 特性，其中Chaplin 实验中隔水管横向振动模态可达到八阶。而对于大陆架附近海域的工程环境，目前对隔水管的水动力研究还较少，该区域作业水深在100 m 左右居多，波浪工况通常满足1/20≤h/L≤1/2，其中L是波长，h是水深，这在波浪理论中属于有限水深波浪的范畴。在有限水深条件下，隔水导管结构虽不具有较强的柔性，但受波浪和水流的作用都比较明显，VIV 与波致振动对隔水管的疲劳损伤都不可忽视。在有限水深条件下，一些学者也开展了考虑多种荷载条件下隔水管的振动响应研究，如郭海燕[6]、娄敏[7]等研究了内流、外流和顶张力作用下隔水管的涡激振动响应，发现内流流速的增大更容易导致VIV 锁定现象，隔水管的固有频率与顶张力成正比等，但在实验研究中考虑波浪荷载作用的还较少。

本文针对有限水深下的自升式钻井平台隔水导管运动特性，将隔水管简化为细长直立圆管，开展了综合考虑水深条件变化以及顶张力、波浪和海流等多荷载共同作用下的隔水管实验研究，对前人的研究进行了一定补充，同时对大陆架海域附近隔水管安全作业具有一定的工程指导意义。

1 试验方法

1.1 试验布置及工况

本试验使用的波流水槽长50 m、宽1 m、深1.5 m，水深1 m 的条件下流速可达到0.25 m/s，波高范围为0～0.2 m。实验原型水深为80 m，确定几何比尺为1:100，采用弗劳德数相似准则。实验中圆管的下端固支于水槽底面，上端采用双滑轮夹紧，使得圆管不发生扭转，同时允许立管端部在垂向上自由滑动，使圆管顶部施加的拉力可传导至圆管下端，其试验布置如图1所示。

图1 水槽中试验装置的布置Fig.1 Arrangement of the test device in the flume

圆管模型尺寸长为0.98 m，外径为8 mm，长径比为122.5，经过强度对比最终选用柔性适中的PVC材料管，测得其相关的材料特性参数，并依此计算了圆管截面惯性矩及抗弯刚度等参数，见表1。

表1 圆管模型力学性能参数Tab.1 Mechanical properties of the test pipe

试验中针对我国南海自升式钻井平台的主要作业荷载范围，通过模型比尺转换，获得模型试验的参数条件：波高H为0.04～0.16 m，波周期T为0.9～1.6 s，流速U为0.07～0.22 m/s，轴向拉力P为1～5 N，试验中设置试验组次时，波高、周期、流速、轴向拉力的变化梯度分别为0.02 m、0.2 s、0.05 m/s 和2 N。本试验原型水深为80 m（试验水深0.80 m），考虑潮位变化以及平台升高等引起的立管相对水深减小情形，另外设置了2组水深为0.5 m和0.65 m，以定性研究相对深水的影响。考虑到实际海洋工程中隔水管内部多数工况下是充满液体的，本试验中在未特殊说明情况下管内是充满水的。试验中波浪和水流同向，荷载条件工况组合见表2。

表2 试验工况Tab.2 Test conditions

1.2 数据采集方法

本实验采用光纤光栅应变传感器（FBG）对圆管的运动响应进行测量。光纤光栅传感器具有体积小、测试数据准确等优点，布置于圆管模型上不会对实验结果造成影响，不少学者采用该传感器采集圆管的振动信号[8-9]，实验证明该传感器采集信号可靠性较高。试验中光纤直径为0.5 mm，每根光纤上沿圆管长度方向以25 cm 为间隔串联布置4 个应变测点（应变测点直径与光纤相同），编号为#1～#4；沿圆管环向表面以90°为间隔共均匀布置4条光纤，编号分别为IL1、IL2、CF1 和CF2，其中IL代表顺流向（in line），即波浪水流运动的方向；CF 代表横流向（cross flow）。应变传感器的采集点数量为16 个，示意图见图2。光纤光栅传感器的采样频率为500 Hz，足以捕捉圆管所有频率的振动数据。试验中光纤光栅传感器随圆管一同变形，引起光波波长变化，基于波长与应变的对应关系，利用光纤光栅调解仪即可得到应变数据，最终通过模态分析法（公式（5）～（7））可将应变转化为振动位移。试验时，先设置实验参数，待波浪水流稳定后，持续采集30 s的实验数据。

图2 应变传感器布置示意图Fig.2 Arrangement of the FBG strain sensors

2 数据分析方法

2.1 频率分析法

当圆管进行周期性的振动时，其振动可以看做由简单频率的简单振动的叠加，这一物理过程可以用傅里叶（Fourier）级数的展开来描述[9]：

2.2 模态分析法

3 试验结果分析

3.1 典型工况分析

试验过程中，待波浪和水流稳定之后，开始采集应变数据。本试验采用了单点流速仪，测点位于静水面下20 cm 处。图3为典型的波高以及流速数据历程曲线，分别显示了单独波浪（T=1.2 s，H=0.06 m）条件下的波高历程和单独水流（U=0.22 m/s）以及波流联合（U=0.22 m/s，T=1.2 s，H=0.06 m）条件下静水面下20 cm处的流速历程，可以发现应变数据采集过程中波浪以及流场均已达到稳定状态。典型工况下对应的IL 向和CF 向位移随时间的历程曲线如图4 所示。图中分别显示了水深h=0.8m 空管条件下，三种工况下圆管测点2#处的位移历程曲线。从历程曲线中可以发现，单独波浪和水流作用下，圆管振动频率单一，而波流共同作用下，其位移历程存在多种频率的振动参与。其中，单独水流作用下，IL 向的振幅整体上比CF 大，这说明涡激振动还未发生“锁定”[2]现象，此时涡脱落频率离涡激振动锁定频率区间还较远，而由于IL向的振动频率是涡脱落频率的两倍[11]，其频率更有可能接近或者处于锁定频率区间，因此其幅值会更高，这在后文中会进一步分析。

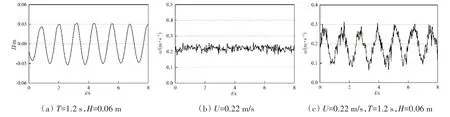
图3 典型工况下波高及流速历程曲线Fig.3 Wave height and velocity history under typical conditions

图4 典型工况下IL向和CF向位移历程曲线Fig.4 Displacement history in IL and CF directions under typical conditions

图5 典型工况IL向和CF向振动数据频谱分析结果Fig.5 Spectrum analysis results of vibration data in IL direction and CF direction under typical conditions

图6 h=0.8 m时，圆管自然状态下的频谱分析结果Fig.6 Results of frequency spectrum analysis of the pipe in natural statewhen h=0.8m

3.2 振动位移幅值响应特性

通过频谱分析发现，本试验中圆管模型的振动模态基本为一阶，考虑波流作用下的复杂流速情况，模态分析时取最高参与模态为二阶，即N=2，最终得到圆管上任意点位移的时间变化历程。对每一点的位移随时间历程数据求均方根值（即RMS值），可得到圆管RMS值沿水深方向的分布，如图7 所示。可以发现，在波浪、水流以及波流共同作用下，圆管IL 向的RMS值都要比对应工况下CF 向的值大，这与上文的位移时间历程的分析得到的结果一致。在实际海洋工程中，往往更加关注隔水管的最大变形，因此，本文将主要分析IL向振动幅值，针对每一个工况，取IL 向最大RMS值与管径D的比值作为振动幅值，用A/D表示。

图7 典型工况下圆管RMS值沿水深分布Fig.7 Distribution of RMS value along water depth in typical conditions

3.2.1 单独波浪作用

波浪作用下，圆管振动状态受波高与波周期共同影响，本小节分析了水深h=0.8 m（h/L=0.82）时，波高H/D=5、H/D=7.5、H/D=10和H/D=12.5的条件下，圆管振动幅值随波频率fw的变化规律，其中波频率通过取fw/fn（由图6可知管内充水时fn=8.7 Hz）进行无量纲化，结果如图8所示。从图中可以发现，在相同波频率下，波高越大，圆管幅值也越大。这是比较好理解的，根据微幅波理论可知，波高越大，波浪作用于圆管上的动压越大，圆管整体的受力更大，因此圆管振动幅值更大。还可以发现，随着波频的增大，圆管的幅值出现了先增大后减小的趋势，在fw/fn≈0.1时，相同波高条件下，圆管的幅值最大。为研究圆管最危险幅值，后文在进行波浪研究时取波浪特征频率fw/fn≈0.1。

图8 单独波浪作用下圆管位移幅值随波频的变化Fig.8 Variation of displacement amplitude of the pipe with wave frequency under single wave action

3.2.2 波流共同作用

实际海洋环境中，潮流与波浪是同样典型的水动力因素，比如我国南海区域呈现典型的全日潮特征[15]，一天会经历一次涨潮与落潮，当潮流与波浪同时发生时，隔水管的振动便会受波流共同作用的影响。本小节采用波频率fw/fn=0.1，固定流速Vr=1.72的波流共同作用的条件，比较单独波浪和波流共同作用情况下圆管的幅值变化特性，如图9 所示。从图中可知，单独波浪与波流共同作用下，振动幅值与波高都是呈正相关的。与单独波浪作用下相比，波流共同作用下圆管的振动幅值要小，这是因为加入的固定流速Vr=1.72 比较小，在IL 向产生涡激振动强度很弱，而此时由于水流的拖曳力影响会导致圆管沿顺流向产生一定的初始变形，这使得圆管模型相当于处于拉伸状态，继而导致圆管的振动幅值总体上减小。需要指出的是，当流速较大时，拖曳力导致的变形对振动的影响将相对较小，此时IL向水流导致的涡激振动以及波致振动幅值会出现叠加，比单独波浪作用下的幅值大，这从3.1 节典型工况分析中可以看出。

图9 波流共同作用下圆管位移幅值随波高的变化Fig.9 Variation of displacement amplitude with wave height of the pipe under combined wave and current action

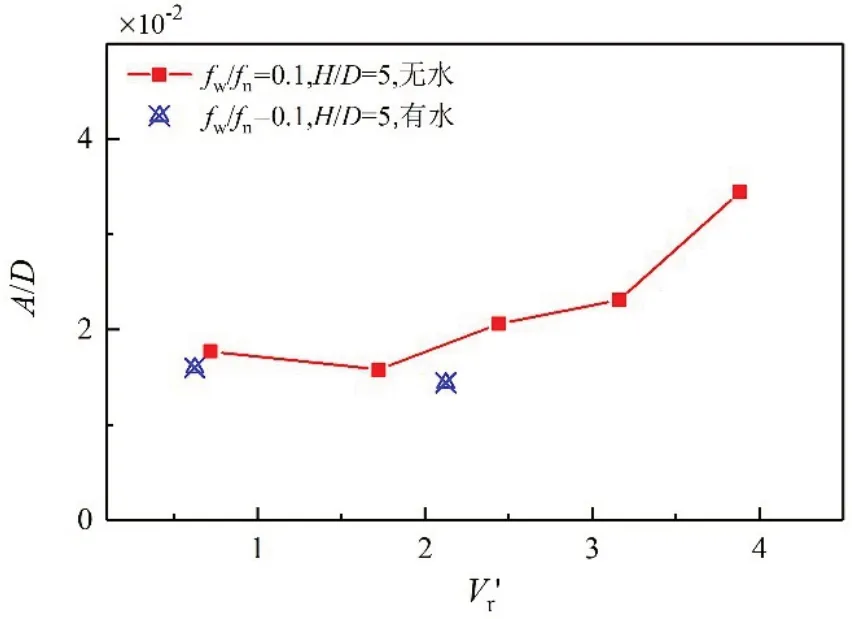
图10 波流共同作用下圆管位移幅值随流速的变化Fig.10 Variation of displacement amplitude with velocity of the pipe under combined wave and current action

3.2.3 轴向拉力作用

海洋钻井隔水管作业过程中为防止隔水管自身因为受压而发生压溃，同时为提高隔水管的抗弯强度，钻井平台往往会给其顶部施加一定的张力。本小节分析了波频率fw/fn=0.1，波高H/D=5、10和15的条件下，圆管振幅随轴向拉力P/G（其中G为管内充满水时圆管的重力）的变化，结果如图11 所示。从图中可知，随着轴向拉力的增大，三种波高条件下圆管振幅都呈减小趋势，轴向拉力对圆管的振动幅值有明显的抑制作用，这是因为轴向拉力提升了圆管的刚度，导致圆管的振动幅值减弱。还可以发现，当轴向拉力P/G从5增大到8.2时，幅值的变化幅度较小，因此从工程角度来考虑，为提升隔水管抗弯强度，只需施加合适的轴向拉力即可，过大的轴向拉力并不会取得较明显效果，相反会造成平台荷载过大。

图11 单独波浪作用下圆管位移幅值随轴向拉力的变化Fig.11 Variation of displacement amplitude of the pipe with axial tension under single wave action

3.2.4 变水深影响

对于自升式钻井平台而言，极端波高的出现、海潮的涨落以及平台自身因作业需要而进行的上下调整，都会改变隔水管水上和水下长度的分布，因此本实验研究了水深变化时圆管振幅随波浪因素的变化。图12为波频率fw/fn=0.1，水深h/L=0.82、0.66和0.51时，圆管振幅随波高的变化规律。从图中可以发现，随着水深减小，圆管整体上的振幅并不随之减小，其中水深h/L=0.66时，圆管整体上的幅值最大，即在相同波浪条件下，水深h/L=0.66时圆管振幅最大，这是因为波浪是一种表面波，波浪对圆管的作用力主要分布在水面附近，如果将波浪力等效成一个合力（忽略水深对该合力大小的影响），那么水深的减小势必导致该合力的等效作用点下移，本实验的圆管模型可简化为简支梁，波浪力的合力的等效作用点越靠近圆管中心，圆管的振动幅值也将越大。相比其它水深，本实验中水深h/L=0.66时波浪力的等效作用点更靠近圆管中点，因此幅值更大。

图12 单独波浪作用下水深变化对圆管位移幅值的影响Fig.12 Influence of water depth variation on displacement amplitude of the pipe under single wave action

水深的变化会导致波浪力等效作用点的变化，这对圆管最大振动幅值出现的位置也将产生影响。本文针对波频率fw/fn=0.1、波高H/D=15的工况，分析了水深h/L=0.82、0.66和0.51时圆管RMS值沿水深的分布，如图13 所示。从图中可知随着水深的减小，圆管最大位移点逐渐下移，当水深h/L从0.82 减小至0.51时，最大位移点水深z/L从0.54减小至0.47，这种变化幅度并不是很大，但对于海洋工程中隔水管这种由多节组成的圆管结构来说，避免最大振动幅值出现在管节连接处对隔水管安全作业具有重要意义。

图13 单独波浪作用不同水深条件下圆管RMS值沿水深的分布Fig.13 Distribution of RMS value of the pipe along water depth under single wave action and different water depths

3.3 特征点水平面内运动轨迹

为研究圆管在多荷载作用下的运动形态特征，本节分析了水深h/L=0.82 时测点#1、#2、#3、#4 在（a）单独波浪（h/L=0.82，fw/fn=0.1，H/D=10）、（b）波流共同（h/L=0.82，fw/fn=0.1，H/D=10，Vr=1.72）、（c）轴向拉力（h/L=0.82，fw/fn=0.1，H/D=10，P/G=8.3）和（d）变水深（h/L=0.51，fw/fn=0.1，H/D=10）作用条件下的运动轨迹图，结果如图14所示，其中IL向和CF向的位移幅值分别用Ax/D和Ay/D表示。

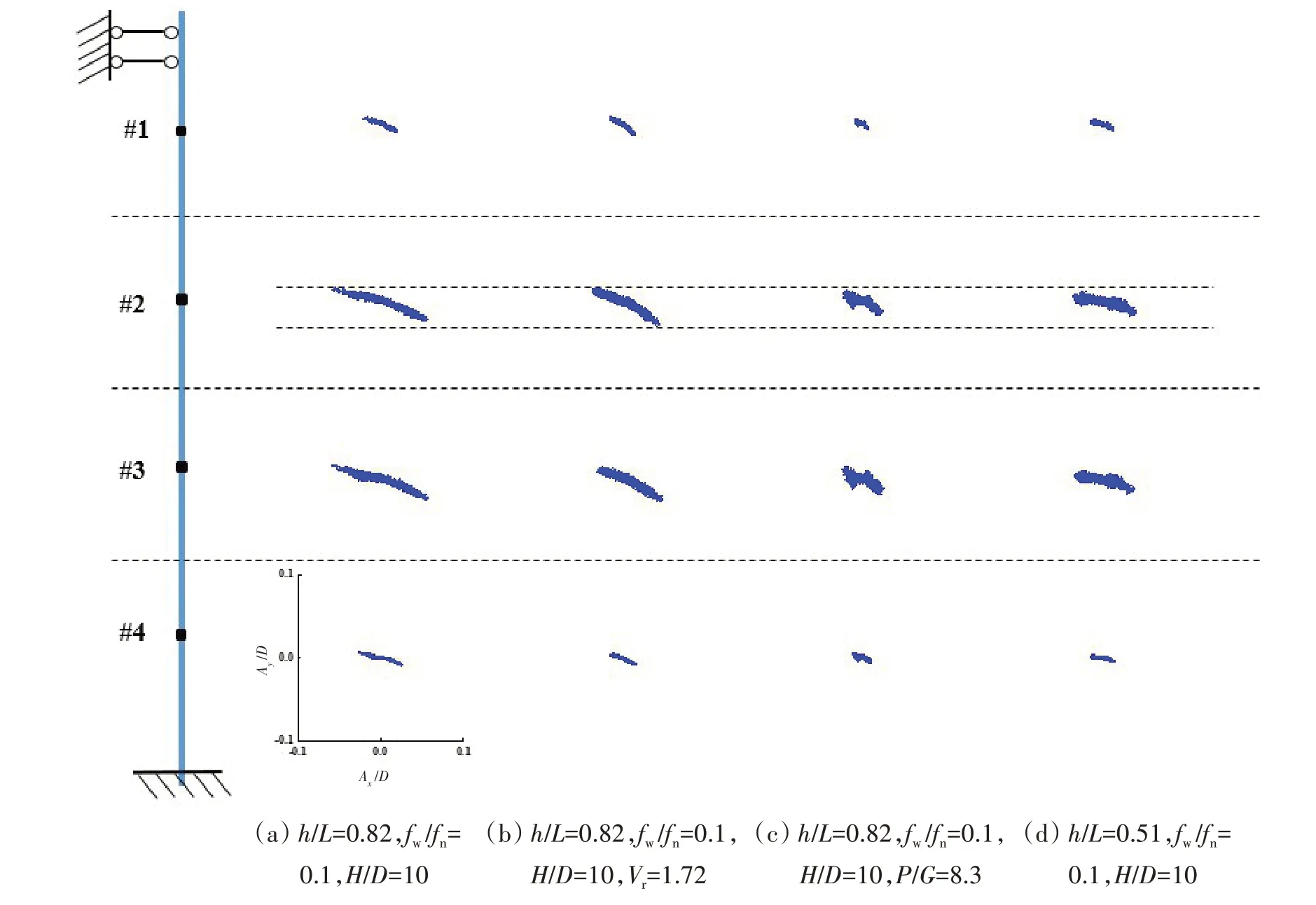
图14 不同工况条件下圆管各测点运动轨迹Fig.14 Trajectory of each measuring point in the pipe under different conditions

从四种工况各测点轨迹的形态来看，轨迹均呈斜“一”字形，这是因为本实验过程中，波浪作用下圆管IL方向的振动干扰并且主导了CF方向的振动，CF和IL方向响应频率相同，所以测点呈斜“一”字形运动轨迹。波流共同作用的工况中由于加入的固定水流流速较小，CF 向的涡激振动强度远小于IL向受波浪主导的振动强度，因此CF 向的振动同样受IL 向干扰和主导，最终CF 和IL 方向响应频率相同，测点也以斜“一”字形运动，这种现象与Mao 等[17]在研究剪切流作用下隔水管的涡激振动实验中得到的结果相似，其实验中当剪切流流速较小时，CF方向对IL方向的振动干扰并主导了IL方向的振动，测点也出现了斜“一”字形轨迹。

从四种工况各测点轨迹的幅值来看，可以发现靠近圆管中间位置的测点2#和3#处的运动幅值较大，而圆管靠近支座两端的测点1#和4#则较小，这与前面的模态分析以及位移RMS值沿水深分布的结果一致。通过四种工况的运动轨迹幅值的对比可以发现，相比于单独波浪作用，波流共同作用、施加轴向拉力、以及水深由0.8下降至0.5的工况条件下，各测点IL向的运动轨迹幅值明显减小，这与3.2节中分析的结果一致。对于CF 向运动幅值，这里以测点2#为例，从图中可知，相比于单独波浪作用，施加轴向拉力、以及水深减小的工况条件下，CF 向幅值也是减小的，而波流共同作用下，由于水流的涡激振动作用的叠加，CF向幅值有所增大。

4 结 论

本文在有限水深条件下，开展了不同水深中波浪、海流、轴向拉力多荷载作用下细长直立圆管的水动力响应试验，通过对采集得到的振动数据进行频率及模态分析，获得了圆管的频率和振动最大位移幅值的变化规律，以及圆管特征点的运动轨迹特性。得到的主要结论如下：

（1）在本模型实验中，由于流速较小，CF向涡激振动未发生锁定，波、流以及波流共同作用下IL向的振动都影响并主导着CF向的振动。波流共同作用下，圆管的振动频率同时受波浪频率和涡激振动频率控制，其中涡激振动由于波浪的周期性作用存在多频参与现象。

（2）圆管的最大位移RMS值随波高的增大而增大，轴向拉力对圆管的振动起到良好的抑制作用。波流共同作用下，当固定流速较小时，由于水流拖曳力作用导致的圆管初始变形使得圆管幅值与单独波浪作用下相比降低，但流速较大时则相反。实际工程中存在相对危险的水深，使得单独波浪作用下圆管整体位移幅值最大，本实验中相对危险水深为h/L=0.66。

（3）由于圆管IL方向的振动对CF方向振动的干扰与主导，本实验中CF 和IL方向响应频率相同，圆管测点呈斜“一”字形运动轨迹。与单独波浪作用下相比，继续施加轴向拉力、减小水深至危险水深以下，各测点IL向和CF向的运动幅值均明显减小，而继续施加较小水流条件下，CF向幅值有所增大，IL向幅值明显减小。