含孔洞岩样中超声波传播特性的数值模拟研究★
2022-08-12高结旺黄宜超邹杰平
高结旺,黄宜超,邹杰平
(江西理工大学资源与环境工程学院,江西 赣州 314000)
随着社会经济发展和人民物质需求的日益增长,国家对于地下资源开采和建设逐渐加大。而岩土体在自然条件下,风化作用导致其内部常存在大小、形状不一的宏微观缺陷,这种自身存在的缺陷给岩土体安全稳定带来潜在的危害,而在人为扰动、地震等外界因素影响下进一步加剧了岩土体的失稳破坏,时常给地下施工带来巨大的生命财产安全威胁[1-3]。因此,对岩土体缺陷结构特征超前感知与识别,可以为地下工程施工提供宝贵的工程经验[4-6]。
近些年,超声波探伤等技术被广泛的运用在地下岩土工程中。通过分析超声波在岩土体传播过程中的声学参数与岩土体结构特征等之间的关系,可以识别地下岩体结构、构造等基本情况,为减少因地下施工所带来的安全事故提供前期准备[7]。M.Kumar等[8]研究发现当介质孔洞尺寸远小于声波波长时,孔洞形状是影响声波波速的关键。在此基础上C.Scotellaro等[9]研究指出相比于缺陷其他特征对声波波速的影响而言,缺陷形状特征表现的最明显,岩体刚度与缺陷纵横比呈正相关,而波速应力敏感性则与缺陷纵横比呈负相关。G.T.Baechle等[10]研究发现,波速与小孔洞相关性相比于大孔洞更明显。Weger等[11]更进一步对影响声学参数的缺陷特征进行细化的研究,发现相比缺陷其他特征而言,声学参数对孔隙结构复杂性和大孔洞孔径综合效应更敏感。刘向君等[12]研究了孔洞密度对声学参数之间的表征关系,指出声波波速和波幅与孔洞密度呈负相关性,并且波幅的变化相对于波速的变化更明显。梁利喜等[13]基于波动理论和有限差分理论,分别研究了孔洞密度、分布、形状对声波衰减系数影响,发现孔洞密度对声波衰减系数产生最大影响。
大量研究者从室内试验和数值模型研究了超声波在介质中传播特性,并指出超声波衰减系数、振幅、波速、相位对孔洞结构的变化更敏感[14]。但目前对于超声波在介质中传播规律的数值模拟研究主要集中在二维数值模型,很难真实的反映超声波在地下岩土体三维空间中的传播规律。为深入研究含孔洞岩样中超声波传播特性,利用COMSOL软件分别建立了不同孔洞尺寸、角度、形状三维孔洞压力声学模型,分别从超声波透射信号、波幅透射系数、声压快照图、声压极大值四个方面分析超声波传播规律。为下一步原位声波识别复杂的洞缝组合结构提供理论依据。
1 数值模型的建立
采用φ50 mm×100 mm圆柱体岩样模型,岩样密度2 817 kg/m3,超声波波速为2 500 m/s。COMSOL数值建模流程如下:1)根据需要求解问题类型选定恰当的物理场研究;2)建立三维孔洞模型并定义求解区域的材料属性,施加声波边界条件后对三维孔洞模型进行网格剖分;3)边界条件设定好后对模型进行瞬态求解计算。通过分析模型计算结果中超声波透射信号、波幅透射系数、声压快照图、声压极大值的规律,反演得到超声波在孔洞模型中传播特征规律。
1.1 模型简化假设
为了便于研究超声波在介质中传播规律问题,传统的方法常假设介质为各向同性均质材料,及介质的力学和材料性质与空间位置无关[15-16]。
1.2 控制方程
模型不考虑温度方程的情况下,压力声学瞬态研究的控制方程为:
(1)
其中,ρ0为介质密度;p为声压;q为偶极源;c为介质中声速;t为时间;Qm为单极源。
1.3 模型的建立
选用COMSOL数值软件压力声学物理场模块,在瞬态时域条件下探究超声波在缺陷岩体中透射规律试验。为了达到数值试验目的,如表1所示,利用带有规则孔洞岩样模型代替缺陷岩体,分别探究孔洞形状、尺寸、角度三种因素对超声波透射的影响,进而反演得到超声波在缺陷岩体中传播特征规律。
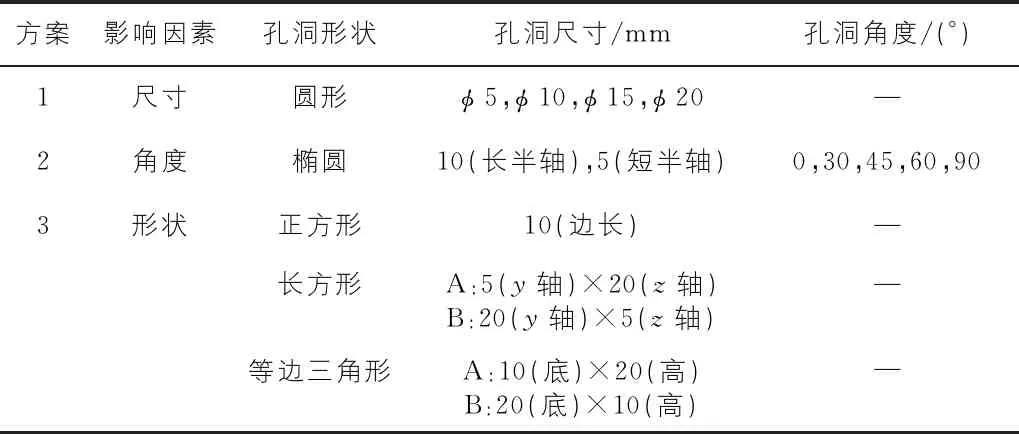
表1 孔洞缺陷模型几何参数
1.4 边界条件设置
由于设置合理的初始边界条件决定着模型最终计算结果精度,因此含孔洞岩样模型超声波透射数值试验初始边界条件设置主要有如下几点:
1)设置孔洞模型表面与内部最初声压场为零。
2)设置模型侧面边界与底部边界为完美匹配层边界。
3)模型顶部为声压入射边界,利用高斯脉冲函数信号作为激励源调控声压大小。使用脉冲力去描述超声波的产生是一种简单常见的方法,如在钢轨超声波检测中常用高斯脉冲函数描述脉冲信号触发[17]。因此,选择高斯脉冲函数信号作为超声波激励源。高斯脉冲函数信号的表达式为[18]:
(2)
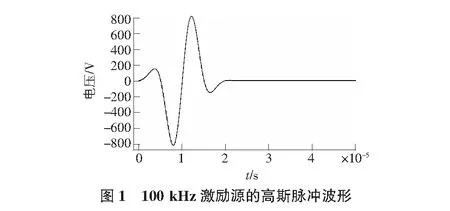
其中,ω0=2πf为脉冲信号的中心角频率;U0为脉冲电压;Δt为脉冲延时;σ2为控制脉冲宽度。声波激励源的发射频率选用100 kHz高斯脉冲信号,激励信号的时域波形图如图1所示。
1.5 网格划分
在利用有限元COMSOL软件进行模型求解时,模型网格划分需根据求解问题类型来确定。为了得到超声波在含孔洞模型传播过程中解析波这特殊问题,常规的网格划分会导致模型计算出现精度低甚至不收敛的现象。为了精确求解含孔洞模型中超声波传播过程中解析波,采用奈奎斯特准则来严格限制模型网格的划分[19],如式(3)所示,采用模型网格最大单元大小最大不能超过声波波长1/10来限制模型网格的划分。
(3)
其中,L为模型最大单元大小;v为超声波波速;fmax为超声波最大频率。
2 结果与分析
2.1 孔洞尺寸对超声波传播特性的影响
图2为岩样孔洞形状为圆形、孔洞尺寸大小分别为0 mm,5 mm,10 mm,15 mm,20 mm的模型透射信号曲线。分析得到超声波在介质传播过程中声压波幅与孔洞尺寸呈现明显的负相关,即模型孔洞尺寸越大,声压波幅越小。如当模型为完整时,声压波幅为390 Pa;孔洞大小为10 mm时,声压波幅为337 Pa;孔洞大小为20 mm时,声压波幅为235 Pa。出现该现象原因在于介质中孔洞对超声波传播产生了散射、绕射、放射等干扰现象,导致超声波能量在介质传播过程中产生损失,致使声压波幅出现大幅下降现象。

当模型中存在孔洞时,由于超声波在传播过程中介质属性发生改变,声波能量必定发生不同量级的损失。因此引入波幅透射系数α来定量的表征超声波衰减,如式(4)所示:
(4)
其中,α为波幅透射系数;Ai,A0分别为有孔洞和无孔洞模型接收信号幅值。波幅透射系数越接近1,则超声波能量在缺陷岩体内衰减度越小,即超声波透射性能越好。
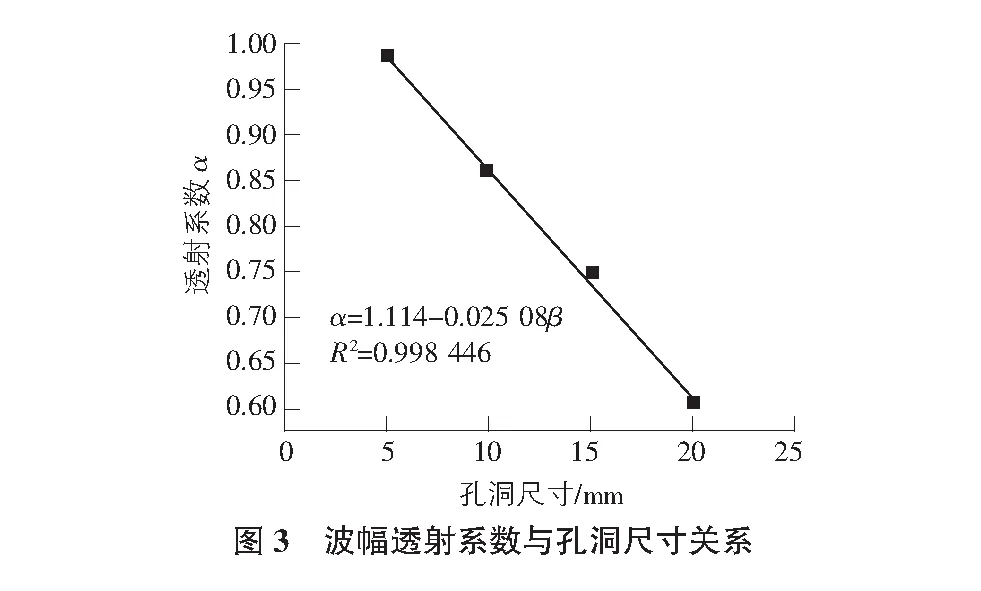
图3为透射系数α与孔洞尺寸的拟合关系曲线,分析发现模型孔洞大小与波幅透射系数α存在线性关系,线性拟合相关系数R2达到0.998。当完整模型波幅透射系数为1,说明超声波透射过程中没有发生衰减现象;而当孔洞尺寸为5 mm时,透射系数衰减到0.987较无孔洞下降了1.3%;孔洞尺寸增大为20 mm时,透射系数进一步衰减到0.607较无孔洞下降了39.7%。这说明超声波在模型传播过程中,超声波透射能力极易受孔洞大小的影响,即模型孔洞尺寸越大,超声波透射系数越低,超声波能量衰减越大,相应超声波透射能力越低。
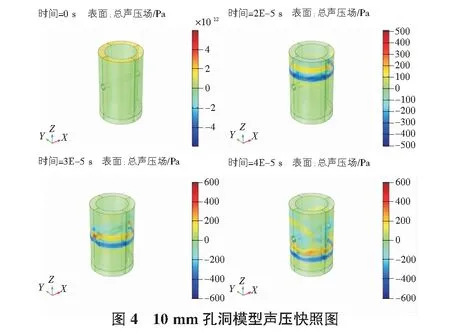
通过对透射边界上超声波透射信号和透射系数研究,验证了孔洞尺寸大小会干扰超声波的传播并且产生严重的能量损失。为了深入分析超声波在孔洞模型传播过程中声压分布规律,选取10 mm孔洞模型中声压快照图(见图4)。发现超声波在孔洞模型传播过程中声压分布随时间的变化主要分为两个阶段:第一阶段,声波从入射边界传播到孔洞之前时,声波声压分布呈现有规律的直线传播,在此期间没有出现绕射、反射现象;第二阶段当声波传播穿透过孔洞到达接收边界时,由于传播介质的变化,致使声波在介质中的传播发生明显的绕射、反射现象。
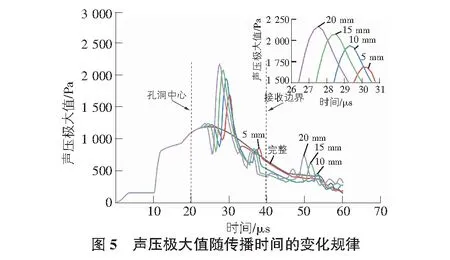
在声波传播过程中模型孔洞尺寸不仅会对声压分布产生影响,也会对声压大小产生一定的影响。为了研究孔洞尺寸对超声波传播过程中声压大小的影响,提取了五种孔洞尺寸模型下超声波声压极大值与时间关系曲线(见图5)。发现可以把不同孔洞尺寸模型声压极大值的时变规律分成三阶段:传播时间0 μs~20 μs期间为第一阶段,由于在此阶段五种不同孔洞尺寸模型超声波传播并未透过孔洞,所以各模型声压极大值重合成一条曲线且当传播时间达到20 μs时均达到1 095 Pa。原因是此阶段超声波在各孔洞模型传播过程中,声压极大值由于介质振动数量和速度增加而增加;传播时间20 μs~30 μs期间为第二阶段,在此阶段超声波完全透过孔洞,各孔洞尺寸模型出现第一次声压极大值峰值时间点在28 μs左右。出现该现象是因为当超声波透过孔洞到达孔洞下边界时,由于介质的变化导致孔洞下边界上质点振动速度增大进而声压增大。进一步分析发现声压极大值峰值时间点以及大小都与孔洞尺寸呈现正相关性,原因是孔洞尺寸越大导致超声波到达孔洞上边界的传播时间越短,相应的边界质点振动时间提前,出现峰值时间越早峰值点的值也越大;传播时间30 μs之后为第三阶段,在此期间声压极大值出现一次增加后再减少,原因是声波在到达接收边界上时,导致边界上受振动质子的速度和个数增加而后声波逐渐被接收边界吸收。
2.2 孔洞角度对超声波传播特性的影响
为了探究孔洞角度与超声波传播特性之间的关系,选取了0°,30°,45°,60°,90°和完整(无孔洞)模型透射边界上声压波幅大小进行对比分析。由图6可知,模型超声波透射幅值与孔洞角度的变化呈现负相关性。完整模型的声压波幅最大为384 Pa,而0°模型较完整模型波幅下降了10.7%,为343 Pa,当模型孔洞角度为90°时,较完整模型波幅下降了44.5%,为213 Pa。原因是孔洞角度决定着声波垂直向孔洞传播方向面积的投影,即孔洞角度增大时投影面积增大,造成对声波透射干扰增强,声波传播过程中的能量损失增大。
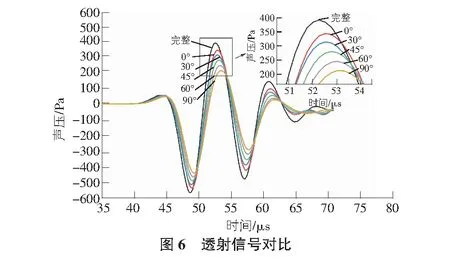
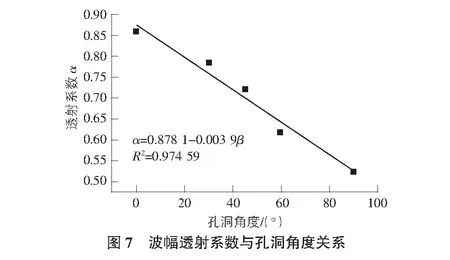
图7为5种不同孔洞角度与波幅透射系数的关系,分析发现孔洞角度与透射系数存在线性关系,拟合相关系数R2为0.97,这进一步说明随着孔洞角度增加即垂直声波传播方向投影面积增大,声波在模型传播过程中能量衰减越大,导致波幅透射系数降低,超声波在孔洞模型中透射能力越弱。
由于超声波在介质传播过程中缺陷(孔洞、裂缝等)会对声波声场传播产生一定的干扰,如图8所示,选取了孔洞角度为45°条件下超声波传播过程中声压分布情况。分析发现随着声波在孔洞模型中传播声压值和分布出现了明显差异。在声波从入射边界进入但并未完全透过孔洞0 μs~20 μs期间,声波沿直线传播没有出现干扰现象;当声波传播穿过孔洞20 μs~30 μs期间,由于传播介质的改变干扰了声波的传播,此阶段声波出现明显的反射现象;声波传播到被透射边界完全吸收的30 μs~40 μs期间,此阶段声波出现明显的散射和绕射现象,直至声波传播到透射边界后被完全吸收,至此结束了超声波的传播过程。

为了深入探究不同孔洞角度下超声波传播过程中声压大小时变规律,如图9所示提取了传播全过程中声压极大值与时间关系曲线进行分析。
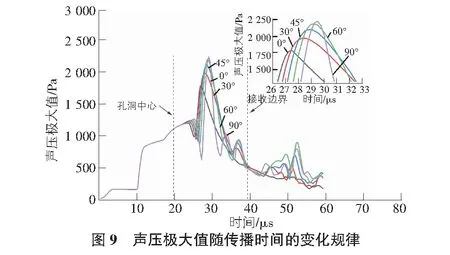
可知在声压极大值方面,不同孔洞角度对超声波传播的响应主要有两方面:
1)声压极大值出现多峰值。当声波从入射边界传播到孔洞边界之前时,各孔洞模型声压极大值均随时间等值增大;当声波透过边界进入孔洞29 μs左右时,由于声波传播到孔洞边界导致边界上受振动质点的数量和速度增大,各孔洞模型相继出现第一次也是全部传播时间段内最大声压极大值峰值点;当声波透出孔洞到最后被模型底部完美匹配层吸收时,声压极大值出现二次峰值点,但声压值总体趋势呈递减趋势发展。
2)各孔洞模型中出现声压极大值峰值大小与时间点和孔洞角度相关联。如图9所示,当各模型出现第一次也是最大一次声压极大值峰值点时,孔洞模型角度越大出现声压极大值越大,而相应的时间点越晚,比如孔洞角度为0°,45°,90°时,出现峰值点的大小和时间分别为27.1 μs和1 785 Pa,28.9 μs和2 093 Pa,29.7 μs和2 234 Pa。
2.3 孔洞形状对超声波传播特性的影响
为了探究孔洞形状对超声波传播特性的影响,如图10所示,选取了5种不同形状孔洞模型中超声波声压透射信号进行分析,发现单从孔洞形状方面分析声波波幅信号没有明显的规律性。而从孔洞垂直声波传播方向的尺寸分析发现,垂直声波传播方向尺寸分别为5 mm,10 mm,20 mm的长方形A、正方形、等边三角形B模型中声压波幅为364 Pa,291 Pa,233 Pa。说明当模型孔隙率相同但孔洞形状不同时,孔洞垂直声波传播方向的尺寸是影响波幅大小的关键,即孔洞垂直声波传播方向的尺寸越大,声波波幅越小。

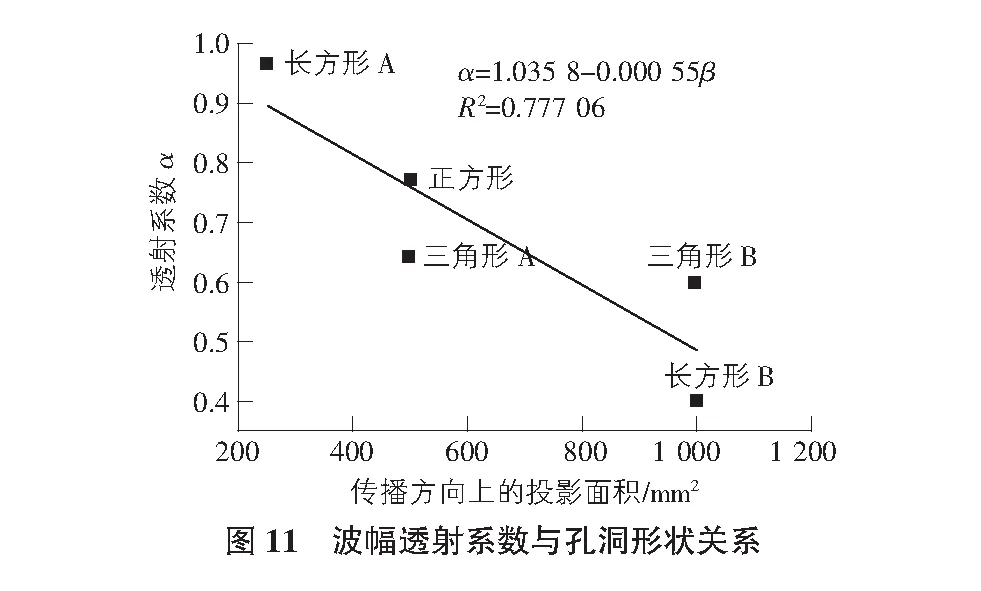
基于孔洞形状与波幅信号没有明显的规律性,而与垂直声波传播方向的孔洞尺寸存在明显的负相关,因此提取图11波幅透射系数与孔洞垂直声波传播方向上投影面积关系深入分析。利用线性拟合的方法将五种不同孔洞形状垂直声波传播方向的投影面积与透射系数进行分析,线性拟合系数R2为0.777拟合效果一般,但这也在一定程度上反映了在孔隙率相同而孔洞形状不同条件下,孔洞垂直声波传播方向的投影面积越大,波幅透射系数越小,声波透射能力越弱。
为了深入探究超声波传播过程中声场分布与孔洞形状之间的关系,如图12所示,分别选取了正方形和三角形A两种典型声波传播过程中的声压快照图进行研究。由图12发现,声波传播到孔洞尺寸、边界、棱角都会出现声压场紊乱的现象,说明声波传播受到了孔洞干扰,但孔洞形状对声压场干扰的形式不同。如正方形孔洞(如图12(a)所示)超声波在孔洞上边界主要发生反射现象,而绕射现象主要发生在孔洞左右边界。而三角形A孔洞(如图12(b)所示)在声场中主要发生散射和绕射现象。

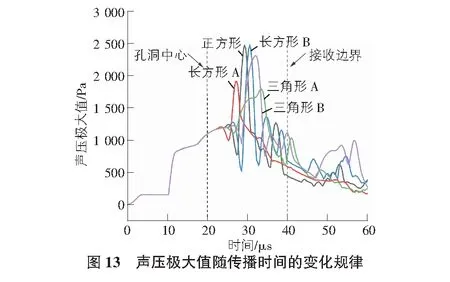
基于不同孔洞形状会导致模型中超声波声压场出现不同的紊乱现象,为了探究不同孔洞形状中声波传播过程中声压极大值与孔洞形状的变化关系,选取了如图13所示五种不同孔洞形状声压极大值时间曲线图。发现不同孔洞形状声压极大值出现明显的多峰值现象,但出现声压极大值峰值时间点和大小与孔洞形状没有明显的关系,而在孔隙率、透射下边界尺寸相同的不同孔洞形状模型中,出现声波声压极大值最大峰值点的大小和时间与孔洞平行声波传播方向的尺寸呈负相关,即孔洞平行声波传播方向的尺寸越大,声压极大值最大峰值点的值越小,相应出现峰值点的时间点越晚。如图13所示,正方形孔洞和三角形A孔洞模型孔隙率、透射下边界尺寸相同,出现声压极大值最大峰值点的时间和大小分别是29.1 μs和2 417 Pa,33.4 μs和1 814 Pa,在相同条件下长方形B和三角形B模型中出现声压极大值最大峰值点的时间和大小分别是30.3 μs和2 421 Pa,31.9 μs和2 293 Pa。所以在孔隙率、透射下边界尺寸相同的不同孔洞形状模型中,平行声波传播方向的尺寸是造成出现声压极大值最大峰值点的时间和大小存在规律性差异的关键,也从侧面反映了孔洞形状会造成超声波在传播过程中存在差异。
3 结论
为了探究含孔洞岩样中超声波传播特性规律,采用COMSOL建立了不同孔洞尺寸、角度、形状三维孔洞模型,利用压力声学模块进行求解计算,从声压透射信号、波幅透射系数、声压快照图、声压极大值四个声学参数方面分别探究了不同孔洞模型超声波传播特性规律。主要结论有如下几点:1)从声压透射信号、波幅透射系数、声压快照图、声压极大值四个声学参数与不同孔洞模型整体分析得到,三种孔洞模型对超声波传播影响关系为孔洞尺寸>孔洞角度>孔洞形状。2)超声波在三种孔洞模型传播中,超声波透射信号和波幅透射系数与垂直于声波传播方向孔洞尺寸或面积存在负相关性,说明垂直于声波传播方向孔洞尺寸或面积是造成声波能量衰减的主要原因。因此,从超声波透射信号和波幅透射系数方面可以定量的评价地下岩土体孔洞的大小。3)岩体存在缺陷时,超声波在传播过程中会产生反射、绕射、散射影响,导致声压场出现不同程度的紊乱现象。在孔洞尺寸方面,声压极大值峰值时间点和峰值大小与孔洞尺寸呈正相关;孔洞角度方面,声压极大值峰值时间点与孔洞角度呈负相关,与峰值大小呈正相关;在孔洞形状方面,声压极大值最大峰值时间点和峰值大小与孔洞平行声波传播方向的尺寸呈正相关。因此,分析声压极大值最大峰值时间点和峰值大小关系可以定性的评价地下岩体孔洞形态。
