复合材料电杆结构参数优化研究★
2022-08-12郑春生杨岚琦刘彦君安利强江文强
郑春生,李 想,杨岚琦,王 哲,刘彦君,安利强,江文强
(1.胜利石油管理局有限公司电力分公司,山东 东营 257000; 2.华北电力大学机械工程系,河北 保定 071003)
1 概述
纤维增强树脂基复合材料具有轻质高强、耐腐蚀、耐疲劳、电绝缘等特点,是输电杆塔结构材料的理想选择[1]。
复合材料电杆强度高、重量轻,其重量仅为200 kg,是普通水泥电杆的1/6,而且弯曲强度可达水泥杆的3倍以上,可有效提高安装效率,降低劳动强度。同时,复合材料杆塔应用于输电线路中,可有效降低塔基的电磁场强度,减少线路维护量,节省线路走廓投资及安装成本[2]。但目前复合材料电杆的整体刚度较小且风摆幅度大,易对线路的正常运行造成不利影响[3]。加拿大RS公司研制的组合套接结构式输电杆,创新性地采用了聚氨酯树脂体系,与常规的不饱和聚酯树脂复合材料相比,具有更大的强度、耐冲击力以及较大的比强度[4]。Urgessa等[5]研究发现杆塔的最大应力随着缠绕角的增加先增大后减小。Haijun Xing[6]进行了220 kV输电线路杆塔复合绝缘交叉臂压杆承载力计算研究。周邢银等[7]将复合材料叶片简化为对称非均匀层合板梁,结合有限元与静态位移测量方法,分析得出中心耦合区域获得的弯扭耦合效应显著。张颖等[8]对不同位置偏轴对称铺设的复合材料层合板进行静力和模态分析,得出在低阶模态时中部区域耦合板耦合效果明显,端部耦合板在高阶模态时弯扭耦合效果更明显。
基于上述研究,本文以电杆复合材料化、轻质高强为目的,利用仿真分析的手段,研究复合材料电杆结构特性以及结构增强的方法,对其进行结构参数优化,从而有效提高复合材料电杆的弹性模量,增加电杆刚度和其承载力。
2 复合电杆材料选型与建模
2.1 复合电杆的材料选型
复合材料型材主要包括以下几种[9]:
1)非受力构件型材,该类复合型材通过拉挤玻璃纤维与不饱和聚酯树脂成型[10],其力学性能较差。
2)环氧/玻璃纤维型材,该类型材采用玻璃纤维与环氧树脂为原材料,经过预浸纤维缠绕成型[11],其弯曲模量和压缩强度均较低,继而限制了作为杆塔材料的使用。
3)增强型环氧/玻璃纤维型材,这种型材不但将增强的玻璃纤维作为受力材料,而且使用复合剂,添加了抗老化成分[12],其成本相比其他型材较昂贵。
4)环氧/E-玻璃纤维型材[13],该类型材由E-玻璃纤维与环氧树脂两者通过拉挤-缠绕工艺成型,其强度和模量均优于其他类型材复合材料电杆通常采用环氧/E-玻璃纤维型材。
2.2 有限元模型建立
如图1所示为复合材料电杆的外形尺寸,其结构参数如表1所示。其中,L为杆长;L1为横担高度;L2为埋深;L3为稍端至荷载点距离;D为直径或根径;d为稍径;δ为壁厚;δ1为稍部壁厚;δ2为端部壁厚;电杆锥度为1∶75。本文利用ABAQUS建立电杆的三维实体模型,采用Lamina材料模型,其参数设置如表2所示。在计算极限承载力时,分别采用最大应力准则、蔡吴准则、蔡希尔准则进行损伤判定。

表2 纤维材料参数
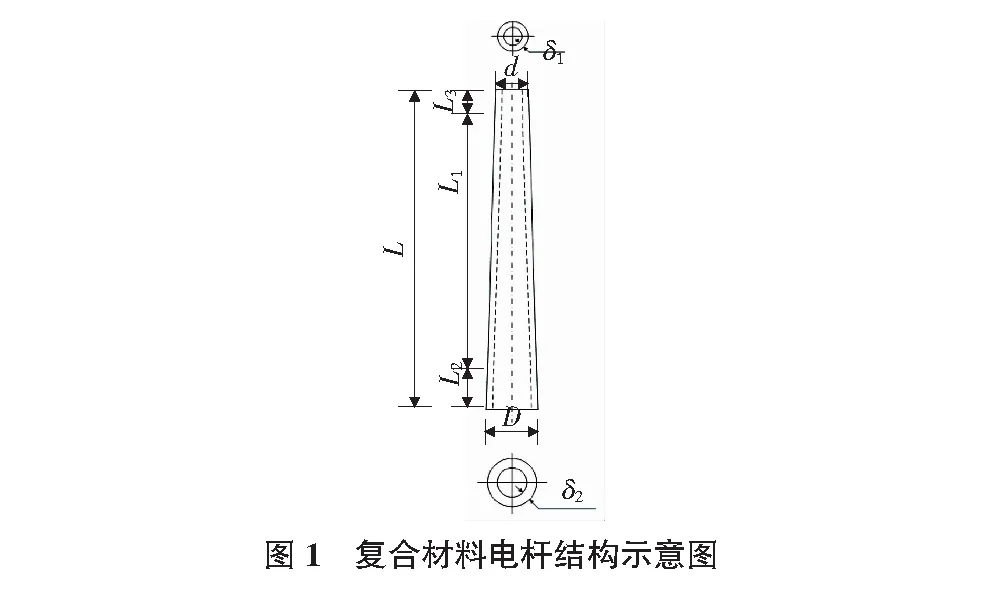

表1 复合材料电杆结构尺寸
2.3 杆塔铺层及约束加载
本文以沿电杆轴向方向为纤维0°方向并以此作基准完成对铺层角度设置。根据复合材料电杆的实际情况,设电杆铺层数目为11层,Ply1,Ply4,Ply7,Ply10纤维角度为α,Ply2,Ply5,Ply8,Ply11纤维角度为-α,Ply3,Ply6,Ply9纤维角度为β,模型铺层方案定义[α,β]11。
如图2所示为铺层堆叠情况。为了研究复合材料电杆在大风工况下的极限承载力,在有限元模型电杆底面施加沿电杆轴向位移约束,并在电杆埋深一半处,其切分平面上施加该平面位移约束。
对杆塔进行受力分析,可将电杆、横担、导线等所受的风压简化为距电杆顶端L3处的等效载荷Feq的作用,其计算公式如下:
(1)
其中,FD为导线风压;FT1,FT2分别为电杆横担以上、以下部分所受风压;G为导线及绝缘子重力。如表3所示为不同风速条件下计算得到电杆风载荷,将其代入式(1)可计算出在不同风压下杆塔等效载荷Feq。
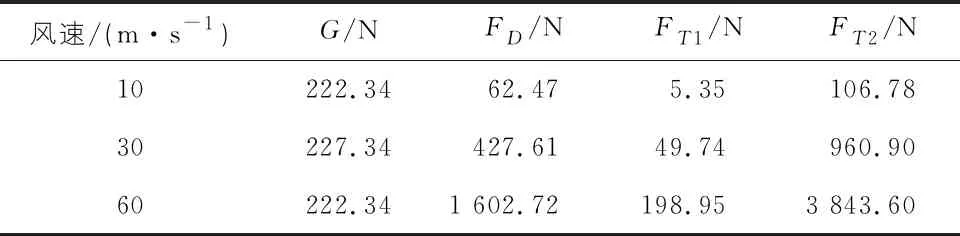
表3 载荷值
3 复合材料电杆结构参数优化
3.1 铺层纤维角度对刚度的影响
按照前文铺层角度定义,改变铺层角度建立如表4所示9种分析模型,并对比各模型在极限工作风速30 m/s的风载荷作用下,电杆的变形及顶端位移值。首先在碳质量分数为0%、纤维铺层数目为11层的情况下,研究材料纤维铺层角度对电杆刚度及承载力的影响。
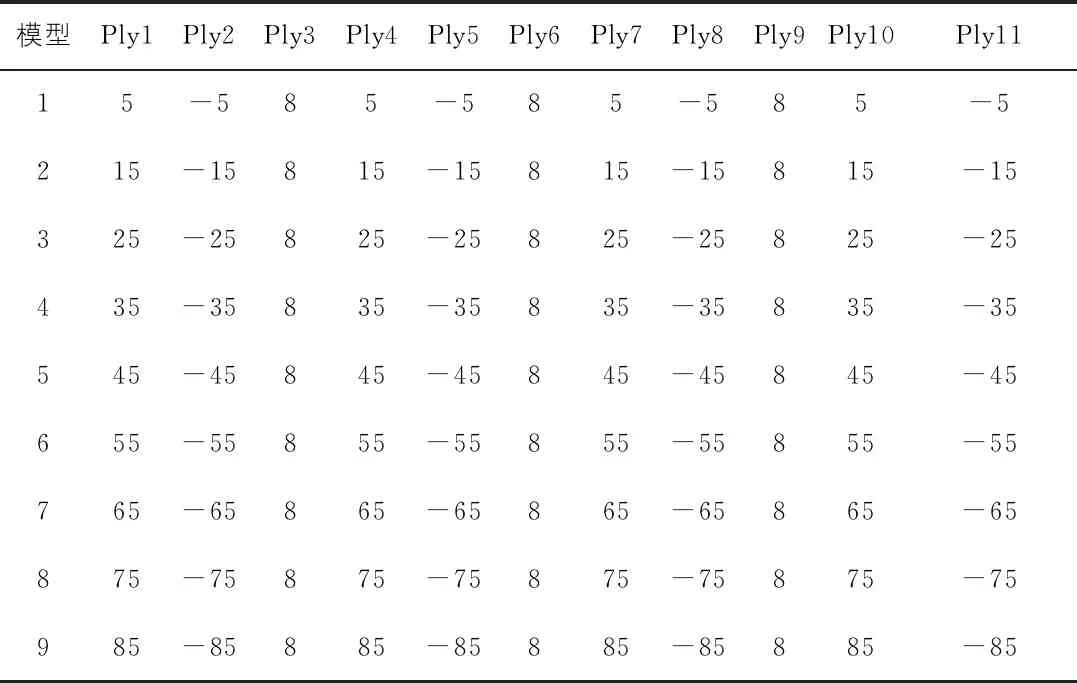
表4 不同纤维铺层角度模型 (°)
定义各模型电杆最大位移值为Umax,电杆极限承载力为Flimit,则位移增幅λ与极限承载力增幅β可分别按式(2),式(3)计算。
λ=(Umax,i-Umax,75)/Umax,75
(2)
β=(Flimit-F0)/F0
(3)
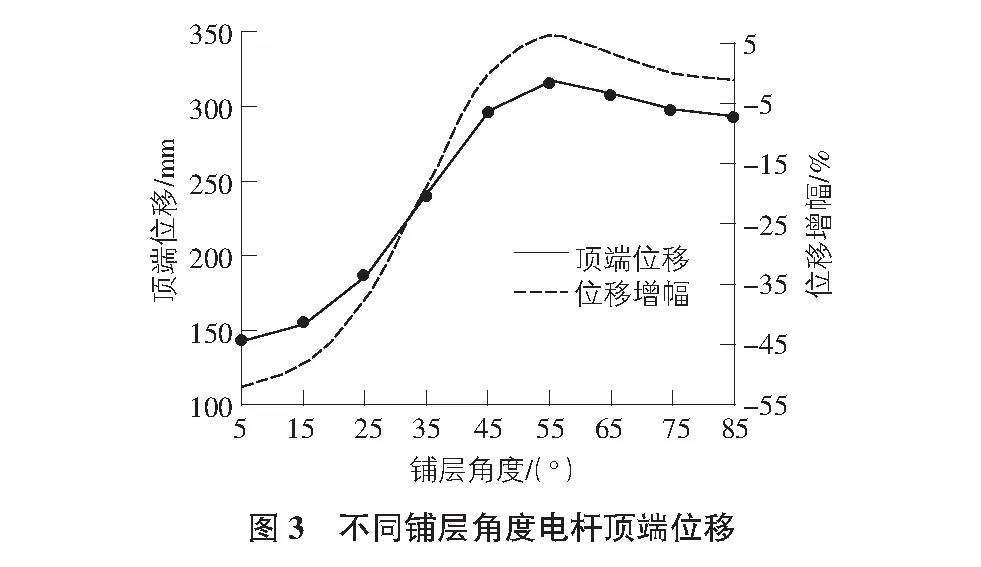
其中,F0为[75°,8°]11铺层的极限承载力。整理电杆最大位移值Umax及位移增幅λ如图3所示。
从图3可以看出,由于材料各向异性,在受力过程中,铺层角度与位移关系并非单调曲线。现有铺层方案为[75°,8°]11,当α在45°~85°之间时,顶端位移变化缓慢,且在55°时达到了最大值,α<45°时,顶端位移随α增加而减小。当α由75°减小至35°时,刚度提高约18.9%;当α从35°减小至25°时,刚度提高约18.6%;当α从25°减小至15°时,刚度提高约10.6%,当α从15°减小至5°时,刚度提高约3.8%。由此可见,改变纤维铺层角度能够有效提高结构刚度,且考虑到采用缠绕铺层工艺的可行性,建议α取值范围为25°~35°,此时刚度可提高约18%~37%。
3.2 铺层纤维角度对极限承载力影响
在等效作用点上施加沿电杆横向位移载荷,提取该点处横向位移及支反力,得到电杆的载荷-位移曲线如图4所示。图中拐点位置对应复合材料电杆的极限承载力,提取此刻该作用点处支反力值Flimit如表5所示,整理极限承载力变化幅度β如图5所示。

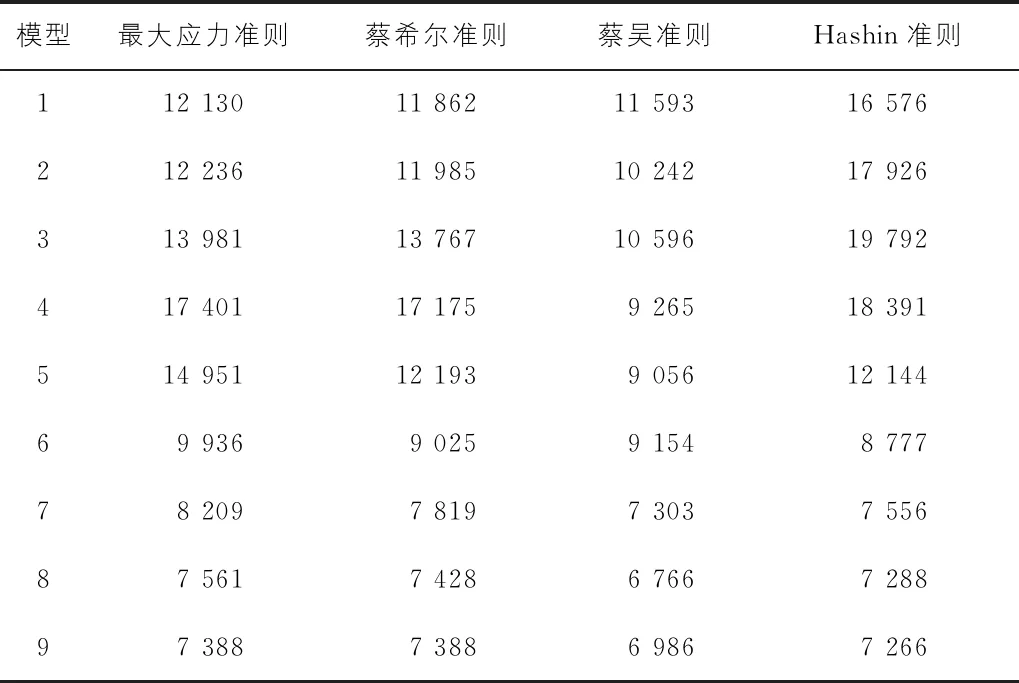
表5 不同铺层角度电杆极限承载力Flimit N
现有铺层方案α为75°,当α在45°~85°之间时,极限承载力几乎不变,仅在55°时有相对较大幅度的提高,此时极限承载力提高约为25%;α由45°减小至30°时,极限承载力随α减小而增大,当α=35°时,极限承载力到达峰值,在不同判定准则下极限承载力最大可提高152%,最小提高37%,当α由35°减小至5°时,在某些判定准则下极限承载力增幅略有降低,但相对现有铺层方案极限承载力仍可提高51%~171%。
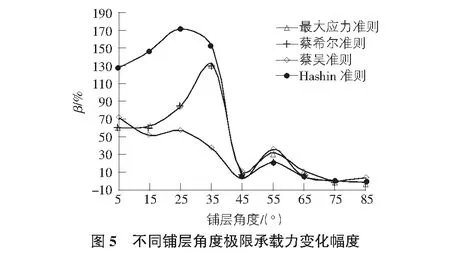
结合角度对刚度的影响,并考虑实际铺层操作的可行性,建议取值范围为25°~35°,此时极限承载力可提高至少30%。
3.3 铺层数目对刚度的影响
结合铺层角度的影响,采用碳质量分数为0%、纤维铺层角度为[35°,8°]11的方案,研究铺层数目对电杆刚度及承载力的影响。通过改变铺层数目建立如表6所示3种不同铺层数目分析模型。
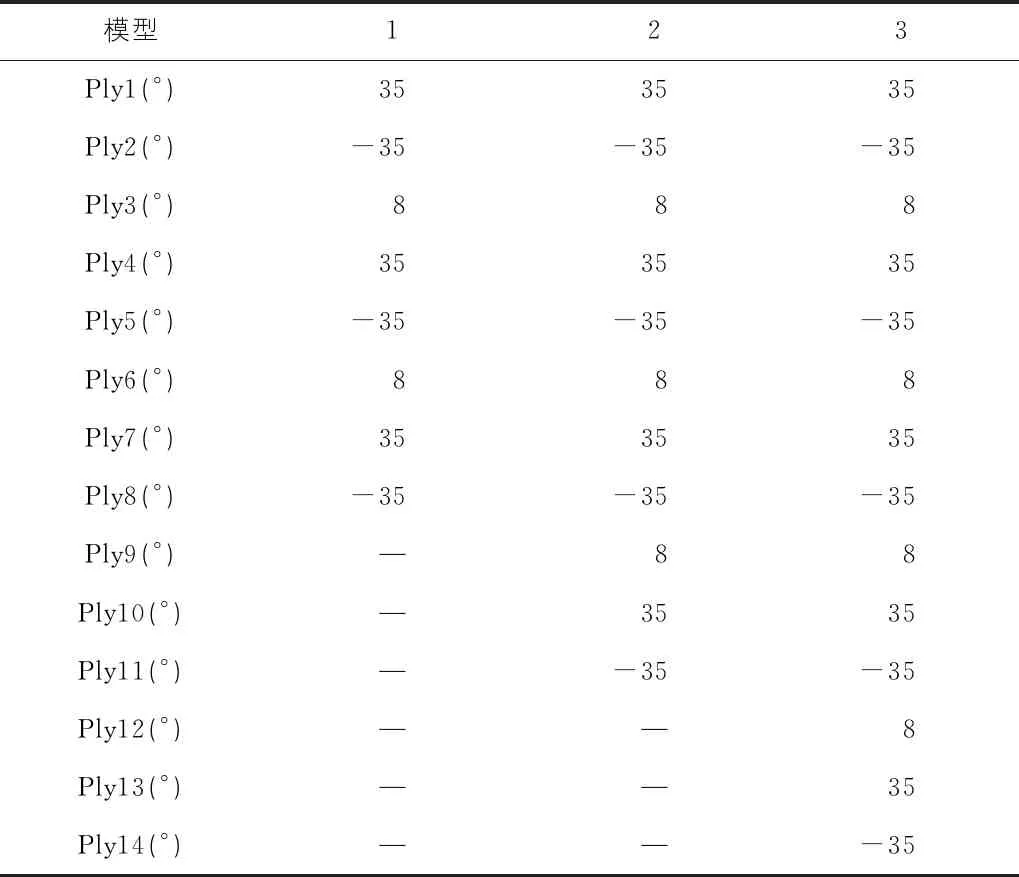
表6 不同铺层数目模型
对比表中模型在极限工作风速30 m/s的风载荷作用下电杆的变形及顶端位移值。整理顶端位移与位移增幅曲线如图6所示。现有铺层数目为11层,当铺层数目减小3层后,电杆刚度降低约48%,当铺层数目增加3层后,电杆刚度提高约25%,变化幅度有所降低,采用线性插值的方法,得到当铺层数目为12层,13层时,电杆刚度可分别提高约10%,18%。
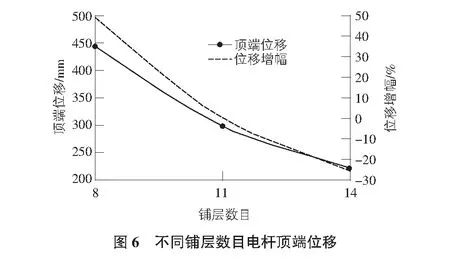
施加相同载荷时,电杆顶端位移减小,说明增加铺层数目能够有效提高结构刚度,当铺层数目分别增加1层、2层、3层时,电杆刚度相应的提高10%,18%,25%。增加铺层数目并考虑结构尺寸,建议铺层取值范围为12~14,刚度可提高约20%。
3.4 铺层数目对极限承载力的影响
按前文所述施加载荷,得到满足各损伤判定准则时极限承载力值Flimit如表7所示。在各损伤准则判定下,增加铺层数目均会使电杆极限承载力提高。整理极限承载力变化幅度β如图7所示。

表7 不同铺层数目电杆极限承载力 N
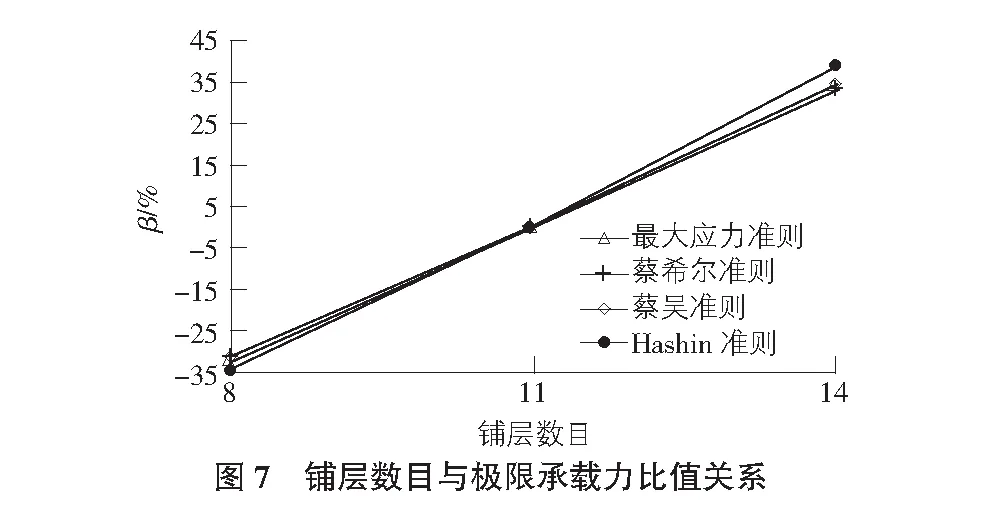
从表7可以看出,随着铺层数目增加,在不同损伤准则判定下,结构整体极限承载力均近似呈线性增加,铺层数目减少3层时,极限承载力降低约34%,铺层数目增加3层时,极限承载力提高约38%。采用线性插值的方法,当铺层数目为12层、13层时,极限承载力分别提高10%,25%。结合实际结构尺寸,以及铺层数目对刚度的影响,综合建议铺层取值范围为12层~14层,极限承载力可提高约25%。
3.5 含碳百分数对刚度的影响
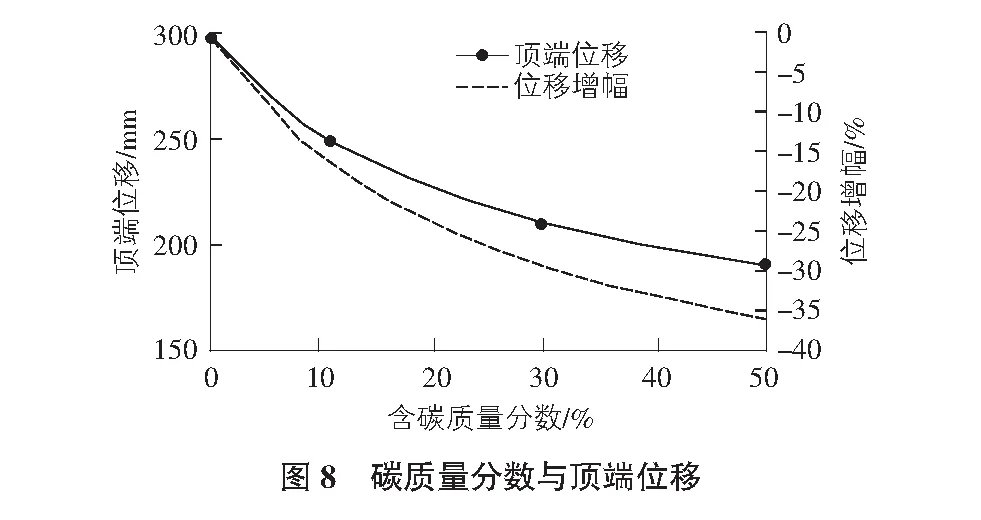
最后结合以上两个参数的影响,采用纤维铺层角度为[35°,8°]11、铺层数目为14层的方案,研究含碳百分数对刚度及承载力的影响。如表8所示为不同含碳质量分数的4种分析模型,对比表中模型在极限工作风速30 m/s载荷作用下电杆的变形及顶端位移值。整理电杆最大位移值Umax及位移增幅λ如图8所示曲线。

表8 纤维8°铺层不同碳质量分数模型
现有铺层材料碳质量分数为0%,改变纤维方向为8°的铺层纤维材料中碳质量分数,将含碳质量分数增加11%时,电杆刚度提高约16.4%,含碳质量分数由11%增加至30%,电杆刚度提高约13%,含碳质量分数由30%增加至50%时,电杆刚度提高约6%。随着含碳质量分数的增加,电杆刚度也逐步增加,但增加幅度逐渐降低。施加相同载荷时,电杆顶端位移减小,说明增加含碳百分数能够有效提高结构刚度,若考虑提高结构刚度,建议增加含碳质量分数至10%,电杆刚度可提高16%。
3.6 含碳百分数对极限承载力的影响
与前文所述施加载荷方法相同,得到满足各损伤判定准则时极限承载力值Flimit如表9所示。在各损伤准则判定下,增加碳质量百分数均会使电杆极限承载力提高。整理极限承载力变化幅度β值如图9所示。

表9 不同含碳质量分数电杆极限承载力Flimit N
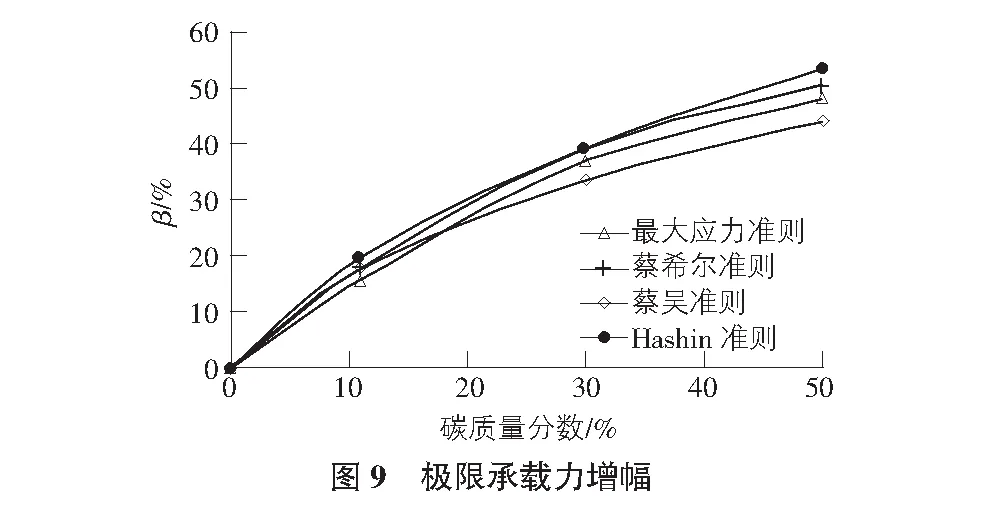
从图9可以看出,在不同损伤准则判定下,随着含碳质量分数的增加,结构极限承载力均增加,当碳质量分数为11%,30%,50%时,极限承载力分别提高约17%,36%,48%,在现有曲线上插值得到碳质量分数为20%,40%时,极限承载力分别提高约28%,42%,故碳质量分数由0%且以10%增加的幅度增加到50%时,得到结构极限承载力相应的增加幅度分别约为17%,11%,8%,6%,6%,可以发现碳质量分数在0%~10%时,极限承载力增幅最大。
结合碳质量分数对顶端位移的影响,当碳质量分数增加时,刚度与极限承载力均会增加。但如果一味地增加含碳的质量分数追求较高的刚度与承载力,则可能用较高的成本来换取刚度与承载能力微小的增长。因此增加纤维含碳量并考虑成本影响,综合建议加入碳质量分数为10%,此时刚度可提高约16%,极限承载力可提高约17%。
4 结语
本文利用Abaqus有限元,分析了不同风速下复合材料杆塔的承载力,通过分析铺层角度,铺层数目,含碳质量分数等参数对杆塔的承载力以及刚度的影响规律,给出了最合理的各项参数,从而使杆塔拥有更优的力学性能。
1)改变纤维铺层角度在一定范围内可以提高结构刚度和极限承载能力,建议α取值范围为25°~35°,刚度可提高18%~37%,极限承载力可提高至少30%。
2)铺层数目减少,刚度与极限承载力均降低,故不建议减小现有铺层数目。增加铺层数目并考虑结构尺寸,综合建议铺层取值范围为12~14,刚度可提高约20%,极限承载力可提高约25%。
3)碳质量分数增加,刚度与极限承载力均增加,建议加入碳质量分数为10%,刚度可提高约16%,极限承载力可提高约17%。
