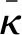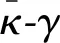基于移动荷载傅里叶谱的桥梁共振频域分析
2022-08-09李锦华张焕涛陈水生刘全民
李锦华,张焕涛,陈水生,刘全民
(华东交通大学 土木建筑学院,江西 南昌 330013)
列车速度是高速铁路技术水平的最主要标志,然而,列车速度的不断提升不仅会加剧桥梁动力响应,还会减少铁路桥梁寿命。在高速列车作用下,铁路桥梁除了避免产生过大的变形,还需要满足乘客舒适度要求。因此,列车荷载作用下高速铁路桥梁的共振响应研究至关重要[1-2]。
移动荷载与车-桥耦合是研究列车作用下桥梁共振响应的两类模型[3]。对于列车激励下桥梁共振问题的研究,可通过车-桥耦合模型的数值模拟进行,如桥梁跨径、荷载速度、间距和荷载数量等参数的影响分析[4-6]。苏木标等[5]采用车-桥耦合模型,发现桥梁共振的发生和发展受到许多参数的影响,如桥梁的跨度、刚度和阻尼,以及车辆的长度、悬挂弹簧刚度等参数。黄文杰等[6]基于列车-轨道-桥梁系统有限元分析,分析了桥梁结构参数对桥梁共振的影响,发现桥梁质量、刚度、阻尼比等参数变化将会对桥梁共振产生重要影响。与移动荷载模型相比,车-桥耦合模型计算得到的桥梁振动响应计算结果往往偏小[7-8]。因此,对桥梁振动响应研究时,可以采用移动荷载模型来模拟列车对桥梁的激励荷载。吕龙等[9]采用移动荷载模型研究了斜拉桥的纵向共振机理,推导了纵向共振速度。高传伟等[10]通过移动荷载模型对轨道交通桥梁进行了共振和消振响应的研究。文献[11-14]首先根据发生机理的不同对桥梁共振进行了分类,然后分别进行单个移动荷载、等间距移动荷载、非等间距移动荷载作用下的桥梁共振与消振响应研究,并在时域内,理论推导了引起桥梁发生共振及消振的移动荷载速度。张铎等[15]将等间距列车荷载简化为简谐移动荷载,分析了移动荷载的谐振频率、速度等参数对桥梁发生共振响应的影响。而实际上,以共振速度行驶的移动荷载,有时并不能使得桥梁自由振动时期产生最大位移响应。对于单个移动荷载从低速到高速匀速通过桥梁后,会使得桥梁振动响应产生一系列极值点,其所对应的移动荷载速度并不是共振速度[11,16-17]。移动列车荷载激励下的桥梁振动响应主要是在时域内进行研究,其相关理论推导过于复杂,且不同速度的移动荷载所激励的桥梁振动响应需要反复计算求解。相对于时域研究,频域分析直观且无需求解微分方程等有诸多优势。
因此,本文将研究建立多个移动荷载激励下桥梁共振响应的频域分析法,将对移动荷载激励下的桥梁运动方程进行傅里叶变换,进行多个移动荷载激励下的桥梁位移傅里叶谱、移动荷载傅里叶谱的理论推导;然后通过引入两个参数(无量纲速度与间跨比)对移动荷载傅里叶谱进行幅值分析,从而建立移动荷载速度与桥梁最大位移响应之间的关系;最后以简支梁为例来验证理论分析的正确性和移动荷载速度公式的有效性。
1 移动荷载傅里叶谱
移动列车激励下的桥梁如图1所示,桥梁梁体可视为欧拉-伯努利梁,其单位质量为m、结构阻尼为c、弯曲刚度为EI;移动列车可简化为等间距排列的移动荷载模型,即在每节车厢形心处简化为一个集中力P0,且相邻集中力的间距d相等,该间距为整节车厢的长度。因此,对于具有Np节车厢的列车,可简化为Np个集中力Pk(k=1,2,3,…,Np)的移动荷载,总长度Lp=(Np-1)·d,如图1(b)所示。
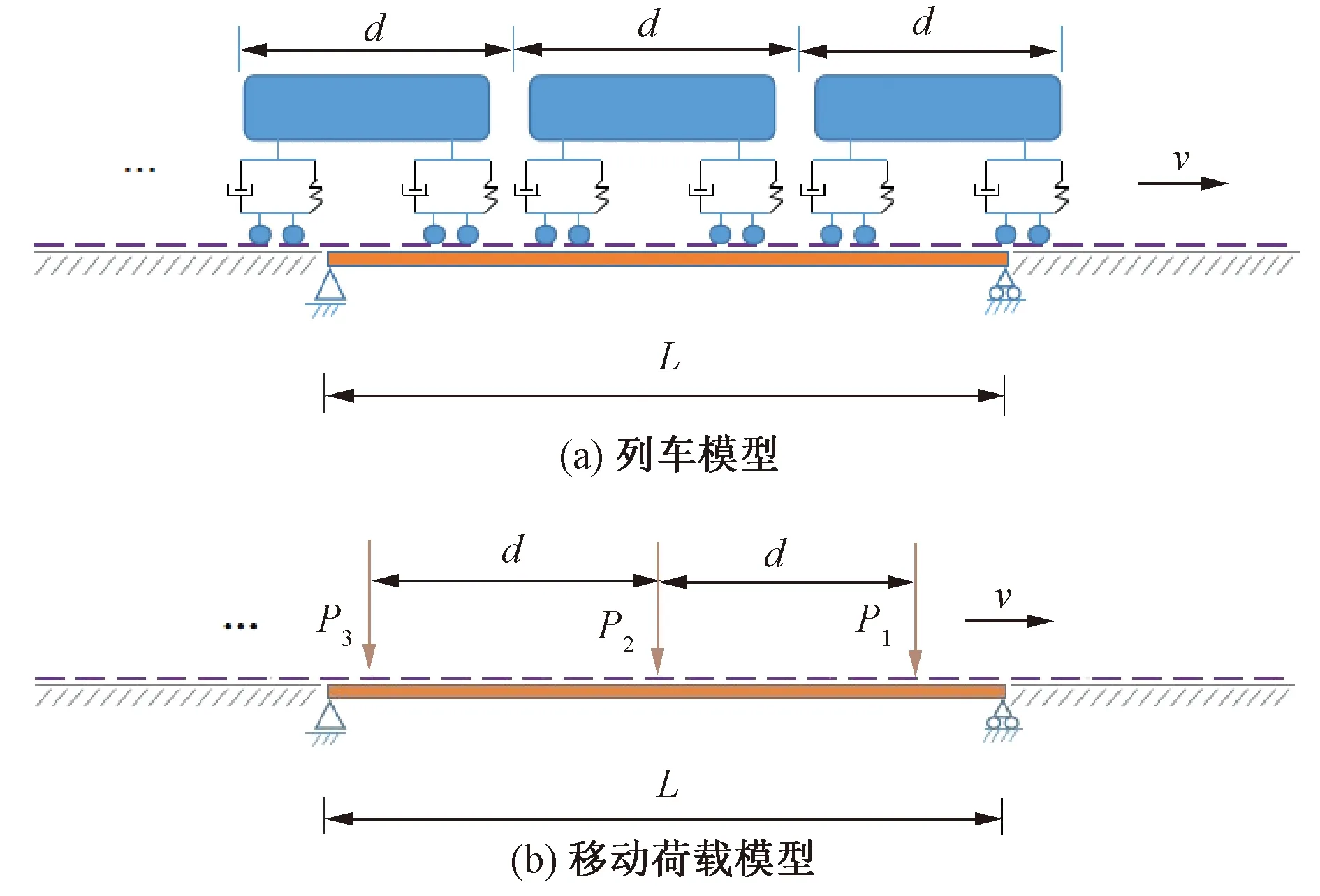
图1 列车及移动荷载模型
对于Np个移动集中荷载Pk(k=1,2,3,…,Np)以速度v匀速通过跨径为L的简支梁桥,在x位置t时刻的桥梁竖向位移y(x,t)满足运动微分方程
(1)
式中:tk为第k个移动集中力上桥的时间;dk为第k个集中荷载与第1个集中荷载的间距;δ为Diarc函数;S(t-tk)=S0(t-tk)-S0(t-tk-L/v)可确定移动荷载是否作用在桥上,其中S0为Heaviside函数。
根据振型叠加法,桥梁竖向位移y(x,t)可表示为
(2)
式中:qn(t)为第n阶广义坐标;φn(x)为桥梁结构的第n阶振型函数。
将式(2)代入式(1),进一步考虑振型正交性,可将桥梁结构运动微分方程分解为n个相互独立的微分方程,即
(3)
式中:ωn、ξn分别为桥梁结构的第n阶圆频率、阻尼比。
简支梁的阵型函数为正弦函数,根据傅里叶变换,运动微分方程式(3)在频域内的解为
Qn(ω)=Hn(ω)Fn(ω)
(4)
式中:Qn(ω)为广义坐标qn(t)的傅里叶变换;ω为圆频率;Hn(ω)为传递函数;Fn(ω)为第n阶振型的移动荷载傅里叶谱。Hn(ω)、Fn(ω)计算式分别为
(5)
(6)
当振型分别为奇数、偶数时,则
(7)
于是,对应的多个移动集中荷载引起的桥梁位移傅里叶谱为
(8)
2 移动荷载激励下的桥梁共振分析
文献[13]研究发现,简支梁桥的振动响应计算仅考虑第一阶竖向振型就可满足精度要求。因此,为了简化分析,仅考虑简支梁第一阶阵型,且不计结构阻尼,对等间距移动荷载引起的桥梁位移傅里叶谱进行取模,可获得简支梁桥位移傅里叶幅值谱,即
|Y1(ω)|=|Q1(ω)·φ1(x)|=|H1(ω)F1(ω)φ1(x)|=
(9)
对于简支梁桥,其结构第一阶振型函数最大值出现在跨中,即当x=0.5L时,φ1(x)出现最大值。而当ω=ω1时(ω1为基频),结构响应传递函数H1(ω)值最大。此时,桥梁位移傅里叶幅值谱(式(9))是否出现最大值,完全取决于移动荷载傅里叶幅值谱|F1(ω1)|的大小。
|F1(ω1)|=
(10)
由式(10)可知,桥梁跨度L、基频ω1、移动荷载间距d及移动荷载个数Np都将会影响|F1(ω1)|的大小。为简化其表达式,引入两个参数,即移动荷载无量纲速度κ=v/ω1L,间跨比(移动荷载间距与桥梁跨度的比值)γ=d/L,则式(10)可进一步表示为
|F1(γ、κ、Np)|=
(11)
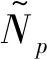
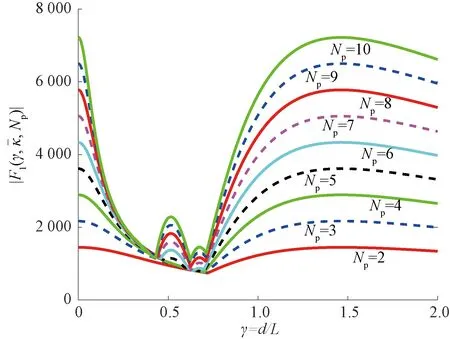
图2 不同移动荷载数对应的曲线
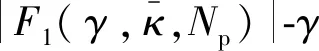
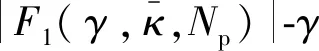
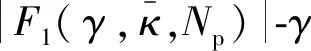
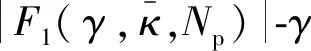
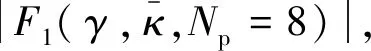
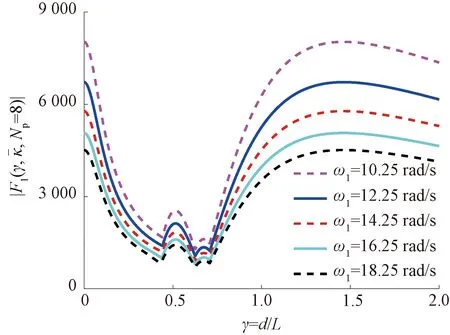
图3 不同桥梁基频下的曲线
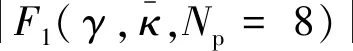
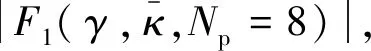
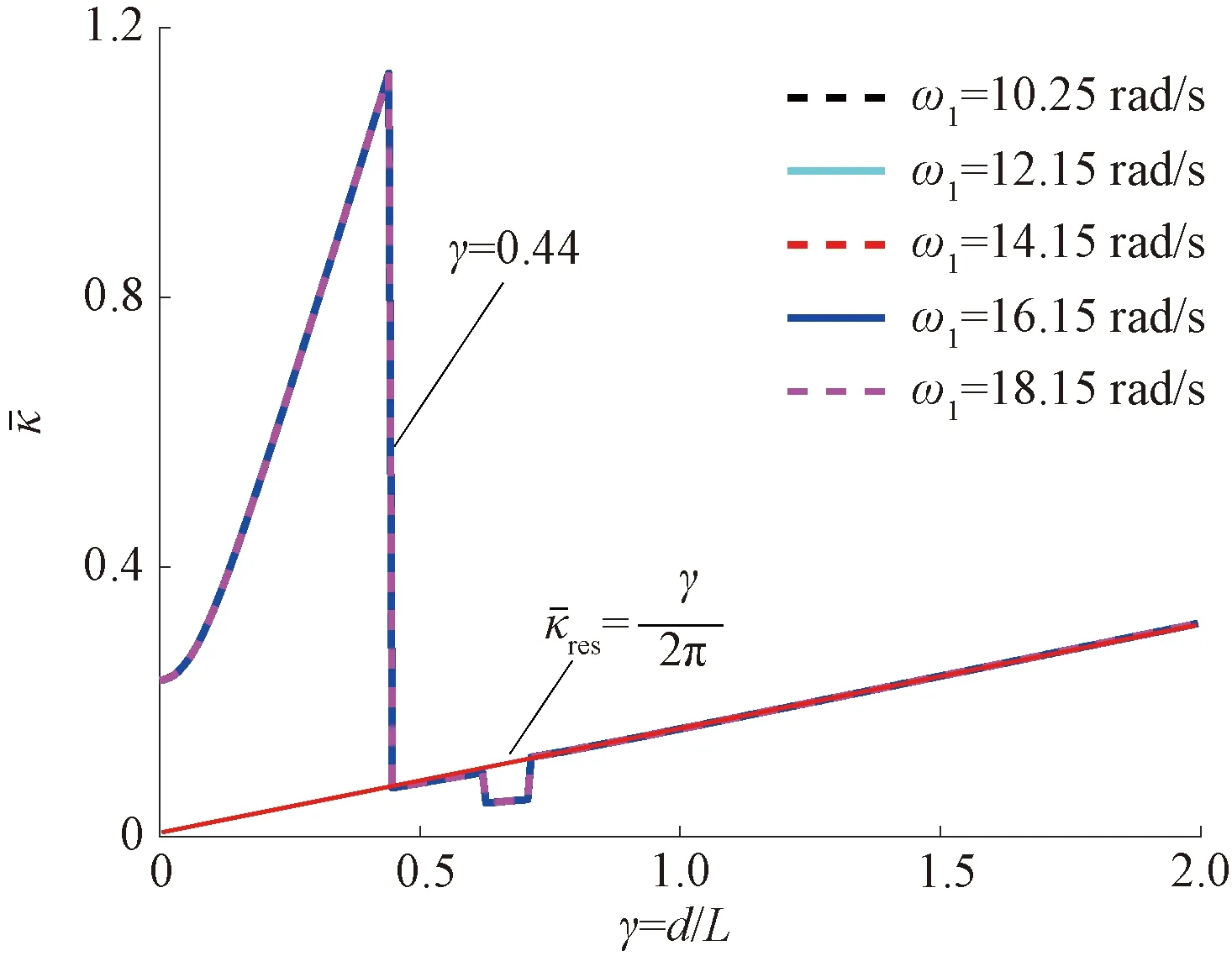
图所对应的曲线
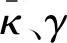
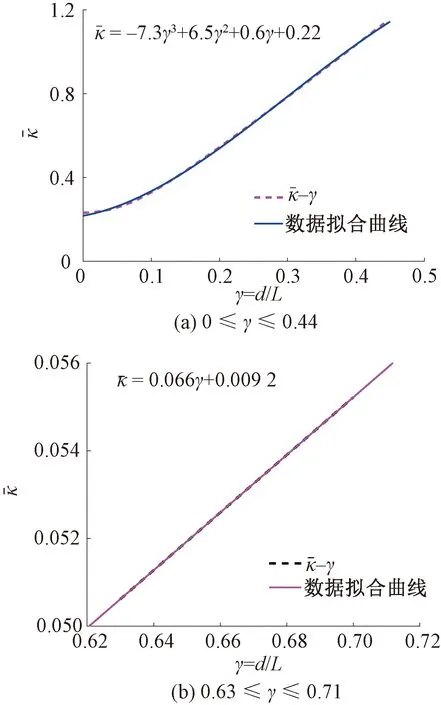
图对应的曲线拟合
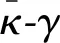
(12)
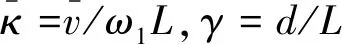
(13)
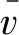
3 算例验证
本文针对在高速铁路中广泛使用的简支桥梁进行研究。仅考虑第一阶模态即可满足简支桥梁的计算精度要求。为简化起见,等距移动荷载作用下简支桥的共振分析中不考虑高阶模态和结构阻尼。因此,为了验证移动荷载作用下桥梁振动响应分析,有必要在时域计算桥梁在移动荷载作用下的振动响应。首先,采用振型叠加法计算一个实例,桥梁和荷载参数如表1所示,即文献[18]在两个移动荷载作用下简支梁的振动响应如图6所示,对于速度为 100 km/h 的简支梁桥在移动荷载作用下,振型叠加法计算的位移响应与文献[18]中的位移响应一致,这表明本文通过振型叠加法计算得到的时域结果的正确性。

表1 桥梁和荷载参数[18]
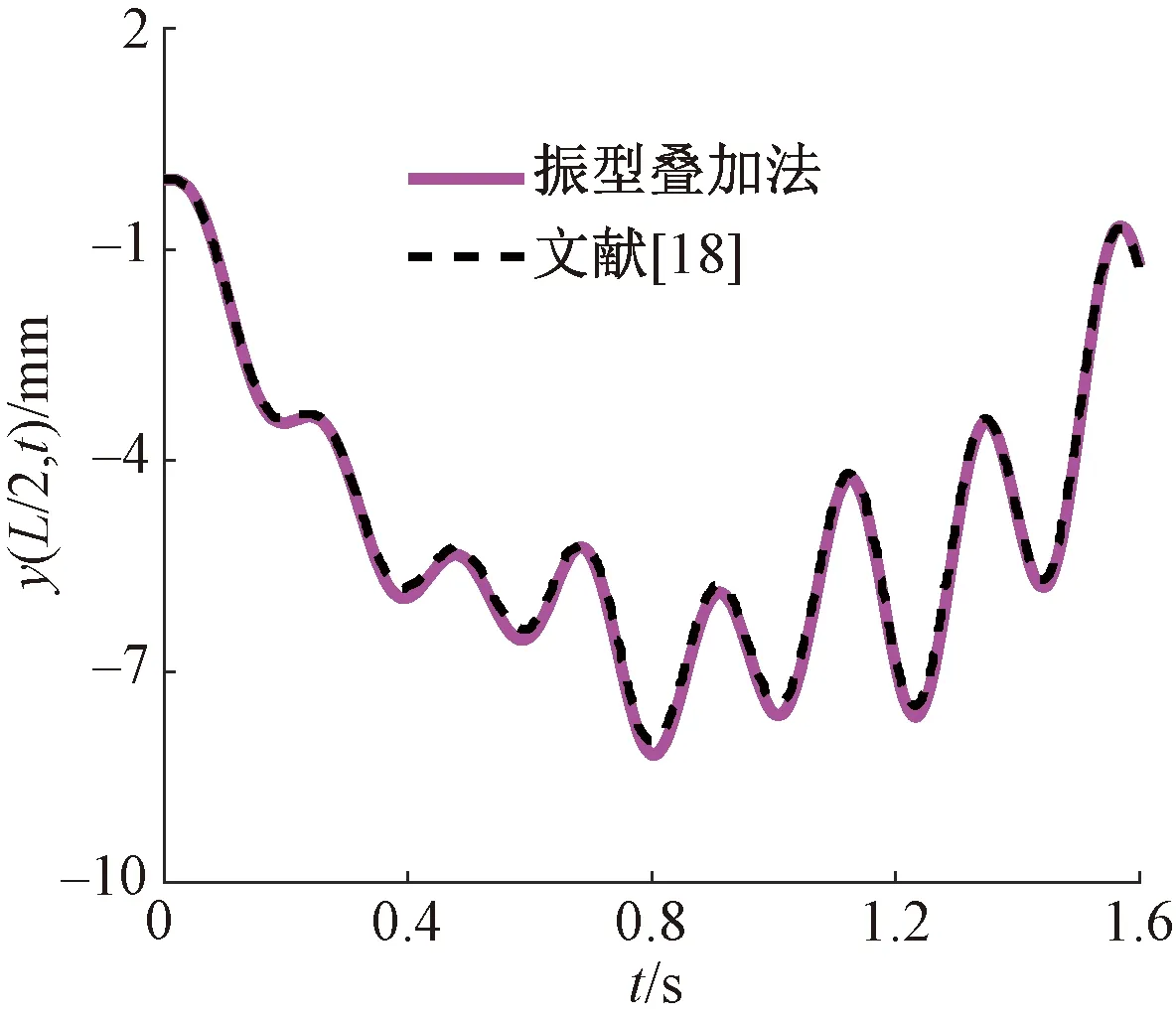
图6 荷载间距为17.5 m时的桥梁跨中竖向位移响应
为了进一步分析桥梁位移傅里叶幅值谱和移动荷载傅里叶幅值谱,通过表1的参数,d=12 m,ω1=29.15 rad/s从频域和时域角度分析不同时速的移动荷载通过桥梁的位移响应。最后得到桥梁的自由振动极值响应、桥梁位移和移动荷载傅里叶幅值谱,如图7所示。由图7可知,当Np=2时,|Y1(ω,v)|中出现了很多极值点,并且随着移动荷载速度v的增加,|Y1(ω,v)|曲线的变化规律与|F1(ω,v)|、|y(L/2,v)|曲线一致。同理,当Np=3时,|Y1(ω,v)|的曲线变化规律与|F1(ω,v)|、|y(L/2,v)|也相同,这说明通过移动荷载傅里叶幅值谱来分析桥梁振动最大位移响应是可行的。
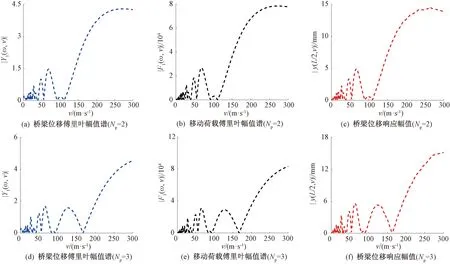
图7 不同移动荷载数下的桥梁位移傅里叶幅值谱、移动荷载傅里叶幅值谱、桥梁位移响应幅值
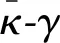
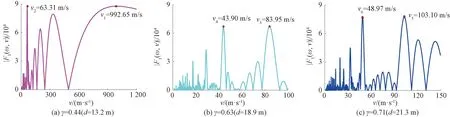
图8 不同间跨比γ的移动荷载傅里叶幅值谱
为了从时域角度验证上述分析计算的正确性,移动荷载分别以图8中移动荷载傅里叶幅值谱最大值对应的荷载速度通过桥梁时,桥梁跨中位置位移时程曲线如图9所示。观察图9(a)可知,移动荷载分别以992.65、63.31 m/s速度通过桥梁时,引起桥梁受迫振动时期的位移最大幅值存在明显差异:
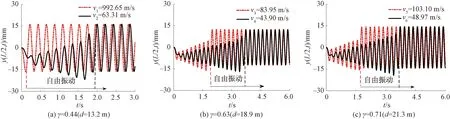
图9 考虑不同间跨比γ的跨中竖向位移时程曲线
max{y(L/2,t)force}v1 为验证式(13)的有效性,桥梁自由振动位移最大幅值响应对应的移动荷载速度与式(13)计算速度如表2所示。经过对比发现,由式(13)所得的移动荷载速度与时域计算所得结果非常接近,误差在5%以内。 表2 桥梁自由振动最大响应对应的移动荷载速度 为分析等距移动荷载作用下简支桥梁的共振,利用傅里叶变换推导了桥梁在移动荷载作用下的位移响应傅里叶谱和移动荷载傅里叶谱。并提出了基于移动荷载傅里叶谱的桥梁共振频域分析方法。最后通过时域分析对实际的桥梁参数进行验证,结论如下: (1)移动荷载傅里叶幅值谱可以有效反映桥梁自由振动的位移幅值。并且移动荷载傅里叶幅值谱随荷载移动速度的变化规律与桥梁位移响应幅值的变化规律是一致的。因此,可以通过移动荷载傅里叶幅值谱的最大值对应的速度来确定导致桥梁位移响应最大值的移动载荷的速度。 由于桥梁自由振动位移响应与荷载数Np有关,因此,本文仅根据实际情况分析了8节车厢作用下的桥梁振动位移响应最大值时的情况,而对于其他移动荷载数Np作用下,桥梁振动位移响应最大值所对应的速度,也可基于该分析方法进行分析求解。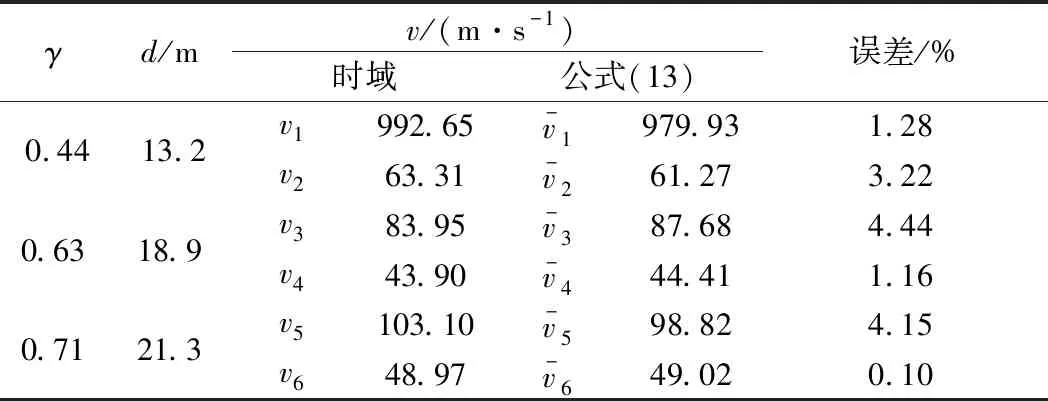
4 结论