德伊高铁地基土变异性分析与概率分布研究
2022-08-09刘先峰张炎飞袁胜洋高泽飞陈伟志
刘先峰,阳 剑,张炎飞,袁胜洋,高泽飞,陈伟志
(1.西南交通大学 土木工程学院,四川 成都 610031;2.西南交通大学 道路与铁道工程教育部重点实验室,四川 成都 610031;3.新疆工程学院 土木工程学院,新疆 乌鲁木齐 830023;4.中铁二院工程集团有限责任公司,四川 成都 610031)
土体参数的不确定性一直以来都是阻碍岩土工程发展的重要问题,一般对土体参数的处理办法是进行数次试验,以试验所得结果的平均值作为土体的基本参数。这种做法明显忽视了土体参数显著的不确定性,用作工程设计和施工时也隐含不可忽视的风险。因此近几十年来考虑土体不确定性的理论逐渐发展,针对土体参数不确定性的研究也开始深入。
Phoon等[1-2]将土体不确定性表述为土体变异性,并指出土体变异性主要来自三个方面:①由自然地质过程产生的土体固有变异性;②设备、程序、操作员和随机测试影响引起的测量误差;③使用经验或其他相关模型将现场或实验室所得数据转化为所设计土壤性质时引起的转换不确定性。在岩土工程设计和计算研究领域,学者们也渐渐不再使用确定值来描述土体参数,而是采用随机分布的形式。Griffiths等[3]在进行随机有限元分析地基承载力时,采用对数正态分布来表征土体的强度指标c、φ值,取得了较好的计算效果。
现今国内外对于土体各种参数指标的统计分析研究,最基本方法是统计某一土体参数整体的均值、方差(或标准差)以及变异系数[4-5],也有按照数据来源将所研究参数进行分组,按照组别再统计均值与变异系数[1],这样能获得较多的均值与变异系数对应点;之后对于土体的概率分布统计特征研究,则通过常规的非参数或者参数方法。
非参数方法主要是频率分布直方图法,即采用柱状图表示频数和区间分布,如林鲁生等[6]使用频率分布直方图对某边坡抗剪强度参数进行了统计分析,Bilgin等[7]也用频率分布直方图统计了土样的CPT和SPT比值;而常用的参数方法则包括卡方检验法以及K-S检验方法,如渠时勤等[4]、唐芬等[5]分别对万州市区、重庆库区土体进行了卡方检验以研究其分布,陈立宏等[8]、张继周等[9]应用K-S法对土体参数的概率分布类型进行检验,而针对岩体参数的研究则有江权等[10]用K-S法检验了玄武岩对几种常见分布的符合情况。
但现今部分研究试验数据量有所欠缺,对于结果支持度不够;统计土体指标的方法仍然比较传统,非参数方法不能获取土体指标的概率密度函数,而参数方法如卡方检验、K-S检验效能不高,亟需提高参数方法应用的效能。
因此,本文以我国正在为伊朗建设的德伊高铁沿线所在地基土的大量实验室数据为依托,对沿线土体的物理力学参数进行统计分析,研究其变异性及利用概率密度估计方法分析其概率分布特征并进行随机分布检验。分析结果可以作为同种类土体随机有限元、可靠度分析参数选取依据,也可用作之后重塑土试验及其性质的对照。
1 土体参数变异性分析
德伊高铁项目起于伊朗首都德黑兰,经库姆,终于伊斯法罕,线路全长约410 km,其中德黑兰至库姆新建段约165 km、库姆至伊斯法罕整治段约245 km。本文分析所用数据来自德伊高铁沿线地基土的实验室测试结果,所有测试方法均按照美国材料实验协会(ASTM)标准进行;数据充分、样本量大,广度基本涵盖整条线路,对其进行分析可以得出较为可信的结果。
德伊高铁沿线土体以低塑性黏土(CL)、黏土质砂(SC)所占比例最大。CL土为不含有机质的淤泥或黏土,200号筛网(对应孔径0.075 mm)截留残余量在50%以下,塑性指数>7,在土壤塑性图中点落在“A线”之上,其中按照200号筛网截留残余量以及砂粒和砾粒含量的不同又可分为低塑性黏土、含砂低塑性黏土、含砾低塑性黏土、砂质低塑性黏土、含砾石砂质低塑性黏土、多砾石低塑性黏土、含砂多砾石低塑性黏土共7个更小的种类。SC土属于砂性土中的一类土,200号筛网截留残余量在50%以上,但其细颗粒含量超过12%,且细颗粒所处分类为CL或重黏土(CH),较为接近黏性土,其中SC土又可按照砾粒含量分为两个更小种类,砾粒含量小于15%为黏土质砂,砾粒含量大于或等于15%为含砾黏土质砂。通过筛分试验得到的现场CL、SC土样级配曲线见图1,包括94个CL土样本和39个SC土样本。按照各类颗粒含量划分的CL、SC类土的质地分级三角图见图2。

图1 现场CL、SC土样级配曲线

图2 CL、SC类土的质地分级三角图
本文主要针对这两种土体的物理力学参数进行统计分析,包括:天然密度、天然含水率、液塑限、塑性指数以及黏聚力、内摩擦角、压缩模量。
变异性的评价指标一般用变异系数来描述,即用数据的标准差与均值的比值表示为
(1)
式中:COV为变异系数;SD为样本标准差;Mean为样本均值,计算式为
(2)
(3)
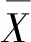
根据Phoon等[1]对土体变异性三大来源的阐述,本文分析的土体变异性将会包含土体固有变异性和测量误差,因此对上述参数变异性分析的结果将会比土体自身固有变异性偏大。
1.1 实验室基本物理参数指标变异性统计
本文所研究土体的实验室基本物理参数指标为天然密度、天然含水率、液塑限以及塑性指数。所有试验样本按照试验所在的里程进行分组,以每2 000 m作为每组数据的分界,即在同一2 000 m里程位置内进行的试验结果归为一组,以组为单位进行变异性统计。
本文对CL、SC土天然密度、天然含水率、液塑限试验结果和塑性指数进行了总结,试验数据样本数、组数和均值、变异系数范围,见表1、表2。
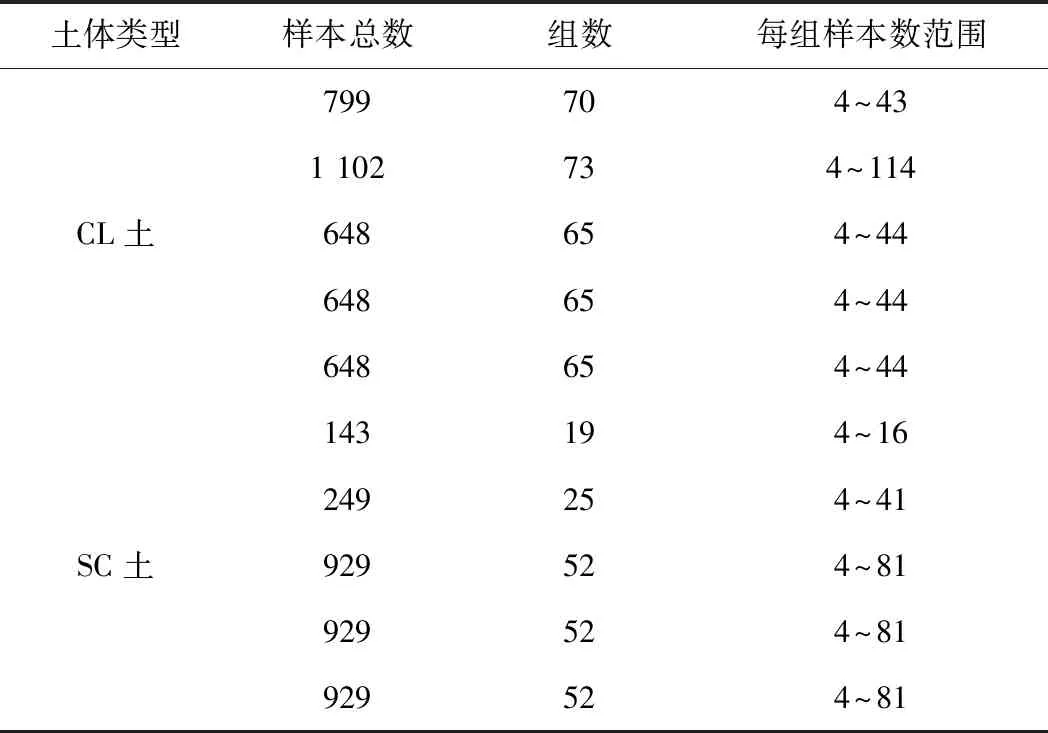
表1 CL、SC土实验室基本物理参数指标
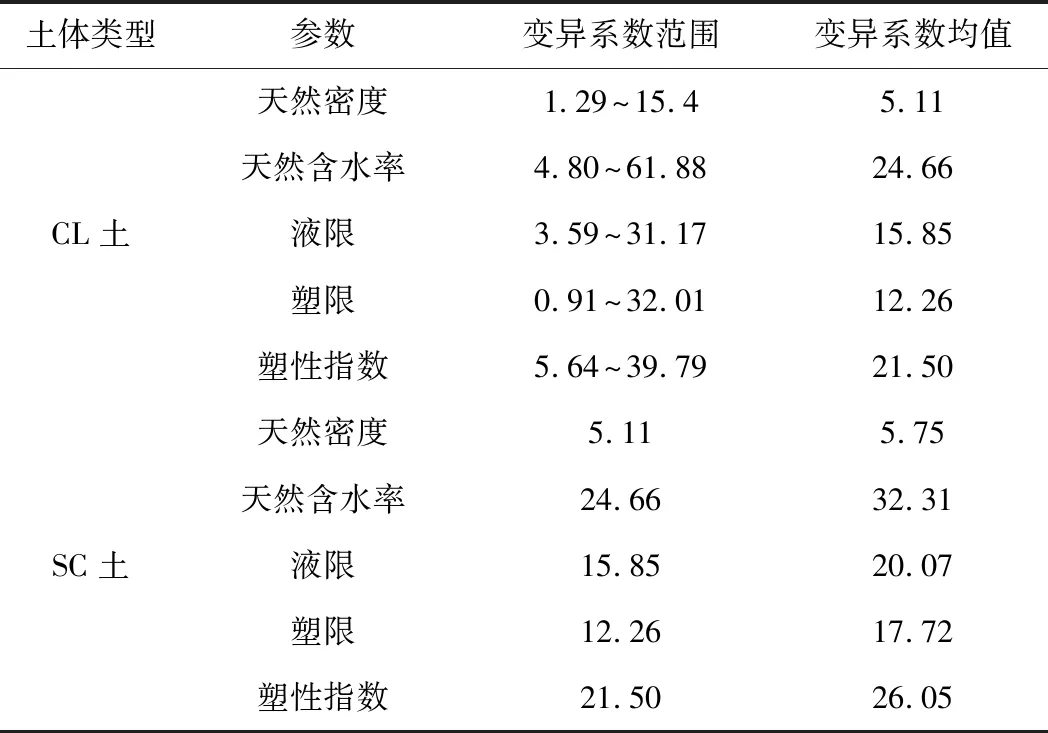
表2 CL、SC土实验室基本物理参数指标的变异性 %
CL、SC土的液限、塑限、天然密度、天然含水率和塑性指数的均值与变异系数关系见图3。
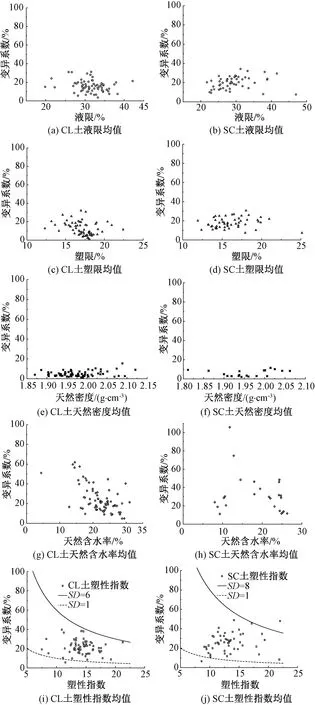
图3 土体实验室基本物理参数指标的均值与变异系数关系
由图3可知,无论何种土体,天然密度的变异性相较于其他参数,始终是最小的,变异系数不超过20%,且一般在10%以下。对于不同的土体样本,在众多参数中,密度的变化最小;甚至不同种类土体间,密度的变化也很小。原因为:根据统计的前期固结压力,整条线路相同土体所承受的前期应力历史大致相同,进而导致其密度的变异性较小。每种土体的液限和塑限分布图形比较相似,但液限均值分布范围比塑限更大,总体上两种土的液、塑限变异系数均不超过35%。两种土的塑性指数变异性都比液、塑限更大,但变异系数不超过50%,对CL土使用标准差为1、6的包络线以及对SC土使用标准差为1、8的包络线能将绝大多数点涵盖在内,因此这两种土的塑性指数在均值附近变化范围分别为±(1~6)和±(1~8)。天然含水率变异性在两种土的测试数据中都是最大的,且变异系数分布范围也很大,但是随着的天然含水率均值的增大,变异系数有减小的趋势。这种情况可能与伊朗所处半干旱地区有关:①一般地下土层含水率普遍不高,因此变异性容易受极端值控制而变大;②样本处于地下水丰富区域时,则含水率会显著增大,变异性不易受极干、极湿土样的影响,从而变异系数会变小。
1.2 实验室强度指标变异性统计
本文研究的土体实验室强度指标为:土体黏聚力、内摩擦角以及压缩模量,其中黏聚力和内摩擦角通过直剪试验中的快剪得到,压缩模量通过固结试验得到。
本文对CL土和SC土直剪黏聚力、内摩擦角以及垂直固结压缩模量试验结果进行了总结,试验数据样本数、组数和均值、变异系数范围见表3、表4。
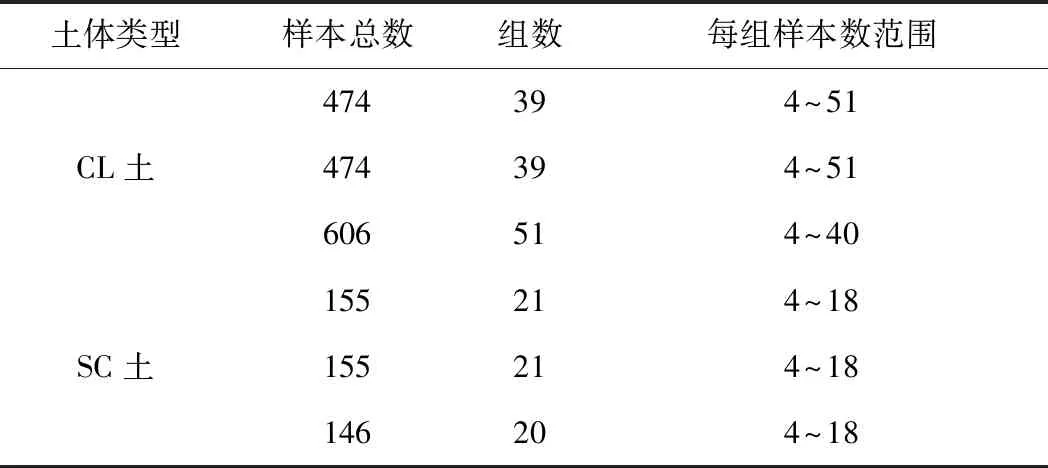
表3 CL、SC土实验室强度指标
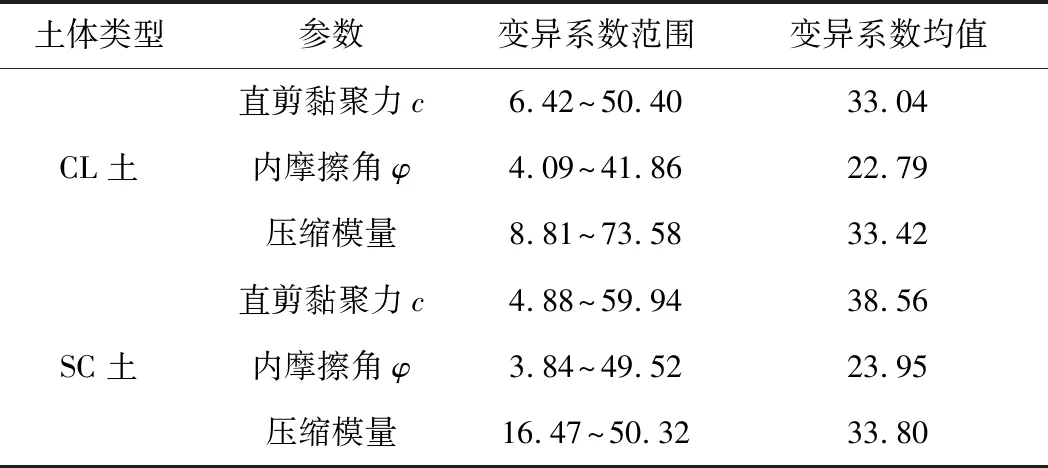
表4 CL、SC土实验室强度指标的变异性 %
CL、SC土的直剪黏聚力、内摩擦角和垂直固结压缩模量均值与变异系数关系见图4。由图4可知,CL土和SC土强度指标的变异性都比较大,均值和变异系数也在较大的范围内分布,且没有明显规律可循。两种土强度指标中,内摩擦角的变异性相对其他两个强度指标更小;除内摩擦角外,直剪黏聚力和压缩模量的变异系数均值比实验室基本物理参数指标变异系数均值都更大。
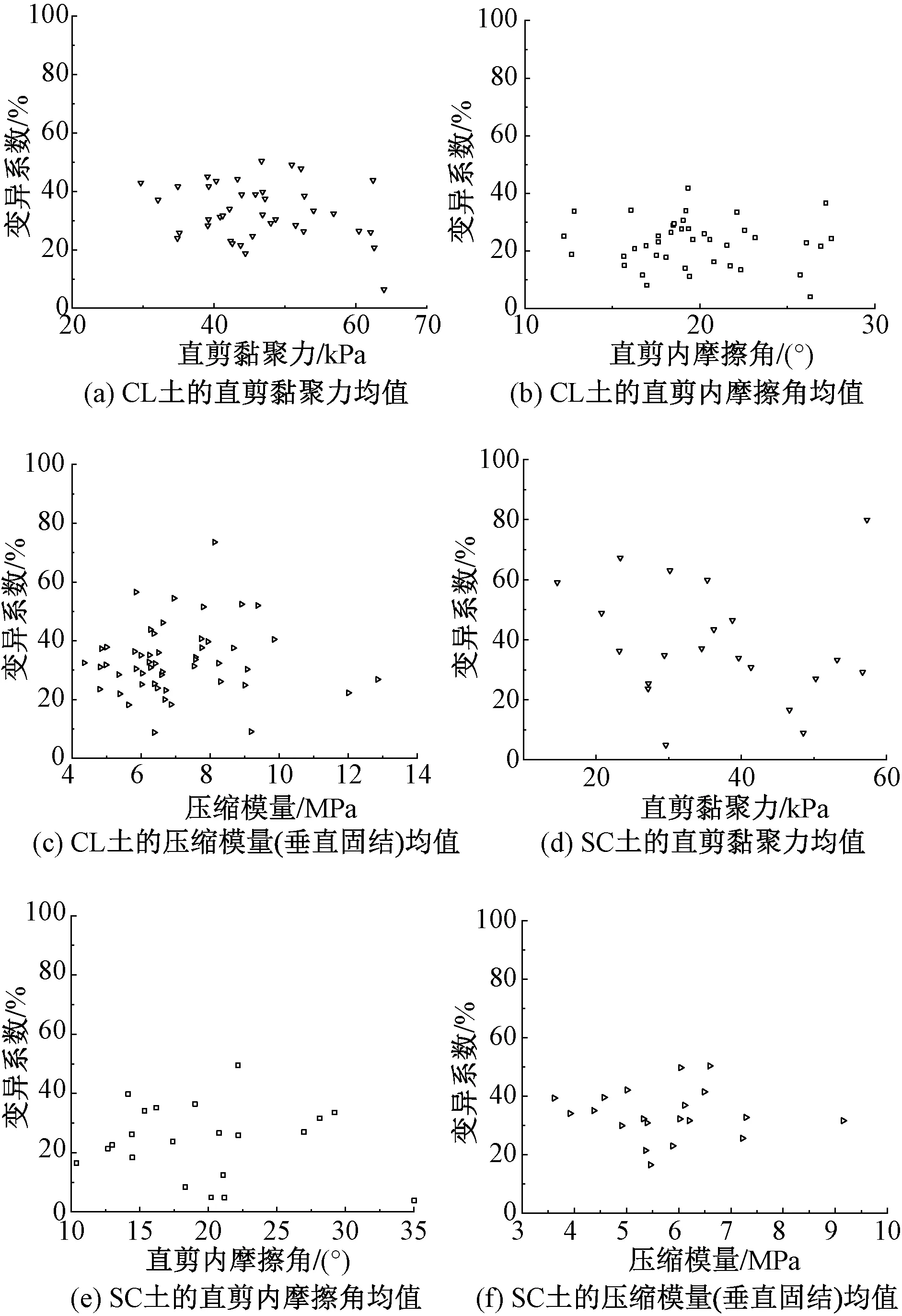
图4 土体实验室强度指标的均值与变异系数关系
试验所得强度指标部分数据结果的均值较为接近,但CL、SC土二者有显著差别,具体体现在以下两个方面:①液、塑限以及塑性指数。CL土的液限、塑限、塑性指数三个参数的平均值相比SC土都更大;②黏聚力。CL土黏聚力平均值显然比SC土大。上述指标越大则表示土体黏粒含量越多。但根据ASTM D2487-17规范[11]对CL与SC两种土体的定义,从粒径方面按照200号筛网截留残余量是否达到50%进行划分,残余量十分接近、粒径重合部分可能较多的情况不能忽视;且CL、SC两种土又可细分为许多种小的类别,涵盖的范围较广,存在交叉的部分。故二者有相似之处,所以导致其粘聚力、内摩擦角、压缩模量结果较为接近。
通过本文得出的基本物理参数指标和强度指标变异系数均值的综合比较,可以得出:德伊高铁沿线地基土中,CL土变异性比SC土更小。
2 土体参数概率密度及分布估计
通过一般的统计手段,已经初步获取了土体参数的均值和标准差,这是将土体参数应用在考虑了变异性的随机有限元以及可靠度分析的第一步。为了使随机有限元计算以及可靠度分析的结果更为准确,仅仅依靠均值和标准差是远远不够的,还需要明确土体参数每个值的分布区间,因此土体参数具体分布情况是不可或缺的。本文所用获取土体参数具体分布的方式有两种:①采用非参数方式估计土体指标的具体概率分布,直接用估计所得的概率分布函数表示土体指标的具体分布,而不借助其他随机分布表示;②假设土体指标服从某种随机分布形式,利用我们已经获得的数据对随机分布假设进行验证,验证结果满足分布,则得到土体指标服从这种随机分布的结论。
2.1 非参数方法——土体参数核密度估计
核密度估计法(Kernel Density Estimation)最早由Rosenblatt[12]和Parzen[13]提出,又称为Parzen窗法,由于此法不事先假定特定分布以及具体参数对数据进行分析,而直接根据所给数据样本估计指标的概率分布,因此属于非参数方法。相比利用参数方法假定数据参数模型进行评估,核密度估计法的结果更能符合研究对象的实际物理模型[14]。
核密度估计基本原理:
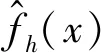
(4)
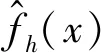
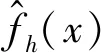
(5)
因此可将核函数选取为常用随机变量的概率密度函数,常用的核函数有高斯核函数(Gaussian kernel)、Uniform、Triangular、Biweight、Triweight、Epanechnikov等。本文所用核函数为高斯核函数,即正态分布的概率密度函数为
(6)
窗宽h的值对于最后的核密度估计结果也有很大影响,若窗宽h过大,则产生的概率密度估计曲线过分平滑,将忽略掉样本分布的重要特征;若窗宽h过小,则产生的概率密度估计曲线将会非常曲折陡峭;能将核密度估计函数与真实概率分布函数的误差降低到最小的窗宽称为最佳窗宽。Silverman[15]给出了求取高斯核函数最佳窗宽h(即使平均积分平方误差最小化窗宽)的经验法则,即
(7)
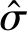
确定了核函数和窗宽之后便可以进行核密度估计,本文采用Python编程实现核密度估计。以CL土液限数据为例,样本数为799,标准差为0.128,由式(7)计算可得最佳窗宽为0.036。CL土和SC土各参数的最佳窗宽见表5。

表5 CL、SC土各参数的最佳窗宽
CL、SC土各项参数的核密度估计结果见图5。

图5 土体各项参数的核密度估计
由图5可知,各参数的概率密度分布函数相同点且形状基本表现为单峰,但是各参数彼此之间存在较大差异;同一种参数中,两种土的分布图形也有差异,但天然密度概率分布以及压缩模量概率分布比较类似。黏聚力、内摩擦角以及压缩模量呈现单峰以及正偏态分布形式,而在实际的随机有限元计算中也常将上述参数取为单峰、正偏态的对数正态分布形式,但若要明确上述参数是否符合某种分布,还需要进行分布估计检验。
2.2 土体参数分布估计的Anderson-Darling检验
Anderson-Darling检验由Anderson和Darling[16]提出,用于对样本分布假设进行拟合优度检验。Anderson-Darling检验相比传统检验方式如卡方检验χ2、KS(Kolmogrov-Smirnov)检验,检验效能更高[17],能够克服样本数量较少以及分布参数为未知等条件下传统检验方式不能检验的缺点。Anderson-Darling检验的基本原理为:通过比较样本的经验分布函数Fn(x)和所假设分布的分布函数F(x)之间的检验统计量与检验临界值的大小关系,在显著度水平α下,接受或者拒绝原假设H0,即判断样本是否满足特定分布。
Anderson-Darling检验统计量的具体计算步骤为
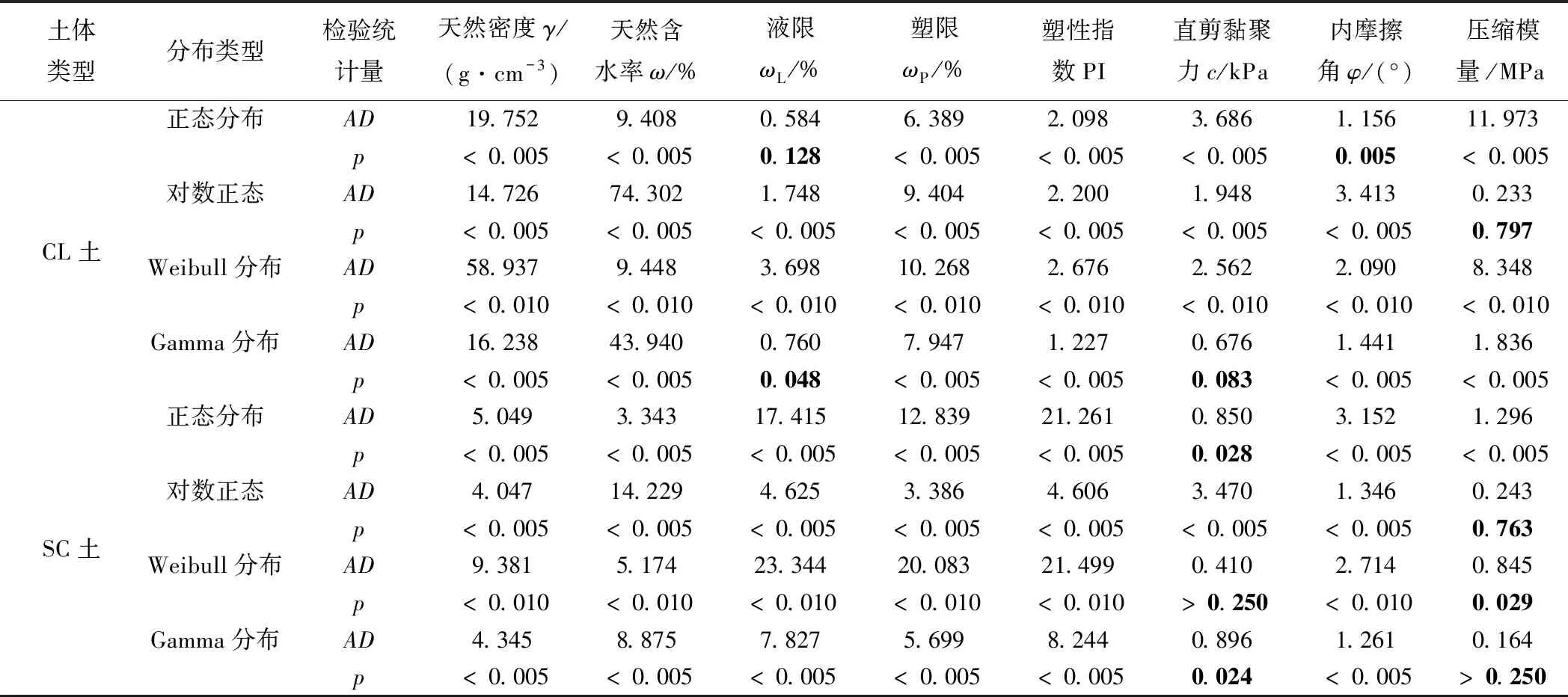
Step1已知n个样本数据在排序后x1 (8) Step2Fn(x)和F(x)之间的检验统计量AD为 (9) 实际应用中常使用离散形式计算检验统计量AD,即 (10) 经过证明,在原假设H0为真,假设分布函数F(x)为已知时,检验统计量AD与F(x)独立[18]。 2.1节的核密度估计得到了土体参数的概率密度分布函数,为了全面地分析确定本文所研究的两种土体各项参数的概率统计特征,采用Anderson-Darling方法,检验土体参数是否符合四种常见基本分布,即正态分布、对数正态分布、Gamma分布以及Weibull分布。 正态分布(也称为高斯分布)是最常见也是最多使用的统计分布。正态分布的概率密度函数为 (11) 如果ln(x-λ)具有正态分布,则变量x具有对数正态分布,其概率密度函数为 x>λσ>0 (12) Gamma分布通常用于模拟具有正向偏斜的数据的分布,其概率密度函数为 x>θa>0b>0 (13) Weibull分布的概率密度函数为 x≥λα>0β>0 (14) 式中:对于正态分布和对数正态分布概率密度函数,σ为标准差;μ为均值;λ为阈值参数。对于Gamma分布,a为形状参数,控制概率密度曲线形状,当a=1时与指数分布形状相同;b为尺度参数,可以缩小和放大坐标尺度;θ为阈值参数;Г为Gamma函数。对于Weibull分布,β为形状参数,当β=1时与指数分布形状相同;α为Weibull分布尺度参数。 CL、SC土各自8个参数对于上述4种基本分布:正态分布、对数正态分布、Gamma分布以及Weibull分布的Anderson-Darling检验结果分别见表6,进一步将检验统计量AD换算成p值,在显著度水平α=0.05条件下,若p<0.05,则拒绝所给分布假设,反之则认为参数符合给定分布。所有数据来源均为样本总体,样本总数见表1~表4。 表6 CL、SC土参数几种分布假设的Anderson-Darling检验 CL土的天然密度、天然含水率、塑限、塑性指数和直剪试验内摩擦角均不符合所给四种分布假设,而液限检验统计量AD=0.584,p>0.05,符合正态分布。同理,直剪黏聚力符合Gamma分布,压缩模量符合对数正态分布。而SC土的天然密度、天然含水率、液限、塑限、塑性指数和内摩擦角均不符合所给四种分布假设,而其直剪试验黏聚力符合Weibull分布。压缩模量既符合对数正态分布同时也符合Gamma分布。除黏聚力和压缩模量外,其余参数基本不能符合四种基本分布形式。出现这种结果可能的原因为:所有数据样本均没有考虑深度的影响,即样本来自所有深度,没有按照深度进行划分,而深度对于各项参数的影响是比较显著的;但通过固结试验获得的压缩模量对深度变化不敏感,所以比较能符合特定分布,如对数正态分布。 通过进一步研究可以发现,本文未使用的某些多参数分布假设对于所用样本的拟合优度可能更好,如三参数对数正态分布、三参数Weibull分布以及三参数Gamma分布,但是由于其复杂性,应用成本也较高。 (1)根据德伊高铁沿线所在地基土的实验室数据,统计了沿线两种主要CL、SC土的物理力学参数并分析其固有变异性:总体来看,实验室基本物理参数指标变异性相比除内摩擦角以外的强度指标变异性更小,其中天然密度变异性最小;若根据土的种类来分,则各项参数中CL土相比SC土的变异性都更小。 (2)利用核密度估计法对于所有样本对应的概率分布进行了估计,结果显示所有土体参数核密度统计情况基本符合单峰分布,但各项土体参数的核密度结果之间存在较大差异。本文还使用Anderson-Darling检验方法,对德伊高铁两种主要土体的各项参数是否符合特定分布进行了检验,发现大部分参数并不符合所给4种随机分布模型(正态、对数正态、Weibull、Gamma),其中实验室基本物理参数指标符合特定分布的最少,相反三个强度指标黏聚力、内摩擦角、压缩模量符合特定分布最多。利用核密度估计所得分布相比Anderson-Darling检验使用特定分布对样本进行拟合,更能符合实际情况,得到概率密度函数、体现具体分布的细节,使计算结果更准确,但是应用起来也稍为复杂。 土体变异性是其固有属性,且相比其他材料变异性更大,研究其变异性和分布形式是在岩土工程中开展随机有限元、可靠度分析的基础,本文分析结果可以作为德伊高铁项目中随机有限元、可靠度分析的土体参数选取依据,也可用作之后重塑土试验及其性质的对照。进一步的研究将需要来自更广泛地区以及数量更多的样本数据。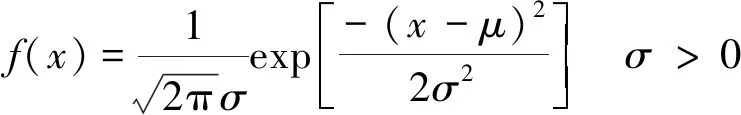
3 结论
