高速铁路定期票产品定价优化研究
2022-08-09苗蕾,王煜
苗 蕾,王 煜
(1.北京交通大学 交通运输学院,北京 100044;2.中国铁道科学研究院集团有限公司 电子计算技术研究所,北京 100081)
2020年起,铁路运输企业推出计次票、定期票等新产品,广受市场欢迎,尤其是定期票产品。定期票产品以“公交化、便利化出行”为设计理念,主要针对通勤旅客和部分商务旅客,通过“量多价惠”的原则吸引目标旅客,增加用户黏性,提高市场占有率。定期票持有者可在规定时间内乘坐规定次数,购买产品时指定发到站及席别的列车。旅客可按出行期限灵活选择产品,如5、10、30日定期票等。定期票产品推出时间较短,无直接“量化的定价理论”可供参考,价格制定还处在探索研究阶段,目前铁路定期票产品定价主要依靠各级价格管理人员的经验,缺乏量化的理论模型来确定定期票产品的合理价格,难以最大化铁路运输企业收益。
定期票在城市公共交通等领域已有应用,如公交、城市轨道交通等,多以周末票、7日票、月票等形式推出。但铁路定期票产品应用场景与上述公共交通票务产品区别很大,能够从中借鉴的极为有限,高速铁路(以下简称“高铁”)定期票产品定价是一项崭新的命题。另一方面,既有关于定期票产品定价理论研究较少,尤其是带有数据和模型支撑的量化理论研究几乎为空白,难以借鉴既有研究成果。
定期票定价属于铁路客运产品定价范畴,与铁路主流定价理论具有共通性。文献[1]研究交通运输产品即易逝品的定价问题。文献[2]研究不确定需求下单一产品定价模型。文献[3]构建基于多列车多停站的票额和票价综合优化模型,根据模型特点设计混合启发式算法,从而得到不同列车在不同区段的不同定价,解决差异化定价的问题。文献[4-5] 研究我国铁路实施客票折扣销售的可行性及相关折扣制定依据。文献[6]以时间敏感性、价格敏感性及出发时段偏好为基础,对旅客进行分类,再研究同一区段两列平行列车的动态定价问题。文献[7-8]首先模拟旅客需求函数,得到客运产品需求与票价的数学关系,再逐步构建高铁动态票价优化模型并求解。文献[9]以京沪高铁为例,考虑多种交通竞争方式,基于Logit模型构建票价与收入的关系范式,得到收益优化后的票价范围。文献[10]构建不同时刻、不同运输方式的旅客出行广义费用函数,建立双层规划模型,优化不同时段城际铁路票价。文献[11]依据最大凹向包络理论,建立基于乘客出行选择行为的动态定价策略模型。本文基于以上理论模型,研究单列车多停站定期票定价优化模型。
1 参数定义与假设
为研究定期票定价问题,对部分内容进行简化和假设:
①不考虑退票、改签对定价过程的影响。
②定期票定价基准对象是始发终到区间。
③每位旅客都是理性人,以自身利益最大化为出发点决策是否购买定期票,非始发终到旅客一般不会购买定期票,除非可以套利。购买定期票后旅客不会乘坐非始发终到的短区间。
④以二等座为研究对象。
主要变量及其含义见表1。

表1 主要变量及定义
2 模型构建
2.1 旅客需求分析
旅客根据其乘车历史判断是否购买定期票,对于某列车始发终到区间来说,旅客决定购买定期票的原因:①自身历史参考期(某个时间段)内实际乘车花费高于定期票价格,购买定期票产品划算;②更加便捷(随时预约席位,预约最多10个席位,不用每次提前购票,提高乘车效率),部分旅客考虑定期票出行的便捷性,同时考虑到自身在历史参考期的花费仅略低于定期票价格,决定以提高少量花费换取乘车便捷性从而购买定期票产品;③部分旅客虽然在历史参考期实际花费低于定期票价格,但定期票单次乘车价格下降会使这部分旅客预期增加乘车次数,从而购买定期票。对于情况②和③,旅客在历史参考期的实际花费比较接近定期票产品价格才有可能最终选择购买定期票产品。本文引入预期系数概念β对情况②和③的旅客在历史参考期的实际花费接近定期票产品价格的程度进行度量,再结合情况①得到定期票旅客判别条件Φ为
(1)
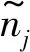
(2)
(3)
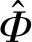
(4)
(5)

(6)
(7)
(8)
式中:μ1、σ1分别为该正态分布的均值、标准差。
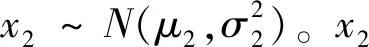
(9)
(10)
(11)
式中:μ2、σ2分别为该正态分布的均值、标准值。
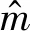

(12)
式(12)表示定期票旅客在购买定期票后相对于历史参考期乘车次数会调高自己在时间段t内的实际乘车次数。时间段t内,如果(r,s)为非始发终到区间,则(r,s)只有非定期票旅客乘车需求,其客流需求假设服从独立的正态分布,则其客流需求概率密度函数为
(13)
式中:μrs、σrs分别为该正态分布的期望和标准差。
区间(r,s)期望售出数量Qrs为

(14)
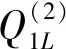
(15)
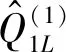
(16)
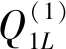
(17)
时间段t内总定员Ct为
Ct=t·C
(18)
式中:C为列车定员。
同时以上分析需要满足约束
(19)
(20)
(21)
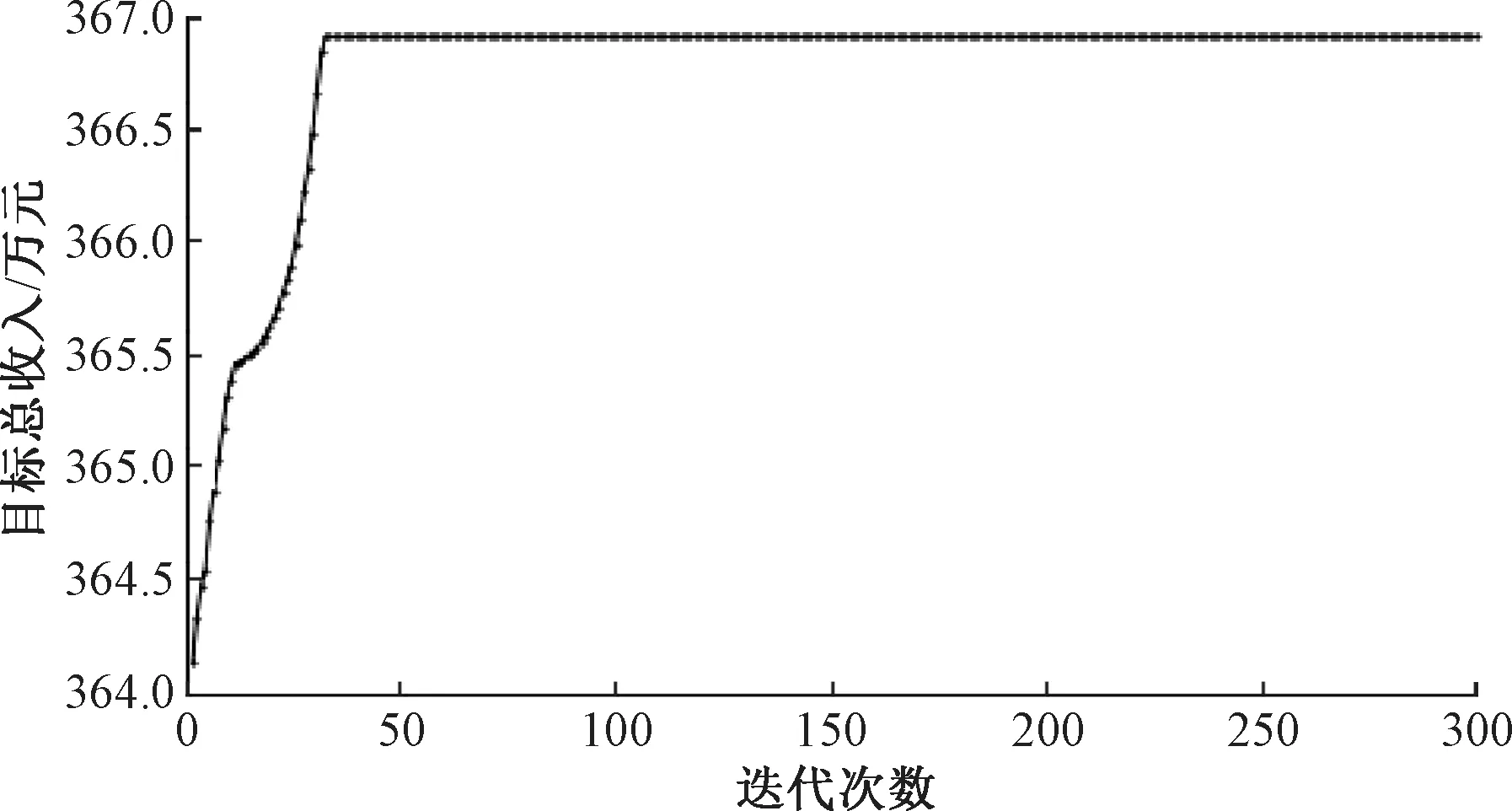
qrs∈N 1≤r (22) 式(18)~式(20)为列车能力约束,式(21)为定价约束,式(22)为整数约束。 对于铁路运输企业,在时间段t,始发终到区间定期票产品提供的收益R1为 (23) (24) 非始发终到区间收益R2为 (25) 最终单列车多停站下的定期票定价优化模型为 (26) s.t. 式(18)~式(22) 模型是带约束条件的随机非线性规划模型,需要选择启发式算法求解。粒子群算法具有迭代过程简单、易于理解、依赖参数少等优势,可兼顾求解复杂度和效率,采用粒子群算法对模型求解。 式(26)需要同时优化定期票票价和票额两个变量,为简化后续求解,降低解向量的维度,先将所有非定期票旅客的收益计算公式合理转化为等效模型[13]为 (27) s.t. 式(20)、式(22) q1L≥μ2 (28) (28) 式中:gh为与A维度相同的向量,各分量服从(-d,d)上的均匀分布,d为整数。 (29) (30) (31) (32) h=1,2,…,Psize (33) 图1 求解过程 由于目前定期票推出的时间还太短,还多旅客还不了解定期票产品,真实销售数据还不能反映真实的需求;同时为简化问题复杂度,提高模型迭代效率,基于本文假设的统计学分布生成模拟数据对单列车多停站下的定期票定价优化模型进行算例分析。假设定期票设定乘车有效期为10 d,t=10。允许最大乘车次数为10次,m=10。定期票乘车区间为北京南至上海虹桥,涉及唯一列车为G22。G22定员1 103,C=1 103。经停南京南站,共涉及3个区间:北京南至上海虹桥,北京南至南京南,南京南至上海虹桥。取J=2,北京南至上海虹桥区间旅客乘车次数分布见表2、表3。 表2 第1个标本时间段旅客乘车次数分布 表3 第2个样本时间段旅客乘车次数分布 北京南至南京南、南京南至上海虹桥发送量均值和标准差数据见表4。 表4 非始发终到区间客流量 人次 各区间票价见表5。 表5 各区间票价 根据铁路客运一线价格管理人员的专家经验估算预期系数β=1.5,激励系数α=1.2。定期票价格上限为正常乘车总价格即6 310元,为了防止非始发终到区间旅客通过购买始发终到区间定期票套利,也为了打消购买定期票旅客乘坐非始发终到短区间的可能性,需要分析定期票最低限价,非始发终到区间中最高票价区间为北京南至上海虹桥,票价为504元,因而定期票下限(乘坐10次)为5 040元。 利用Python实现求解过程,设定粒子规模Psize=20,最大迭代次数为300次,收敛控制系数δ=1,φ1=0.5,φ2=0.5。以正常乘坐9次价格5 679元和定期票潜在旅客数量样本均值82作为初始解输入模型求解。迭代过程见图2,可知在迭代到40次左右时达到收敛,最终定期票价格5 678元,取得总收入366.8万元。各区间票额分配结果见表6。 图2 算法迭代过程 表6 各区间票额分配结果 从表6可知,以10 d为定期票使用期限,需单日分配给北京南—上海虹桥定期票旅客席位126个。对于非定期票旅客,北京南—上海虹桥分配票额3 917张,北京南—南京南分配票额6 445张,南京南—上海虹桥分配票额6 445张。最终。以不推出定期票所有区间票额正常售出为对比方案,在t1和t2两个样本期平均收入为360万元,可知本文推出的定期票产品5 678(10,10)可以帮助铁路运输企业提高收入1.9%。 本文以解决客运价格管理实践中的实际问题入手,提出一种针对定期票产品定价的优化模型。首先假设旅客需求呈现正态分布,其次引入预期系数与激励系数模拟旅客决策行为从而得到定期产品的潜在旅客需求函数,最后以收益最大化为目标构建基于单列车多停站的定期票定价优化模型并求解。该模型将现有铁路定价理论与实际应用场景相结合,保证一定程度的落地应用,为各级价格管理人员提供了一种定期票定价决策方法,弥补了目前定期票产品定价过程中过于依靠人工经验的瑕疵。算例模拟结果表明通过本文提出的定期票定价模型能够提高总体收益1.9%,保证铁路运输企业继续扩大推广定期票产品的积极性,同时也为通勤旅客带来更适合的运输产品,增强铁路市场竞争力,实现铁路运输企业与旅客的双赢。 但是,本文是以单列车多停站下的应用场景,与多列车多停站的实际应用场景还有差距。同时,本文的假设也与实际条件有一定差距,尤其是旅客会在购买定期票后在短区间乘车这一现象会使得本文研究问题更加复杂,这些都是下一步需要深化研究的。2.2 定期票定价优化模型
3 模型求解


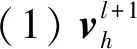
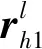

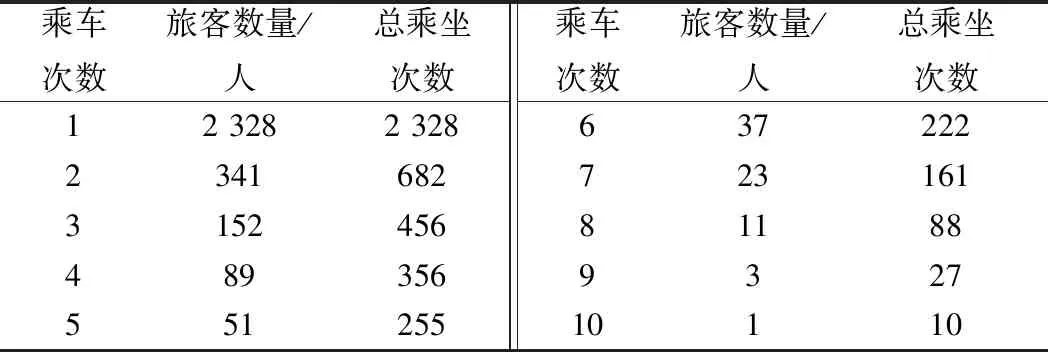
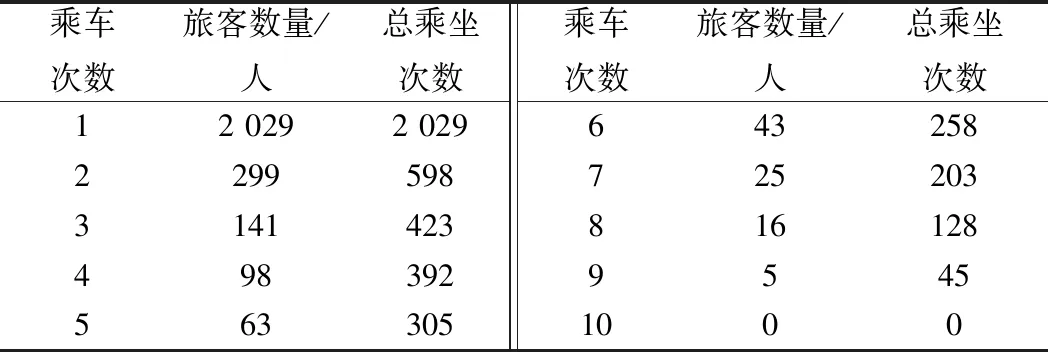
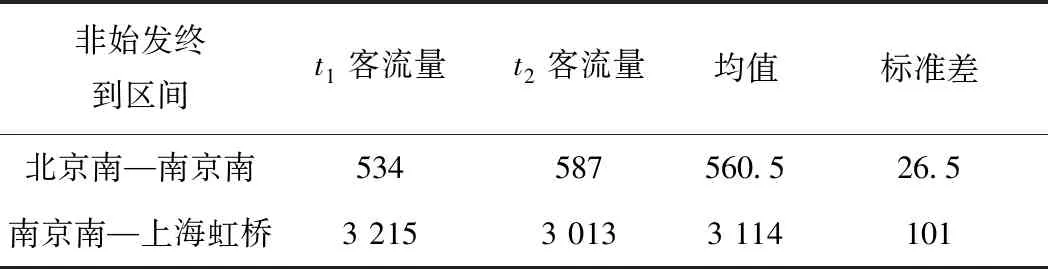
4 算例模拟


5 结论
