基于价格-时空网络的高速铁路票价优化研究
2022-08-09王怀相安仲文魏玉光
夏 阳,王怀相,周 茵,安仲文,魏玉光
(1.中国铁道科学研究院集团有限公司 运输及经济研究所,北京 100081;2.中国国家铁路集团有限公司 客运部,北京 100844;3.北京交通大学 交通运输学院,北京 100044)
我国2016年起明确放开高速铁路(以下简称“高铁”)动车组的票价管理权限,实行由铁路运输企业依法自主制定的政策。价格政策的放开,为高铁票价市场化改革提供了法律依据和政策支持,推动了铁路企业打破票价形式单一的限制,铁路企业开始积极尝试以市场为导向的票价机制改革实践,例如在高铁动卧产品及部分高铁线路上采取差异化票价策略。然而,我国高铁票价市场化改革还处于起步探索阶段,尚未形成完善、成熟的票价优化理论与技术体系。因此,健全高铁票价体系、合理确定票价水平、充分发挥企业市场主体地位,已成为我国高铁亟待解决的关键问题。
高铁票价优化属于收益管理范畴。收益管理最初应用于航空领域,发展至今已较为成熟。然而与航空运输相比,铁路运输服务网络及资源与产品映射关系更复杂,实施收益管理难度更大,导致铁路收益管理发展较为缓慢。尽管目前已有部分学者针对高铁票价进行了优化研究,但总体上仍处于研究初期阶段。考虑到旅客异质性,文献[1]研究旅客出行选择行为机理,分析票价变化如何影响旅客选择行为。文献[2-3]利用Logit模型研究竞争环境下铁路票价对客流分担率的影响。文献[4]根据平均列车上座率划分客流时段,构建城际铁路分时定价优化模型,并设计混合启发式算法进行求解,但未能综合考虑每列车的服务属性。文献[5]研究高铁差异化定价,构建双层规划模型,并利用启发式算法求解,但仅优化某一具体的始发-终到站(OD)。文献[6-7]分别对荷兰和中国铁路的高峰、低谷时段差异化定价问题进行优化研究,结果表明低谷时段的降价策略更利于提升经济效益。文献[8]在旅客分类的基础上,研究高铁动态定价问题。文献[9]运用前景理论,针对不同类型列车的差异性,构建高铁动态定价随机规划模型。文献[10-13]对高铁动态定价与票额分配进行协同优化研究。文献[14]对高铁票价和时刻表进行协同优化研究。文献[15]在文献[14]的基础上考虑票价对公平性的影响。
既有研究中仅少数学者研究高铁系统的公布票价[2-3],未考虑不同列车间的差异化定价。随着高铁建设和运营管理的不断发展,越来越多的学者开始研究高铁差异化票价,以期利用票价调控客流,提高经济效益,从而提升高铁的市场竞争力。根据是否考虑票价在售票期内的动态变化,可将既有研究分为两大类:①静态差异化定价方面,部分是以某一个OD为对象,来制定某一时段或不同列车的票价[4-5],虽优化了每列车在各服务OD间的票价,但构建的模型为非线性化模型,往往需要通过启发式算法求解,无法保证解的质量[6-7];②动态定价方面,依然存在模型非线性化导致需使用启发式算法求解的问题[8-13]。
高铁的静态差异化定价问题实质上是高铁列车服务网络上的配流问题,由于价格的浮动性质,其服务网络应拓展为能体现不同价格等级特点的多维时空网络。在此理论基础上,针对既有研究的不足,本文①通过设置离散价格策略,在列车服务网络基础上引入价格维度,构建了价格-时空三维网络;②将高铁静态差异化定价问题转化为考虑时空资源限制的多商品流问题,同时考虑客流守恒、列车能力、旅客有限理性选择等约束,建立高铁票价0-1整数线性规划模型;③为突破大规模网络问题受限于求解器计算能力的瓶颈,提出基于拉格朗日松弛的求解算法,通过将原始问题分解为相互独立的子问题,并设计相应的上界启发式算法,能够获得可行解与上界解之间的误差率,以评估求解质量。
1 问题描述
1.1 旅客分组
旅客在出行时,会综合考虑旅行时间、票价、出发时刻等因素,选择出行成本最小的方案。在扁平化票价策略下,影响旅客选择的主要因素是时间(旅行时间、出发时刻等)。采用差异化票价策略后,列车在同一OD间的票价不同,从而对旅客出行选择行为产生较大影响。在研究过程中,若对每个旅客单体分别建模,会导致模型规模过大,难以求解。因此采用旅客分组技术。
旅客对价格的敏感程度具有差异,收入是影响这一程度的关键因素之一。根据收入水平将旅客分为高收入、中收入、低收入3个等级,不同等级旅客具有不同的价格敏感度。显然,低收入旅客对票价的敏感性要高于高收入旅客。在此基础上,考虑旅客出行OD和期望出发时间:g为旅客组,g=(o,d,m,π);o为旅客始发车站;d为旅客终到车站;m为收入层级,m∈{1,2,3},1、2、3分别为高、中、低收入层级;π为期望出发时刻;G为旅客组集合,g∈G。
每个旅客组中的旅客具有相同的期望出发时刻和收入水平,因此其感知出行效用的能力相同,即乘坐同一列车出行成本相等。当面对多个可乘坐列车时,同一组内旅客倾向于选择同一列车(对其而言出行费用最小的列车)。因此,本文假设每个旅客组不可分割,在建模过程中仅需考虑各个旅客组,从而降低问题规模。
1.2 价格-时空网络构建

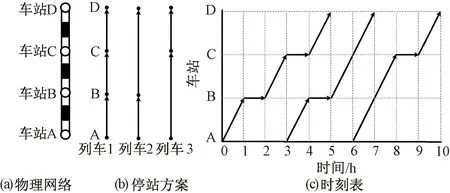
图1 简单高铁物理网络及其列车运行计划
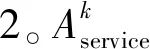
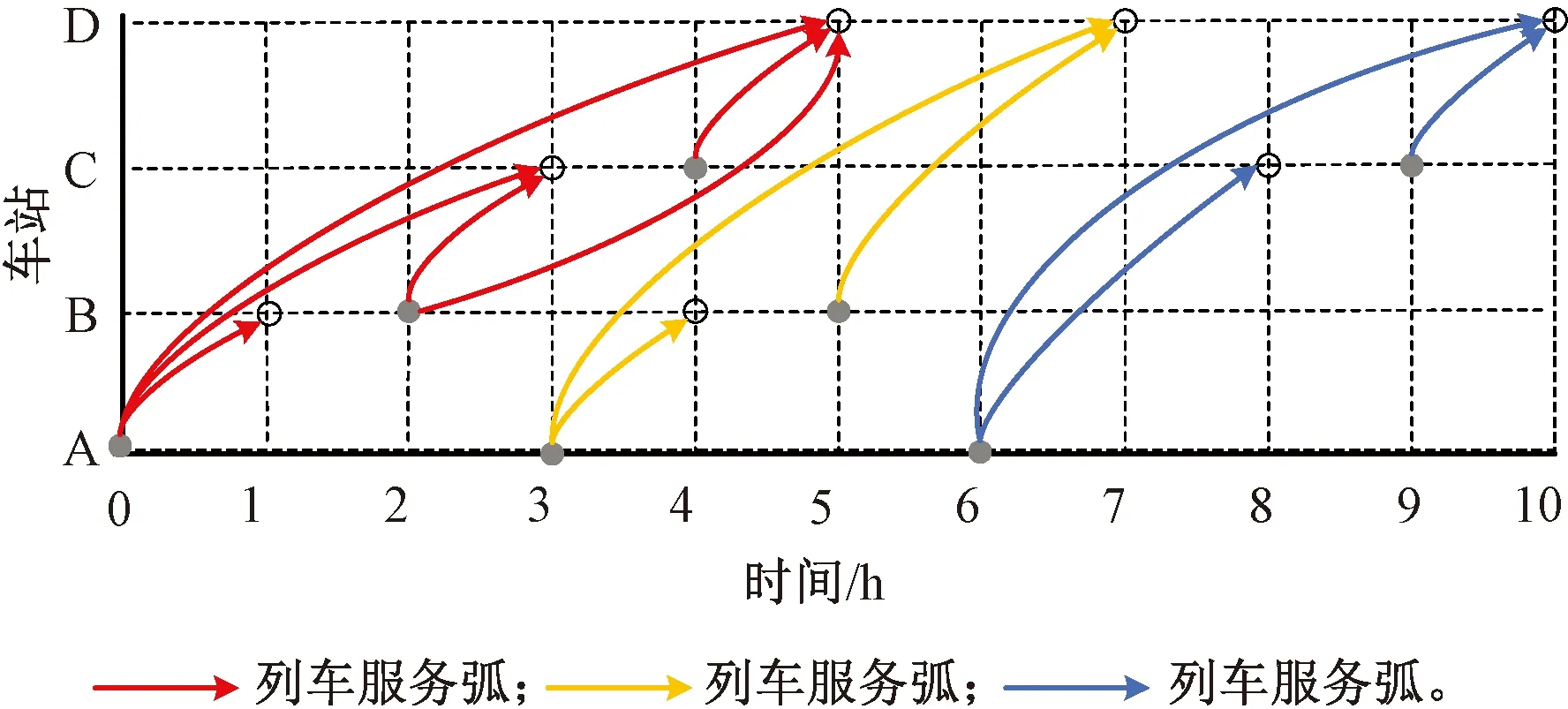
图2 列车服务时空网络
为提升高铁经济效益,采用差异化票价策略,即对于同一OD,不同列车上的票价并不相同,具体方法是设置不同的离散价格等级。N为价格等级集合,N={1,2,…,n,…,|N|};wn为价格等级n∈N所代表的具体价格策略,如增加10%、维持原价和降低10%等。价格等级集合N决定了票价的变动界限和取值范围,应在综合考虑政策文件、铁路公司要求和市场需求的基础上确定。基于列车服务时空网络,通过引入价格等级维度,可构建与图1相对应的三维价格-时空网络(V,A),见图3[17]。图3中,V为时空网络中的点集合;A为弧集合,图中为了统一标识服务弧,未区分不同列车的物理服务弧段颜色。
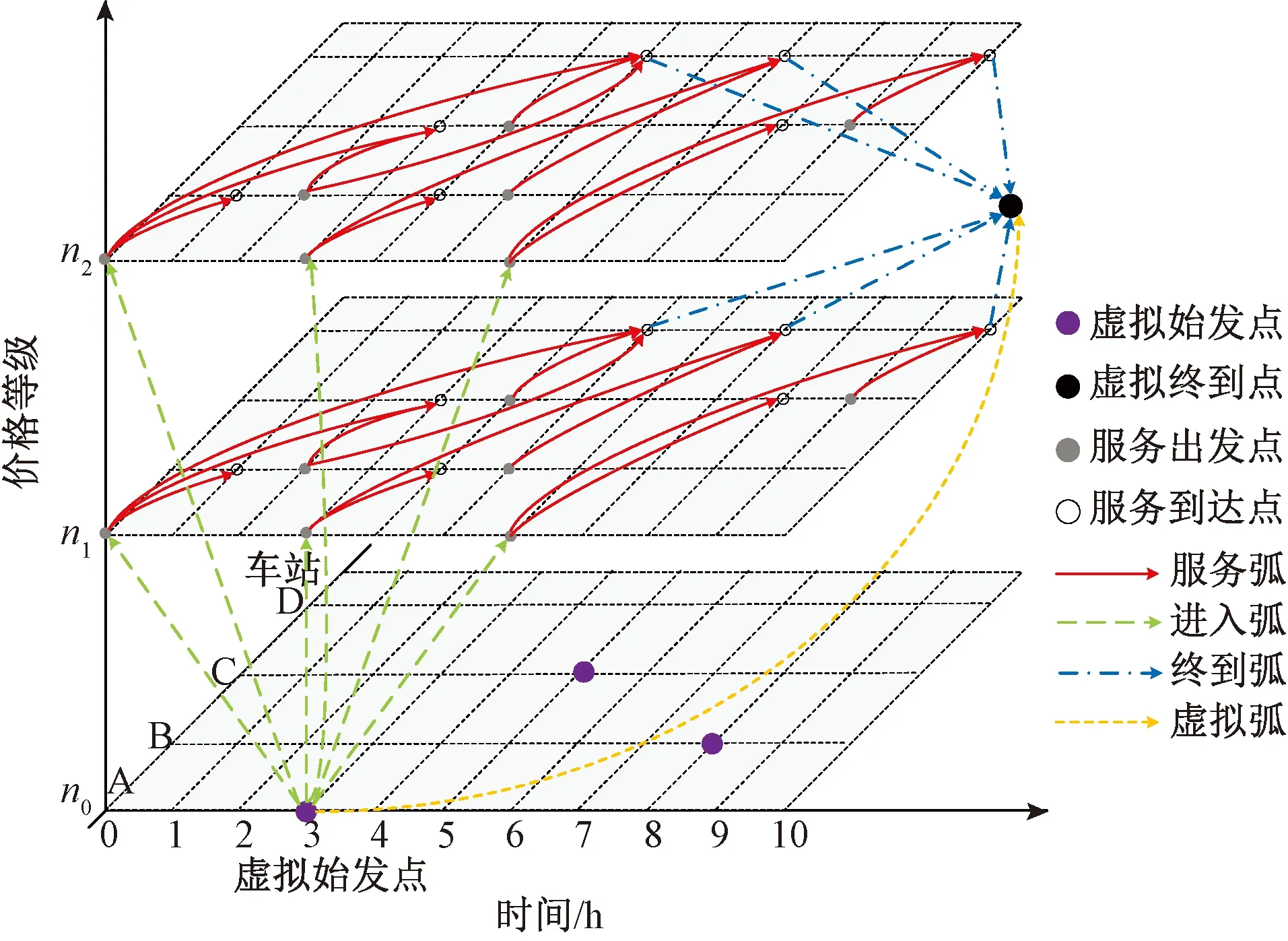
图3 价格-时空网络
图3包含了2个价格等级层n1、n2和一个虚拟始发层n0,各价格等级层具有相同的列车服务时空网络。价格-时空网络中节点集合V由4个子集合组成,分别为:
(1)虚拟始发点集合Vsource={(i,t,n0)|i=o(g),t=π(g),g∈G},式中:o(g)为旅客组g的始发站点;π(g)为旅客组g的期望出发时刻。所有旅客的虚拟始发点都落在虚拟始发层n0。
因此,V=Vsource∪Vsink∪Vde∪Var。可以看出,每个旅客组在价格-时空网络中均有相对应的虚拟始发点和终到点,并且与其自身属性(始发站、终到站、期望出发时刻)相一致,从而能够便于完整准确地刻画每个旅客组的出行路径。
价格-时空网络中弧段集合A主要包含进入弧、服务弧、终到弧以及虚拟弧,具体如下:
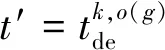
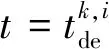
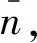
为了有效计算旅客出行路径的效用(成本),对价格-时空网络中各弧段的费用进行如下设定:进入弧的费用由两部分组成:①实际出发时间与期望出发时间之间的偏差;②列车旅行时间(每条服务弧与具体一列列车对应);列车服务弧的费用是票价;终到弧的费用为0;虚拟弧的费用为旅客可承受的出行成本上限。综上,价格-时空网络中各弧段的费用为
(1)

f(i,j,t,t′,n,n′)单独表示旅客使用各弧段(i,j,t,t′,n,n′)所带来的收益,即
f(i,j,t,t′,n,n′)=
(2)
1.3 研究问题
一般情况下,客流时空分布并不均衡。具体地,在一天的各个时间段内,客流量往往存在较大差异,从而产生了客流高峰期和低谷期。在客流低谷期内,列车上座率可能较低,既影响资源利用效率,又不利于提升经济效益;而在客流高峰期,由于列车能力限制,可能导致部分高铁客流流失。此外,旅客出行时,并非仅考虑具有最小成本的交通方案,而是会在自身可承受的出行成本范围内进行合理选择。因此,本文的目标是通过合理制定各列车的票价,来控制不同旅客的出行成本,实现“削峰填谷”,一方面最大化客票收入,另一方面减少旅客流失,提升列车能力利用效率。
在构建价格-时空网络后,旅客出行选择可视为在网络中选择一条合理的出行径路。由于对网络中各弧段设置了相应的成本和收益,因此每一条出行径路的成本和产生的客票收入均可计算。同时,旅客在选择出行径路时会受到列车能力、出行总成本等因素的限制。当出行成本高于其可承受的最高值或列车能力不足时,部分旅客将流失,即选择其他交通方式出行。因此,基于价格-时空网络,高铁的静态差异化定价问题转化为考虑时空资源限制的多商品流问题。
2 高铁差异化票价优化模型
2.1 模型假设
①各OD间期望乘坐高铁的客流已知,即潜在的客流需求给定。
②通过问卷调查等方法可以获得旅客的收入水平和期望出发时刻信息。
③仅考虑线路的一个列车运行方向,相反方向可采用同样方法处理。
④每个旅客组不可分割,即选择相同径路出行。
⑤各OD间旅客均匀到达。
2.2 符号、参数和变量说明
符号、参数和变量及含义见表1。决策变量及含义见表2。

表1 符号、参数说明

表2 变量说明
2.3 模型构建
目标函数为
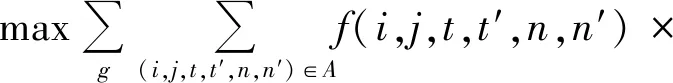
xg(i,j,t,t′,n,n′)×rg
(3)
式(3)表示总客票收入最大。
约束条件如下。
(1)流平衡约束
(4)
式中:(i=o(g),t=π(g),n=n0)、(i=d(g),t=T2,n=n)为旅客组g的虚拟起始点和终到点。
该约束规定了旅客组出行路径的完整性,且每组旅客只能选择一条出行路径。
(2)列车能力约束
rg≤cap(k) ∀k∈K∀(i′,j′)∈E
(5)
该约束规定了所有列车在各区段运输的旅客总量不得超过其最大运载能力。
(3)旅客有限理性约束
旅客有限理性约束在文献[16]中提出。本文在参考该文献的基础上构建为
xg(i,j,t,t′,n,n′)+βg×
(6)

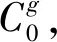
(4)变量关联约束
∀(i,j,t,t′,n,n)∈Atr
(7)
式中:M为一个极大常数。
该约束表示只有当服务弧(i,j,t,t′,n,n′)开放时(对应列车在该OD使用价格策略n),旅客组g才能选择该弧段,即出行路径中可包含该弧段;否则,旅客组将选择其他路径出行。该约束仅仅作用于服务弧,其他弧段不受约束,原因在于决策变量y(i,j,t,t′,n,n′)仅对应每个服务弧段。
(5)价格策略约束
(8)
该约束规定了不同价格等级层上的同一列车服务弧段,只能选择开放一个,即列车k在OD对(i,j)上只能采用一种价格策略,从而保证所有旅客均以相同价格购买该车票。
(6)价格逻辑约束
(9)
该约束规定里程长的OD票价要高于里程短的OD票价,避免旅客套利行为。
3 拉格朗日松弛求解方法
在二维时空网络中,本文采用物理服务网络,各列车的服务弧确定,且数量有限。与传统时空网络相比,也无需考虑列车径路的优化(仅优化旅客路径),也就无需建立数量庞大的列车停站、等待、运行弧等。此外,本文通过采用旅客组技术,进一步降低问题规模。综上,本文建立的价格-时空网络所含弧的数量较少,问题复杂度也较低。
拉格朗日松弛算法将原问题中的困难约束,通过设置拉格朗日乘子松弛至目标函数中,从而将原问题分解为多个易于求解的子问题。通过求解拉格朗日松弛问题,可以获得原问题的最优边界,并且经过乘子的不断迭代更新,松弛解将逐步逼近原问题的最优解。综上,考虑到模型的结构特征、变量类型以及约束形式,本文采用拉格朗日松弛算法求解模型。
3.1 模型分解
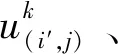
(10)
基于决策变量,松弛后的问题可分解为两个子问题Fx和Fy。
子问题Fx为
(11)
约束为式(4)。
由于只有服务弧的收益大于0,因此在式(11)中未考虑其他弧所带来的收益。
子问题Fy为
(12)
约束为式(8)、式(9)。
子问题Fx为|G|个相互独立的最短路径问题,可利用标号设定法求解;子问题Fy可用求解软件(如Cplex)求解。
3.2 上界启发式算法
通过求解两个子问题可获得下界解,但该解可能由于违反约束条件规则是非可行解。因此,本节设计启发式算法得到上界可行解。该算法根据获得的上界解中的旅客路径信息,初始化票价策略,并寻找出不满足列车能力约束和有限理性约束的旅客,将其分配至出行成本最小的可行路径中,最后寻找各列车可以采用的最优价格策略。算法步骤如下:
Step1价格策略初始化。基于求解子问题Fx获得的各OD间旅客组的出行径路,将路径中的价格等级层均调整为1(采用最低折扣的优惠),从而保证价格策略的唯一性。
Step2检索出行成本过高的旅客组。基于调整后的旅客组路径信息,计算每个旅客组的出行成本,若某旅客组出行成本大于其最高可承受值,则将该旅客组加入待分配集合中,并更新服务弧流量。
Step3检索使列车能力过载的旅客组。依次检测每列车每个区段,当某区段能力过载时,按组人数降序将相应旅客组加入待分配集合,直至符合能力约束。

Step5确定价格策略。基于客流分配结果,对每列车每个服务OD间的价格进行策略提升检测,即逐步提升价格策略等级,并测算是否旅客组的新出行成本均小于最大承受值,若满足,则继续提升策略等级;否则确定该列车该OD间的价格策略。
Step6计算上界,并更新上界可行解。
3.3 算法框架
算法整体步骤为
Step1初始化。令迭代次数z=0;拉格朗日乘子为0;初始化下界LB*=-∞;初始化上界UB*=+∞。
Step2求解下界解。
Step2.1利用标号设定法求解子问题Fx。
Step2.1利用CPLEX求解子问题Fy。
Step3求解上界可行解。利用3.2小节提出的启发式算法求解上界可行解。
Step4更新上、下界解。更新下界LB*=max{LB*,LBz},更新上界UB*=min{UB*,UBz}。
Step5更新拉格朗日乘子。
Step5.1
其中,θz为第z次迭代时的步长,θz=1/(z+1)。
Step5.2
c(i,j,t,t′,n,n′)×xg(i,j,t,t′,n,n′)+βg×
Step5.3
Step6终止条件判定。若迭代次数达到上限H,则终止算法;否则z=z+1,返回Step2。算法在迭代次数达到设置上限H时终止。
4 案例分析
本文使用Python编程语言实现提出算法,所有实验均在一台Intel Core i5-8265U CPU @1.60 GHz,8 GB RAM的计算机上进行。
4.1 输入数据
(1)列车运行数据
以京沪高铁2021年10月25日6:00—12:00运行的18列车为对象进行案例分析(仅考虑本线北京南—上海虹桥区间的列车)。考虑到列车在廊坊站、泰安站、滕州站、蚌埠南站、滁州站、定远站及丹阳站的总停靠次数均小于3次,这些站点产生客流量较小,故在案例分析过程中将不考虑这些车站。所有列车的停站方案以及在各站点的到达和出发时刻见图4,图4中车站名称后的数字为车站编号。

图4 案例列车的停站方案及在各站的到达和出发时刻
(2)客流数据
由于篇幅限制,无法列出所有旅客组的信息,在此重点介绍旅客组的生成过程:
①6:00—6:59和11:00—11:59为客流低谷期,7:00—10:59为客流高峰期。
②根据停站方案和时刻表依次为每一列车生成其服务OD间的客流。
③规定各OD旅客期望出发时间为列车在其出发站点的发车时刻。
④将各OD间的旅客平均划分为3个旅客组,分别表示高、中、低收入旅客。
需要说明的是,在第二步生成各OD间客流时,本文控制低谷期客流量小于列车能力,而令高峰期客流数量接近或超过列车能力。
此外,扁平化票价策略下的旅客组的最短路成本可通过标号设定法获得,在此不详细列出。
(3)票价数据
各OD间的原始票价来自12306官方售票网站。2019 年12月开始,我国对高铁线路执行票价进行优化调整,将执行票价设置为5~7 档的浮动体系,最大浮动范围是最低档为最高档的5.5 折,浮动范围大约在40%左右。同时,考虑到价格等级若设置过细过多,会导致问题复杂度急剧增加。综上,本文考虑票价等级N={1,2,3,4,5},即设定降低20%、10%、维持原价、增长10%、20%共5种票价策略。
(4)其他数据
实施案例所需的其他参数设定情况见表3。具体地,由于旅客出行目的和自身习惯属于较为隐私的信息且难以获取,本文参考文献[14],设定所有旅客组的转换系数α(g)为1,表明实际出发时刻与期望值的偏差可等价视为在途时间;设定旅客对成本偏离最短路的容忍上限ε(g)为60;参考文献[15],高、中、低收入旅客组所对应的票价敏感系数βg分别为0.5、1和1.5;所有列车运载能力相同,为1 000;算法最大迭代次数H为400。

表3 参数设定表
4.2 结果分析
(1)实验结果
将上述参数带入模型进行求解,经400次迭代,耗时2.0 h,求得的上界、下界分别为1 204.25、1 077.93万元,误差率为10.49%,上、下界及误差率随迭代次数的变化曲线见图5、图6。算法的收敛效果良好,验证了算法的可行性。
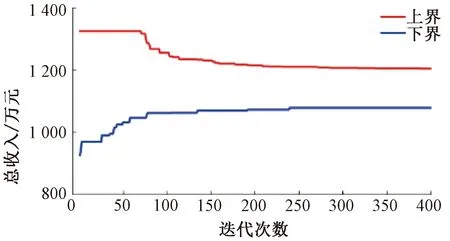
图5 上下界随迭代次数变化曲线
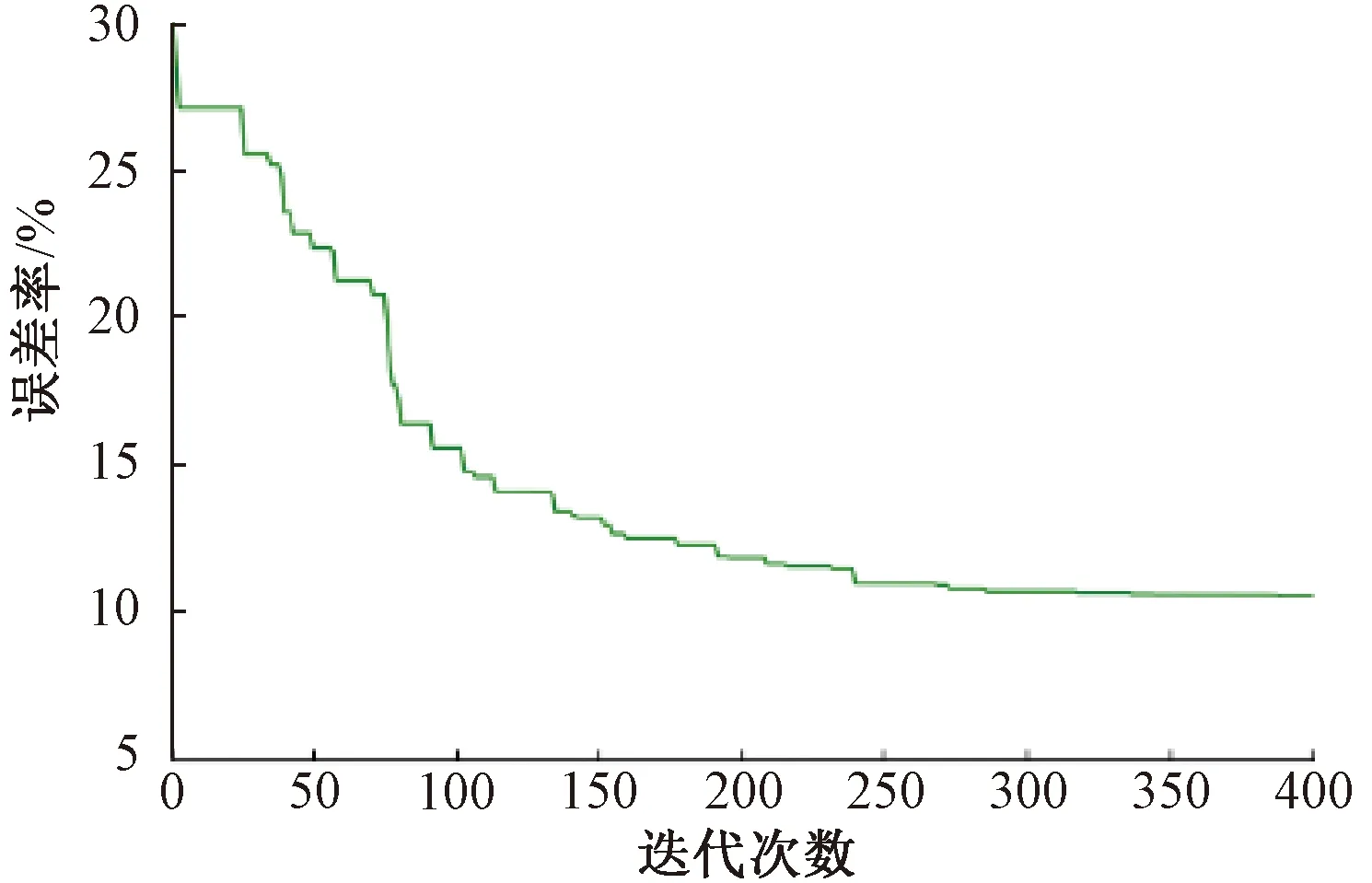
图6 误差率随迭代次数变化曲线
在客流低谷期发出列车的上座率见表4。由于列车能力不足和出行成本过高,部分旅客将流失,总的旅客流失数量为1 465人。

表4 低谷期列车的上座率
通过求解也能获得每列车在各服务OD间的票价方案。本文通过列出各列车所采取的不同票价策略的次数来反映票价的变化情况,见表5。在获得的可行解中,G103、G127、G129和G133等在大多在客流低谷期发出的列车在更多的OD间采取了折扣优惠票价策略,以降低旅客出行费用,从而吸引更多旅客乘坐高铁。特别地,由于列车G9停站次数较少,旅行时间短,使得其无需采用降价措施。此外,由于长距离OD的基础票价较高,在采取涨价策略后,涨幅较大,因此部分高峰期列车在长距离OD间也采取了降价措施,但均为折扣10%。
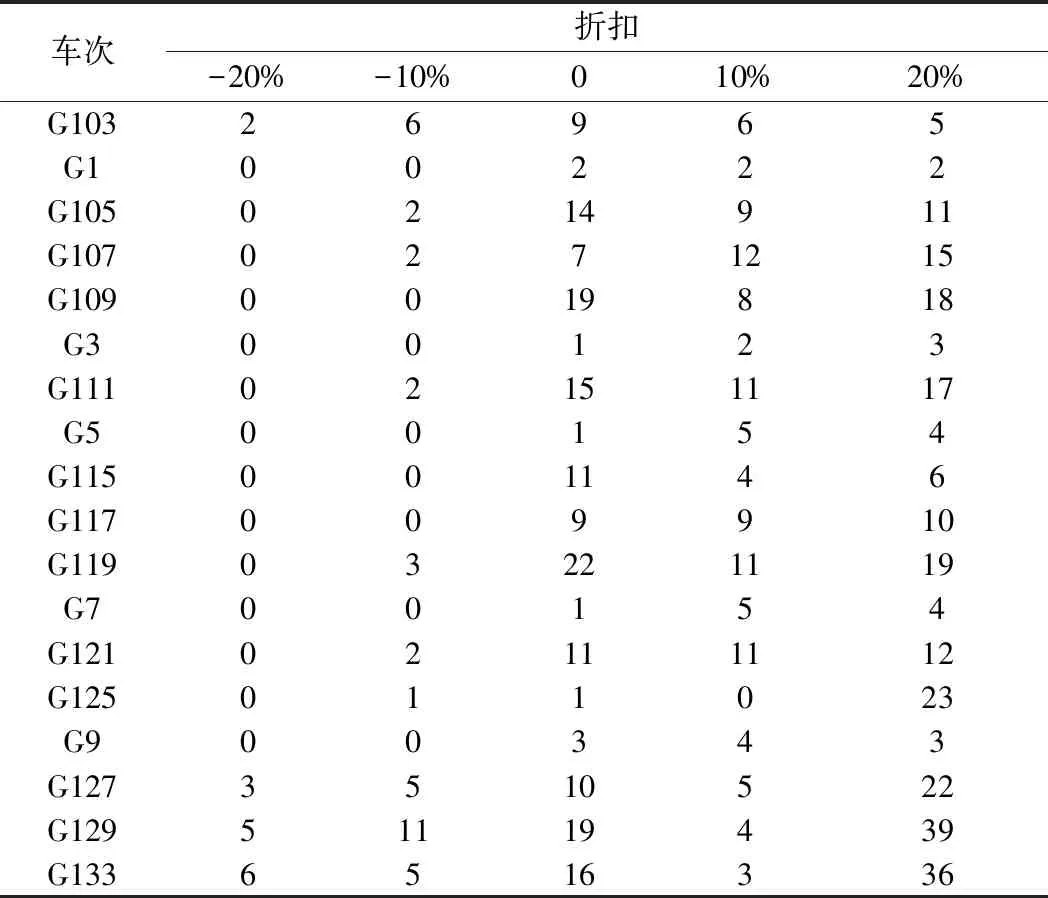
表5 各列车采取票价策略的次数
(2)两种票价策略对比分析
本文将价格等级改为N={3}(即始终维持原价),保持其他参数不变,进行第二组实验,以对比分析差异化票价策略与扁平化票价策略的差别。
在扁平化票价策略下,求得上界值为1 104.54万元,下界值为982.77万元,流失旅客数量为3 399人,见表6。由表6可见,与扁平化票价策略相比,差异化票价策略优势明显。在上界值提升的同时,所获得的可行解(下界值)也更优,总客票收入增加约95.16万元,提升9.68%。此外,流失旅客数量下降了1 934人,使得低谷期列车上座率得到提升,见图7。这说明合理制定列车票价可以吸引更多旅客乘坐高铁,从而达到“削峰填谷”的效果。需要说明的是,由于列车G127停站次数少,且G127、G129次列车发车间隔时间偏差小,导致在扁平化票价策略下G127吸引了部分G129的旅客。

表6 收入上、下界和流失旅客对比
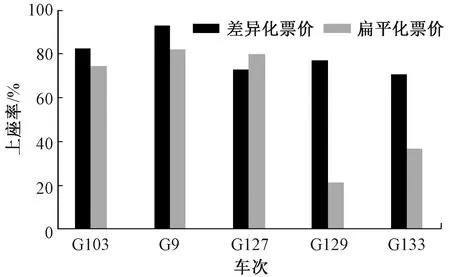
图7 低谷期列车上座率对比
4.3 灵敏度分析
(1)参数ε(g)
本文对参数ε(g)进行灵敏度分析。具体地,保持其他参数与4.1节一致,在此基础上,依次将ε(g)设定为20、40、80和100带入模型进行求解。实验结果见表7。
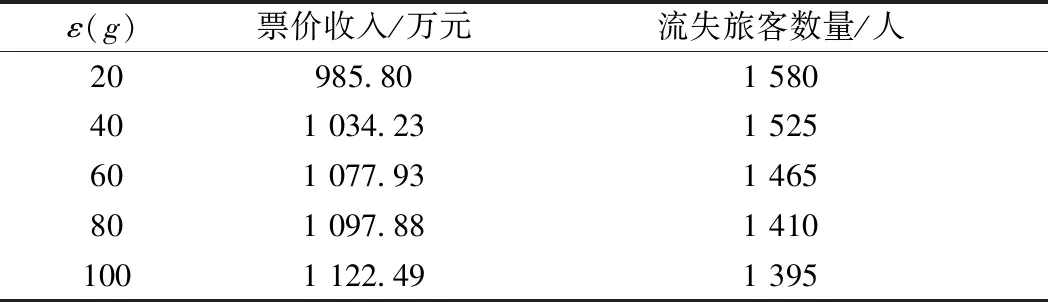
表7 参数ε(g)灵敏度分析结果
由表7可见,随着参数ε(g)的增长,旅客可承受的最高出行成本在上升,一方面更多OD的票价可上浮范围扩大,另一方面使得更多的旅客可乘坐低谷期列车,从而带来了旅客流失量的减少和总票价收入的提高。
(2)参数α(g)
本文分别设定参数α(g)为0.5和1.5,同时设定其他参数与4.1节一致(ε(g)=60),进行灵敏度分析,结果见表8。

表8 参数α(g)灵敏度分析结果
由表8可见,随着参数α(g)值的增长,旅客实际出发时间与期望值的偏差在总成本中的占比提高,从而导致在可承受最高出行成本一定的情况下,流失旅客数量变多,且总票价收入降低。
(3)票价策略
在此实验中,延续4.1节参数设定,但增加两种价格策略(降价30%和涨价30%),以测试模型算法的可行性和有效性,结果见表9。

表9 增加票价策略数量的求解结果
显然,由于票价可浮动范围扩大,高峰期列车可进一步提升票价,而低谷期列车则可在部分OD间采用大幅降价模式来吸引旅客,最终使得总票价收入上升和流失旅客数量下降。此外,票价策略个数增加,使得价格-时空网络中弧的数量增长,导致求解时间变长。
5 结论
(1)本文通过构建价格-时空三维网络,将高铁票价优化问题转化为多维网络中的客流分配问题。在此基础上,考虑旅客对价格敏感度的异质性,提出刻画旅客出行成本的效用表达式。最终,考虑列车能力限制、旅客有限理性选择、价格策略唯一性等约束,构建高铁票价整数线性规划模型,并提出基于拉格朗日松弛的求解算法。
(2)以京沪高铁为对象进行案例分析,验证了本文提出方法的可行性。实验结果表明,客流低谷期列车采用适当的票价折扣优惠策略能够降低流失旅客的数量,提高列车上座率,同时与固定票价策略相比,能够使总客票收入增加了9.68%。此外,对模型中的不同参数进行了灵敏度分析,验证了方法的有效性和合理性。
(3)未来可考虑票价在售票期内的动态调整,并改善价格-时空网络的构建思路和方法,以开展高铁动态定价研究,丰富和完善高铁票价优化理论与技术。
