基于扰动观测器的农用驱动电机变速滑模控制
2022-08-08涂群章蒋成明朱昌林涂志文
黄 皓 涂群章 蒋成明 潘 明 朱昌林 涂志文
(陆军工程大学野战工程学院, 南京 210007)
0 引言
近年来,永磁同步电机(Permanent magnet synchronous motor, PMSM)作为驱动电机已经成为电传动农用车辆发展的一个热点方向,为整车实现高效率、快响应、低污染的驱动起到了重要的作用[1-2]。然而, 由于PMSM为非线性、多耦合、变参数的复杂控制对象,其控制技术目前仍不成熟[3]。针对农用PMSM的控制,应用较为广泛的PI控制策略具有结构简单、控制方便等优点,但是传统的PI控制策略难以同时实现小超调量和快响应性,且PI控制策略的参数目前只能通过试错法获得,存在控制误差较大、响应速度不足、抗干扰能力差等缺点[4-6]。另一方面,由于农用PMSM在控制过程中,容易受到温度、磁场、振动等外界干扰因素影响,控制过程中存在内部机械参数摄动和外界负载波动等不良扰动,严重影响了PMSM的调速性能和控制精度,无法实现农用PMSM在电传动农用车辆上的高效率、高精度驱动[7]。
滑模控制(Sliding mode control, SMC)基于其对模型精准度要求不高、对控制参数变更不敏感、响应速度快等优点,可以较好地解决PI控制中存在的不足,成为国内外学者研究的热点。文献[8]提出了一种基于全局滑模控制和快速幂次趋近律的滑模控制算法,有效地解决了滑模控制中的抖振和干扰问题。文献[9]提出了一种基于自适应控制的滑模算法,有效地解决了建模中的耦合影响。文献[10]提出了一种基于积分型SMC的电机控制策略,该控制策略有效地提升PMSM的稳定性和响应速度,同时采用扰动观测器对外界负载进行补偿。文献[11]设计了一种模糊滑模控制对PMSM进行线性化处理,有效地减轻了控制器负担,提升了控制精度。文献[12]提出了一种基于扩展状态观测器的无传感器滑模控制,解决了负载扰动对PMSM的影响,且可解决在某些特殊场合中电机传感器安装复杂的问题。文献[13]提出了一种基于模型预测的滑模控制策略,用于解决PMSM建模困难,且参数容易发生时变的问题。文献[14]对PMSM中的过热退磁现象进行了热补偿,同时通过转矩滑模观测器对电机中转矩波动进行补偿。
上述的SMC策略可以有效提升电机的控制性能,但是在滑模控制过程中,由于都是采用传统的等速趋近率,控制过程会存在抖振过大、响应速度慢等缺点[15]。针对这一不足,设计一种基于变速趋近率的SMC进行改进。另外,针对PMSM内部机械参数摄动和外界负载扰动对调速造成的不良影响[16-17],采用变速滑模观测器对农用PMSM的内/外部扰动进行实时观测和补偿,抑制扰动参数对电机控制性能的影响。
1 PMSM数学模型建立
基于建模对象PMSM是一个非线性、强耦合、多变量的复杂控制系统,在不影响对主要问题的研究结果前提下,本文进行以下假设[18]:①研究对象为表贴式PMSM。②不考虑电机的谐波效应和磁路饱和。③不考虑转子上的阻尼。④不考虑电机的铁芯损耗,包括涡流损耗和铁磁材料带来的损耗等。
PMSM动力学方程为
(1)
式中Te——电机转矩
TL——负载扭矩
B——磁滞摩擦系数
ω——电机角速度
J——电机转动惯量
PMSM电磁转矩方程为
(2)
式中ψf——永磁体磁链
P——电机极对数
id、iq——d-q旋转坐标上电流
Ld、Lq——d-q旋转坐标上电感
由于研究对象为表贴式电机,有Ld=Lq,式(2)可化简为
(3)
PMSM在d-q坐标系下电压方程为
(4)
式中Rs——电机电阻
ud、uq——d-q旋转坐标上电压
搭建PMSM控制系统基本结构,其控制框图如图1所示。

图1 PMSM控制系统框图Fig.1 PMSM control system block diagram
2 PMSM调速系统设计
针对PMSM传统PI控制中存在的响应速度较慢、超调量大等不足之处,设计了滑模变结构控制对PMSM转速进行调控,并通过设计一种变速趋近率对传统滑模控制中的等速趋近率进行替代从而减少滑模抖振现象,提高PMSM控制系统响应速度[19]。
2.1 滑模控制器设计
PMSM状态变量为
(5)
式中ωe、ω为指令角速度和输出角速度,角速度ωe为常数量,x=[x1x2]T为状态变量,式(5)求微分可得
(6)
(7)
为了削弱系统状态变量和提高滑模控制趋近品质,选择线性滑模面作为滑模控制器,其表达式为
s1=cx1+x2
(8)
式中s1——基于等速趋近率的线性滑模面
c——滑模控制参数
通过采用等速趋近率可得滑模控制输出为

(9)
式中ε1——线性趋近参数
sgn(·)——符号函数
将式(8)代入式(9),可得
(10)
将式(7)代入式(10)可得
cx2+g(x)+f(x)-bu=-ε1sgn(s1)
(11)
简化式(11),可得状态系统的控制输出为
(12)

(13)
式中τ——采样时间
控制电流iq输入至电流控制器对PMSM进行控制。
2.2 变速趋近率设计
定义滑模运动切换带带宽为
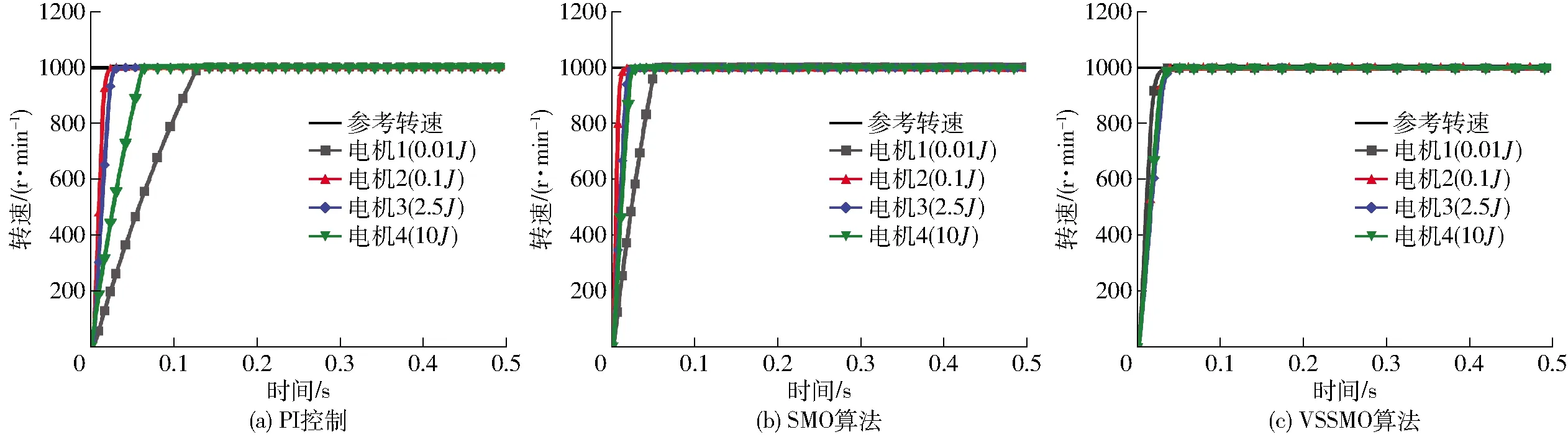
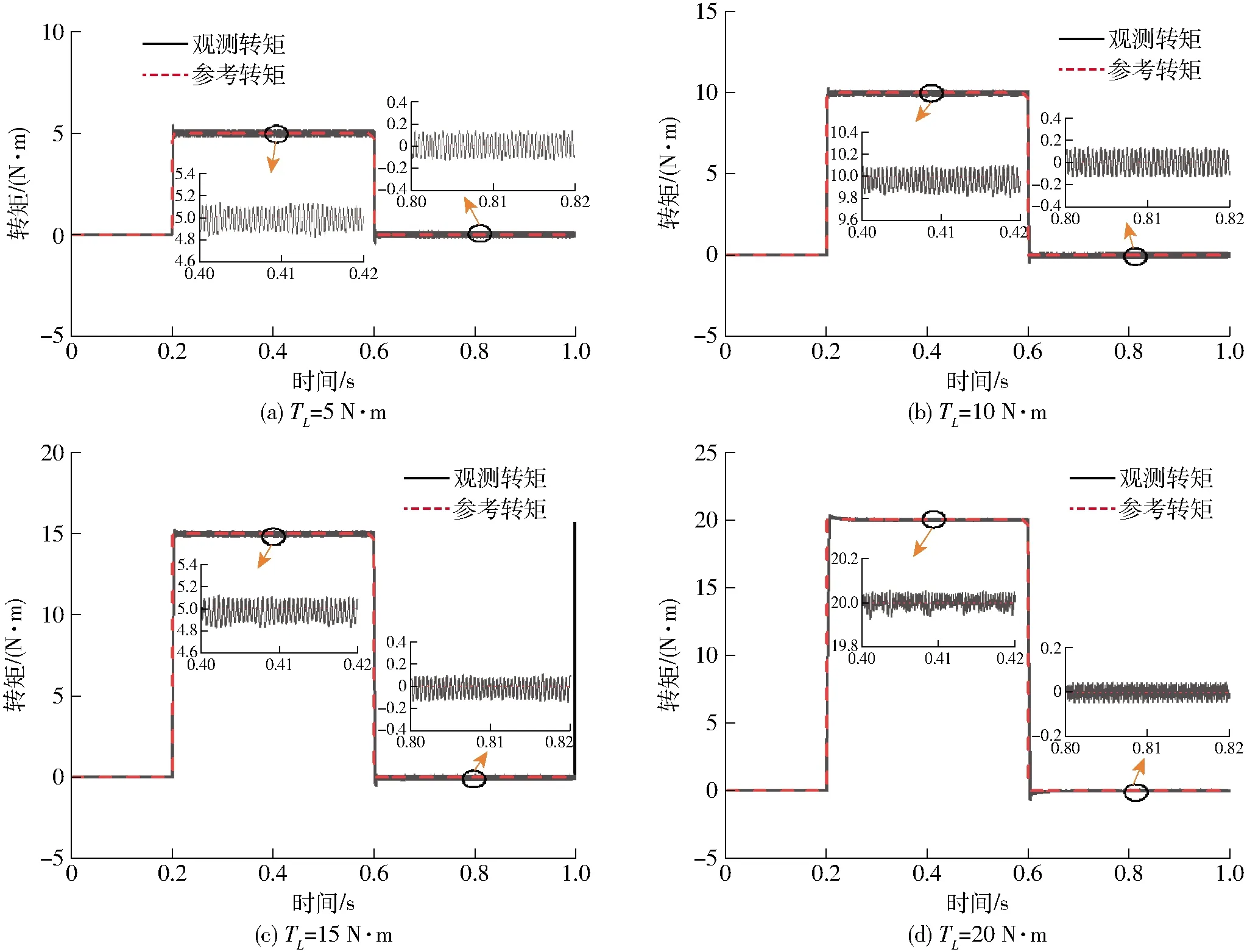
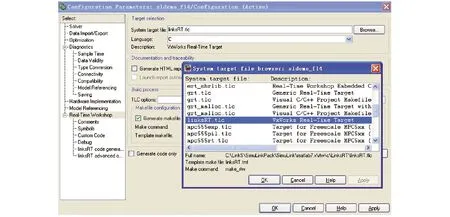
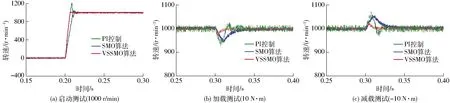
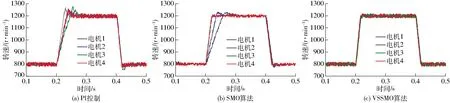
{x∈Rn|-Δ (14) 式中Δ——切换带带宽 由式(9)可得等速趋近率的离散形式为 s1(k+1)-s1(k)=d(s1(k))/dt=-ε1Tsgn(s1(k)) (15) 式中T——采样周期 由式(15)可得 (16) 式(16)说明,等速趋近率的切换区域带框是由将滑模切换面夹在中间的两条平行射线组成,切换面带宽为 Δ=ε1T (17) 由式(17)可得等速趋近率的切换面带宽是一个常数,这表明在等速趋近率的控制下,系统状态无法在有限时间内收敛到平衡点,同时会产生幅值为ε1T和-ε1T的抖振现象,且抖振值由采样周期决定,等速趋近率的相轨迹如图2所示。 图2 等速趋近率相轨迹Fig.2 Isokinetic approach rate phase trajectory 由于等速趋近率在控制过程中存在自身的缺点,即滑模运动时的切换带为带状,使得系统在切换带运动时始终无法到达平衡点,增加了控制器的负担[19-20]。另外,趋近速度和抖振仅取决于等速控制参数ε1,为了解决这一问题,引入了一种新型变速趋近率,其形式为 (18) 式中ε2——变速趋近率的比例控制参数 ‖x‖1——系统状态范数 s2——基于变速趋近率的线性滑模面 由式(18)可得变速趋近率的离散形式为 s2(k+1)-s2(k)=d(s2(k))/dt= (19) 对于变速趋近率,由式(19)可得 (20) 式(20)表明变速趋近率的切换带是经过原点的两条射线组成的扇形,并将滑模切换面s=0夹在中间,图3为变速趋近率相轨迹,其切换面带宽为 图3 变速趋近率相轨迹Fig.3 Variable speed approach rate phase trajectory Δ=ε2T‖x(k)‖1 (21) 由式(21)可知,变速趋近率的切换面带宽不仅与采样周期有关,还和系统状态范数成比例。当系统趋近稳态时,系统范数将趋近于0,此时可以使得系统具有较好的稳态性能。 在基于变速趋近率的PMSM滑模控制器的基础上,通过对转速跟踪误差进行稳定性分析,判断是否有界,其判断过程如下: 构建基于变速趋近率滑模控制下转速追踪误差的Lyapunov方程,其表达式为 (22) 式中滑模面s2为包含转速追踪误差及其微分的滑模面,通过对滑模面s2的稳定性分析,可以证明PMSM转速追踪误差的有界性。 (23) 综上可得,采用基于变速趋近率的滑模控制策略可以较好地解决传统滑模控制中等速趋近率抖振较大的问题,可以较好地解决PMSM滑模控制过程中的趋近误差。将变速趋近率式(18)代入式(13),可得PMSM在基于变速趋近率的滑模控制策略下的电流控制方程为 (24) 农用PMSM的转速会受到内部参数中转动惯量J、磁滞摩擦系数B、负载扭矩TL的直接影响[21]。传统PI速度控制器只能调节电机的控制参数,无法对这些内部参数摄动以及外界负载波动、扰动进行实时的调节和补偿,这些内部参数会直接影响到农用PMSM输出转速[22-23]。因此,需要采用合适的扰动观测和补偿控制策略对农用PMSM运行过程中的内部参数摄动和外界负载波动进行实时的观测和有效的补偿。 为了能够实现在线实时估计系统扰动,提出了一种扩展滑模扰动观测器,对PMSM控制过程中存在的扰动现象进行有效地抑制,由PMSM的动力学方程可得 (25) 在考虑外界载荷TL和PMSM内部参数影响下,式(25)可表示为 (26) 其中 式中an、bn、cn——常量参数 Δa、Δb、Δc——扰动参数 r(t)——扰动总和,其中包括内部参数中的转动惯量J、磁滞摩擦系数B、永磁体磁链ψf和外界负载扰动TL 假设系统中扰动r(t)满足以下限制 |r(t)|≤l (27) 式中l——系统扰动边界值 根据式(26)所示的PMSM变量动态方程,并定义PMSM的系统扰动量作为扩展状态观察变量,可扩展为 (28) 式中d(t)——扰动量变化率 由式(28)所示的PMSM动态拓展方程,可构建扰动的扩展滑模观测器为 (29) D——滑模控制参数 usmo——滑模开关函数 开关函数的表达式为 usmo=ηsgn(S) (30) 其中 S=e1=-ω 式中η——滑模面切换参数 S——滑模切换面 构建扩展滑模观测器的结构框图如图4所示,对滑模面求微分可得 图4 扩展滑模观测器的结构框图Fig.4 Structure block diagram of extended sliding mode observer (31) 将式(28)代入式(31),化简得 (32) 将式(29)减去式(28)可得滑模观测器的误差方程为 (33) 其中 (34) 式中e1、e2——角速度和扰动估计误差 由Lyapunov函数稳定性判定条件,可得扩展滑模观测器方程需满足 (35) 由式(30)可得,S与滑模观测器中转速跟踪误差e1相等,当式(35)成立时,可以证明滑模观测器中的转速跟踪误差有界,将式(33)代入式(35),可得 (36) 分析式(36)可得,滑模面切换参数需满足 η≤-|e2-cne1| (37) 为了易于扩展滑模观测器模型搭建,定义 η=-M|e2-cne1| (38) 式中M——切换面安全控制系数,取2 综上可得,当定义切换面安全控制系数M,且滑模面切换参数满足式(38)时,基于扩展滑模观测器中的转速跟踪误差稳定且滑动模态可达,同时可以证明扩展滑模观测器有界。 在完成对扩展滑模观测器的稳定性参数设定后,此时系统状态可到达滑模切换面上时,可得 (39) 将式(33)代入式(39),可得 (40) 式(40)可简化为 (41) 求解式(41)可得 (42) 式中C为常数。且仅当滑模控制参数g>0时,扰动观测误差e2可以在有限时间内趋近为0,同时g的取值直接决定扰动观测误差e2趋近到0的收敛时间。 综上可得,当滑模面切换参数η和滑模控制参数g满足上述条件时,可以证明系统状态能够在有限时间内趋近到平衡点,且收敛速度与以上参数直接相关。 以PMSM的滑模观测器作为控制对象,其控制框图如图5所示。 图5 PMSM滑模观测器控制框图Fig.5 Block diagram of PMSM sliding mode observer control 对滑模观测器进行设计,其步骤如下: (1)状态变量定义 对PMSM的转速进行滑模控制,定义状态变量为 (43) (2) 滑模面选取 选择线性滑模面对扩展滑模观测器进行控制,其表达式为 S1=x1=ωe-ω (44) 对滑模观测器的线性滑模面求微分可得 (45) 将式(33)代入式(45),可得 (46) (3)滑模趋近率设定 通过采用变速趋近率[24],可得滑模控制输出为 (47) 将式(46)代入式(47),可得 (48) 化简式(48)可得 (49) PMSM在基于变速趋近率的滑模控制下的复合控制框图如图6所示。 图6 PMSM复合控制框图Fig.6 PMSM composite control block diagram (4)变速滑模观测器系统稳定性分析 为了证明变速滑模观测器的稳定性,并判断其是否有界,构造滑模观测器的Lyapunov函数为 (50) 根据Lyapunov函数稳定性判断标准,可得 (51) 将式(47)代入式(51)可得 (52) 由上述推导公式可以判定系统稳定且滑动模态可达。 为了验证本文提出的PMSM基于变速趋近率(Variable speed rate)的滑模观测器(Sliding mode observer, SMO)(简称为VSSMO)对于参数补偿效果的有效性,将无滑模观测器的PI控制策略[25],传统滑模观测器[26]与本文提出的基于VSSMO抗扰动技术进行仿真测试对比。同时,通过搭建的4个电机测试平台,给定各电机不同的机械参数和负载扭矩进行实验测试,验证控制策略的有效性。 为了验证本文提出的VSSMO的控制性能,对多电机控制系统Simulink仿真模型中各电机设定不同的机械参数和外界负载,观察在这些参数设定下各电机的转速仿真测试结果,并将本文提出的VSSMO与SMO和无观测器的传统PI控制策略进行对比。图7为多电机控制平台中各电机设定不同的转动惯量J时,其他参数不变,接收到转速为1 000 r/min启动指令下仿真测试结果;图8为设定不同的磁滞摩擦系数B时的启动仿真测试结果;图9、10分别为多电机控制平台中各电机收到不同的加载/减载指令时,该电机平台的转速仿真测试结果;图11为扩展滑模观测器负载转矩观测仿真测试结果。 图7 不同转动惯量J下多电机启动仿真测试结果Fig.7 Simulation test of multi-motor starting under different moments of inertia J 图8 不同磁滞摩擦系数B下多电机启动仿真测试结果Fig.8 Simulation test of multi-motor starting under different moments of friction coefficient B 图9 多电机控制平台突增负载仿真测试结果Fig.9 Simulation test of sudden load increase on multi-motor control platform 图10 多电机控制平台突减负载仿真测试结果Fig.10 Simulation test of sudden load decrease on multi-motor control platform 图11 不同负载转矩TL参数鲁棒观测值Fig.11 Robust observed values of torque parameters under different loads TL 如图7和图8所示,当多电机控制平台中的各电机设定不同的机械参数时,如图7a和图8a所示的传统PI控制策略由于无法实现对机械参数的有效观测和补偿,导致各电机在启动过程中,转速响应曲线偏差性较大,且电机1完成启动响应消耗的时间较长,这在实际控制过程中会对多电机协同控制造成较大的控制误差。相较传统PI控制策略,图7b和图8b的仿真结果中由于引入了SMO对PMSM中的机械参数进行有效地观测和补偿,使得各电机之间的转速误差较传统PI控制策略有较大程度的削减。但由于传统SMO中趋近速度较慢,且在控制过程中抖振现象会影响到观测误差,导致各电机之间仍然存在一定的追踪误差。图7c和图8c为基于VSSMO下的多电机控制平台转速仿真测试,由该测试结果可以看出,通过VSSMO对磁滞摩擦系数B和转动惯量J高精度的观测和补偿,使得各电机可以较好地实现误差较小的协同控制,控制误差较小。 图9和图10为多电机控制仿真平台受到突增负载和突减负载时,且各电机受到的负载不同时,基于VSSMO、SMO和PI控制策略各电机的转速仿真测试曲线。由图9c和图10c可得,当施加不同的加载和减载时,各电机在本文提出的基于VSSMO的控制策略下转速追踪误差较小,最大追踪误差可以控制在10 r/min之内;相较VSSMO,基于传统SMO的多电机控制平台加载和减载时,各电机之间的最大追踪误差提升至VSSMO的2倍以上,如图9b和图10b所示;而传统PI控制策略由于没有参数观测器,当四电机控制平台中各电机受到的外界载荷不同时,各电机之间转速追踪误差较大,最大误差超过60 r/min,如图9a和图10a所示。 由上述仿真加载/减载测试结果可得,通过本文提出的基于VSSMO抗扰动控制策略,可以对PMSM的附加载荷实时观测并补偿,使得各电机处于负载转矩不一致工况下也可保持较小的转速误差,较好地解决了电机受外界负载的转速波动影响。 为了证明提出的扩展滑模观测器对外界负载TL的观测效果,对永磁轮毂电机进行不同的加载工况并观察其仿真结果。具体仿真工况为0.2 s时给永磁轮毂电机施加一个突增负载,在0.6 s时将施加的负载突减到0,其突增的负载分别为5、10、15、20 N·m,由本文设计的观测器对其进行观测,由图11的负载扰动鲁棒观测值可得,当对永磁轮毂电机施加不同的附加载荷TL时,通过本文设计的鲁棒观测器,可实现对负载扰动的实时观测。当达到稳态观测值时,观测误差可以控制在0.2 N·m之内,且观测过程几乎为同步追踪,具有较好的观测精度。 为了进一步验证本文提出的抗扰动技术,依托搭建的多电机调速系统控制平台进行实验,如图12所示。 图12 多电机调速系统控制平台Fig.12 Control platform of multi-motor speed regulation system 控制柜中伺服电机DSP控制板的开发过程中,包含硬件、嵌入式软件和控制算法的调试。本实验平台在设计过程中,直接将Simulink模型自动生成C语言控制源码,再由CCS软件和DSP仿真器将C语言源码烧写到DSP板卡中执行,图13为代码编译器截图。在Simulink控制模型中,采用M语言来描述算法逻辑部分,展示了仿真用的 M 语言代码与自动生成的DSP控制源码对比,图14为模型中M语言和生成C代码对照。 图13 代码编译器Fig.13 Code compiler 图14 M语言与生成的C代码对照Fig.14 Comparison between M language and generated C code 基于该多电机调速系统控制平台中惯量盘(图15),可以通过惯量盘对电机转动惯量进行调整,实验中对多电机平台中各电机调整的转动惯量分别为J、2J、5J、10J,各自对应多电机平台中的电机1~4,基于该设定下,进行多电机启动、多电机变速和多电机加载实验,并将本文提出的基于VSSMO的抗扰动控制策略和基于传统SMO抗扰动策略以及无扰动观测器的PI控制技术进行对比,电机策略转速和转矩由Kistler传感器进行采集,采样频率为10 kHz,如图16所示。其中,同一电机的启动、加载、减载实验测试如图17所示,多电机调速系统控制平台的启动、变速和不同变量下的加载实验结果如图18~21所示。 图15 电机惯量盘组实物Fig.15 Motor inertia group 图16 Kistler传感器实物Fig.16 Kistler sensor 图17 不同控制策略下单电机性能实验测试结果Fig.17 Performance test of single motor with different control strategies 图18 多电机调速系统控制平台启动实验测试结果Fig.18 Starting test of control platform of multi-motor speed regulation system 由图17a可知,永磁轮毂电机收到转速1 000 r/min启动指令时,本文提出的VSSMO算法可在100 ms之内完成启动指令,达到平衡点,且在启动状态下无超调现象。相比较本文提出的控制策略,传统SMO算法和PI控制策略在启动时都存在超调现象,并且PI控制策略超调现象十分严重,最大波动值超过20%。同时,本文提出的VSSMO算法在启动时的转速曲线十分平滑,达到指令速度后转速波动较小。通过实验平台的启动测试,证明了本文基于VSSMO算法的速度控制器具有较好的启动性能和稳定性。图17b、17c为电机控制平台在1 000 r/min转速指令下稳定运行时,接收到10 N·m加载指令和-10 N·m的减载指令的实验测试结果。由实验结果可得,PI控制策略在加载时转速波动较大,且在调节过程中存在较大幅度的转速超调波动,传统SMO策略在控制过程中无超调现象,但是调节时的转速波动超过本文提出的VSSMO策略的2倍。本文提出的VSSMO策略抗干扰能力较强,收到负载时的转速波动可控制在5%之内,调节速度较快,能在0.15 s之内调节转速至稳态。通过上述加载/减载实验可得,本文提出的速度控制策略,具有较好的抗干扰能力和鲁棒性。 由图18可知,当连接不同的惯量盘,对多电机调速系统控制平台中的各电机设定不同的转动惯量时,无扰动观测器的传统PI控制在启动时各电机之间存在较大的转速误差,且在控制过程电机响应速度较慢且存在超调,如图18a所示。基于SMO的PMSM抗扰动控制技术中各电机之间的转速误差相较PI控制明显减少,但在控制过程中仍然有一定的超调,如图18b所示。本文提出的基于VSSMO的电机抗扰动控制,如图18c所示,由于其趋近速度快且滑模控制过程中抖振较小,使得该控制技术的各电机转速误差由于前两种控制策略,且在电机控制过程中几乎无超调现象,在启动响应时体现了较好的追踪性能和稳定性。 由图19可得,本文提出的基于VSSMO的电机抗扰动控制技术在电机加速/减速时均可实现各电机之间的较好的转速追踪,且在控制过程中响应速度较快,各电机在控制过程中无超调现象,响应性能相较前两种控制策略有明显的提升。 图19 多电机调速系统控制平台变速实验测试结果Fig.19 Variable test of control platform of multi-motor speed regulation system 由图20可得,基于VSSMO的电机抗扰动控制技术可在施加相同载荷时,在各电机转动惯量不同的情况下通过对转动惯量进行补偿实现多电机的协同控制。传统PI控制策略在无扰动观测器进行机械参数补偿情况下,转矩对各电机产生的转速波动有较大的差异。基于SMO的电机抗扰动技术,由于其趋近速度较慢且趋近过程中抖振误差较大,导致各电机的转速追踪性能相较本文提出的抗扰动技术存在明显不足,且响应时间较长。 图20 多电机调速系统控制平台加载实验测试结果Fig.20 Loading test of multi-motor speed regulation system 图21为当多电机调速系统控制平台收到不同负载指令时的各电机转速实验测试结果。在该加载测试中,各电机机械参数均设定为相同,电机1~电机4接收的负载分别为30、20、10、0 N·m时,基于VSSMO、SMO和PI控制3种控制策略下进行各电机的实验测试。本文提出的基于VSSMO的PMSM抗干扰策略可以使得各电机之间的转速最大误差控制在5%之内,且各电机可以在0.1 s左右恢复至转速稳定点。无扰动观测器的PI控制策略各电机之间转速追踪误差较大,最大误差超过150 r/min。基于SMO的电机抗扰动策略实验测试结果,由该实验结果可以发现其对电机的变转矩观测和补偿效果明显不如本文提出的基于VSSMO抗扰动策略,主要存在各电机之间转速误差较大且调节时间较长等缺陷。 图21 不同负载下多电机调速系统控制平台加载实验测试结果Fig.21 Loading test of multi-motor speed regulation system under different torque values (1)针对PMSM在控制过程中存在的扰动问题,且阐述了电机收到的外界负载扰动以及内部机械参数摄动对其控制性能的影响。在此基础上,结合PMSM的数学模型,提出了一种基于变速趋近率的滑模控制策略,提升PMSM的控制性能和减少抖振波动。为了抑制PMSM控制过程中的内部机械参数和外界负载扰动,选扩展滑模观测器对其进行观测和补偿。在设计滑模观测器的过程中,分析了传统滑模观测器中存在趋近速度慢、抖振较大等问题,选取了基于变速趋近率的滑模观测器进行替代,并构建Lyapunov函数证明了其稳定性。 (2)通过Matlab/Simulink联合仿真测试和多电机调速系统控制平台的实验验证,证明了通过设计的VSSMO算法,可以有效地抑制电机的内部机械参数和外界负载对其的转速干扰,可以有效地弥补农业电传动车辆中电机参数发生时变带来的不良影响,提升整车的可靠性和抗干扰能力。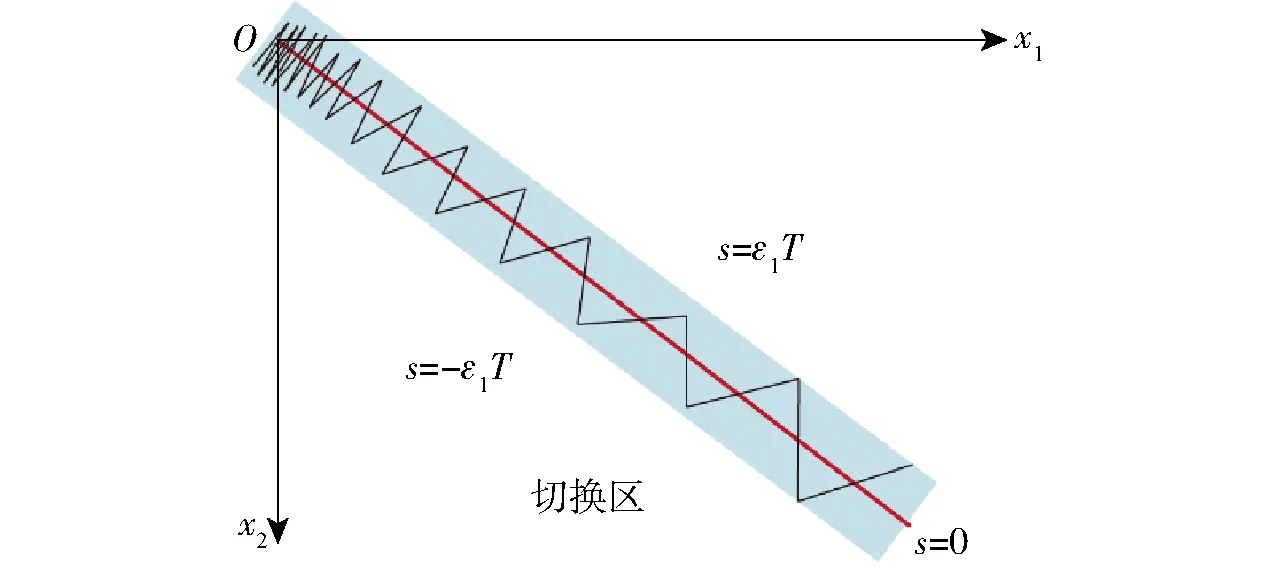
-ε2T‖x(k)‖1sgn(s2(k))
2.3 系统跟踪误差稳定性
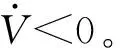
3 基于滑模观测器的抗扰动技术
3.1 扩展滑模观测器设计
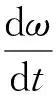


3.2 扩展滑模观测器稳定性分析及参数选择

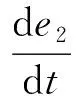
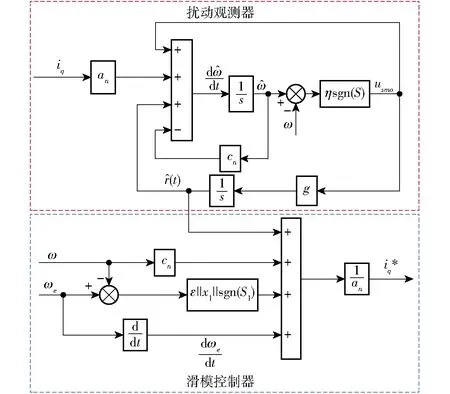
3.3 基于变速趋近率的滑模观测器设计

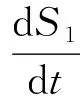


4 仿真与实验
4.1 仿真分析


4.2 实验测试







5 结论
