主被动闭环融合调姿隔振平台动力学建模与模态分析
2022-08-08耿明超赵铁石李二伟陈宇航王占英
耿明超 赵铁石 李二伟 陈宇航 马 宏 王占英
(1.河北建筑工程学院机械工程学院, 张家口 075000;2.燕山大学河北省并联机器人与机电系统实验室, 秦皇岛 066004;3.北华航天工业学院机电工程学院, 廊坊 065000)
0 引言
载体的扰动频率跨越了高、中、低多个频段,而单一类型作动器只能解决特定频段和幅值范围内的问题,即现有的机构一般只能实现单一的调姿或者隔振功能。大幅度位姿补偿一般是通过稳定平台实现。KOLECKI等[1]基于Stewart机构研制了一种轻型稳定平台用于稳定激光扫描仪,电动缸驱动。刘晓等[2]研制了6-PUS的舰载稳定平台,通过伺服电机和丝杠驱动滑块运动。ZHANG等[3]研制了具有3个转动自由度的稳定平台。于荣荣等[4]基于3-RPS机构,通过电机驱动液压缸伸缩实现目标调姿。稳定平台的作动器多为行程大但频率响应较低的电动缸、液压缸等。
隔振技术根据对振动的补偿原理可分为被动式、主动式和主被动混合式[5]。于大国等[6]将并联机构的驱动替换为弹性阻尼装置,实现了多维减振。牛军川等[7]在选定的主动副处安装相应的弹簧阻尼装置建立了多维隔振平台。对于中高频振动而言,被动性隔振方式具有良好的隔振效果,但对于低频振动往往难以有效地控制,负刚度的引入虽然能够降低系统的固有频率,但高效紧凑的负刚度结构实现难度较大,制约了其应用[8-10]。LIU等[11]以音圈电机为作动器,构建了八分支的并联机构来隔离空间站的振动。王兵[12]通过控制音圈电机实现并联平台的调姿与隔振。李耀等[13]搭建了基于压电陶瓷的主动隔振系统。由于作动器带宽限制,主动隔振的性能主要集中在低频,主被动隔振技术则能够充分利用两者的优点,提供较宽频带的隔振[14-16]。LIN等[17]研制的隔振平台通过音圈电机来隔离低频振动,通过分支中的弹簧对中高频振动进行被动隔离。JANG等[18]研制了基于空气弹簧和压电堆作动器的主被动隔振平台。张洋[19]研制了基于压电陶瓷和粘弹性材料的六自由度主被动隔振平台。LI等[20]构建了五自由度混联式主被动隔振平台。主动、主被动隔振平台中,其作动器响应快,但行程小,如音圈电机为毫米级输出,而压电作动器、超磁致伸缩作动器仅为微米级输出,难以对大幅度位姿扰动进行补偿。
在真实工况下,位姿扰动与中高频振动一般是同时存在的,将稳定平台与隔振平台串联构成双层结构,能够同时实现多维的调姿与隔振,但会引发体积庞大、结构复杂、动态特性差等问题。张英等[21]构造了能够补偿大幅度位姿扰动的隔振平台,但电动缸串联弹性阻尼单元的形式增加了传动支链的长度。
针对补偿大幅度位姿扰动和隔离中高频振动一体化的需求,本文将驱动分支中的电动缸、液压缸等大行程作动器和弹性阻尼装置组成闭环子链,构成主被动闭环融合的并联调姿隔振平台。基于旋量代数建立这类包含闭环子链并联机构的运动学、动力学模型,并对其模态进行理论和实验研究。
1 调姿隔振平台构型描述
如图1所示,调姿隔振平台由动平台、定平台和3个相同的(P1RRP2R)RS分支组成,3个分支对称分布。R、Pi、S分别表示转动副、移动副和球副,下角标i表示移动副的顺序。

图1 调姿隔振平台机构简图Fig.1 Schematic of orientation adjustment and vibration isolation platform
闭环子链(P1RRP2R)为平面五杆机构。移动副P1上设置有弹簧阻尼装置,用以对外部的高频振动进行被动隔离。移动副P2以电动缸的形式实现,对外部的低频位姿扰动进行补偿。主动调姿、被动隔振单元分别位于五杆机构输出杆件aiei的两侧,以闭环子链的形式融合,能够有效减小传动支链的长度,降低机构的整体高度,改善机构动态特性。
在机构的定、动平台上各建立一个坐标系,定坐标系Oxyz原点O位于定平台的中心,x轴和Od1重合,y轴在定平台平面内与x轴垂直,z轴垂直定平台向上。动坐标系pxyz固连于动平台,其原点位于动平台的中心,在初始位置时方位与定系重合。并联调姿隔振平台的分支是以RRS分支为基础的,因此其自由度特性和3-RRS并联机构相同,具有两个转动和一个移动,但在每个自由度上有两个可动度。
2 调姿隔振平台运动学建模
2.1 分支描述
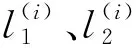
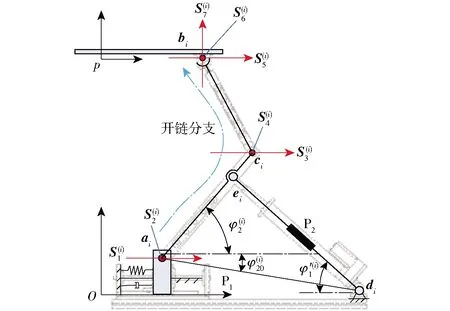
图2 调姿隔振平台分支机构简图Fig.2 Schematic of limb of orientation adjustment and vibration isolation platform
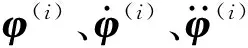
开链分支的运动旋量在定系中表示为
其中e1=(1,0,0)e2=(0,1,0)e3=(0,0,1)
式中aix、aiy——铰链点ai在定系x、y轴坐标分量
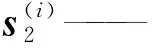
2.2 闭环子链运动特性分析



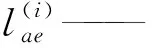
(1)
(2)
其中
(3)
其中
式中I3×3——3×3的单位矩阵
O3×3——3×3的零矩阵
(4)
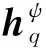
2.3 动平台一阶影响系数
动平台旋量速度可以表示为
(5)
其中
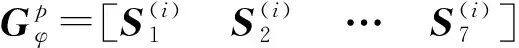

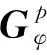

(6)
其中
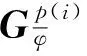
(7)
应用虚设机构法,得到机构的广义速度为
(8)
其中
根据式(8)机构动平台旋量速度表示为
(9)
式(9)可以进一步整理为
(10)
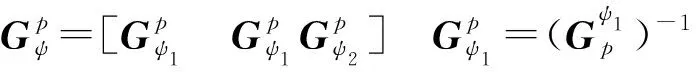
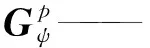
将式(3)代入式(10)中可得
(11)
其中

将式(10)代入式(7)可得到第i个开链分支的关节速度为
(12)
式(12)右边第2项是6×1的列向量,可将其表示为6×9的矩阵形式。对第1开链分支而言,式(12)可以表示为
(13)
其中
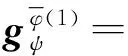
式中O——6×1的零向量
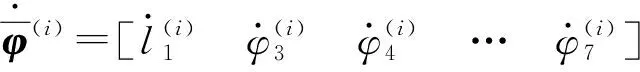
因此,第1开链分支关节速度可以表示为
(14)
将式(3)代入式(14)可得
(15)
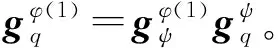
2.4 动平台二阶影响系数
对式(5)求导可以得到动平台旋量加速度与分支关节速度、加速度之间的关系
(16)
式(16)可进一步表示为
(17)

(18)
根据式(18),由虚设机构法构造广义加速度
(19)
其中
“*”表示矩阵的广义标量积。式(19)可以进一步整理为
(20)

动平台旋量加速度可表示为
(21)
其中
将式(3)、(4)代入式(21)可得
(22)
其中
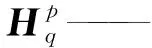
2.5 开链分支P1RRRS的一、二阶影响系数
将式(21)代入式(17)可得开链分支的关节加速度为
(23)
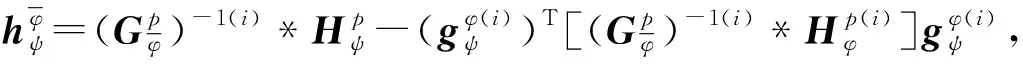
(24)
将式(3)、(4)代入式(24)可得
(25)
其中
则第i个开链分支第k个杆件的旋量速度、加速度可以表示为[23]
(26)

2.6 电动缸分支的一、二阶影响系数

(27)
(28)
式中f′1(i)、f′2(i)、f′11(i)、f′12(i)、f′21(i)、f′22(i)为函数f′(i)对两个变量的一阶、二阶偏微分,和式(1)、(2)中的符号物理意义一致。
电动缸分支关节速度与广义速度的映射可以表示为
(29)
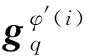
对式(29)求导可得
(30)
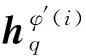
则电动缸分支第k个杆件的旋量速度、加速度表示为[23]
(31)

3 调姿隔振平台动力学建模
3.1 惯性力映射
(32)
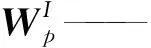
结合刚体旋量形式的牛顿-欧拉公式[23],式(32)可表示为
(33)
其中
式中Np——动平台的六维惯性矩阵
Io——动平台3×3的转动惯量在定系O中的表示
Ip——动平台转动惯量在质心坐标系的表示
pop——动系p相对定系O的位置矢量
mp——动平台质量

由文献[23]可知,式(33)可以表示为
(34)
其中
式中HRp——9×9×9的立方阵
立方阵HRp的第j层元素可以表示为
同理,机构中第i个分支,第k个杆件的惯性力产生的主动关节驱动力为
(35)
因此,并联机构动平台和所有分支杆件惯性力产生的主动关节驱动力为
(36)
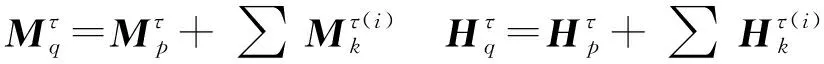
3.2 动力学模型
忽略摩擦,根据虚功原理,机构所有的外力处于平衡状态,则并联机构的动力学平衡方程为
τI+τG+τE+τF+τA=O
(37)
式中τG——机构的重力产生的广义驱动力
τE——作用在移动副P1上的弹性力
τF——作用在动平台外力产生的广义驱动力
τA——机构的广义驱动力
并联机构动平台及所有杆件的重力产生的广义驱动力为
(38)
作用在移动副P1上的弹性力为
τE=(τe,O6×1)
(39)
其中
式中ki——第i个分支中弹簧刚度
Fi——第i个分支中弹簧预紧力
并联机构动平台所受外力产生的广义驱动力可表示为
(40)
将式(36)、(38)~(40)代入式(37)可得机构在关节空间表示中的动力学模型为
(41)
关节变量q前3个元素表示被动隔振输入副P1,中间3个元素表示虚设运动副,后3个元素表示主动输入副P2,式(41)按照主、被动关节分解为
(42)
式中τu——被动隔振输入副P1的驱动力
τv——虚设运动副受到的力矩
τa——输入副P2的驱动力
由于是被动隔振,驱动力τu始终为零。虚设运动副受到的力矩τv由结构承担。驱动力τa为电动缸的主动输入。
由于虚设运动副的位移、速度、加速度始终为零,式(42)的第1行可表示为
(43)
式(43)为机构的动力学约束方程。当给定主动输入副P2的运动后,可以通过动力学约束方程求解得到被动副P1的加速度,一次积分得到速度,再次积分得到其位移。
3.3 动力学数值算例
为了验证上述运动学及动力学建模的正确性,对调姿隔振平台进行数值算例验证。调姿隔振平台的运动学、动力学参数如表1、2所示。

表1 运动学相关结构参数Tab.1 Structural parameters related to kinematics m
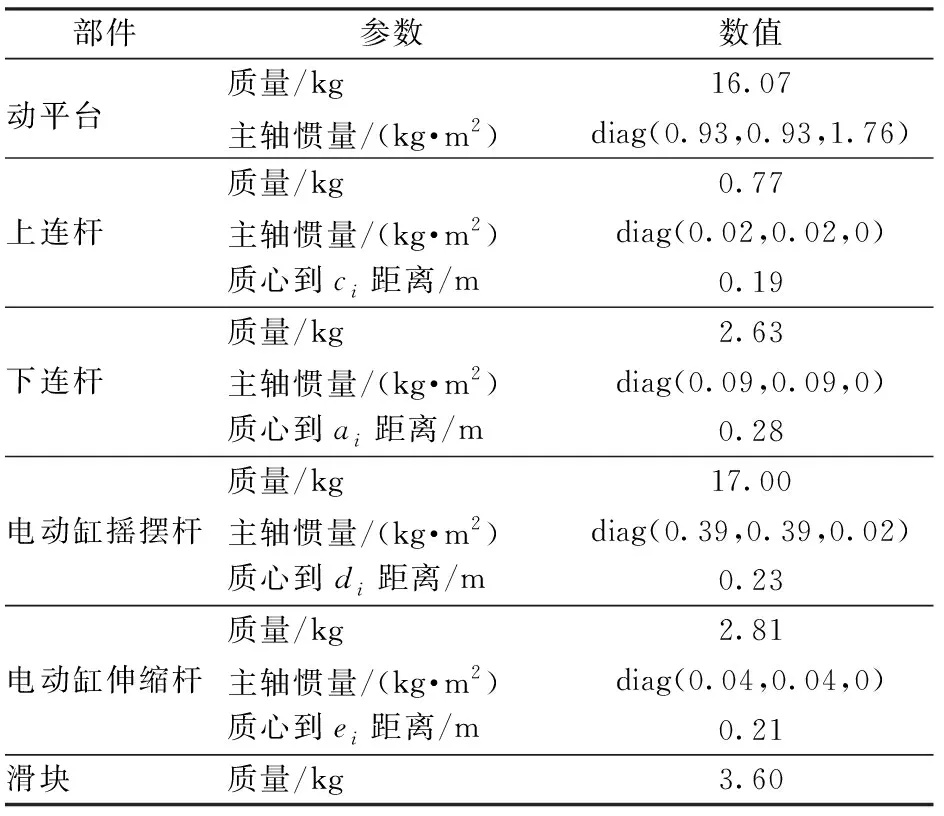
表2 动力学相关结构参数Tab.2 Structural parameters related to dynamics
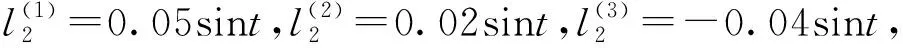
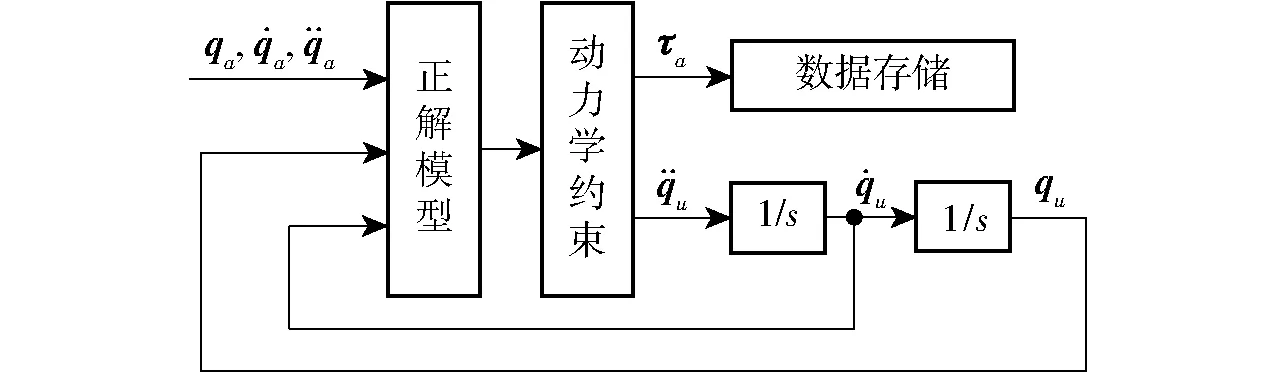
图3 动力学求解的Simulink模型Fig.3 Simulink model for solving dynamics
通过Simulink模型求解得到的关节驱动力曲线如图4所示。图5为ADAMS软件的仿真结果。图6为理论计算值和软件仿真值的偏差曲线,eτ表示关节驱动力τa理论计算值和软件仿真值的偏差。图5中软件仿真曲线在初始阶段存在一个微小波动,这是由于弹簧的预紧力不能和机构重力完全抵消造成的,但曲线整体趋势和图4的理论计算曲线一致。从图6可以看出,当系统稳定后,偏差范围在10-2量级,说明了上述运动学、动力学模型的正确性,也为后续的模态分析提供了理论基础。

图4 关节驱动力理论计算值Fig.4 Theoretical calculation value of joint driving force
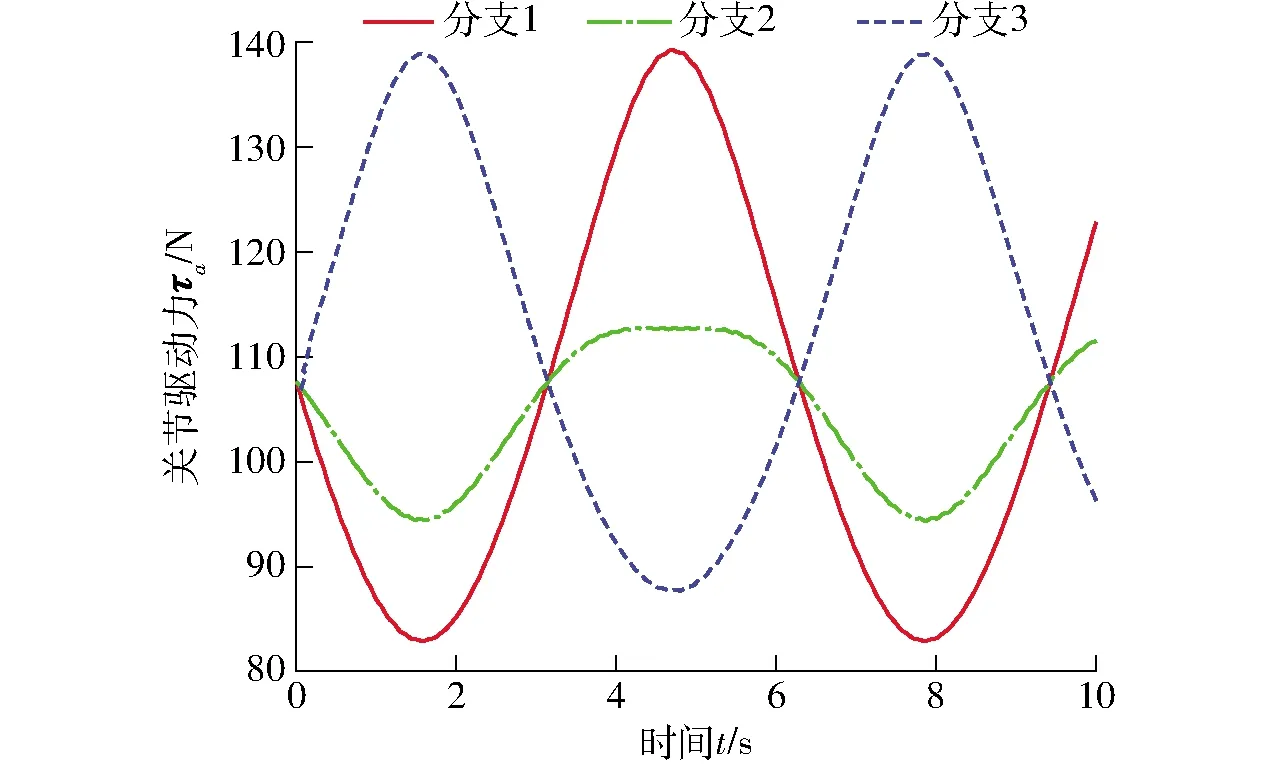
图5 关节驱动力软件仿真值Fig.5 Software simulation value of joint driving force

图6 关节驱动力偏差曲线Fig.6 Deviation curves of joint driving force
4 调姿隔振平台模态分析
4.1 固有频率和振型
调姿隔振平台的动力学方程是一个强耦合的非线性微分方程,其求解十分困难,因此在进行模态分析时,通常需要对其进行简化处理。方程中的重力项及弹簧预紧力是常数项,对系统的固有频率没有影响,可以忽略。同时,动力学模型中的科氏力项对固有频率的影响较小,计算时同样可以忽略[25]。上、下连杆的弹性刚度、电动缸的伺服刚度都远远大于弹簧刚度,可以视为无穷大。
(44)
其中
Ku=diag(k1,k2,k3)
式中Ku——刚度矩阵
无阻尼系统振动固有频率与刚度矩阵和质量矩阵存在关系[26]
|Ku-λMuu|=0
(45)
其中
式中λ——特征值
ωn——系统固有圆频率
求解特征方程(45)可以得到系统的特征值λi和固有圆频率ωni(i=1,2,3),进而可求得各特征值对应的主振型u(i)。

(46)
根据式(46),正则主振型可以表示为
进一步,可得到正则振型矩阵为

(47)
给定弹簧刚度k1=k2=k3=14.00 N/mm,得到机构在初始位姿下的固有频率和正则振型如表3所示。操作空间的正则振型为6×1的列向量,前3个量表示转动,后3个量表示移动。从表3可以看出,一阶振型中前5个元素为零,表示机构只有沿z轴移动的自由度。从二阶振型可以看出,机构只具有绕水平面上某一轴线转动的自由度,其x、y轴的移动分量是转动耦合产生的。机构的二、三阶固有频率相同,但其对应的正则振型并不相同。从表3中可以看出,二、三阶振型是正交的,其转动轴线在水平面上相互垂直,轴线分布如图7所示。

表3 机构初始位姿固有频率及正则振型Tab.3 Natural frequency and normal modes at initial pose of mechanism

图7 二、三阶振型轴线分布Fig.7 Distribution of axis of the second-order and third-order vibration modes
使用ADAMS Vibration的自由振动分析计算系统固有频率。模型中所有零部件均为刚体,振动为无阻尼振动。分析得到的各阶模态对应的无阻尼固有频率结果见表4。由表4可知,当动力学模型忽略滑块质量时,机构固有频率理论计算值与软件仿真值的误差超过30%。当动力学模型包含滑块、上下连杆及电动缸时,机构固有频率理论计算值和软件仿真值的误差在1%以内,说明所建立的完整动力学模型足够精确,可以作为进一步计算的理论依据。
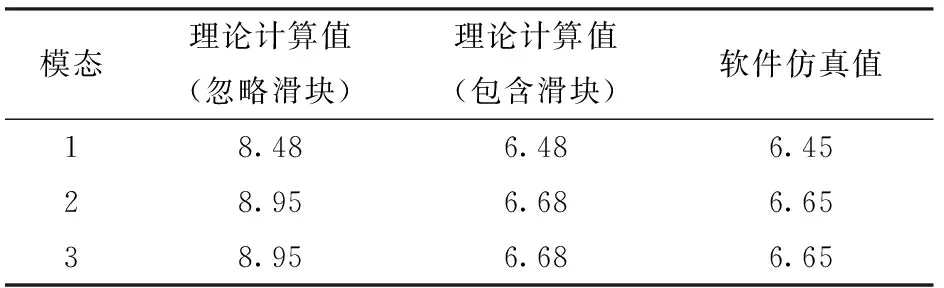
表4 机构固有频率对比Tab.4 Comparison of natural frequency Hz
4.2 固有频率影响因素分析
为了保证调姿隔振平台的对称性,3个弹簧刚度始终取相同的刚度。图8为系统一阶固有频率与弹簧刚度、动平台质量的关系曲面。从图中可以看出,随着弹簧刚度变大,系统固有频率相应变大,且变化幅度较大,说明了弹簧刚度是系统固有频率的关键影响因素。假定弹簧刚度不变,系统一阶固有频率随着动平台质量的增加而逐渐减小,但变化的幅度较小。二、三阶固有频率的变化规律类似,只是转动振型主要受到转动惯量的影响,而不是质量。
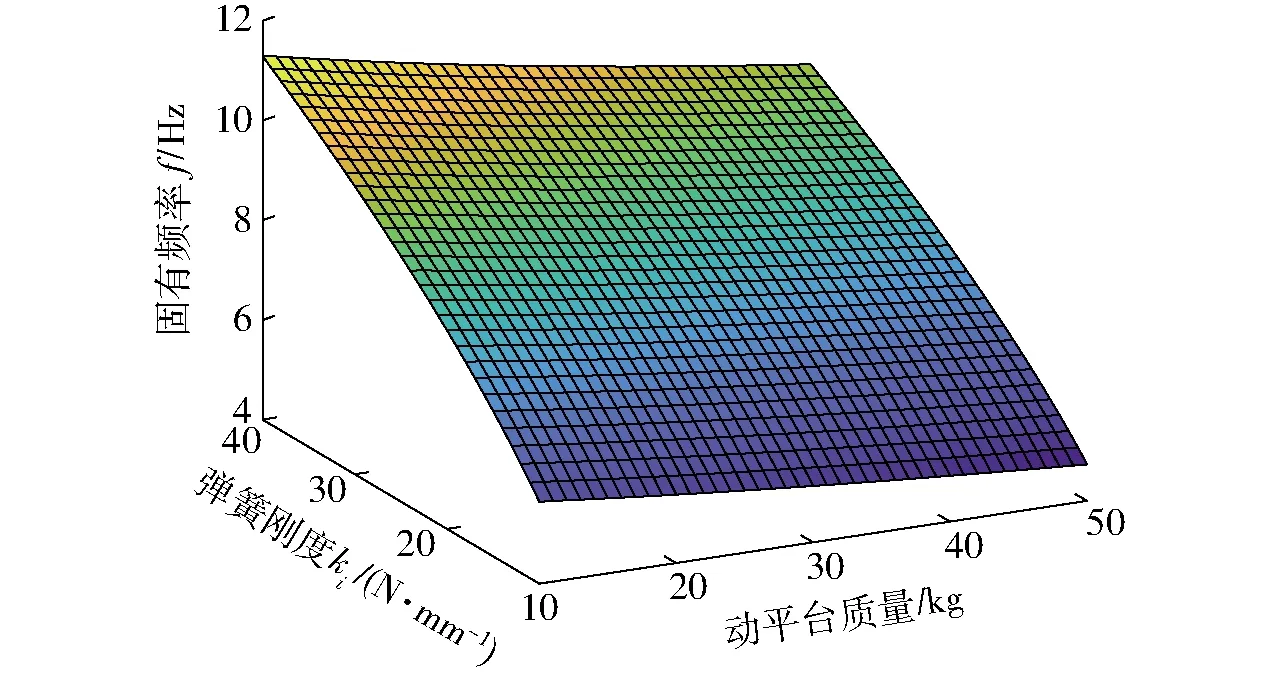
图8 一阶固有频率与弹簧刚度、动平台质量关系曲面Fig.8 Relationship among the first-order natural frequency, spring stiffness and mass of mobile platform
给定弹簧刚度k1=k2=k3=14.00 N/mm,机构各阶固有频率与机构位姿的关系如图9所示,每个图中3个曲面分别对应机构工作高度为h0-0.08 m、h、h0+0.08 m。
从图9可以看出,随着机构工作高度的增加,机构各阶固有频率均相应增加。以一阶固有频率为例,工作高度为h0-0.08 m、h、h0+0.08 m时,对应的最大固有频率分别为6.19、6.48、6.85 Hz,变化幅度较小。结合转动自由度,从图9中可以看出,在机构的各个极限位姿,固有频率的变化最大不超过2 Hz,对被动隔振的频率范围影响很小。
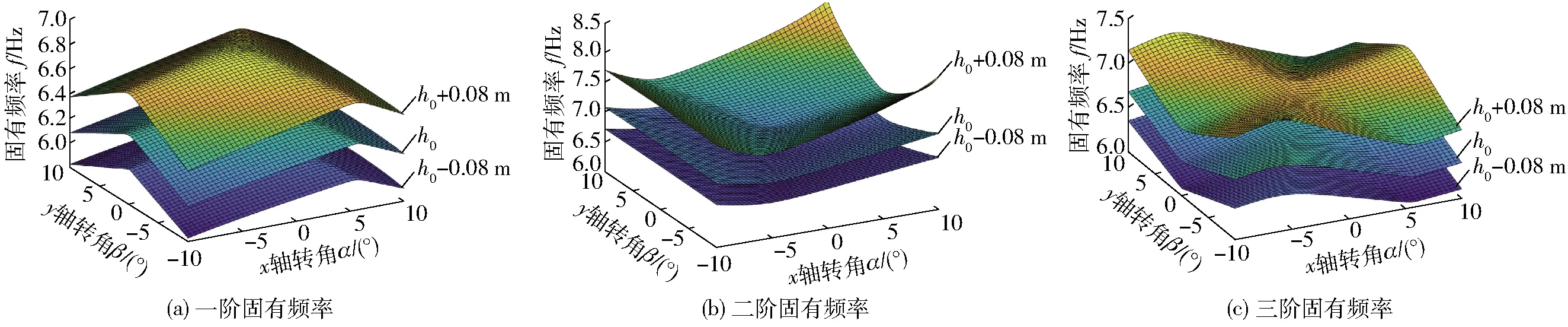
图9 固有频率与机构位姿的关系曲面Fig.9 Relationship between natural frequency and pose of mechanism
5 实验
5.1 实验系统
调姿隔振平台实验系统如图10所示,主要包括计算机、控制柜、调姿隔振平台原理样机、航姿传感器、振动传感器、振动信号采集器等。原理样机主要包括动平台、定平台、上连杆、下连杆、电动缸、被动隔振单元等。

图10 调姿隔振平台实验系统Fig.10 Experimental system of orientation adjustment and vibration isolation platform1.计算机 2.振动信号采集器 3.控制柜 4.航姿传感器 5.动平台 6.振动传感器 7.上连杆 8.下连杆 9.被动隔振单元 10.电动缸 11.定平台
被动隔振单元结构如图11所示。下连杆通过支座连接在直线导轨的滑块上。直线导轨夹具通过螺栓固定在转接板上,可以将直线导轨滑块固定在任意位置,方便后续工作模式的切换。弹簧导向轴通过自润滑轴承与支座连接,形成移动副,增加直线轨道的抗倾覆约束力。立板上均布有3个螺纹孔,通过螺栓的松紧来调整垫片与立板之间的距离,进而调整弹簧预紧力及滑块初始位置。拉线编码器实时测量滑块位移。

图11 被动隔振单元结构图Fig.11 Structure diagram of passive vibration isolation unit1.弹簧 2.导向轴 3.下连杆 4.自润滑轴承 5.拉线编码器 6.导轨 7.滑块 8.支座 9.转接板 10.导轨夹具 11.垫片 12.立板 13.调整螺栓
从式(44)中可以看出,弹簧刚度是调姿隔振平台振动方程的重要参数。实验用弹簧为圆柱螺旋压缩弹簧,端部线圈折弯靠紧,端面磨平。弹簧刚度理论计算公式为
(48)
式中G——剪切弹性模量
φ——弹簧钢丝直径
n——弹簧有效圈数
D——弹簧中径
实验用弹簧参数为:线径4 mm,中径28 mm,总圈数11圈,有效圈数9圈,材质65Mn,采用式(48)计算得弹簧刚度为12.96 N/mm。式(48)是根据材料力学推导出来的,很难精确计算弹簧刚度,因此采用弹簧拉压试验机对其进行刚度测量,刚度实际测量值为14.00 N/mm。将虚拟样机弹簧刚度设定为同等参数,使虚拟样机与原理样机的关键物理参数接近。
5.2 模态实验
如图12所示,将3个滑块预紧,并用自锁式尼龙扎带将3个滑块扎紧,采用突然剪断扎带的方法将脉冲信号施加给机构,实现对机构的脉冲激励,从而激发出机构的各阶模态。

图12 原理样机的脉冲激励方式Fig.12 Pulse excitation of prototype
如图10所示,在拾振点1、2处布置IEPE加速度传感器、在拾振点3处布置IEPE速度传感器。突然剪断扎带后,机构受到脉冲激励,动平台响应的时域图信号如图13所示。对时域信号进行离散傅里叶变换,得到系统的输出响应的频谱图,如图14所示。在图13、14中,vpi、api分别表示第i个拾振点的线速度、线加速度。

图13 动平台输出响应时域波形Fig.13 Time domain waveform of output response of mobile platform

图14 动平台输出响应频域波形Fig.14 Frequency domain waveform of output response of mobile platform
相比于电动缸、动平台、上下连杆等零部件,弹簧的刚度要小很多,因此测试得到的低阶固有频率就是系统的刚体模态。由于3个滑块是同步突然释放,上述脉冲激励起的模态以一阶模态为主。从图14可以看出,3个拾振点的频域波形基本一致,原理样机的一阶振型固有频率约为7.50 Hz。实验测定值7.50 Hz与理论计算值6.48 Hz接近,但仍存在一定偏差,主要是激励过程中机构的位姿变化、弹簧多次大行程压缩后的刚度变化、3个滑块释放的不一致性、理论模型的偏差等因素造成的。
5.3 响应特性实验
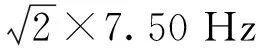
主动调姿运动的响应特性直接决定了调姿隔振平台低频段位姿扰动的补偿能力。本实验主要验证原理样机在7 Hz的响应特性。分别给定原理样机绕y轴运动的正弦信号为β=1.5°sin(2π×2t)、β=1.5°sin(2π×7t),即正弦信号幅值为1.5°,频率分别为2、7 Hz。Mti-300型航姿传感器实际测量的y轴输出曲线如图15所示。

图15 不同工作频率下原理样机的y轴输出曲线Fig.15 The y-axis output of prototype at different operating frequencies
从图15可看出,由于安装偏差及零漂,传感器的输出零线存在偏差。原理样机的运动频率为2 Hz时,频率较低,y轴实测输出幅值100%复现了命令振幅。原理样机的运动频率为7 Hz时,y轴实测输出幅值至少80%复现了命令振幅,超过了伺服系统频率响应带宽定义中的70.7%。
给定样机绕x轴相同的7 Hz正弦信号,图16为Mti-300型航姿传感器实际测量的样机x轴输出曲线。同样,原理样机频率7 Hz的x轴输出幅值至少相当于命令振幅的80%,较好地复现了命令信号。上述实验结果说明,对于7 Hz以下的输入指令,原理样机具有较强的跟随能力,能够实现对低频位姿扰动的补偿。

图16 频率7 Hz下原理样机的x轴输出曲线Fig.16 The x-axis output of prototype at 7 Hz
6 结论
(1)针对大幅度位姿扰动补偿和中高频振动隔离的需求,提出了一种主被动闭环融合的并联调姿隔振平台新构型。
(2)借助于旋量代数及影响系数理论,建立了包含闭环子链并联机构的运动学模型,得到了动平台、开链分支、电动缸分支对广义坐标的一、二阶影响系数。
(3)基于旋量形式牛顿-欧拉公式及虚功原理,建立了包含闭环子链并联机构主被动分离形式的动力学模型,并以此为基础求解了调姿隔振平台的固有频率及振型,分析了弹簧刚度、平台质量、机构位姿对系统固有频率的影响。
(4)模态实验得到的原理样机固有频率与理论计算值接近,验证了理论模型的正确性,响应特性的实验结果验证了原理样机大幅度位姿补偿的可行性。
