MHD对流三维Boussinesq方程组解的存在性
2022-08-05朱芷逸李俐玫张诗语
朱芷逸,李俐玫*,张诗语
(四川师范大学 数学科学学院,四川 成都 610068)
0 引言
研究磁流体(MHD)耦合Boussinesq方程组[1]
(1)
满足初始条件
u(x,0)=u0,θ(x,0)=θ0,H(x,0)=H0(2)及Slip边界条件
温度θ满足Neumann边界条件
∂nθ=0,x∈∂Ω,
(5)
这里Ω⊂R3是光滑有界区域,u是速度场,H是磁场,θ是温度,μ是流体粘性系数,κ是热扩散系数,γ是磁扩散系数,n是曲面∂Ω的单位外法向量.
如果流体不受洛伦兹力影响,即H=0,那么方程组(1)就成为无扩散的经典Boussinesq方程.近年来有大量学者研究Boussinesq方程,Bona[2]研究了广义Boussinesq方程组光滑解的存在性和孤立波的稳定性,Bian等[3]研究了具有分层效应的MHD对流二维Boussinesq方程,Guo[4]研究了一类Boussinesq方程在Navier-Slip边界条件下的适定性问题,证明了在H1范数意义下强解的局部存在唯一性.Luo等[5]证明了在环面上二维Boussinesq方程有限能量弱解的存在性,Stokes等[6]考虑了流体中的耦合力对磁流体通道的影响.从方程结构来看,Boussinesq方程与Euler方程、Stokes方程、MHD方程有着重要联系,Beale等[7]证明了三维Euler方程光滑解的爆破性,Chae等[8]考虑在外力f(x,t)作用下,不可压缩非均匀无粘二维流与θ(x,t)相互作用的运动.对于边界条件,最经典的就是no-slip边界条件
u=0,x∈∂Ω.
假设流体颗粒由于正粘度而黏附在边界上,这个边界条件最先由Stokes[9]提出,它的含义是流体颗粒由于正粘度而黏附在边界上.虽然在no-slip边界条件下,可以得到Navier-Stokes方程组解的适定性,但是难点在于求解过程中边界的处理[10-12].另一个比较常用的就是Navier-Slip边界条件[13]
u·n=0, [2(S(u)n)+γu]τ=0,x∈∂Ω,
其中2S(u)=u+(u)T是粘性应力张量,γ是光滑函数.广义Navier-Slip边界条件[14]为
u·n=0, [2S(u)n+Au]τ=0,x∈∂Ω,
其中A是光滑对称张量.Vorticity-Slip边界条件[15]为
u·n=0,n×ω=βu,x∈∂Ω,
其中β是光滑函数,ω=×u是流体的涡量.
文中研究不可压缩MHD方程耦合Boussinesq方程在Slip边界条件下,温度θ在Neumann条件下,系统(1)~(5)弱解的整体存在性和强解的局部存在唯一性.
1 预备知识
文中Ω⊂R3是光滑有界区域,内积记为(·,·),标准的Sobolve空间Hs(Ω)(s>0),范数||·||m=||·||Hm和||·||L2=||·||,V*是V的对偶空间,我们将Ω省略.记函数空间
对任意u∈V,有
引理1[16]令Stokes算子A=-Δ的定义域满足D(A)=W⊂V是正闭双线性型的自伴扩张算子,则有
它的逆是紧的且有可数多个特征值λj,使得0<λ1≤λ2≤…→∞,相应的特征向量ej⊂W∩C∞构成X的一组完备正交基.
为了方便表示,将方程组(1)的非线性项记为
2 弱解的整体存在性
下面通过Galerkin逼近法,建立方程组(1)~(5)弱解的整体存在性.
定义1设Ω是R3中的光滑有界区域,(u0,H0)∈X,θ0∈L2.若(u,H)∈L∞(0,T;X)∩L2(0,T;V),(u′,H′)∈L1(0,T;V*),θ∈L∞(0,T;L2)∩L2(0,T;H1),θ′∈L1(0,T;(H1)*),且
那么函数(u,θ,H)是方程组(1)~(5)的弱解,测试函数Ψ∈V,φ∈H1.
定理1设Ω是R3中的有界光滑区域,(u0,H0)∈X,θ0∈L2,则对任意给定的时间T>0,方程组(1)~(5)在[0,T)上至少存在一个弱解,且在分布意义下满足如下能量估计:
其中ε1>C/4μ.
证明分别定义逼近解u(m)(t),θ(m)(t),H(m)(t)为
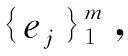
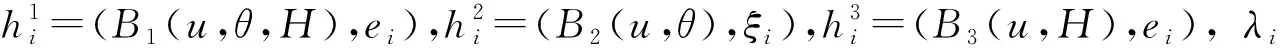
(7)
将(7)式的三个方程分别与u(m),θ(m),H(m)做内积可得
再将(8)~(10)式相加得到
结合Hölder不等式、Young不等式及(11)式可得
将(12)式两边同时在[0,T]上积分就可以得到能量不等式(6).进一步可得
取Ψ∈V,φ∈H1,则
将方程组(7)的第一式和第三式分别与Ψ做内积,第二式和φ做内积可得
(13)式中的非线性项有如下估计:
同理可得
由此可以得到非线性项的有界性:
于是
由以上过程可得方程组(1)~(5)全局弱解的存在性.】
3 强解的局部存在唯一性
定理2令(u0,H0)∈V,θ0∈H1,则对给定的T*>0,T*仅依赖于u0,H0,θ0,方程组(1)~(5)存在唯一的强解(u,H,θ)在[0,T*)上满足(u,H)∈L∞(0,T;V)∩L2(0,T;W),(u′,H′)∈L2(0,T;X),θ∈L∞(0,T;H1)∩L2(0,T:H2),θ′∈L2(0,T;L2),并且对任意的T∈(0,T*),有
证明分别用×,,×作用于方程组(7)的第一式、第二式和第三式,再分别和×u(m),θ(m),×H(m)做内积相加得到
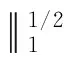
同理可得
将(21)~(26)式带入(20)式即可得到能量不等式
其中C1=μ-ε1-ε2-ε4-ε8,C2=κ-ε5,C3=γ-ε3-ε6-ε7.由能量不等式(27)可得
方程组(7)的第一式、第二式和第三式分别与∂tu(m),∂tθ(m),∂tH(m)做内积上可得
由(28)式可得
同理,由(29)式和(30)式可得
将(31)~(33)式相加可得
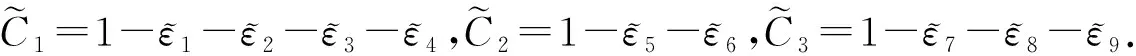

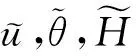
其中
同理可得
将(37)~(42)式相加得到
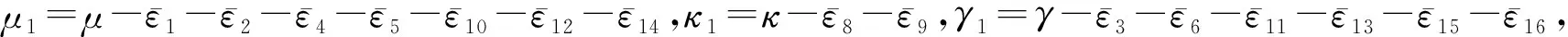
由Gronwall不等式和初值
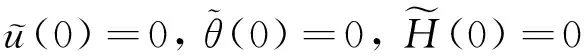
得到u=u1,θ=θ1,H=H1.】
