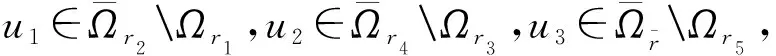含平均曲率算子的拟线性微分方程Dirichlet问题三个正解的存在性
2022-08-05何志乾
何志乾
(青海大学 基础部,青海 西宁 810016)
近年来,许多学者研究了含平均曲率算子的拟线性微分方程Dirichlet问题[1-3]
(1)
正解的存在性和多解性,并取得了许多深刻的结果.问题(1)有非常重要的应用背景,它可以刻画不可压缩流体的毛细现象以及人类角膜的几何形状等[4-5].
问题(1)是一类拟线性非一致椭圆问题,研究这类问题有许多实质性的困难,即便以最简单的一维情形为例,问题(1)解的梯度也会出现爆破,这就导致一些经典的方法不能直接应用.鉴于此,一些学者研究了含平均曲率算子的一维Dirichlet问题
(2)
正解的存在性和多解性[6-10],其中λ为正参数,f∈C([0,∞),[0,∞))并且f(u)>0,u>0,主要工具包括变分法、上下解方法、时间映像法等.但很少有学者利用锥上的不动点定理研究问题(1)正解的存在性和多解性.2014年,Lu等[11]巧妙地构造了一个锥,以便利用不动点指数理论获得问题(2)至少一个或两个正解的存在性.据我们所知,很少有学者研究问题(2)至少三个正解的存在性.
受以上文献的启发,文中利用锥上的不动点定理得到问题(2)至少三个正解的存在性,部分改进文献[11]的主要结果.
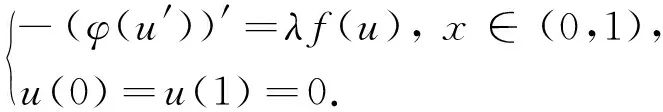
(3)

文中主要结果如下:
定理1设f∈C([0,∞),[0,∞))且f(u)>0,u>0.若f0=f∞=0,则存在λ*,λ*>0,使得当λ*<λ<λ*时,问题(3)至少存在三个正解.
1 预备知识
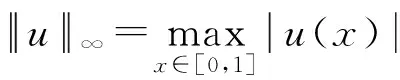
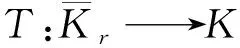
( i )若对∀x∈∂Kr有||Tx||≥||x||,则i(T,Kr,K)=0.
( ii )若对∀x∈∂Kr有||Tx||≤||x||,则i(T,Kr,K)=1.

( i )φ在[0,∞)上是上凸的,φ-1在[0,1)上凸;
( ii )对任意的0 证明由φ与φ-1的定义不难验证.】 引理3[11]令h∈C([0,1],[0,∞))且h≠0.假设w是问题 (4) 对任意的r>0,令 引理4[13]对任意的h∈C[0,1],问题(4)存在唯一解 由引理4可知,问题(3)的解等价于空间E中的算子方程 对任意固定的u∈P,有 引理5给定r>0,若ε>0足够小且Bλε<1,其中Bλε如引理2(ii)所示.若f*(r)≤εφ(r),则有||Tλu||∞≤Bλε||u||∞,u∈∂Ωr. 证明由Tλ的定义,对任意的u∈∂Ωr,有 引理6给定r>0,若u∈∂Ωr,则 ||Tλu||∞≤φ-1(λMr), 证明对任意的u∈∂Ωr,有f(u(x))≤Mr,从而 引理7[11]给定r>0,则对任意的u∈∂Ωr有||Tλu||∞≥σx*φ-1(λ(1-σ)x*mr),这里 定理1的证明因为φ是个有界算子,给方程(3)的两端同乘u′并且从0到x0积分,则当u′(0)→∞时,有 则由引理7可知,存在 使得对λ*<λ<λ*,有 ||Tλu||∞≥||u||∞,u∈∂Ωri,i=2,3,5. 由引理1可知i(Tλ,Ωri,P)=0,i=2,3,5. 对于给定常数r4>0,由引理6可知,当0<λ≤λ*时,||Tλu||∞<||u||∞,u∈∂Ωr4.由引理1可知i(Tλ,Ωr4,P)=1,所以 ||Tλu||∞<||u||∞,u∈∂Ωr1. 由引理1可得i(Tλ,Ωr1,P)=1.所以 最后,若f∞=0,λ<λ*,则由引理7可知
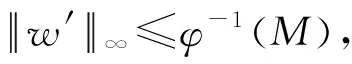



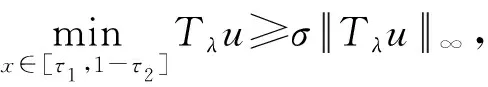
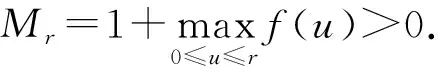
2 主要结果的证明