带有非线性阻尼的Kirchhoff型Berger方程的全局吸引子

徐 玲，张娟娟

(西北师范大学 数学与统计学院，甘肃 兰州 730070)

0 引言

考虑带有非线性阻尼的Kirchhoff型Berger方程

全局吸引子的存在性,其中Ω⊂Rn是一个具有足够光滑边界的有界区域,函数u(x,t)代表板的挠度,β是一个常数,它与作用在板上的压力成正比,h∈L2(Ω)描述板的横向负载,函数a(x)表示环境阻力,μ和α是大于0的常数.

设函数σ(s),g(s)和a(x)满足如下条件:

(W1)函数a∈L∞(Ω),并且存在正常数α0,使得

a(x)≥α0>0,x∈Ω.

(4)

(W2)函数σ∈C1(R)严格增,σ(0)=0,且

其中当n≤4时，1≤q<∞；当n>4时,1≤q≤(n+4)/(n-4).

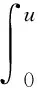
其中当n≤4时，1≤p<∞；当n>4时,1≤p≤4/(n-4)，λ1是Δ2的第一个特征值.

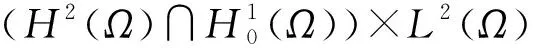
文中C和Ci(i=0,1,2,…)都表示正常数,在不同之处可表示不同的值.

1 预备知识

则A是空间H中的自伴算子，且在空间V2中是严格正的.可以定义算子A的能量为As(s∈R)，于是空间Vs=D(As/4)是Hilbert空间，并且具有如下的内积和范数：

显然，

||Δu||2≥Cλ||u||2.

(9)

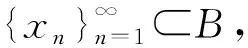
则称X×X上的函数φ(·,·)是定义在B×B上的收缩函数.

记C(B)为定义在B×B上收缩函数的集合.

定理A[8]设{S(t)}t≥0是Banach空间(X,||·||)上的一个半群,B0是该半群上的一个有界吸收集.进一步,假设对任意的ε>0,存在T=T(B0,ε)和φT(·,·)∈C(B0)，使得

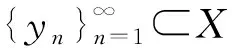
引理1[9]设非线性函数σ(s)满足条件(W2),则对任意的δ>0,存在常数Cδ>0,使得

类似于文献[6]定理2.1，可以得到问题(1)～(3)解的存在性和唯一性.

定理1假设条件(W1)～(W3)成立，初值(u0,u1)∈V2×H，则对任意的T>0,问题(1)～(3)有唯一解(u,ut)∈C([0,T];V2×H),并且(u,ut)连续依赖于初值(u0,u1).

根据文献[4,10,11]可知，在(4)～(8)式成立情况下，问题(1)～(3)的解算子S(t)(u0,u1)=(u(t),ut(t))(t≥0)在能量空间V2×H中产生了一个半群,记作{S(t)}t≥0.

2 有界吸收集的存在性

引理2假设(W1)～(W3)成立，则问题(1)～(3)对应的半群{S(t)}t≥0在空间V2×H中存在有界吸收集.

证明用方程(1)与ut在空间H中作内积可得

其中

结合(4)和(5)式可知

E(t)≤E(0), ∀t≥0.

(14)

进一步,由(4)和(5)式可得,存在δ1>0和Cδ1>0，使得

由(8)式可知,存在λ1>λ′>0和C0,使得

运用Young不等式，由(18)式可得

根据(9)和(19)式可得

其中ε>0足够小,使得

联立(12)～(14)及(20)式可得,对任意t≥0,有

由(5)和(6)式可知

运用Hölder不等式和Young不等式,结合(4),(5)式和(22)式可得如下估计：

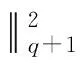
将v=ut+δ1u(δ1由(15)式定义)代入方程(1)可得

用v与(24)式在空间H中作内积,有

(25)

其中

根据(9)和(19)式，有

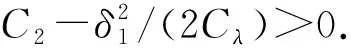
其中CE(0)是依赖于δ1,Cη,E(0)的常数；η>0足够小,使得1-(λ′+ε)/Cλ-η>0.所以

给(25)式从0到t进行积分,并结合(21),(28)～(30)式可以推出

其中C8=C7/C4.因此,对ρ>C6/C5,存在t0,使得||ut(t0)||2+||Δu(t0)||2+||u(t0)||4≤ρ.

定义

显然,B1是空间V2×H中的有界吸收集.】

3 全局吸引子的存在性

本节首先运用能量不等式进行先验估计,然后证明空间V2×H中半群{S(t)}t≥0的渐近紧性，最后证明问题(1)～(3)对应的半群{S(t)}t≥0全局吸引子的存在性.为了方便起见,用B1表示空间V2×H中半群{S(t)}t≥0的有界吸收集,并记

3.1 先验估计

初始条件为

用w(t)乘以(32)式，并对其在[0,T]×Ω上进行积分,可得

在[0,T]上对Ew(t)关于t积分,结合(33)式,有

用wt(t)乘以(32)式，并在[s,T]×Ω上积分可得

对(35)式在[0,T]上关于s积分,可得

进一步,取s=0,则由(35)式可知

进而结合(4)式和引理1可得

下面估计

首先用(ui)t(t)乘以方程(1),然后对其在Ω上积分,最后结合有界吸收集存在性的证明可以推出

(39)

其中

类似于(23)式的估计方法,运用Hölder不等式,结合(5),(22)和(39)式可得,当i=1,2时，有

联立(34),(36),(38),(40)式可以推出

(41)

其中

3.2 渐近紧性

定理2假设条件(W1)～(W3)成立,则问题(1)～(3)对应的半群{S(t)}t≥0在空间V2×H中是渐近紧的.

证明因为半群{S(t)}t≥0有有界吸收集,所以对任意固定的ε>0,取δ≤ε/(2meas(Ω)),取T足够大,使得CT/T≤ε.根据定理A,只需证明对于固定的T,函数ΦT(·,·)属于C(B1).

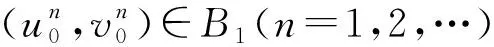
下面计算(43)式中每一项.根据(4),(44)和(47)式,有

由(49)式可知

由解的光滑性,则有

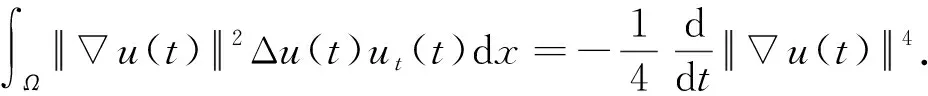
结合(44),(45)及(48)式，先让m→∞，再让n→∞,可以推出

类似地,可以得到

同时,对每个固定的T,因为

是有界的,所以根据Lebesgue控制收敛定理,有

由(46)式可知

结合文献[12]中的引理4.4,类似可以推出

综合以上各式,有ΦT(·,·)∈C(B1).】

3.3 全局吸引子的存在性

由引理2和定理2可以得到问题(1)～(3)全局吸引子的存在性.

定理3假设条件(W1)～(W3)成立，则问题(1)～(3)对应的半群{S(t)}t≥0在空间V2×H中存在全局吸引子，且该全局吸引子是紧不变集.