面向船体结构动冰载荷监测的线性形函数识别方法研究

孔 帅， 田于逵， 崔洪宇， 季顺迎

(1. 中国船舶科学研究中心 水动力学科研部，江苏 无锡 214082; 2. 大连理工大学 工业装备结构分析国家重点实验室，辽宁 大连 116024)

极地丰富自然资源、便利水运交通和深刻地缘影响是刺激海洋强国研发建造冰区船的内在动力[1]，俄美加日韩及北欧诸国在冰区船研发领域均具有极强的话语权，其中俄罗斯拥有世界上数量最多、吨位最大且推进性能最好的破冰船队伍，目前仍在建造多艘重型破冰船以巩固其北极地位。《中国的北极政策》[2]指出“技术装备是认知、利用和保护北极的基础”，然而我国破冰船在总体船型、推进系统、冰带构件优化等方面均存在较大的技术短板[3]。冰载荷作为冰区船设计及安全评估中的关键输入始终是兼具科学及工程意义的研究热点，其可直接用于船型优化[4]、结构安全评估[5]和疲劳分析[6]等。

实船监测是认知掌握冰载荷的重要技术手段，可有效揭示冰载荷的数值范围[7]、分布特征[8]及统计特性[9]，其载荷识别算法作为监测系统核心近年来被广泛关注[10-11]。冰载荷识别中常用的影响系数矩阵法通过向待监测子区域依次施加单位载荷以形成关联起冰载荷矢量和冰激应变响应矢量的传递矩阵[12]，具有形式简洁、工程应用性强的优点，然而该方法尚未考虑冰载荷动载荷效应且不能解决加载位置偏离预期加载位置而导致求解异常的问题。另外，基于时域反卷积算法的动冰载荷识别模型中递推连锁计算格式会导致其求解矩阵维数过大和求解系数过多，影响求解稳定性和快速性[13]，进而导致结构安全状态误判和报警时机贻误。

动载荷识别的形函数法的核心思想为有限元分析理论中场变量的离散化处理，利用一组形函数和权重系数拟合动态荷载，把动态载荷时程的求解转换为个数有限权重系数的求解，缩减求解矩阵维数并提升载荷识别性能。该方法可有效识别移动载荷[14]、均布载荷[15]及集中载荷，分析识别算例可知其具有载荷识别类型范围广和适用性良好的优点。

为对冰区船冰载荷监测系统提供有效的载荷识别方法，本文将首先基于形函数方法建立冰载荷识别的正问题，其次讨论对反分析求解中遇到的不适定性问题并采用正则化方法控制求解，最后分别从数值算例和试验验证角度对提出的冰载荷识别模型进行验证性分析。

1 冰载荷识别的形函数理论

在连续时域内，船体结构由冰载荷引起的冰激响应可采用杜哈梅尔积分的形式表示[16-17]，即

(1)

式中:g(t)为对应响应与冲击载荷关系的Green核函数；p(τ)为冰载荷；ε(t)为冰激应变。

时域反卷积识别模型在反演冰载荷过程中，其识别系统对应反问题的适定性主要由式(1)中的小奇异值和测试信号噪声水平两个因素决定。实船冰载荷测量中冰激响应信号始终存在噪声信号的干扰，其可采用低通滤波以滤掉高频噪声或传感器合理布置以提升信噪比的方式控制。因此，决定冰载荷求解算法鲁棒性的关键在于控制反求矩阵的奇异性，而式(1)表示的反卷积型式因采样时间间隔均较小而导致其规模较大，进而导致矩阵不可避免的较大奇异性。

形函数方法可将荷载时间历程的识别转变为识别数目有限的形函数权重的求解，进而极大地降低系数矩阵的维数，提升计算效率和识别算法的鲁棒性。如图1所示将冰载荷p(t)在时间域内离散成m个等时间间隔的时间元Δt，在每个时间元内再选n个时间节点。

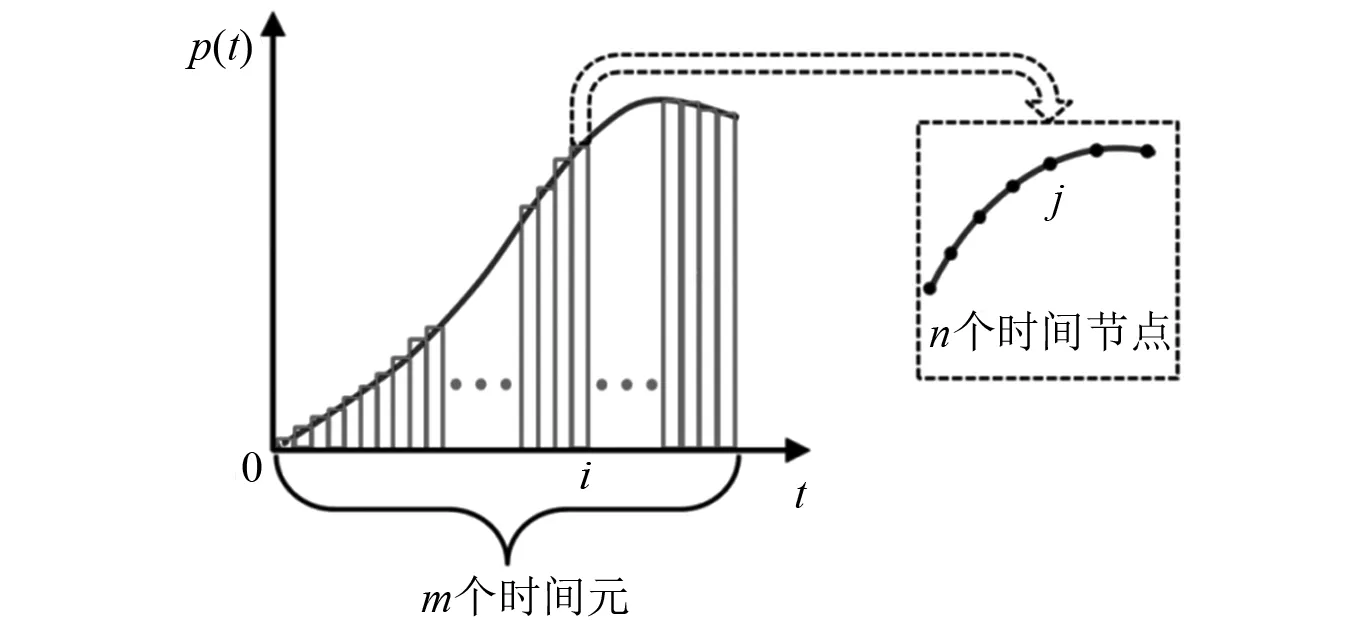
图1 基于线性分布形函数的冰载荷识别正问题Fig.1 Forward problem of ice load identification based on linear distribution shape function method

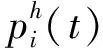
(2)

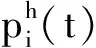
αi=[αi1αi2…αin]T

(3)

φi=[φi1(t)φi2(t) …φin(t)]T

(4)

Aiai=pi

(5)

(6)

求解Aiai=pi后可得权重系数矩阵ai，则

(7)

式中，Ni(t)为形函数，即

(8)

若将第i个时间元分为两个时间节点(即n=2)，则满足

[Ni1(t)Ni2(t)]

(9)

此时，Ni1(t)和Ni2(t)可采用线性分布形函数，其定义为

(10)

(11)

由有限元形函数理论可知式(10)和式(11)满足式(12)和式(13)所示的两条性质，其中式(12)表示在任意时间元内其形函数之和始终等于1，式(13)表示形函数在自身节点j处时的取值为1，而在其他时间节点时(即k≠j时)为零。这两条性质可有助于检验形函数构造的合理性和保障节点载荷与单元内近似冰载荷之间的连续性。

(12)

(13)

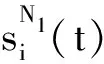
(14)

则可将式(14)写成矩阵形式

ε=Sp

(15)

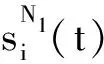
船体外板结构监测区域的冰压识别问题对应多源载荷识别问题，其需要将整个监测区域划分为众多子区域。船体结构在多源载荷作用下的响应是各个监测子区域上载荷引起响应的线性叠加，因此可将多源载荷识别问题可写成

(16)

式中:M为需要监测子区域的数目；N为测点的数目；pi为每个监测子区域上的冰载荷时程；εi为测点上的应变时程；Sij为i监测子区域上冰载荷与j测点应变之间的形函数矩阵。

由此，建立了基于线性分布形函数理论的冰载荷识别模型的正问题。

2 共轭梯度最小二乘正则化算法

已知冰激应变响应ε和形函数矩阵S对冰压p进行求解的反分析过程通常无法直接用最小二乘法或Moore-Penrose逆法，载荷识别时也通常要引入正则化方法[19-21]。适用于求解大维数、非对称和非正定方程的共轭梯度最小二乘算法(conjugate gradient least squares, CGLS)是一种高效算法[22]，可较好地识别壳结构和锯齿结构所受的环境载荷。相比于较为常用的截断奇异值分解(truncated singular value decomposition, TSVD)等直接型正则化算法，CGLS算法是一种迭代型算法，其每次迭代过程中的搜索方向是两两共轭的，且其搜索方向是负梯度方向与上一步搜索方向的组合，而截断奇异值分解方法则需利用正则化参数优选方法对其小奇异值进行截断以保证求解的适定性。因而，CGLS方法与TSVD方法的相似之处在于两者均是在已知边界约束情况下，根据与原不适定求解问题构造相“邻近”的适定问题以得到原问题的近似解，而区别在于求解步数、正则化算子及其能力提升方法等方面。

CGLS算法首先要对矩阵S进行正规化处理和相关计算量的初始化

STSpk=STp

(17)

p1=0,r1=εerr,q1=STr1

(18)

式中：p1为共轭梯度算法的初始解;r1=εerr为解的残差的初始值;q1为共轭迭代过程中间量的初始值。

当k>1时，共轭梯度最小二乘迭代算法过程为

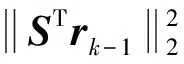
(19)

pk=pk-1+αkqk-1

(20)

rk=rk-1-αkSqk-1

(21)

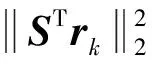
(22)

qk=STrk+βkqk-1

(23)

式中:αk，βk，qk为共轭迭代过程中间量;rk为迭代k次之后解的残差。

CGLS正则化算法属于半收敛算法，不合适的迭代步数会导致“过拟合”或“欠拟合”。CGLS正则化算法在进行冰载荷识别时滤波因子在不同求解时间步及迭代步数时均不同，故需要恰当的终止迭代准则以提升算法的正则化能力。本文采用Paige等[23-24]针对最小二乘问题提出的终止迭代法则(式(24))，该终止准则可较为有效判别当前迭代步数是否为最佳迭代终止点

(24)

式中:γ为正常数；rk为解的残差。

结合形函数理论与共轭梯度最小二乘正则化算法，其总结的冰压识别技术流程图如图2所示，分为冰载荷识别模型构建、结构冰激应变获取和冰压稳定识别算法三个部分，其逻辑及递进关系见图2。

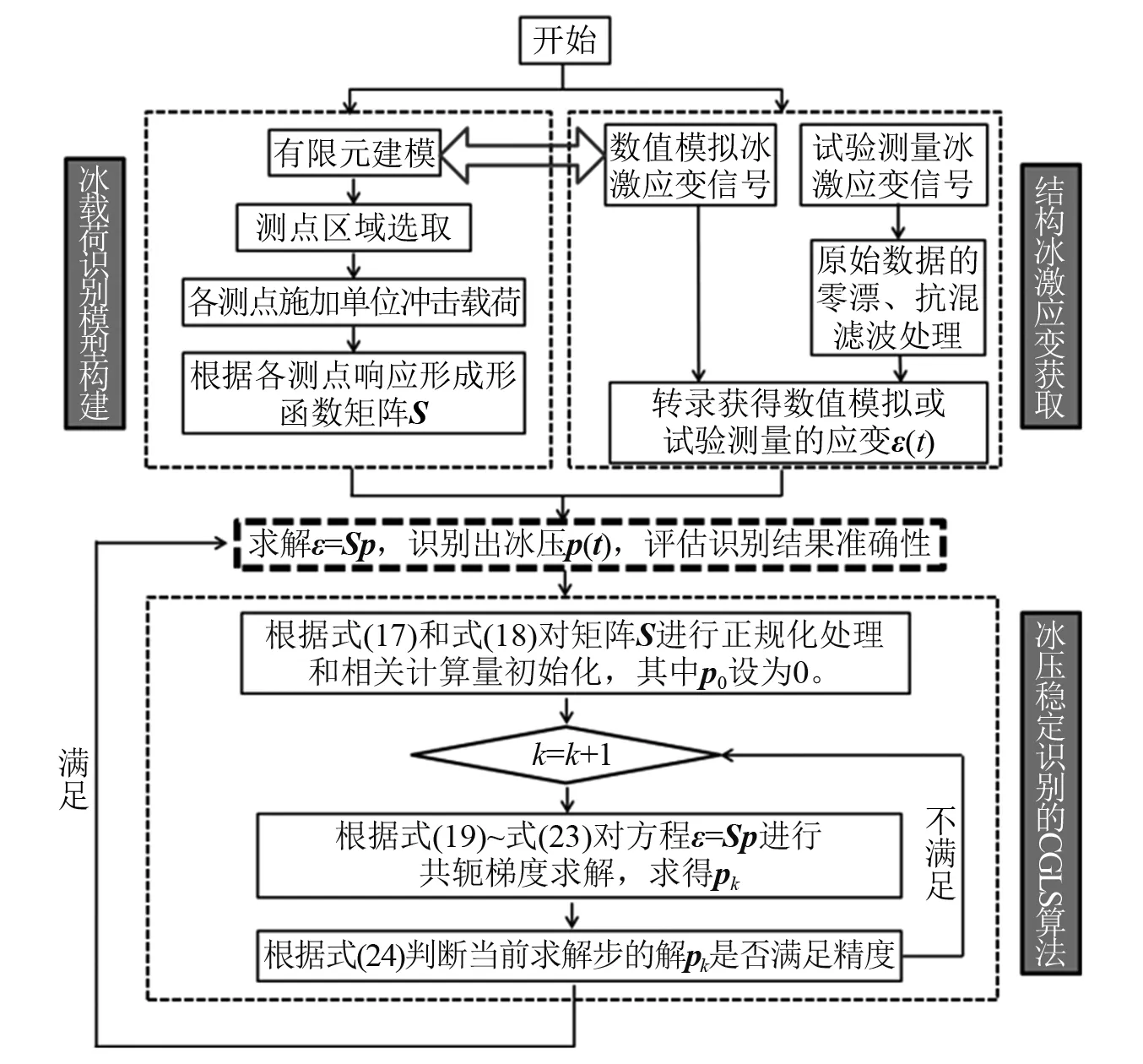
图2 基于形函数理论及CGLS算法冰压识别的流程图Fig.2 Flow chart of the ice pressure identification using the shape function theory and CGLS algorithm

3 冰载荷识别模型验证性分析

至此，基于形函数方法和共轭梯度最小二乘正则化算法的冰载荷识别模型建立，该算法的有效性可通过数值分析及试验验证进行检验。

3.1 数值分析

为从数值角度检验冰载荷识别算法，本文建立的结构模型主要参考中国极地科考破冰船“雪龙2号”外板结构和冰载荷承载力研究工作中的典型破冰船外板结构，该外板由肋骨、强肋骨、纵桁和外板组成，具体尺寸信息标记于图3中。在冰载荷识别过程中，船体结构假设处于线弹性阶段。结构阻尼选择为比例阻尼。弹性模量为206 GPa，泊松比为0.3，结构钢材密度为7 850 kg/m3。边界条件参考ABS冰级船规范标准，在模型的上下平面内边的边界设置为在x方向自由，左右平面内边的边界设置为关于yoz面对称。有限元模型中间部分采用网格尺寸为50 mm×50 mm较为精细的网格，为提升计算效率，其余部分采用了尺寸为150 mm×150 mm网格。冰载荷监测区域选择中间区域，对应监测面积为2.8 m×3 m；肋骨冰激应变监测是目前主流技术手段，故应变测量选择靠近肋骨边缘且测试方向平行于外板的应变。

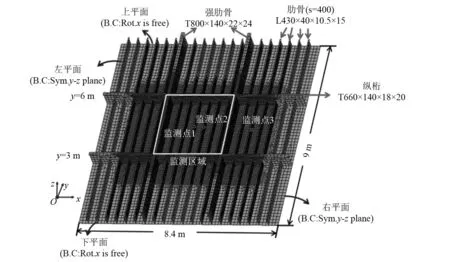
图3 典型冰区船舶外板结构有限元模型Fig.3 FE model of the typical shell structure of ice-going vessel

实船冰载荷测量中，其冰激响应信号始终存在噪声的干扰，噪声信号会对识别数值产生较大的干扰。为分析噪声信号对冰载荷识别模型干扰程度，本文采用加性噪声的形式进行添加，其实际结构测量的信号可写作[25-26]

εerr=ε+lnosiestd(ε)rand(-1,1)

(25)

式中:εerr为含有噪声信号的应变信号；lnosie为一个百分数，表示噪声水平；std(ε)为ε标准差；rand(-1,1)为(-1,1)之间的随机数。

图 4(a)与图4(c)为在监测点1基于形函数方法识别的冰载荷与施加载荷时程对比，选择两种波形的载荷时程，其采样时间元Δt选择为0.01 s。同时，为模拟冰载荷时程的随机特性，在两个载荷时程在建立时考虑了加载速率、波形特征及峰值差异等影响。分析外板结构冲击试验结果可知平行外板方向布放的传感器灵敏度最高，最能有效反应载荷信号特征，主要原因是船侧肋骨在甲板、纵桁约束下组成的梁结构在冲击载荷作用下发生“整体弯曲变形”效应，相比于“局部挤压”、“整体剪切变形”等效应更为突出。图4(b)为工况一(t=0.25 s时)监测区域的应变云图，其与真实模型试验的响应特征是相互对应的，即靠近肋骨边缘应变(平行外板方向)受“整体弯曲效应”影响较大，验证了模拟响应的可信性。可以看出无噪声干扰时载荷识别结果与施加载荷时程之间吻合性较好。参考实船冰载荷测试经验[28-29]，冰激应变的噪声水平普遍分布在1%～10%。为评估识别算法在极高噪声水平干扰下的适用性，图4也增加了20%高噪声水平干扰时的载荷识别结果。可以看出，当有20%噪声干扰时识别结果会因其识别模型的连锁计算格式受到影响，但仍能较为准确描绘出施加载荷的时程特征和峰值特征，识别相对误差为13.31%。冰载荷监测中的识别算法的求解速度决定了实时监测的报警效率，冰载荷识别模型由型号为Intel Core i7-9700的CPU处理器运行，运行时间为0.36 s；而采用时域反卷积算法的运行时间则为7.46 s，形函数法在求解速度上具有较强的优势，实时性更加突出。

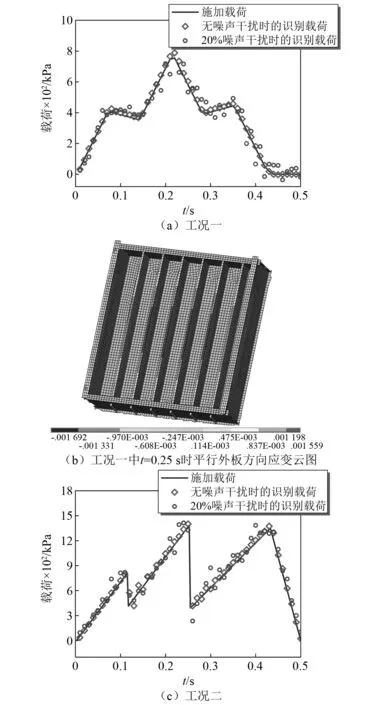
图4 形函数法的冰载荷识别结果Fig.4 Ice load identification results using the shape function method

为研究测点位置及测点数目对载荷识别结果的影响，在图3模型选择了三个监测点，表1列出了为研究影响因素所采用的监测对比方案说明。

表1 监测识别影响因素评估方案Tab.1 Evaluation scheme of influence factors in the identification

当测点位置选择距监测区域0.8 m的监测点3进行识别时，20%高噪声水平干扰下载荷识别相对误差为15.59%，这主要缘于测点位置的偏远会加重形函数矩阵奇异性，而运行时间与作用点几乎一致。当选择测点1和测点2时，其多源识别问题中的形函数矩阵规模是单源识别问题中形函数矩阵的N2(N=2为测点数量)倍，矩阵奇异性会增强；导致在20%高噪声水平干扰下多源载荷识别平均相对误差为16.41%，运行时间也延长至0.48 s。

3.2 试验验证

现场测量中很难布置大型加载装置以进行加载测试，故基于含有肋骨构件的外板结构载荷识别试验是检验模型准确性较为直接有效的方式。本文采用的外板结构由外板、肋骨、强肋骨和纵桁等组成，如图5所示。模型采用3 mm厚的6061铝合金板，试验模型的边界采用螺栓和边条组合方式进行约束。模型的弹性模量、材料密度和泊松比分别设为70 GPa,2 700 kg/m3和0.3。图5右侧为对应的测量位置，测量位置的应变片粘贴方式如图5中的右上角方框内的示意图所示。应变片的线路连接采用带温度补偿片的半桥连接方式。动载荷识别试验中应变信号和力信号同时由DH5922数据采集系统记录，采样频率10 kHz。为保证肋骨与真实结构之间的结构相似性最大化，肋骨纵向端部与纵桁相固定，且监测及测量的位置均远离边界。

图5 载荷识别试验装置Fig.5 Experimental facility in the load identification

图5左上角外板方形区域为对应的载荷测试区域，试验过程中采用力锤施加载荷，其灵敏度为3.10 mV/N。利用力锤连续向图5所示载荷测试方形区域施加四次力，图6中的实线部分即为对应的施加载荷时程，图6中虚线为识别的载荷时程。冰激应变信号预处理首先围绕冲击力作用时刻进行截取，然后采用去零漂及抗混滤波技术进行信号处理，转录接近真实的冰激应变信号，操作步骤如图2右上角所示。然后，按图2所示整体技术路线图将冰压进行识别，获得测试区域的施加力的识别值。可以看出，因结构自身阻尼和振动特性影响，识别载荷时程会稍迟滞于施加载荷时程并且在脉冲信号尾部出现波动现象。然而，识别载荷仍能较好地描述施加载荷时程特征。另外，实船测试中冰载荷时程具有随机特性且识别结果通常会受到周边结构上作用载荷的干扰，故各国学者常选取冰载荷峰值作为统计分析的参数，本算例中识别载荷峰值与施加载荷峰值之间相对误差均值仅为3.21%。

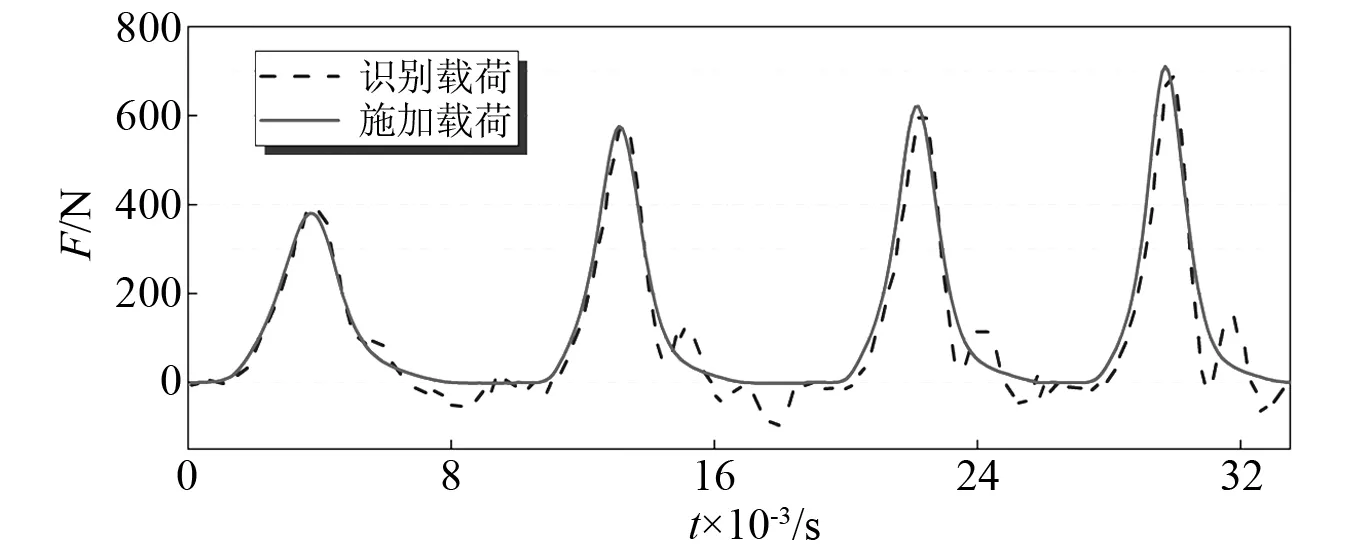
图6 施加载荷与识别载荷对比Fig.6 Comparison between the applied loads and identified loads

综合数值和试验结果可知，基于形函数的冰载荷识别算法具有求解速度较快、稳定性良好及精度较高的优点，适用于船体外板结构动冰载荷识别分析。

4 结 论

实船冰载荷监测工作在国内尚属起步状态，其监测识别算法作为核心技术可直接提升监测的整体水准，进而提高我国冰区舰船的设计建造能力。基于以上研究内容可得出以下结论及研究方向：

(1)本文结合有限元形函数理论、共轭梯度正则化算法和最小二乘问题的终止迭代法则等建立了船体结构动冰载荷快速识别模型，并利用数值和试验手段对模型识别效果进行了检验。结果表明基于形函数载荷识别算法相比于常用的影响系数矩阵法，补充考虑了冰载荷的动力效应；同时相比于Green核函数冰载荷识别算法，求解快速性得到了保障。

(2)本文研究证明了线性形函数方法在描述识别冰载荷时程特征方面具有一定的可行性，而实际中的冰载荷可能会表现出极强的随机特性和离散特性，因此需要更高阶形函数作为基函数以更加准确表征冰载荷时程，提升识别模型普适性。同时，为提升试验评估的全面性，将在冰载荷识别试验增加考虑多源载荷识别、真实海冰试样加载及低温环境。

(3)现有实船冰载荷测试数据均是利用影响系数矩阵法识别的，国内外均未有学者采用动载荷识别算法对其原有认知的冰载荷时空分布特征、峰值分布拟合情况及峰值参数化表征函数等规律进行对比研究。下一步可利用实测数据进行分析，明确原有冰载荷识别算法的缺陷和修正冰载荷谱等统计规律。