基于建模预测与关系规则的养殖水体溶解氧含量调控方法

周新辉 黄 琳 樊宇星 段青玲

(1.中国农业大学信息与电气工程学院，北京 100083；2.中国农业大学国家数字渔业创新中心，北京 100083；3.宁波市海洋与渔业研究院，宁波 315000)

0 引言

工厂化养殖作为未来水产养殖重要的生产模式，其生产效率将直接决定水产养殖的总产量和收益[1-2]。养殖水环境是水产品赖以生存的栖息地，其中水体溶解氧含量是衡量养殖水质的关键水质因子[3-4]。工厂化养殖中，由于养殖密度大，且养殖环境具有封闭性，养殖过程经常面临低氧带来的风险。为了提高溶解氧含量，养殖工厂通常全天开启大功率增氧机，但是这种增氧操作存在能耗过大等问题。因此，构建整套溶解氧控制系统，最大程度优化增氧效果、降低能耗是水产养殖行业主要的目标。

随着工厂化养殖的不断发展，国内外许多学者对溶解氧的调控开展了大量的研究[5-8]。其中，溶解氧最为普遍的调控方法是基于阈值的开关定时控制。这种调控方式需要根据养殖水产品的实际生长需求设定溶解氧含量的阈值区间，如果溶解氧含量低于下限就开启增氧机，高于上限就关闭增氧机。由于曝气增氧过程具有一定的滞后性，如果监测到溶解氧低于阈值时再开启增氧机，短时间内溶解氧含量不能达到设定值，仍然会对养殖生物造成一定损害。因此，建立溶解氧预测模型，对未来溶解氧含量进行预测，提前指导增氧机进行相关动作是基于阈值的开关定时控制最为关键的环节。目前，溶解氧含量预测已经被广泛研究，许多成熟的预测模型被开发出来，普遍使用的模型主要包括BP神经网络[9-10]、极限学习机[11]和支持向量机[12]等。基于阈值的开关定时控制虽然可以在一定程度上减少了能源消耗，避免了低氧导致的养殖风险问题，但是无法满足溶解氧高精度控制的要求。

针对开关定时控制的多种缺点，学者提出了基于智能控制算法的溶解氧精准控制方法。首先需要搭建溶解氧控制系统硬件平台，然后确保系统各个硬件之间能够保持良好的通信，最后智能控制算法根据溶解氧实际值与理想设定值的偏差对增氧机进行反馈控制，调节增氧机工作功率，让溶解氧始终保持在理想设定值范围内。目前，一些单一的智能控制算法，如模糊控制[13-14]和PID控制[15]是水产养殖溶解氧调控中最常用的两种控制器。然而，由于水产养殖环境复杂多变，这些单一的控制器参数不能在线调整，在溶解氧控制精度上仍存在一些不足。针对这一缺点，学者提出了一些混合的自适应PID控制器，如模糊-PID控制[16]、BP-PID[17]和RBF-PID[18]控制器。该类控制器可以利用模糊规则或者神经网络对PID的3个控制参数进行在线调整，以满足复杂多变的水产养殖溶解氧的控制需求，使溶解氧含量始终维持在理想范围内。基于智能控制算法的反馈控制虽然能够满足溶解氧控制高精度的需求，提升了水产养殖的自动化程度，但是对养殖硬件设施的要求很高，极大增加了养殖成本，不利于推广使用[19]。

基于此，本文综合上述2种溶解氧调控方式的优点，提出一种基于建模预测与关系规则库的溶解氧精准调控方法。首先构建自适应增强的粒子群优化极限学习机(AdaBoost-PSO-ELM)预测模型，实现对溶解氧含量准确预测；然后进行曝气增氧实验，探索溶解氧初始质量浓度、曝气流量和增氧机开启时间三者之间相互作用关系，制作成增氧机控制规则库；最后，将溶解氧含量的预测模型与增氧机控制规则库进行结合，以期合理控制增氧机的开启时间与功率，起到节能增效的目的。

1 研究方法

1.1 数据采集与预处理

以浙江省宁波市海洋与渔业研究院养殖基地为实验场地，搭建了一个小型循环水养殖系统，如图1所示。该系统包括全自动增氧机、微孔曝气设备、循环水泵、水质传感器和远程水质无线监控系统等。养殖水缸为一个圆柱形容器，其半径为0.75 m，水深为0.8 m。通过计算，养殖水体体积约为1.4 m3。养殖品种为南美白对虾，约500尾。

图1 搭建的循环水养殖实验系统Fig.1 Established circulating water aquaculture system

本文的数据采集方式包括手动采集和自动采集2种方式。手动采集的数据为曝气增氧数据，自动采集的为水质数据。增氧数据采集过程中，采用鼓入氮气的方式将溶解氧降低到不同的初始质量浓度，然后再进行曝气增氧实验，记录数据。增氧机微孔气头置于养殖水缸底部中央位置。另外，水缸中部署了多种水质传感器，置于水缸底部边缘位置，通过物联网平台自动采集水质数据。由于养殖水缸搭建在室内，受环境因素影响小，且水体体积较小，可认为溶解氧在水缸空间内呈均匀分布。采集的数据信息如表1所示。

表1 采集数据信息Tab.1 Collected data information

图3 预测算法流程图Fig.3 Flow chart of forecast algorithm

实验时间为2020年9月3—22日，共采集2 908条数据。其中，前2 650条为模型训练集，后258条为测试集。系统采集数据时，由于受到网络波动等影响，会造成采集的数据存在异常值和缺失值[20]。采用线性插值法对异常值进行处理，采用均值填充法对缺失值进行处理。

1.2 溶解氧调控方法总体流程

本文提出了一种基于建模预测与关系规则库的溶解氧含量精准调控方法，其总体流程如图2所示。

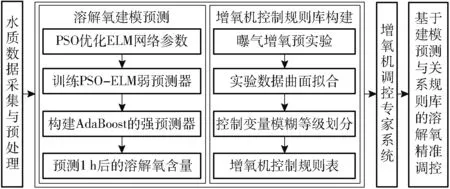
图2 方法的总体流程图Fig.2 Overall flow chart of proposed method

(1)溶解氧预测。采集水产养殖水环境数据，如溶解氧质量浓度、水温、pH值和盐度等，构建AdaBoost-PSO-ELM溶解氧预测模型，预测未来溶解氧含量。

(2)规则库构建。进行溶解氧增氧预实验，对溶解氧初始质量浓度、曝气流量和增氧机开启时间进行量化，构建增氧机控制规则表。

(3)溶解氧调控。将关系规则库和预测模型嵌入计算机监控中心，得到增氧机调控专家系统，专家系统根据溶解氧含量的预测值(如果低于设定阈值)，并结合当前溶解氧含量，调用控制规则表，合理指导增氧机的开启时间与功率。

1.3 自适应AdaBoost-PSO-ELM强预测模型

AdaBoost算法可以将多个弱预测器组合成一个强预测器，用于提升模型的预测精度[21]。本文提出的AdaBoost-PSO-ELM算法基本思想是：首先初始化一个ELM基学习器；然后反复迭代训练得到多个ELM弱预测器，每次迭代中，对预测误差较大的样本进行加大权重，对其进行重点学习，实现“优中选优”；最后结合AdaBoost算法将多个弱预测器通过加权组合成一个强预测器，进一步提高ELM网络的预测准确率。基于AdaBoost的强预测器算法流程如图3所示。

AdaBoost-PSO-ELM算法的详细步骤为：

(1)ELM网络初始化。对于给定输入样本，首先确定ELM网络结构，并对网络相关参数进行初始化，ELM网络结构如图4所示。

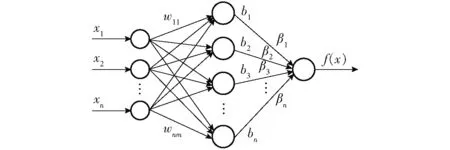
图4 极限学习机的网络结构Fig.4 Network structure of extreme learning machine

ELM网络结构中，输入向量X=(x1,x2,…,xn)，代表传感器采集的各种水质数据，例如溶解氧质量浓度、水温、pH值和盐度等。隐含层偏置B=(b1,b2,…,bn)和输入权值W=(w11,w12,…,w1m,w2m,…,wnm)的初值是在模型训练时随机给定的。输出向量β=(β1,β2,…,βn)由输入向量X、输入权值W和隐含层偏置B共同决定。

(2)初始化样本分布权值。从样本空间选择m组数据，初始化每一个输入样本的分布权值

(1)

(3)PSO-ELM弱预测器预测。通过PSO算法对ELM网络初始参数进行优化，得到多个ELM弱预测器；在训练第n个ELM弱预测器时，采用训练集数据进行训练，得到预测序列的预测误差和Serror，计算公式为

(2)

(4)计算预测序列权重。根据预测序列的Serror计算序列的权重，n为弱预测器PSO-ELM编号，相应的权重an计算公式为

(3)

(5)权值更新。根据式(3)对第n+1个弱预测器的样本权值进行调整，重点对上一个弱预测器中预测误差较大的样本进行调整，即对预测误差较大样本的权值进行加重，适度降低预测准确的样本的权值，调整公式为

(4)

式中yn——溶解氧质量浓度实际值

fn(xi)——第n个弱预测器第i个样本的预测值

Dn——第n个弱预测器的分布权值

Zn——归一化因子，其作用是使所有分布权值之和为1

(6)输出强预测器函数。经过n次迭代后，得到第n个弱预测器的函数为fn(x)，相应的n个弱预测器的权重集合为{a1,a2,…,an}，将n个弱预测器加权组合，可得到的强预测器函数Y(x)，表达式为

(5)

式中 sign()——符号函数

1.4 基于多项式拟合的增氧机控制规则库建立

水产养殖曝气增氧过程中，增氧能力主要与养殖生物品种、养殖密度、水体体积、曝气流量和溶解氧浓度有关。实验过程中，养殖品种、养殖密度和养殖水体短时间内不会发生巨大变化，因此，曝气流量是溶解氧调控过程的主要操控变量。相关研究指出，水体溶解氧质量浓度越高，增氧效率就会越低，当水体溶解氧达到饱和时，增氧效率基本为零[22]。为了提高能源利用效率，针对本文的溶解氧含量调控模式，对增氧能力进行精确量化，构建规则库是实现溶解氧含量合理调控的前提。

关系规则库构建是增氧机控制的关键部分，需基于溶解氧增氧初始浓度、曝气流量和增氧机开启时间之间的量化结果。关系规则库的构建主要分为3个步骤：

(1)进行增氧实验，掌握不同曝气流量下的溶解氧响应规律。

(2)设置一个理想的溶解氧质量浓度，进行曝气实验，并记录增氧初始质量浓度和溶解氧达到理想值时增氧机的开启时间。将记录的数据导入Matlab拟合工具箱，选择最小二乘拟合法和多项式先验方程对三者之间的相互作用关系进行量化。

以一元线性拟合为例，最小二乘法的最优拟合原理是使采样点与被拟合直线之间的距离平方和最小，具体公式为

(6)

式中a、b——代求系数yt——拟合值

xt——实际值

多变量的曲面拟合数学方程式有多项式函数和傅里叶级数2种形式，其中最常用的是多项式函数形式。因为多项式能够逼近任何连续函数，因此，用多项式作为多变量拟合的先验方程，能够精确反映出变量之间的非线性关系。目前，常用的多项式形式为：

二次多项式

z=a0+a1x+a2y+a3x2+a4xy+a5y2

(7)

三次多项式

z=a0+a1x+a2y+a3x2+a4xy+a5y2+a6x3+
a7x2y+a8xy2+a9y3

(8)

式中z、x、y——变量

a0～a9——待定常量

(3)为了合理地制定控制规则，减少计算量，首先需要基于多项式的量化结果，对3个变量(曝气流量、溶解氧初始质量浓度、增氧机开启时间)进行模糊等级划分。然后，结合实际的养殖系统情况和专家经验，归纳总结得出合理的增氧机控制规则库。

1.5 溶解氧预测模型与规则库的联合调控原理

本文提出的溶解氧调控方法主要包括溶解氧含量建模预测和关系规则库构建。溶解氧建模预测主要对未来时刻溶解氧含量进行预测，提供溶解氧含量变化的先验曲线。关系规则库制定了不同溶解氧质量浓度下的增氧机开启方式(时间与功率)，为溶解氧合理调控提供基础。

在养殖水质监控平台中，溶解氧预测模型根据传感器采集的水质数据对未来时刻溶解氧含量进行预测，如果预测值低于设定的安全阈值，增氧机控制专家系统会调用规则库，并结合当前时刻的溶解氧含量，通过查表的方式输出增氧机调控方式，即最优的增氧机开启时间和开启功率。基于溶解氧建模预测与规则库的溶解氧调控流程如图5所示。

图5 溶解氧调控整体流程图Fig.5 Overall process of dissolved oxygen regulation

1.6 性能评价指标

本文采用决定系数(Coefficient of determination,R2)、误差平方和(Sum of squares due to error,SSE)、平均绝对误差(Mean absolute error,MAE)、均方误差(Mean squared error,MSE)以及均方根误差(Root mean squared error,RMSE)评估预测模型和曲面拟合的准确性。一般情况下，决定系数绝对值越接近于1，拟合精度越高；其余指标值越小，模型预测精准度越高[23-24]。

2 试验与结果分析

2.1 基于Adaboost-PSO-ELM的溶解氧含量预测结果

为避免ELM网络参数随机化，利用PSO算法寻优得到ELM的最优输入权值和隐含层偏置。PSO参数设置：种群规模为25，最大迭代次数为100，最大惯性权重为0.8，最小惯性权重为0.4，最大速度为1，最小速度为-1，学习因子分别为2.4和1.6。在PSO迭代过程中，本文以溶解氧质量浓度实际值与预测值均方误差(MSE)作为粒子寻优的目标函数，迭代次数与均方误差的关系曲线如图6所示。

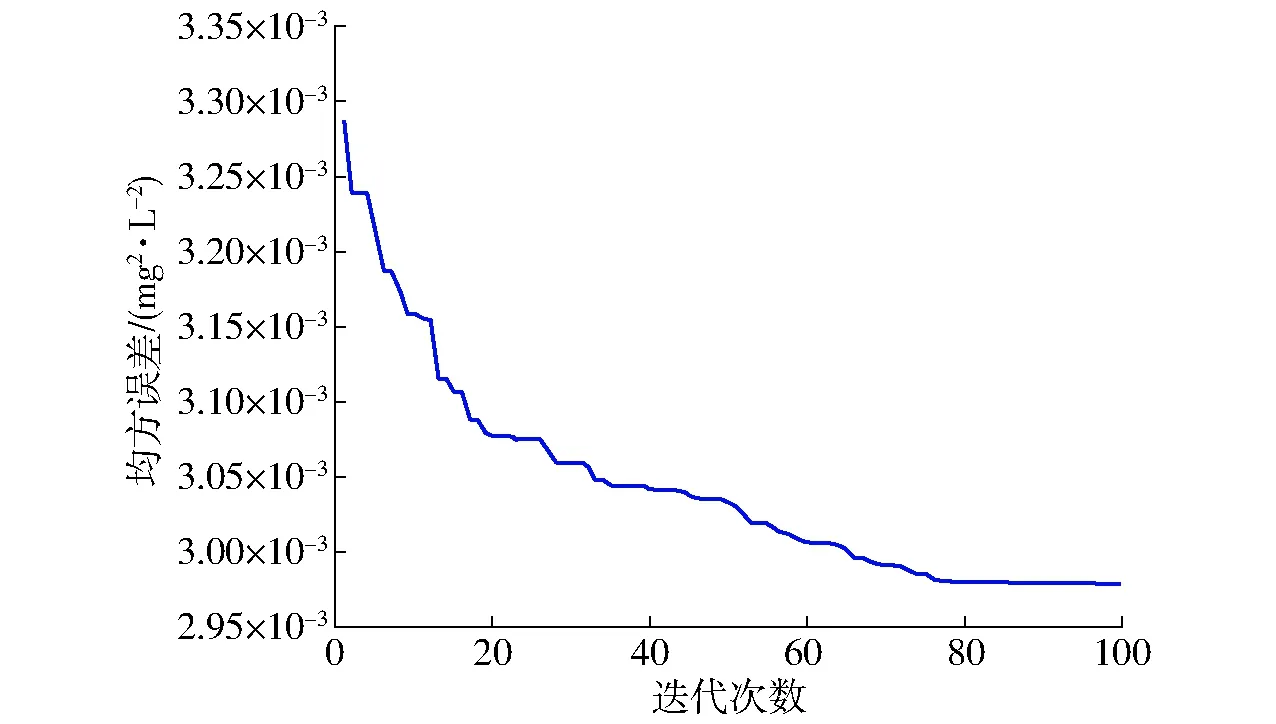
图6 PSO寻优过程的均方误差Fig.6 Mean square error of PSO optimization process

从图6中可以看出，在迭代的初始时刻，粒子种群的收敛速度很快，均方误差迅速下降。随着迭代次数的增加，粒子种群的收敛速度趋于平缓，当PSO在寻优过程中迭代到80次左右时，均方误差已不再下降，此时得到最优解。将获得的最优网络权值和偏置输入ELM网络训练溶解氧预测模型。

为了说明本文提出的模型有更优越的预测性能，将AdaBoost-PSO-ELM的预测结果分别与PSO-ELM、ELM、BPNN和WNN模型进行对比，以MSE、MAE和RMSE作为模型性能的评价指标。AdaBoost-PSO-ELM采用PSO优化后的权值和隐含层偏置作为网络输入参数，选择“sigmoid”函数作为网络的激活函数。实验中，所有的预测模型运行都是基于Matlab 2014a环境。本文使用同一批水质数据集，以预测1 h后的溶解氧含量为例，5种模型对溶解氧质量浓度的预测结果见图7。

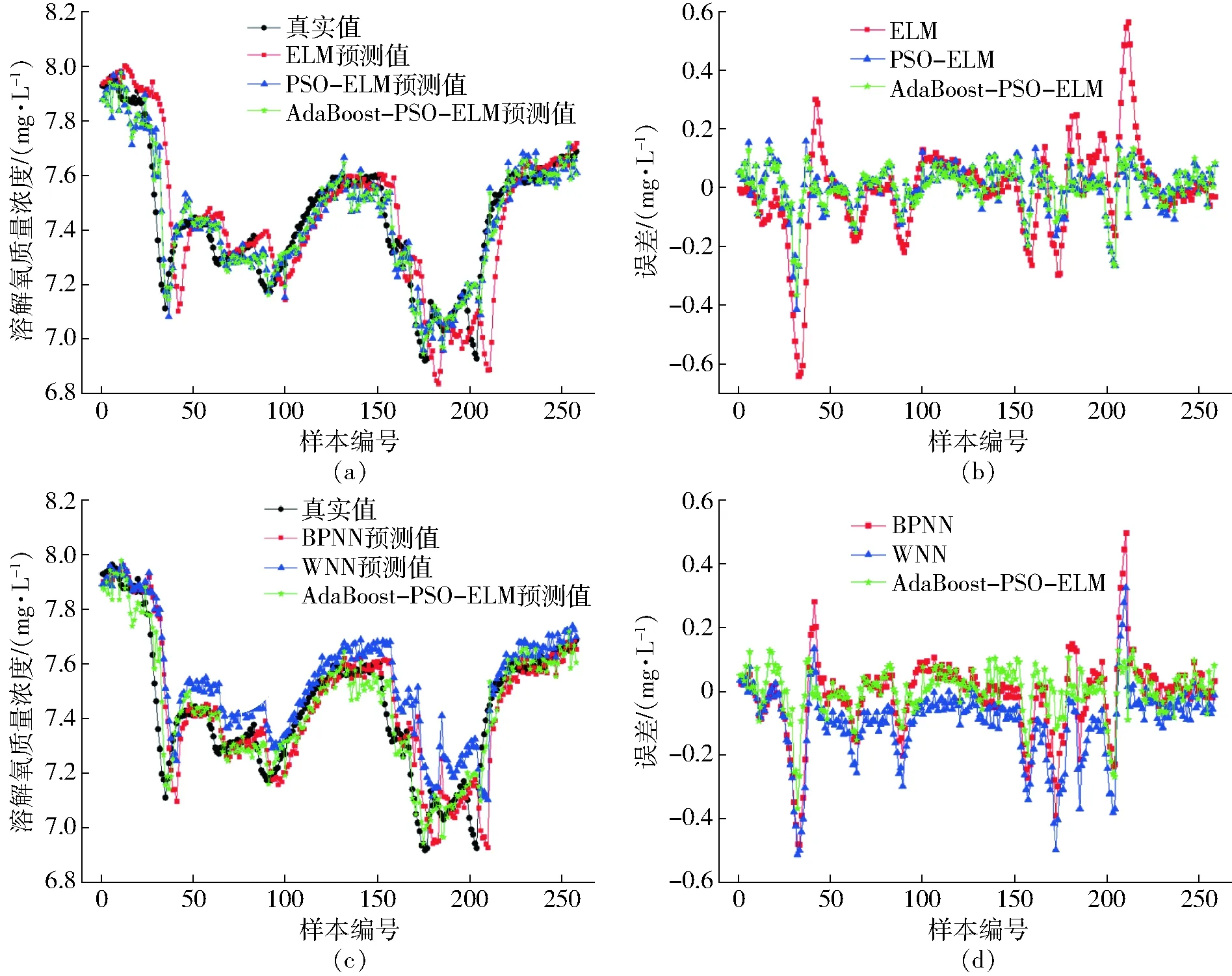
图7 不同模型的溶解氧预测结果Fig.7 Dissolved oxygen prediction results of different models

从图7a可以看出，ELM的预测效果最差，溶解氧含量预测值与真实值偏差较大。当使用PSO对ELM的网络初始参数进行优化以后，ELM的预测效果得到极大改善。在PSO-ELM预测模型的基础上，构造由3个PSO-ELM组成的弱预测器，然后采用AdaBoost算法将3个PSO-ELM弱预测器组成1个强预测器，再次对溶解氧含量进行预测。预测结果表明，相较于PSO-ELM模型，AdaBoost-PSO-ELM模型再次提升了预测精度。从图7c可以看出，AdaBoost-PSO-ELM模型的预测效果远远优于BPNN和WNN模型。从图7b、7d可以明显看出，AdaBoost-PSO-ELM模型的预测误差偏离零线最小，也说明本文提出的模型有更高的预测精度。5种预测模型的评价指标见表2。

从表2可以看出，在5种模型中，AdaBoost-PSO-ELM的各种预测性能评价指标值MSE、MAE和RMSE，均为最小，表示其性能最优。结果说明AdaBoost-PSO-ELM模型的预测精度相比于其它4种模型提高很大。

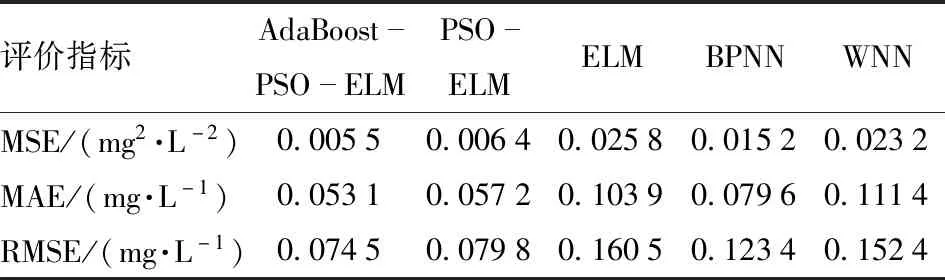
表2 5种预测模型的评价指标Tab.2 Evaluation indicators of five prediction models

2.2 增氧机控制规则库构建结果

在已搭建的循环水养殖系统中，进行多组不同曝气流量下的溶解氧增氧预实验，记录溶解氧质量浓度随时间的变化曲线，如图8所示。

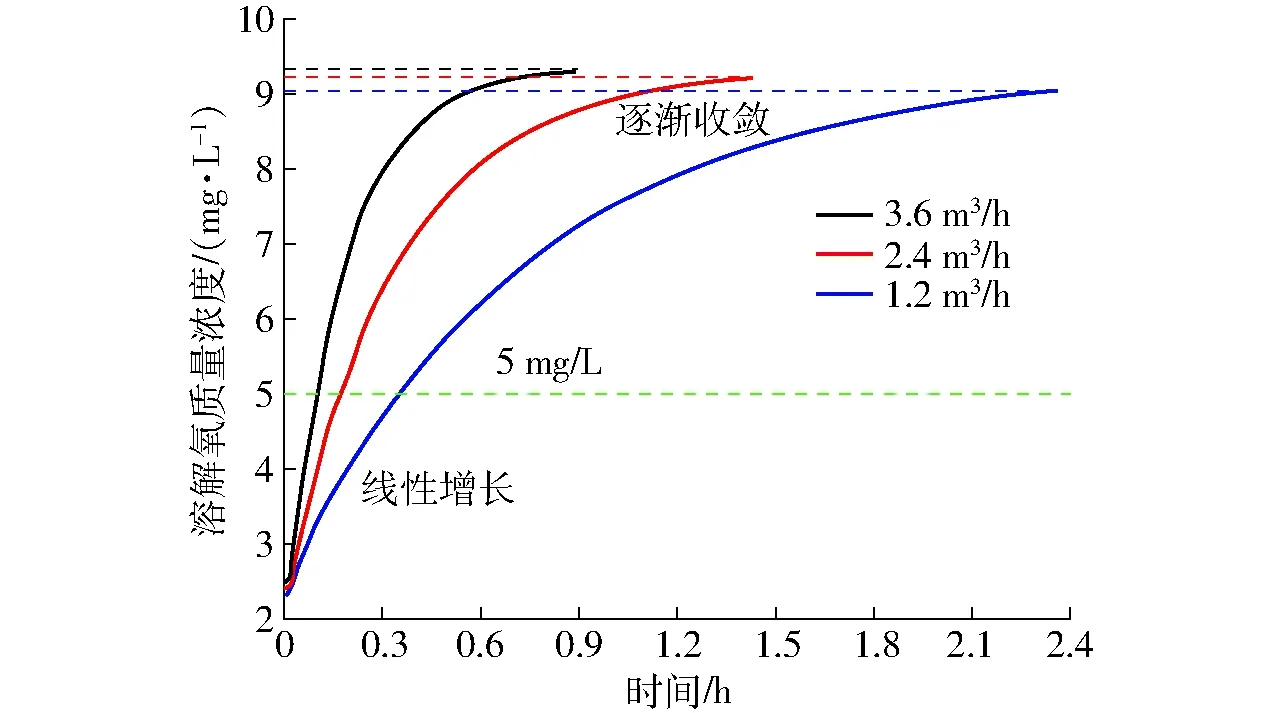
图8 不同曝气流量下的溶解氧增氧响应曲线Fig.8 Dissolved oxygen aeration response curves at different airflow rates

从图8中可以看出，当水体溶解氧质量浓度较低时(5.0 mg/L以下)，其上升速度比较快，基本呈线性增长，说明增氧效率比较高。当水体溶解氧质量浓度较高时，增氧曲线逐渐收敛，增氧效率开始下降。当溶解氧达到饱和时，无论曝气流量多大，增氧效率基本为零。因此，结合溶解氧增氧响应规律，本文探索曝气流量、溶解氧初始质量浓度与增氧机开启时间之间的相互作用关系，为合理控制增氧机提供科学依据。

溶解氧质量浓度设定值根据实际情况设置，可以为溶解氧饱和质量浓度，也可以为养殖生物生长的最适质量浓度。本文以溶解氧质量浓度设定值为6.0、8.6 mg/L(饱和质量浓度)为例，选择4种不同曝气流量(0.9、1.8、2.7、3.6 m3/h)在不同溶解氧初始质量浓度下进行增氧实验，记录溶解氧达到设定值时增氧机的开启时间，根据记录的数据，分别选择二次多项式和三次多项式作为先验公式进行拟合，得到三维关系曲面图，如图9所示。

图9 基于不同多项式的增氧能力拟合曲面Fig.9 Fitting surface graphs of aeration capacity based on different polynomials

从图9中可以看出，当溶解氧初始质量浓度越低，曝气流量越小，溶解氧质量浓度达到设定值所需的时间就越长。在相同曝气流量下，溶解氧初始质量浓度越高，到达设定值时，增氧机开启时间就越少。在相同初始溶解氧质量浓度下，曝气流量越大，到达设定值时，增氧机开启时间就越少。基于2种多项式的拟合结果如表3所示。

从表3可以看出，基于三次多项的拟合指标值均优于二次多项式。因此，为了提高控制精确度，本文选择三次多项式对增氧能力进行精确量化，结果如图9b、9d所示。其中，图9b中标出的坐标点表示，当溶解氧初始质量浓度为2.847 mg/L，在曝气流量为3.116 m3/h的持续作用下，养殖水体溶解氧质量浓度达到6.0 mg/L时，增氧机需要开启0.137 3 h。图9d中标出的坐标点表示，当溶解氧初始质量浓度为5.412 mg/L，在曝气流量为2.931 m3/h的持续作用下，养殖水体溶解氧质量浓度达到8.6 mg/L时，增氧机需要开启0.661 1 h。结果表明，曝气流量、溶解氧初始质量浓度与增氧机开启时间的关系已被精确量化。

表3 各种情况的拟合度评价指标Tab.3 Evaluation index of goodness of fit in various situations

根据三次多项式的量化结果，构建增氧机开启时间控制关系规则库。以溶解氧达到饱和质量浓度时(8.6 mg/L)为例，根据现场实验数据和养殖经验，将曝气流量划分为4个等级[QS,QM,QB,QL]，分别代表[1.0，2.0，3.0，4.0] m3/h；将溶解氧质量浓度划分为7个等级[DS,DM,DB,DL,DX,DY,DZ]，分别代表[0～1.5，1.5～3.0，3.0～4.5，4.5～6.0，6.0～7.5，7.5～9.0，>9.0] mg/L；将增氧机的开启时间划分为8个等级[TC,TS,TM,TB,TL,TX,TY,TZ]，分别代表[0，0.1，0.3，0.6，1.0，1.5，2.0，2.5]h。针对本文循环水养殖系统的增氧特点，并结合实际养殖经验，可以归纳总结得出增氧机控制的经验规则共28条，如表4所示。

表4 增氧机开启时间控制规则表(1.4 m3水体)Tab.4 Control rules for working time of aerator (1.4 m3 water body)

2.3 基于增氧机控制专家系统的溶解氧调控结果

将本文训练的溶解氧预测模型和构建的增氧机控制规则表写入计算机监控中心可得到增氧机控制专家系统。专家系统可根据溶解氧预测值，通过制定的规则表，合理地向增氧机发送控制指令，实现溶解氧的合理调控。

根据表4的结果可知，当溶解氧处于较高等级时，如“DY”，优先让增氧机以较小气量(QM,QS)短时开启，较大气量(QL,QB)时不开启，尽量减少噪声对水产品产生的影响。当溶解氧处于最低等级时，如“DS”，则优先以较大气量(QL)曝气增氧，尽快提升水体溶解氧含量，避免缺氧现象发生。增氧机控制规则触发时，专家系统优先以当前溶解氧含量决定增氧机曝气流量，然后根据二者数值通过查表推断出增氧机的开启时间。

从以上叙述中可以看出，将溶解氧建模预测与增氧机控制规则库结合起来可实现溶解氧含量的合理调控。在此基础上，已制定的增氧机控制规则库也可以为溶解氧自动控制和手动控制提供依据。

2.4 讨论

基于AdaBoost的强预测器模型能够根据预测误差调整若干组弱预测器的权重，能够把PSO算法随机选择交叉、变异优化后的ELM模型的不同预测结果组合起来，实现AdaBoost强预测器“优中选优”的优点，相较于ELM、PSO-ELM和传统的神经网络模型，不仅大幅度地改善了溶解氧含量的预测精度，同时也提升了模型的泛化能力。

本文通过进行不同曝气流量下的增氧预实验，对增氧机的增氧能力进行了量化，得出了增氧机开启时间与溶解氧质量浓度以及曝气流量之间的非线性关系，并结合实际养殖经验，总结制定了一系列增氧机控制规则。但是由于实验条件限制，所使用的增氧机型号较小，本实验结论仅适应于小型鱼缸养殖，后期工作应该对大型养殖水池进行探究。

传统的溶解氧调控通常面临控制精度不高，且能源损耗过大等问题，而本文提出的溶解氧调控方法将溶解氧含量预测模型与自建的经验规则库结合起来，不仅避免了基于阈值调控增氧滞后的问题，而且对系统整体硬件设施要求不高，有很大的应用前景。但是本文结论仅在实验室理想条件下实验得到，还没有在实际现场应用验证，后期工作应进行实际养殖工厂中的应用，以检验其可靠性。

3 结论

(1)通过采集溶解氧质量浓度、水温、pH值和盐度4种水质因子作为模型的输入变量，训练AdaBoost-PSO-ELM预测模型，能够对1 h后的溶解氧含量进行准确预测。与PSO-ELM、ELM、BPNN和WNN模型相比，本文提出的模型有更高的预测精度，其评价指标MSE、MAE和RMSE均为最小，分别为0.005 5 mg2/L2、0.053 1 mg/L和0.074 5 mg/L。

(2)在循环水养殖系统增氧预实验中，增氧机开启时间与曝气流量、溶解氧初始质量浓度之间的非线性关系明显。基于此结果，采用三次多项式作为先验方程对增氧能力进行了精确量化，阐明了三者之间的相互作用数学关系，并制作成增氧机控制关系规则表，为合理控制增氧机开启时间与开启功率提供依据。