桑园土壤非等径颗粒离散元仿真模型参数标定与试验

宋占华 李 浩 闫银发 田富洋,3 李玉道,4 李法德

(1.山东农业大学机械与电子工程学院，泰安 271018；2.山东省园艺机械与装备重点实验室，泰安 271018；3.山东省农业装备智能化工程实验室，泰安 271018；4.农业生产机械装备国家工程研究中心，泰安 271018)

0 引言

在蚕桑高效生产中，桑园管理占有重要地位。桑园管理中的松土、施肥等作业，由于没有适合的作业机具，目前主要靠人工或微耕机进行作业，劳动强度大，作业效率低，因此，目前急需适合桑树栽植模式的桑园松土施肥机械。在土壤耕作机械研发中，利用离散元仿真软件研究土壤在切割、翻垡、开沟等过程中的颗粒群离散及动态破裂、破碎和流动，有助于了解土壤与作业部件的相互作用过程，为作业部件的优化设计提供依据[1-2]。

在农业土肥秸秆特性研究方面，目前已有研究学者对颗粒肥料[3]、散体厩肥[4]、作物残茬等[5-9]进行了离散元参数标定研究。运用离散元法进行机械触土部件作业仿真时，桑园土壤的本征参数包括密度、泊松比和弹性模量等，可通过查阅文献或试验测得；而土壤颗粒间及土壤和触土部件间的接触参数包括静摩擦因数、滚动摩擦因数和碰撞恢复系数，较难直接测得[10]。目前，有研究学者应用试验与离散元仿真相结合的方法完成了沙土、砂壤土、黏壤土、黑土区玉米秸秆-土壤混料等的接触参数标定[10-14]。

为节约建模和仿真运算时间，现有针对土壤颗粒离散元模型参数标定的研究，多采用放大尺寸的等直径球形颗粒替代真实土壤，仿真所用颗粒直径为真实土壤颗粒直径的10～50倍，张锐等[11]选用土壤颗粒半径为1 mm，方会敏[15]选用土壤颗粒半径为5 mm，丁启朔等[16]选用土壤颗粒半径为8 mm。然而，仿真所用土壤粒径对建模精度和建模效率有重要影响，采用过大的土壤颗粒易导致仿真结果的误差增加，反之，计算机的运算时间急剧增加[14]。另外，采用等直径的球形土壤颗粒无法充分体现实际土壤的粒径分布对土壤-土壤颗粒和土壤-触土部件间相互作用的影响[14,17]。因此，有研究学者采用非等直径颗粒对土壤模型和土壤-触土部件接触模型参数进行了标定，UCGUL等[18]选定土壤颗粒直径范围为7.5～118 mm；SUN等[19]选用的土壤颗粒半径范围为4～6 mm；BARR等[20]选用土壤颗粒半径为2～3 mm。

综合考虑仿真准确性及计算机计算能力，本文拟在对真实土壤粒径及其分布分析的基础上，以非等直径球形颗粒作为土壤颗粒模型，基于试验与离散元仿真模拟相结合的方法，以国家和山东省蚕桑产业技术体系试验示范基地的桑园土壤为研究对象，触土部件为65Mn钢材料，提出一种通过试验与仿真模拟相结合标定桑园土壤颗粒接触参数的方法，以期为桑园土壤与触土部件的离散元仿真参数设置提供参考。

1 土壤特性参数测量

1.1 试验材料

桑园土壤于2019年3月取自山东省泰安市岱岳区马庄镇朱家寨村国家和山东省蚕桑产业技术体系蚕试验示范基地(35.96°N，117.01°E)。桑园桑树品种为育71-1，树龄6年，土壤类型为砂壤土，pH值为7.7，年均降雨量720 mm。

1.2 试验方法

土壤特性参数试验参照国标GB/T 50123—1999《土工试验方法标准》进行。

1.2.1基本物理参数测量方法

(1)土壤粒径分布试验

在面积为1.3 hm2的桑园内，采用五点法取桑园土层0～400 mm的土壤样本，每个样点取样质量大于2 kg，取样后待土壤自然风干后，用电子天平(精度0.001 g，JA5003A型，上海精天电子仪器有限公司)分别称量各样点土壤样本500 g，准确至0.1 g，利用电动振筛机(8411型，绍兴市上虞区道墟越州土工仪器厂)和试验标准筛(孔径分别为2、1、0.5、0.1、0.05 mm)进行筛分，振筛时间为10 min。振筛结束后，称量各级土壤筛及底盘内的土壤质量，准确至0.1 g[21]。

(2)土壤密度及含水率试验方法

采用五点法确定取样位置，每个取样点分4层取样，每层深度为100 mm。采用环刀法测定土壤密度。取样时将样点周围清理干净，在取土环刀(内径50.46 mm，高度50 mm)内壁均匀涂抹凡士林，环刀刃口垂直于土壤平面放置，将手柄置于环刀上方，用锤子敲击手柄使环刀切入土壤。待环刀没于土壤平面，清除环刀周围土壤，将环刀轻轻取出，用刮土刀刮掉多余土壤，使环刀两端土壤平整。为防止土壤水分蒸发，立即将清理好的土样放置在电子天平上称量，称量后将土样放置在铝盒内，采用干燥法测量土壤含水率。

1.2.2土壤休止角测量

试验土样取自3个长×宽为200 mm×200 mm的随机样点，自取样点土壤表面开始，每向下100 mm作为1个取样层，每个样点平均分为4层分别取样，取土深度累计为400 mm。每层试样取完后用密封袋分别密封并标号，在实验室进行试验。通过漏斗法测量土壤从漏斗中漏出后所形成的锥体母线与水平面的夹角，测量原理如图1所示，图中θ即为休止角。

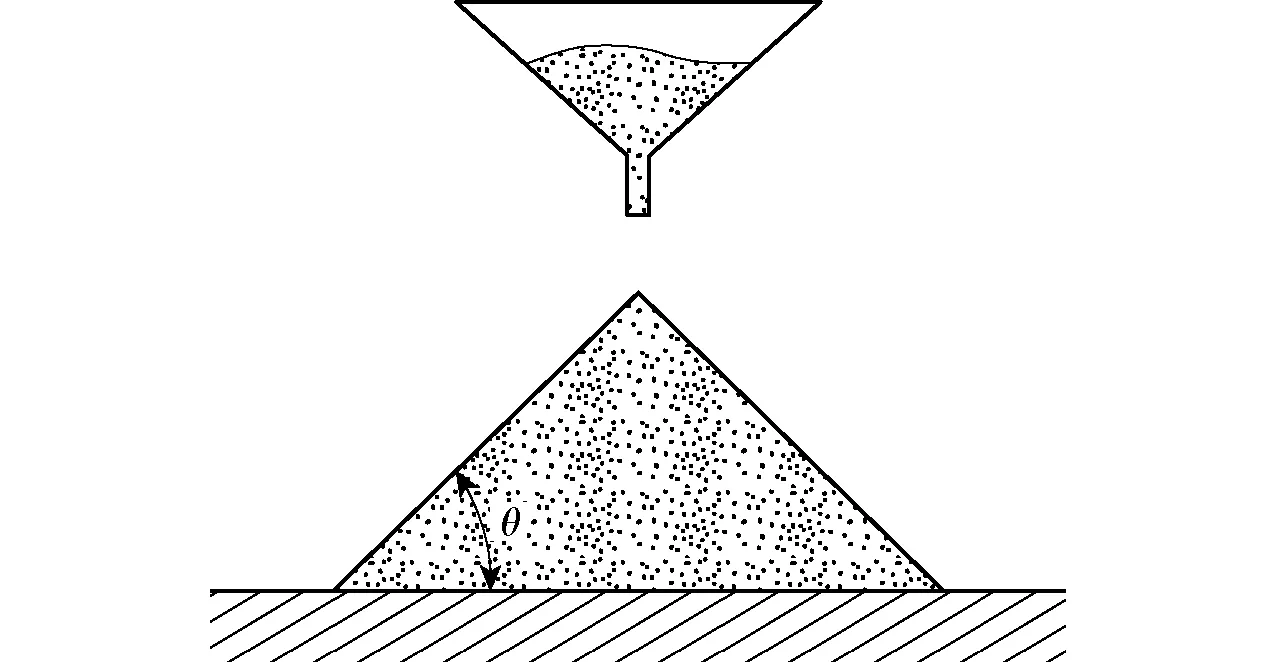
图1 休止角测量原理Fig.1 Measuring principle of repose angle

采用智能粉体特性测试仪(BT-1001型，丹东百特仪器有限公司)测定土壤休止角，漏斗锥角为120°，流出孔内径为13 mm，流出口底沿与接料盘盘面距离为80 mm，料盘直径为80 mm。如图2所示，试验时，启动智能粉体特性测试仪，将土壤试样从仪器顶部通过筛网缓慢倒入漏斗中，土壤逐渐从漏斗出料口流出，在圆盘上堆积，当接料盘下方托盘出现少量土壤时即停止向漏斗内添加土壤试样，待漏斗内的土壤完全落下后，按下智能粉体特性测试仪的完成按键，智能粉体特性测试仪通过成像系统自动计算并输出土壤休止角。

图2 土壤休止角测定Fig.2 Repose angle of soil measurement1.摄像头 2.漏斗 3.接料盘

1.2.3土壤-65Mn钢滑动摩擦角测量

土壤滑动摩擦角测量试验所用仪器为斜面仪(自制)，摩擦面材料为农机具触土部件常用的65Mn钢。将所取土样在电子天平上称量200 g，准确至0.1 g，称量完毕的土样加入放置在水平摩擦面上的试样盒(内部长×宽×高为100 mm×100 mm×100 mm)内，将试样盒稍微抬离摩擦面，确保试样盒壁面不接触摩擦面；缓慢匀速转动手柄，使摩擦面一端缓慢上升，避免振动。如图3所示，当土壤试样开始向下滑动时，记录此时的摩擦面倾角，即为土壤滑动摩擦角。

图3 土壤滑动摩擦角测定Fig.3 Sliding friction angle of soil measurement

1.2.4直剪试验及内摩擦角测量

采用五点法取土壤直剪试验试样，利用取土环刀(内径61.8 mm，高度20 mm)在每个样点深度100、200 mm分别取样一次，将试样与环刀共同放入环刀盒并密封保存。利用等应变直剪仪(ZJ-1型，南京土壤仪器厂)进行直剪试验测定土壤的抗剪强度τs、内摩擦角φ及内聚力c。土壤抗剪强度是指在外力作用下，土壤抵抗破坏的极限剪应力，通常可用库伦公式[22]表示为

τs=c+σtanφ

(1)

式中σ——法向压应力

利用等应变直剪仪分别在σ为100、200、300、400 kPa作用下，测出土壤剪切破坏时所需的剪应力τ。利用相应的τ与σ绘制τ-σ抗剪强度线。内摩擦角φ通过强度线的斜率k计算，即φ=arctank。

图4为试样被剪切破坏后的形状。

图4 剪切破坏后的土壤样本Fig.4 Soil sample after shear failure

1.3 试验结果

1.3.1基本物理参数

经统计计算后，土壤粒径分布如表1所示。经测定，试验地土壤平均干密度为1.6×103kg/m3，平均湿基含水率为12.56%，平均湿密度为1.79×103kg/m3，表2为土层0～400 mm的土壤密度及含水率。

表1 试验地土壤粒径分级及对应的质量分数Tab.1 Size classification and mass fraction of soil

由表2可知，土壤含水率随着取土深度的增加而减小，这可能是因为试验地进行喷灌作业，导致土壤表层含水率增加，而水分未渗透到深层土壤造成的。土壤干密度随深度变化不明显，除土层0～100 mm内土壤干密度较小，土层100～400 mm内土壤干密度基本相同，这可能是因为桑园耕整作业导致表层土壤干密度减小。

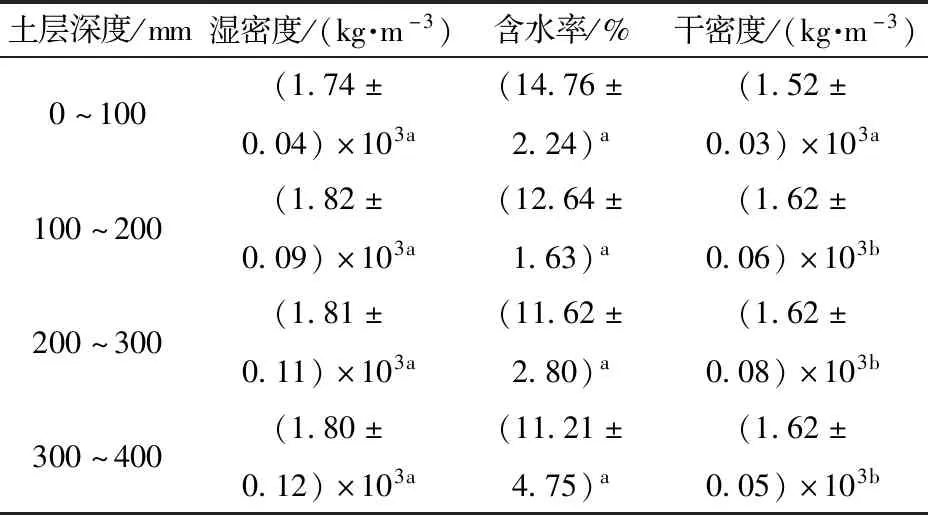
表2 土壤密度及含水率Tab.2 Density and moisture of soil

1.3.2休止角和滑动摩擦角

土壤休止角和滑动摩擦角测定结果如图5所示，在土层0～400 mm中，土壤休止角和土壤与65Mn钢之间的滑动摩擦角随取土深度的增加而增大，且在土层300～400 mm内较土层0～300 mm内增加明显，原因是土层300～400 mm包括犁底层中下部和心土层的土壤，土壤粘性更大，颗粒细而密实，颗粒间更易产生粘结作用而不易碾散，导致土壤休止角和土壤与65Mn钢之间的滑动摩擦角较大。

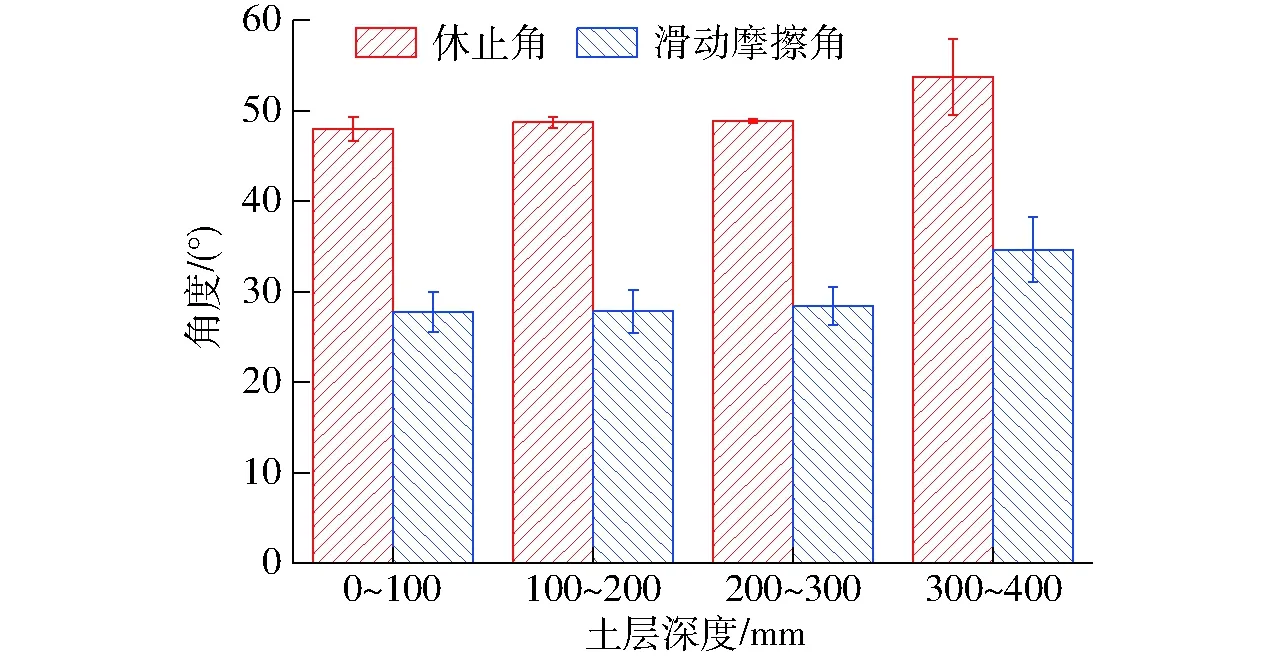
图5 土壤休止角和滑动摩擦角Fig.5 Repose angle and sliding friction angle of soil

1.3.3直剪试验及内摩擦角

土壤直剪试验中，直剪仪所测试样的剪应力τ为

τ=C0R

(2)

式中C0——量力环标定系数，取154.362 kPa/mm

R——量力环测微表最大读数，mm

根据对应的剪应力τ和法向压应力σ绘制抗剪强度曲线，并求出内聚力c和内摩擦角φ。因试验地耕整深度普遍在土层0～200 mm内，因此只对土层0～200 mm进行了直剪试验。计算得到土壤的剪应力如表3所示。

表3 剪应力测试结果Tab.3 Testing result of shearing stress

依据表3数据，绘制土壤抗剪强度曲线如图6所示，土层100 mm的内聚力和内摩擦角分别为1.544 kPa和31.69°，土层200 mm的内聚力和内摩擦角分别为5.403 kPa和32.33°。造成差异的原因是试验地桑园长时间浅耕，导致土层200 mm的土壤因未得到充分耕作更加坚实，土壤密度大于土层100 mm，其内聚力和内摩擦角更大。

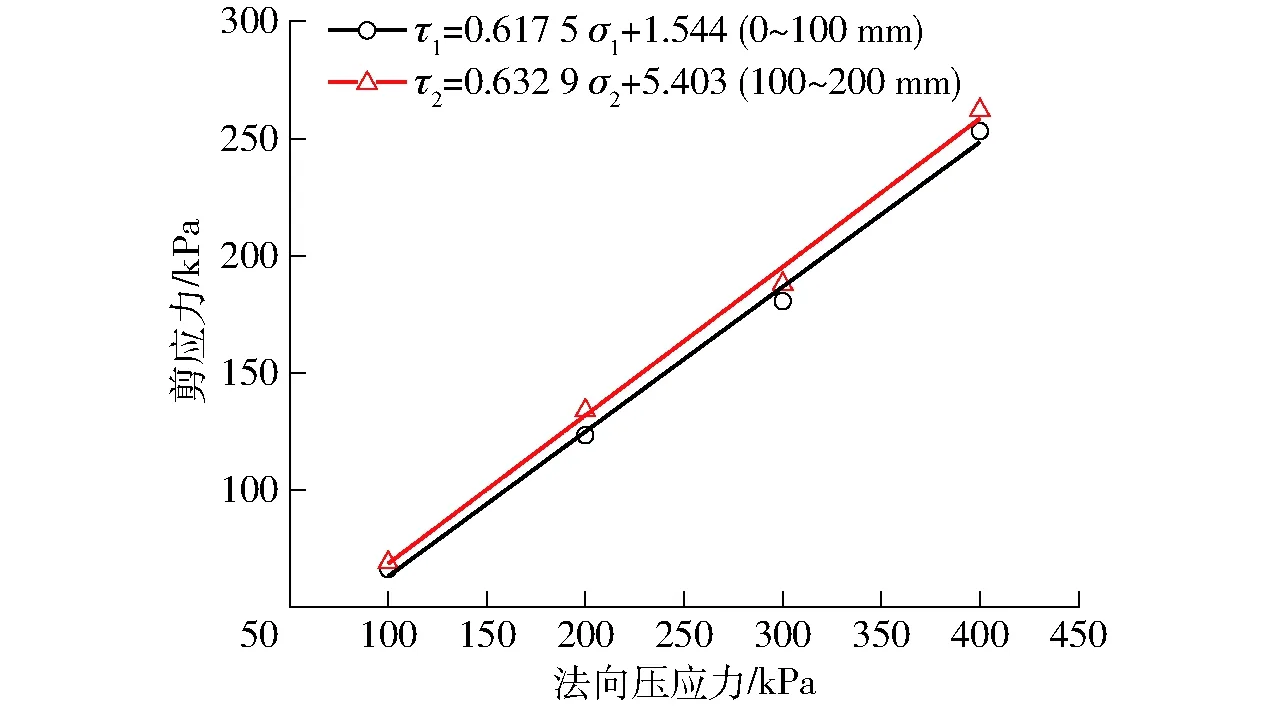
图6 土壤剪应力与法向压应力关系Fig.6 Relationship between shear stress and normal stress

2 土壤接触参数仿真标定

采用试验测试与离散元仿真相结合的方法对桑园土壤进行仿真参数标定及优化，以实测的休止角、滑动摩擦角和抗剪强度为响应值，基于中心组合试验设计(Central composite design,CCD)方案，利用Design-Expert软件分析各因素的编码值和试验数据，利用响应面法建立土壤休止角与试验因素编码值之间的关系；对各项进行方差分析和回归系数显著性检验，分析仿真参数对仿真结果的影响，确定桑园土壤离散元仿真的最优参数。

2.1 土壤仿真离散元模型建立

2.1.1土壤颗粒模型

目前，用于耕作方面的离散元仿真研究，其土壤颗粒尺寸普遍大于土壤真实尺寸[18-20]。综合考虑仿真准确性及计算机计算能力，本文选用非等直径球形颗粒作为土壤颗粒模型，各粒径范围的土壤颗粒质量分数按照实际土壤颗粒质量分数的平均值，根据土壤粒径分级及质量分数，选定仿真所用土壤颗粒直径(取仿真粒径为实际土壤颗粒算术平均粒径的10倍[18])及对应的质量分数如表4所示。

表4 EDEM土壤颗粒直径分布Tab.4 Distribution of soil particle diameter in EDEM

2.1.2接触模型

利用EDEM软件模拟触土部件作业的仿真研究，主要包括土壤颗粒间及土壤颗粒与触土部件间的接触与碰撞，其中，颗粒间的接触模型是仿真分析的基础。EDEM软件内置接触模型主要有：Hertz-Mindlin(no slip)模型、Hertz-Mindlin with Bonding模型、JKR模型、Linear Cohesion模型、Linear Spring模型、Moving Plane模型等。

因不考虑传热及磨损问题，选用Hertz-Mindlin(no slip)模型作为离散元仿真中土壤颗粒与65Mn钢的接触模型[23-24]。此模型由颗粒间的法向力模型及切向力模型共同组成，其中，法向力分量基于 Hertzian接触理论，切向力模型基于Mindlin的研究工作，切向摩擦力遵守库仑摩擦定律，滚动摩擦力由接触独立定向恒转矩模型实现[25-28]。

设两个接触球体颗粒的颗粒半径为Ri、Rj，法向重叠量为δn，则颗粒间接触法向力Fn为

(3)

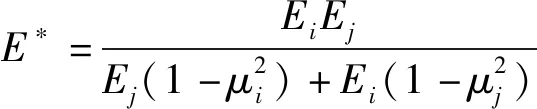
(4)

(5)

式中E*——土壤颗粒的当量杨氏模量，Pa

R*——土壤颗粒的当量半径，m

Ei、Ej——第i、j颗粒的弹性模量，Pa

μi、μj——第i、j颗粒的泊松比

颗粒间的切向力Fτ由切向重叠量δτ和切向刚度Sτ确定，其表达式为

Fτ=-δτSτ

(6)

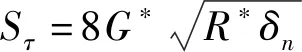
(7)

式中G*——当量剪切模量，Pa

在离散元仿真中，颗粒间的滚动摩擦一般通过在接触表面施加一个力矩来表示，其表达式为

T=-μrFnRiωi

(8)

式中μr——土壤颗粒间的滚动摩擦因数

ωi——颗粒i在接触点处的单位角速度，rad/s

由于土壤颗粒间存在一定的粘聚力，故在仿真时选用Hertz-Mindlin with Bonding模型作为土壤颗粒间的接触模型，该模型通过“粘结键”将两个颗粒粘结在一起，这种粘结作用可以承受一定的法向力和切向力，传递作用力和力矩。两颗粒在设定的粘结时刻之前，其接触模型仍为标准的Hertz-Mindlin(no slip)模型。粘结作用产生后，土壤颗粒的粘结力Fn、Fτ和力矩Mn、Mτ随着时间步从零开始增加。即

(9)

式中A——土壤颗粒间的接触区域面积，m2

Rb——土壤颗粒间的粘结半径，m

J——土壤颗粒的截面极惯性矩，m4

Sn——粘结颗粒法向刚度，N/m

vn、vτ——颗粒运动速度法向、切向分量，m/s

ωn、ωτ——颗粒角速度法向、切向分量，rad/s

Δt——时间步长，s

当外界作用力超过某个预设值时，粘结被破坏。定义法向临界应力σmax和切向临界应力τmax为

(10)

(11)

2.1.3仿真参数

土壤模型参数对仿真结果有重要影响，因此，准确设置土壤模型相关参数尤为重要。所需参数包括材料参数和接触参数。

材料参数主要包括土壤、65Mn钢的密度、泊松比、剪切模量等，此类参数主要通过试验测定及参考相关文献中的参数获得。据相关研究，规则球体的随机填充率为0.56～0.64[29]。桑园土壤颗粒密度采用实测湿密度平均值，仿真中颗粒采用随机生成方式，仿真中土壤颗粒密度为1.79×103kg/m3，土壤和65Mn钢的本征参数如表5所示。土壤颗粒接触半径为1.1倍颗粒半径[30]。

接触参数包括土壤-土壤、土壤-65Mn钢间的静摩擦因数、滚动摩擦因数及恢复系数等。本文利用试验测量与仿真标定相结合的方法获得。根据相关研究[12,23,33-35]，结合仿真预试验，确定土壤-土壤、土壤-65Mn钢间的静摩擦因数、滚动摩擦因数及恢复系数，如表6所示。

表6 离散元模拟接触参数范围Tab.6 DEM simulation contact parameters range

采用EDEM软件进行仿真(计算机CPU为Intel(R) Core(TM) i9-9900KF CPU@3.60 GHz，机带RAM为64 GB，显卡为GeForce RTX 2080Ti，显存11 GB)，通过仿真测定土壤颗粒休止角来确定土壤-土壤间的静摩擦因数、滚动摩擦因数及恢复系数；通过仿真测定土壤与65Mn钢滑动摩擦角来确定土壤-65Mn钢间的静摩擦因数、滚动摩擦因数及恢复系数。设置固定时间步长为Rayleigh时间步长的30%，计算时间步长为0.05 s。

2.2 仿真标定试验

2.2.1土壤颗粒休止角仿真试验

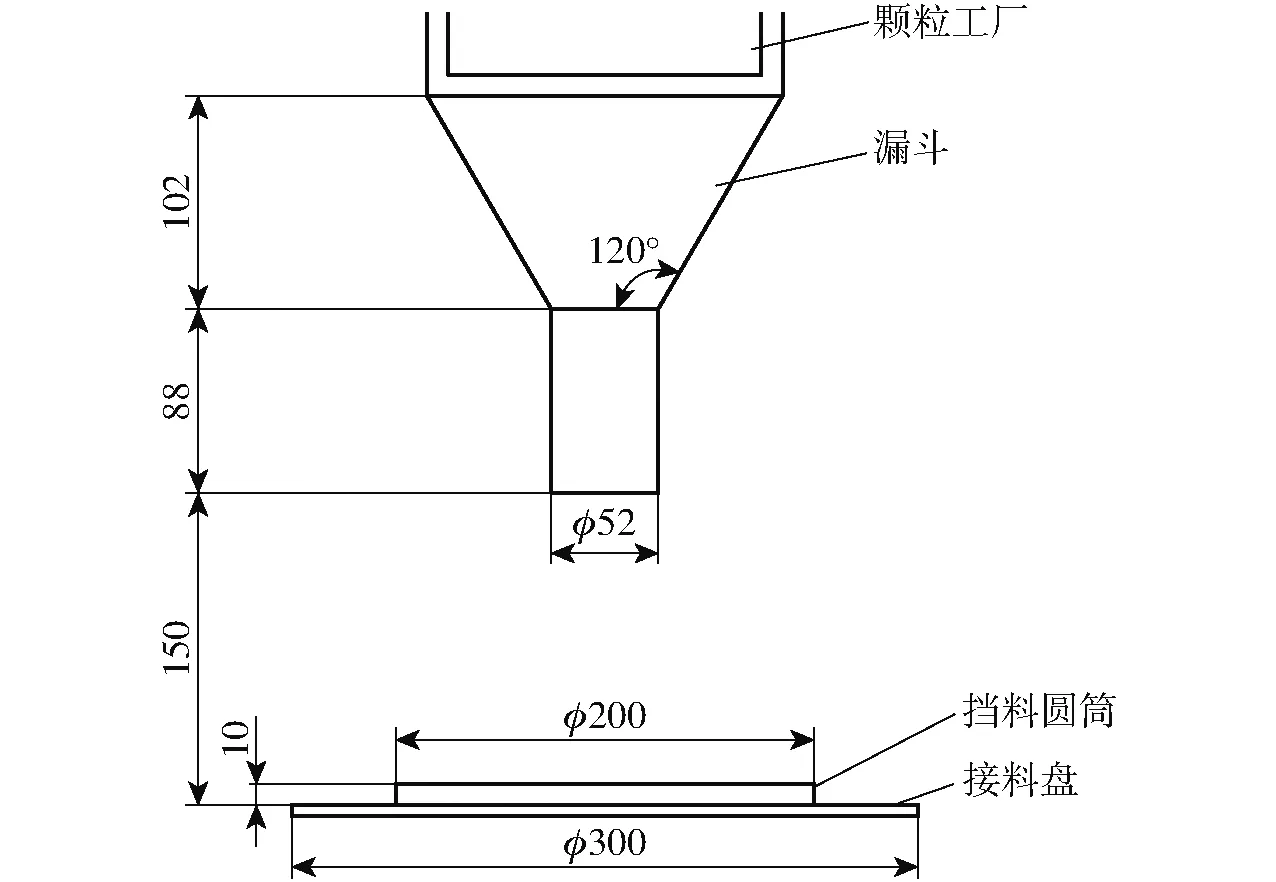
图7 休止角仿真试验仪器尺寸Fig.7 Dimensions of instrument used for simulation test of repose angle

因仿真所用土壤颗粒尺寸大于实际土壤尺寸，结合预仿真试验，确定仿真试验中所使用的漏斗与接料盘的尺寸和相对位置如图7所示。

在进行休止角仿真试验前，还无法确定土壤与65Mn钢之间(土壤-65Mn)的接触参数，故在接料盘上添加φ200 mm×10 mm的挡料圆筒限制底层土壤的水平移动，消除土壤与65Mn间接触参数的影响[18]。仿真时，在漏斗上方设置一φ150 mm×200 mm的圆柱形颗粒工厂，所生成的仿真颗粒直径及其质量分数如表4所示。每组试验以速率1 kg/s生成2 kg仿真颗粒。仿真颗粒经漏斗流出口落向接料盘，待全部颗粒落完并形成稳定的物料堆后结束仿真。并在EDEM中保存其在X轴方向和Z轴方向的正视图，将保存后的正视图导入到Auto CAD中，如图8所示，在水平方向和锥体母线方向分别画一条直线，分别量取角Y1i、Y2i、Y3i、Y4i，计算取其平均值作为休止角Yαi，计算式为

(12)

为探究土壤-土壤间接触参数与土壤休止角的关系，以土壤-土壤间静摩擦因数x1、滚动摩擦因数x2及恢复系数x3为因素，采用中心组合试验设计方法，进行三因素五水平仿真模拟试验，根据表6的参数范围，得到基于中心组合试验因素编码如表7所示。

在土壤休止角仿真试验中，因添加了挡料圆筒，土壤-65Mn钢的接触参数不影响休止角。取表6中各参数范围的中位数，即土壤-65Mn钢间的恢复系数、静摩擦因数、滚动摩擦因数分别为0.35、0.85、0.23进行休止角仿真中心组合试验。所需的土壤-65Mn钢准确参数通过后续的滑动摩擦角仿真试验进行标定。

2.2.2土壤-65Mn钢间滑动摩擦角仿真试验

如图9所示，在土壤-65Mn钢间滑动摩擦角仿真试验中，设置长为500 mm，宽为1 000 mm的矩形倾斜面，在距离倾斜面正上方100 mm处设置长为100 mm，宽为100 mm的长方形颗粒工厂，颗粒工厂下设置100 mm×100 mm×50 mm的无盖无底方盒作为试样盒，每组试验生成0.8 kg颗粒。待颗粒生成完毕，通过给试样盒添加力控制器赋予试样盒一个极小的质量(1×10-5kg，其重力和惯性力可忽略不计)。因EDEM中各部件间无相互作用，方盒可在颗粒的力的作用下随颗粒沿摩擦面移动，即方盒只起到包围颗粒的作用，而不会影响颗粒沿摩擦面滑动。倾斜面以转动速度2(°)/s围绕斜面的定轴转动，直至生成的土壤颗粒在倾斜面上开始滑动，仿真结束[23-24]。在EDEM软件Analyst模块下的Data Browser中读取摩擦面的倾角如图10所示。

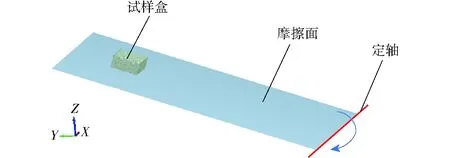
图9 土壤-65Mn钢间滑动摩擦角仿真试验Fig.9 Simulation test of sliding friction angle between soil and 65Mn

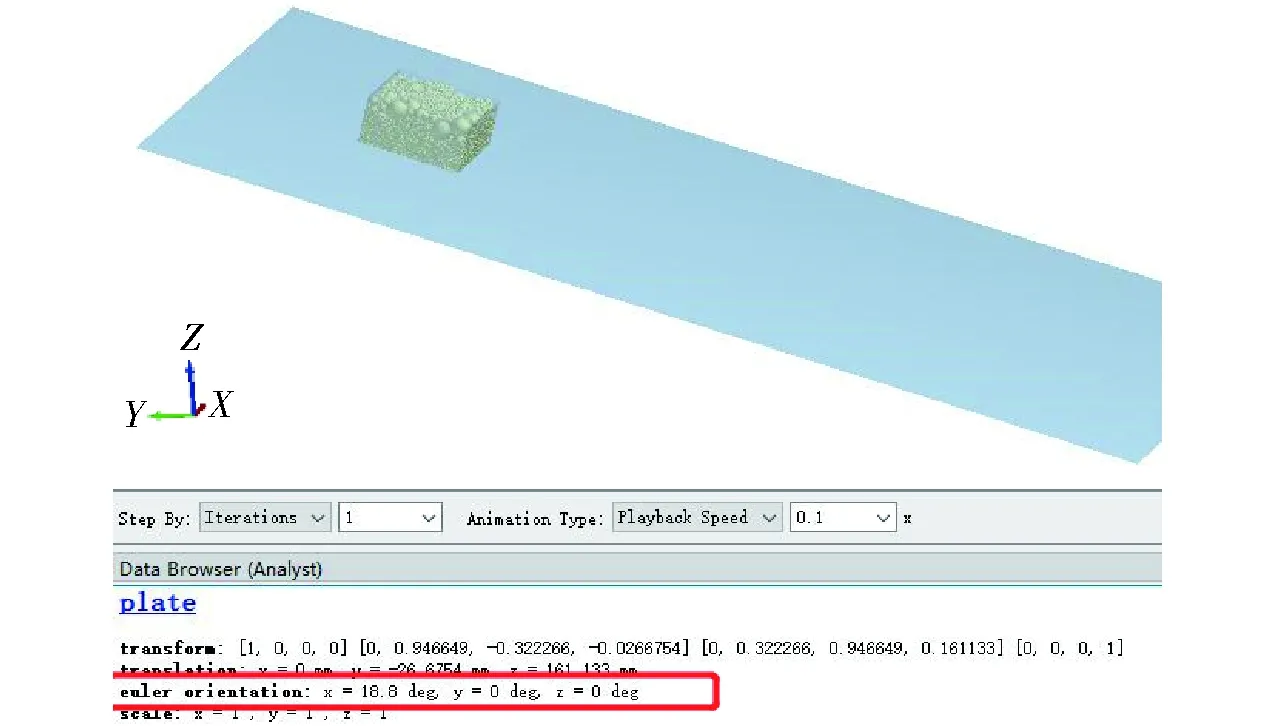
图10 滑动摩擦角的读取Fig.10 Sliding friction angle measurement

为探究土壤-65Mn钢间接触参数与土壤-65Mn钢间滑动摩擦角的关系，以土壤-65Mn钢间静摩擦因数x4、滚动摩擦因数x5及恢复系数x6为因素，采用中心组合试验设计方法，进行三因素五水平仿真模拟试验，基于中心组合试验设计(CCD)编码如表8所示。

2.2.3土壤直剪仿真试验

Hertz-Mindlin with Bonding接触模型中的粘结参数主要包括法向刚度Sn、切向刚度Sτ、临界法向应力σmax、临界切向应力τmax及粘结半径Rb等。此类粘结参数主要通过直剪仿真试验获得。根据已有研究，颗粒行为在此模型下对粘结刚度参数的变化不敏感[10]，取法向粘结刚度为1×108N/m3，取切向粘结刚度为5×107N/m3[36-37]。取σmax=τmax以减少标定参数[31-32]，颗粒接触半径取1.1倍颗粒半径。临界应力是判断粘结键是否断裂的重要指标，其取值与粘结强度密切相关，将直接影响仿真中土壤的破碎程度及作业阻力。以土壤直剪试验土层0～200 mm的内摩擦角结果为标准，校核模型中临界应力的取值。在其他粘结参数确定的情况下，调整临界应力进行土壤直剪仿真模拟试验，得到不同临界应力下的土壤抗剪强度。参照土壤直剪试验的结果进行误差分析，选定合适的临界应力。

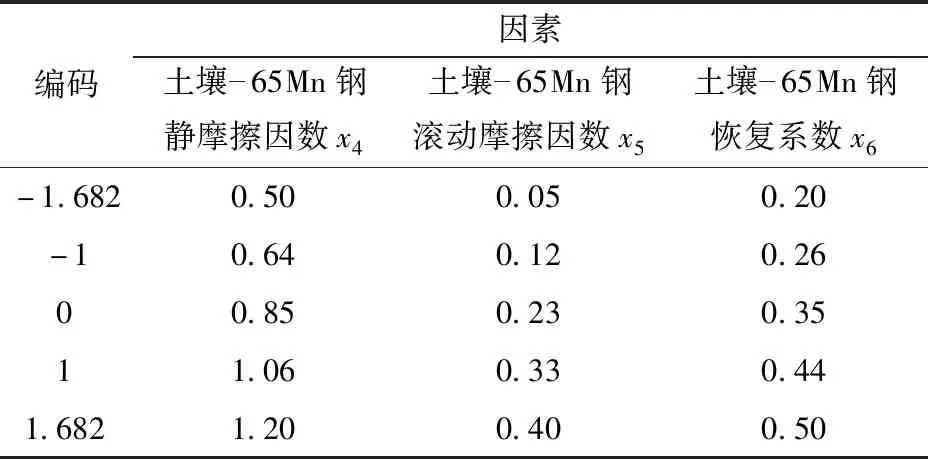
表8 滑动摩擦角仿真试验因素编码Tab.8 Factors and codes of sliding friction angle simulation

根据直剪试验原理，建立仿真模型如图11所示，上、下剪切盒尺寸为φ100 mm×40 mm。下剪切盒上部开口，下部封闭，上剪切盒上下均开口。土壤模型的垂直载荷通过对上剪切盒中的压力板施加垂直向下的移动速度来添加，分析得到土壤颗粒与压力板在垂直方向的接触力即为直剪仿真试验的垂直载荷[10,38-39]。

图11 土壤直剪仿真试验Fig.11 Soil direct shear simulation test

仿真中，下剪切盒以水平速度2 mm/s剪切土壤，当下剪切盒水平位移达到10 mm时，即停止仿真[10,14,38-40]。利用EDEM软件后处理功能，导出仿真过程中下剪切盒所受水平力Fx，根据公式

(13)

计算得到剪应力-位移曲线如图12所示。取其峰值作为土壤剪损时的应力τmax。

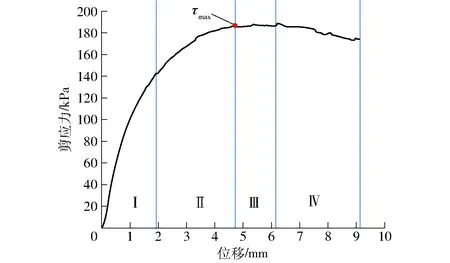
图12 土壤剪应力-位移曲线Fig.12 Shear stress-displacement curve of soil

2.3 仿真试验

2.3.1土壤休止角仿真试验

以各因素编码值X1、X2、X3为自变量，模拟仿真所测得的土壤休止角Yα为目标值，试验设计与结果如表9所示。

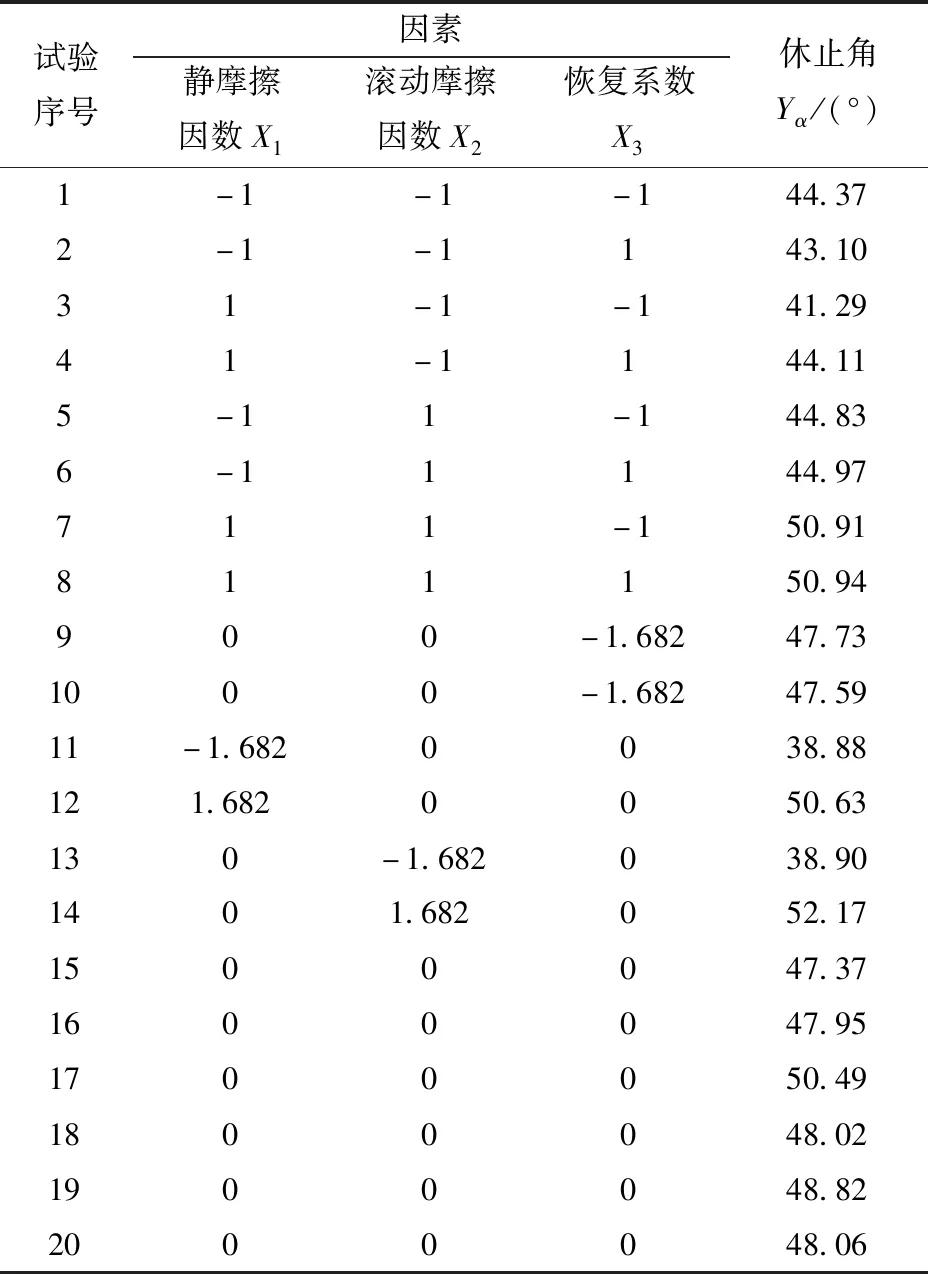
表9 土壤休止角仿真试验设计与结果Tab.9 Simulation test design and result of angle of repose of soil-soil

利用Design-Expert软件分析试验结果，依据表7、9，利用响应面法建立土壤休止角与试验因素编码值之间的关系模型为

(14)

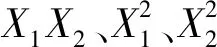
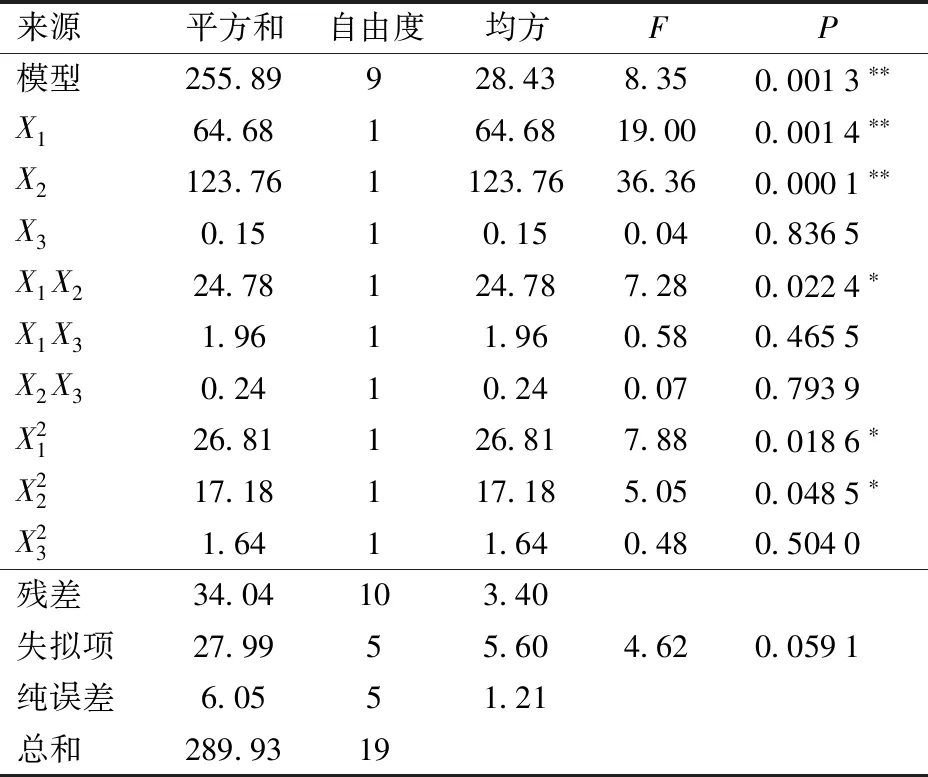
表10 土壤休止角仿真试验响应面方差分析结果Tab.10 Variance analysis of response surface of simulation test of angle of repose of soil

由于本仿真主要研究土层深度0～200 mm内触土部件与土壤的相互作用情况，因此，对土层0～200 mm内土壤休止角进行优化求解。以实际测量的土壤休止角为优化目标，土壤休止角在土层0～100 mm相对于土层100～200 mm仅相差1.52%，因此取两者平均值48.35°作为优化目标，代入式(14)，并进行优化求解，得到若干组优化解，经验证，选取一组最优解为：土壤颗粒间静摩擦因数0.89，土壤颗粒间滚动摩擦因数0.45，土壤颗粒间恢复系数0.43。将得到的最优解作为参数条件进行3次重复仿真试验，得到土壤休止角分别为48.21°、46.83°、47.56°，均值为47.53°，标准偏差为0.69°，与实测休止角48.35°相对误差为1.69%，仿真值与试验值一致。

2.3.2土壤-65Mn钢间滑动摩擦角仿真试验

以各因素编码值X4、X5、X6为自变量，模拟仿真所测得的土壤-65Mn钢间滑动摩擦角Yβ为目标值，试验设计与结果如表11所示。

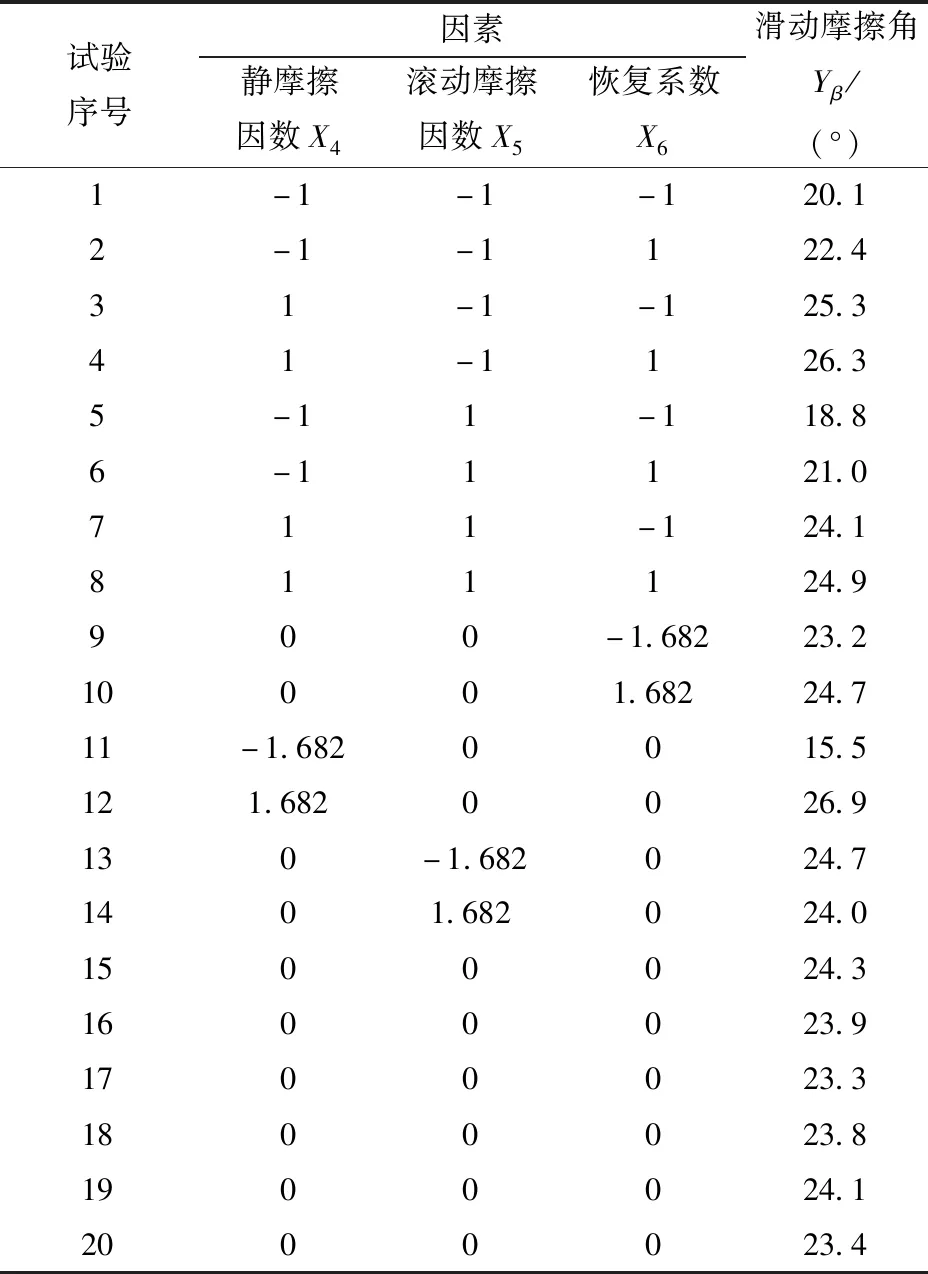
表11 土壤-65Mn钢间滑动摩擦角仿真试验设计与结果Tab.11 Simulation test design and result of sliding friction angle of soil-65Mn

利用Design-Expert软件分析试验结果，依据表8和表11，利用响应面法建立土壤-65Mn钢间滑动摩擦角与试验因素编码值之间的关系模型为

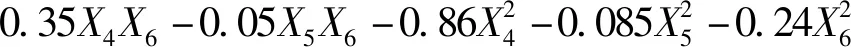
(15)

对土层0～200 mm内土壤-65Mn钢间滑动摩擦角进行优化求解。以实际测量的土壤-65Mn钢间滑动摩擦角为优化目标，土壤-65Mn钢间滑动摩擦角在土层0～100 mm相对于土层100～200 mm仅相差0.22%，因此取两者平均值27.8°作为优化目标，代入式(15)，并进行优化求解，得到若干组优化解，选取一组最优解为：土壤-65Mn钢间静摩擦因数1.15，土壤-65Mn钢间滚动摩擦因数0.05，土壤-65Mn钢间恢复系数0.4。将得到的最优解作为参数条件进行3次重复仿真试验，得到土壤-65Mn钢间滑动摩擦角分别为28.1°、27.5°、29.3°，均值为28.6°，标准偏差为0.61°，与实测滑动摩擦角27.8°相对误差为2.88%。

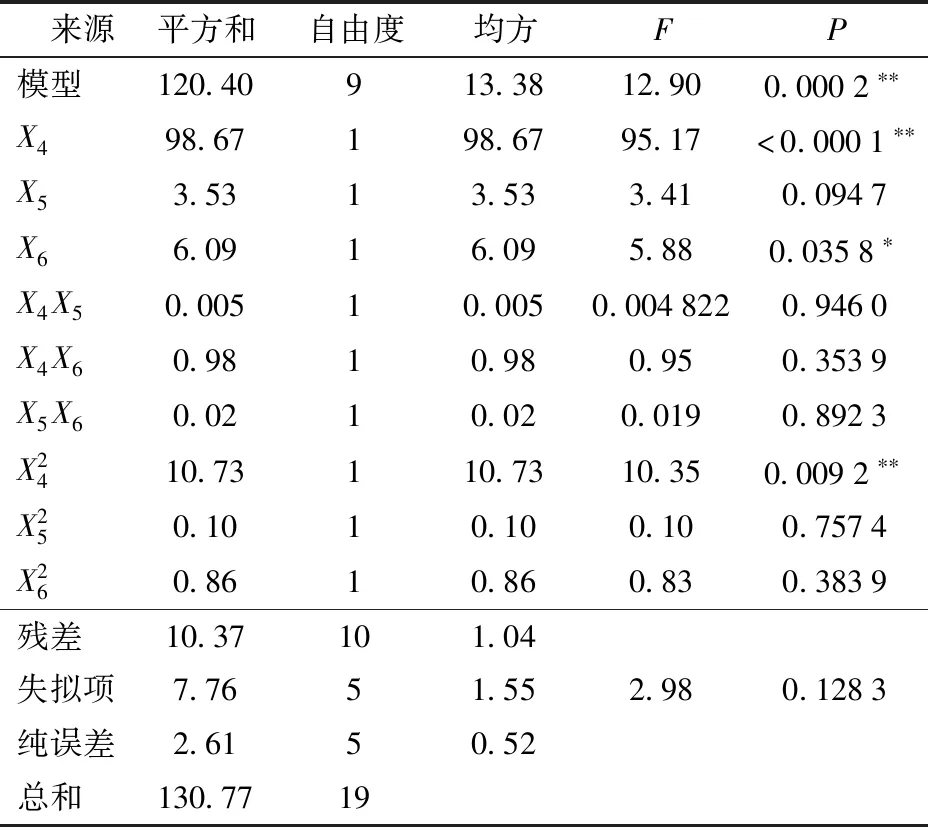
表12 土壤-65Mn钢间滑动摩擦角仿真试验响应面方差分析Tab.12 Variance analysis of response surface of simulation test of sliding friction angle of soil-65Mn

2.3.3土壤直剪仿真试验

选择土壤直剪试验土层100、200 mm的内摩擦角试验结果的平均值32.01°为标准，经反复试验，当临界正应力和临界切应力均为10 kPa时，得到内摩擦角仿真值为30.24°，仿真值与试验值相对误差为5.53%，故最终确定接触模型中的临界应力为10 kPa。剪切试验中，从剪切盒外部沿着垂直于正压力方向和剪切位移的方向观察，粘结键分布及其受力云图如图13所示。

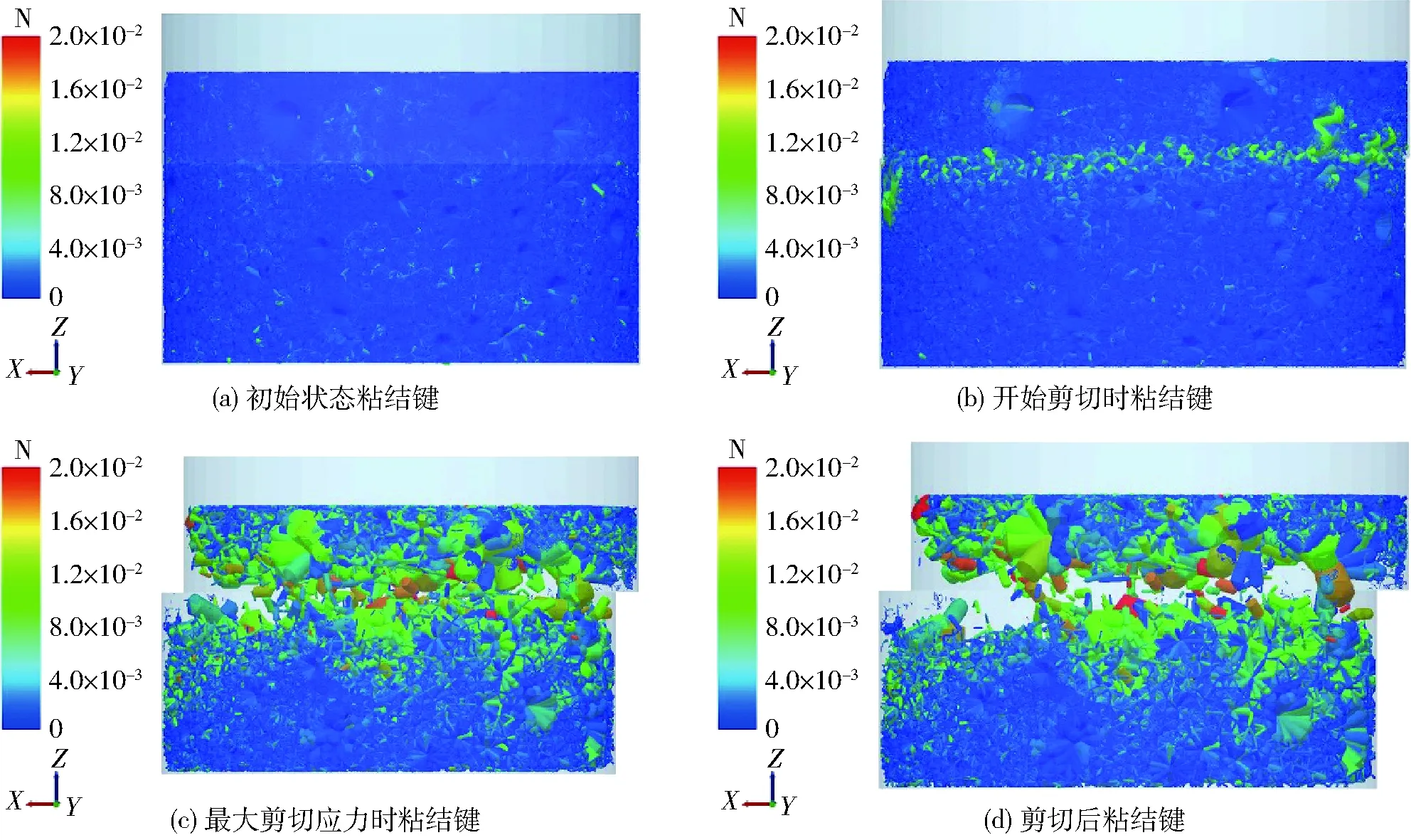
图13 剪切仿真过程中粘结键及其受力云图Fig.13 Bond and its force nephograms in shear simulation

图13a为初始状态的粘结键，此时由于压板垂直向下的压力，颗粒间的粘结键受到较小的力，各处受力均匀。图13b为下剪切盒开始移动，但土壤样本未发生剪切破坏时粘结键的受力情况，由图可知，剪切面处的粘结键受力较大，由于剪切力未超过粘结键的断裂强度，粘结键未发生断裂，试样整体呈现弹性体特征，对应图12中的Ⅰ段，此时剪切应力与剪切盒位移成线性关系；图13c为剪切应力达到最大时的粘结键受力和断裂情况，此时剪切面附近的粘结键几乎全部断裂，对应图12的τmax点，即剪切应力达到最大值。在达到最大剪切应力前，因部分颗粒间的挤压、摩擦力增大，部分粘结键超过断裂强度而发生断裂，颗粒间产生相对运动，导致土壤样本局部发生剪切破坏，因此图12中达到最大剪切应力前(Ⅱ段)，位移-剪应力曲线出现明显的非线性段。达到最大剪切应力后，剪切面处土壤颗粒间的粘结键已断裂殆尽，颗粒间的粘结力急剧减小，土壤试样整体所受到的剪切应力主要受颗粒间的摩擦和挤压力影响，因此剪切应力趋于平稳，对应图12中的Ⅲ段。在下剪切盒不断移动的同时，剪切面随剪切盒不断移动而缩小，导致相互接触的颗粒数量减少，颗粒间的摩擦和挤压也随之减少，剪应力在达到最大后有所下降，对应图12中的Ⅳ段。在到达最大剪切应力后，仍有部分粘结键因颗粒间的挤压或摩擦而断裂，如图13d所示。

综上可知，剪切仿真试验所标定的参数及仿真过程能反映真实的剪切试验过程，模型和接触参数标定合理。标定的桑园土壤离散元仿真参数如表13所示。

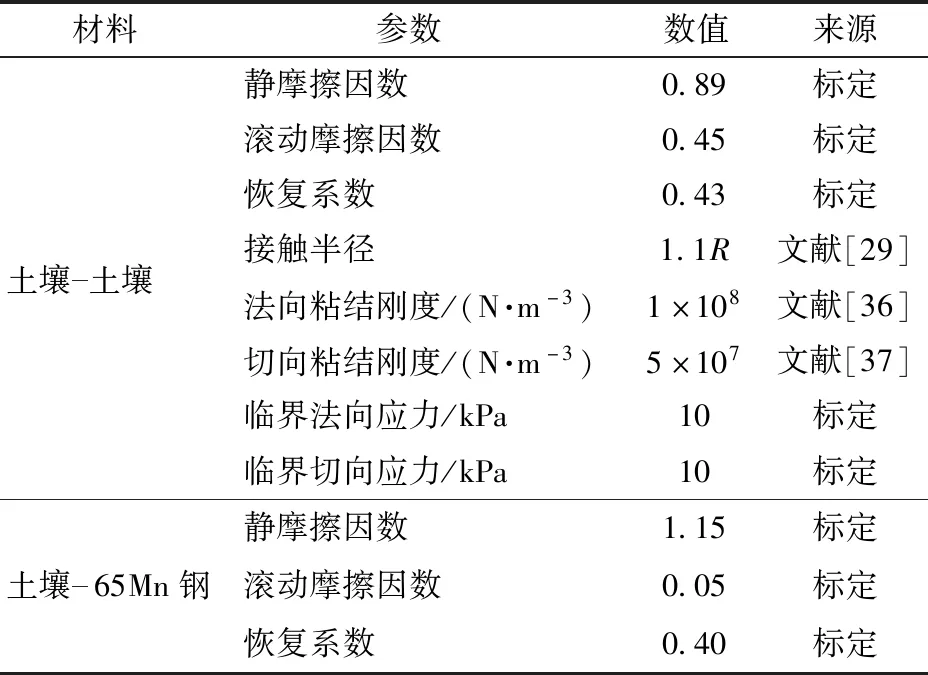
表13 桑园土壤离散元仿真参数Tab.13 Discrete element simulation parameters of soil in mulberry field

3 结论

(1)通过对土壤休止角仿真试验，标定土壤-土壤间静摩擦因数、滚动摩擦因数、恢复系数分别为0.89、0.45、0.43，仿真验证试验得到休止角为47.53°±0.69°，仿真值与试验值相对误差为1.69%。

(2)通过土壤-65Mn钢滑动摩擦角仿真试验，标定土壤-65Mn钢间的静摩擦因数、滚动摩擦因数和恢复系数分别为1.15、0.05、0.4，仿真验证试验得到滑动摩擦角为28.6°±0.61°，仿真值与试验值相对误差为2.88%。

(3)通过土壤直剪试验仿真，标定Hertz-Mindlin with Bonding接触模型中土壤-土壤颗粒的法向粘结刚度和切向粘结刚度分别为1×108N/m3和5×107N/m3，接触半径为1.1倍颗粒半径，临界法向应力为10 kPa、临界切向应力为10 kPa时，仿真得到内摩擦角为30.24°，仿真值与试验值相对误差为5.53%。

(4)提出了桑园土壤离散元仿真物理参数系统标定的方法，建立了桑园土壤的非等直径土壤颗粒离散元仿真模型，通过对试验测得和仿真所得的休止角、滑动摩擦角及土壤内摩擦角分析与比较可知，试验值与仿真预测值一致。可以用本文提出的标定方法及其参数值，进行桑园耕作机械触土部件与土壤相互作用的离散元仿真分析及其结构优化。