基于三维点云的运输车粮箱动态均匀装载方法研究

王枭雄 王 卓 白晓平 葛志康 赵泳嘉

(1.中国科学院沈阳自动化研究所，沈阳 110016；2.中国科学院大学计算机科学与技术学院，北京 100049；3.中国科学院机器人与智能制造创新研究院，沈阳 110169)

0 引言

随着自动驾驶技术的发展，特别是主从式协同控制技术的发展，联合收获机-运输车协同控制的自动收获作业方式被广泛研究与应用[1-4]。其作物卸料装车普遍采用固定装载点，或预设装载路径的方式进行，在无人工参与平仓的情况下，其装载率较低。有效的装载方法对于提高运输车粮箱装载率，进而提高主从协同作业的效率具有重要意义。

为了在装载过程中建立有效的数据反馈，需要对运输车粮箱的装载状态进行检测。目前对粮箱装载状态的识别主要有基于超声波传感器[5]、基于压力传感器[6]和基于机器视觉[7-9]的方法。在沥青混凝土卸料装车系统中，王芳等[5]使用超声波传感器来检测料堆的高度，田明锐等[8]使用机器视觉的方法，通过测量料堆角度和高度信息，来判断运输车箱的装载情况。王录民等[6]通过在粮堆底部安装压力传感器，利用粮堆高度与底部压力的近似线性关系判断谷物分布状态，完成对静态下的粮仓装载状态测量。陈莹等[7]使用CCD相机从多个角度拍摄堆料的侧视图，通过各个横截面的面积来计算大型堆料的体积。LIU等[9]使用基于机器视觉的方法，利用谷物与粮箱的接触线来检测装载状态，将粮仓划分为4个区域，通过设定阈值来判断其装载状态。

目前，由于对装载状态检测的精度不高，基于此进行的装载方法对装载率的提高有限。近年来，基于三维点云的测量与目标重建被广泛研究，通过双目视觉[10]、结构光[11]或激光雷达[12-13]来完成对目标的测量，在果树测量[14-15]和动物体尺测量[16-17]等农业领域取得了良好的效果。

本文提出基于三维点云的联合收获机-运输车卸料装载方法。该方法运用多个相机获取能准确反映运输车粮箱装载状态的三维点云，以此进行装载均匀性评估，通过实时调整卸料装载点位置，使粮箱始终保持在均匀的装载状态，从而提高满载时的粮箱装载利用率，同时提高装载过程中运输车粮箱的稳定性，降低溢料的可能性。针对装载物相互遮挡造成的点云不完整问题，建立堆体的物理模型和相机遮挡模型，来估计盲区点云高度，从而进行点云填充，以得到完整的装载状态信息。

1 检测装置与方法

1.1 检测装置

通常运输车粮箱为上方开口的长方体结构，如图1所示。为了避免对联合收获机-运输车协同作业过程中的卸料装载过程造成影响，且相机安装在超出车体宽度的区域时存在安全隐患，相机的可选安装区域被限定在粮箱四周的上方区域，如图1中的阴影部分。考虑到安装过高时，相机与粮箱难以进行刚性连接，车辆行驶过程中的振动会对相机的检测造成影响，安装高度通常受到限制。

图1 相机安装位置与粮仓示意图Fig.1 Camera installation location and granary diagram

由于单个相机的可视范围难以覆盖较大的粮箱，而增加相机数量会增加成本，同时提高系统的复杂度，本文使用2个相机，通过调整相机的安装位置及相机视场的俯仰角、偏航角和滚动角来提高相机视场对粮箱区域的覆盖率[18]。

相机的三维有向感知模型如图2所示，其由P、λ、θ、ω、2α、2β、d等7个因素确定[18]，其中P为相机的安装位置坐标(x,y,z)，如图1所示，其取值范围为

(1)

式中a、b、c——粮箱的长度、宽度和高度

h——相机安装的限制高度

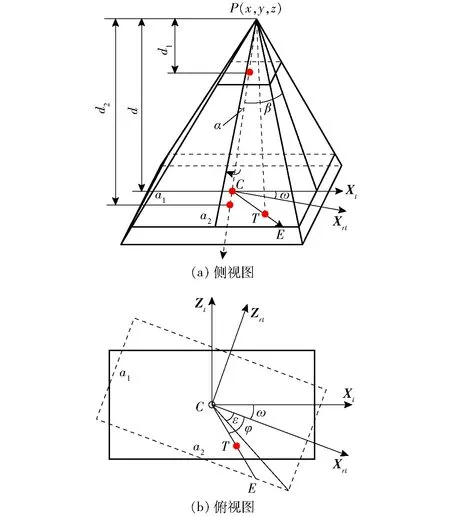
图2 相机三维有向感知模型Fig.2 3D directional sensing model for camera

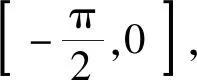
(2)

ω为相机绕光轴PC的滚动角(右手定则)，取值范围为[0,π]，2α、2β分别为相机水平方向视场角和垂直方向视场角，d为相机的最佳成像距离，取值范围为[d1,d2],d1、d2为相机的最近成像距离与最远成像距离。

为了准确地对粮箱的装载状态进行检测，相机的视野范围应尽可能多地覆盖粮箱内装载物堆体的表面，而作物在粮仓内的装载包括从空载到满载的多种情况，将堆体表面在粮箱内的分布近似简化为均匀随机分布，则相机对堆体表面的覆盖率可由相机对粮仓空间的覆盖率进行度量。将粮箱空间离散化为等距离的离散点，对于满足上述条件的任意一个相机安装位姿(x0,y0,z0,λ0,θ0,ω0)，依据空间点覆盖判定准则计算覆盖率η[18]，计算式为

η=|ψa|/|ψ|

(3)

式中 |·|——求集合中元素总数的运算符号

ψ——空间区域的空间点集合

ψa——相机视场覆盖的空间点集合

对于粮仓离散空间中的任意一点T(x0,y0,z0),如图2所示，在相机安装位置为P(x,y,z)时，其属于相机视场覆盖的空间点集合ψa的条件为

(4)

其中

(5)

(6)

式中ec——相机感知方向单位矢量

Xt——相机的视场滚动角为0°时，相机水平视场方向单位矢量

Xrt——相机的视场滚动角为ω时，相机水平视场方向单位矢量

Zt——相机的视场滚动角为0°时，相机垂直视场方向单位矢量

lPT、lPC、lCT、lCE——两点间的长度向量

据此可以得到使用任一安装参数时的相机视场覆盖率，然后使用视场覆盖增强算法进行优化，得到覆盖率最大的相机安装参数[18]。

当其中一个相机的安装位置和姿态确定后，另一相机采用与其几何对称式的安装位姿，即若相机1的安装位姿为(x1,y1,z1,λ1,θ1,ω1)时，相机2的安装位姿为(x2,y2,z2,λ2,θ2,ω2),计算式为

(7)

采用这种对称式的安装方式，能避免堆体由于自身遮挡而使相机无法观测到堆体全貌的情况。

1.2 点云数据预处理

为了将2个相机获取的点云数据进行融合，采用张正友标定法[19]对各个相机进行内外参数的标定。由于2个相机有重叠视野，制作标定图像时，保持标定板位置Cb不变，由2个相机分别采集图像p1、p2加入到标定集P1、P2中，则可得到2个相机相对于标定板位置Cb的外参矩阵H1、H2。

利用矩阵H1、H2对点云数据进行坐标变换，则将2个点云数据统一到标定板Cb的坐标下，再使用迭代最近点(ICP)算法[20-21]进行精配准，使其融合为一个点云，经过简单的平移或旋转变化则可得到世界坐标系XOY下的点云数据。

1.3 点云填充

由于装载物之间相互遮挡，融合后的点云存在孔洞，不能完整地表达粮箱的装载状态，也不利于后续处理，所以需要进行点云填充。国内外学者针对点云填充进行了许多研究，何东健等[22]使用改进的三次B样条曲线对奶牛点云的缺失区域进行修复，NOWAK等[23]提出了一种基于贝塞尔曲面的空腔重建方法用于三维扫描的人体表面填充，GAI等[24]使用径向基函数来恢复复杂表面孔洞的信息。这些方法在点云填充上取得了良好的效果，但是其仅根据孔洞临近点进行填充，未充分利用盲区的形成条件，在堆体遮挡所形成的盲区进行填充时误差较大。为此，本文建立盲区模型进行点云填充。

单一颗粒材料在连续浇筑过程中形成的堆体可以由安息角进行表征[25-26]，形成的堆体可以近似为圆锥。图3为堆体与相机视野的遮挡示意图，其中△ABC为崩塌后的圆锥形堆体的横截面，δ0为堆体ABC的安息角，相机安装在堆体右上方，由于堆体ABC对相机视野的遮挡，在OE段形成盲区。依据堆体的物理模型，堆体的安息角不变，堆体的高度AE与其底面半径BE呈线性关系。为了使可观测到的堆体表面的截面AC稳定存在，盲区OAE内堆体的最小分布状态为以点A为顶点的截面为△ABE的半圆锥，即在盲区截面AOE内，ABE部分的装载状态确定，仅在OAB区域内的装载状态不确定。如图3a所示，当向盲区OE内进行装载时，可形成高度不超过视线OA的各种堆体，所以盲区OAB的装载状态存在空载到满载的各种可能的装载状态。为使估计的点云分布与实际的点云分布的期望误差最小，取盲区内点云可能分布的最大高度与最小高度的平均值作为该点的估计高度，如图3b所示，OFA即为估计的盲区OE内的点云分布的截面。其中δ1与δ2均小于安息角δ0，即OFA是可能形成的稳定堆体表面。

图3 堆体与盲区示意图Fig.3 Schematics of heap and its blind area

当2个堆体相互遮挡时可能形成的截面如图4所示，分别为两谷堆A1B1C1与A2B2C2之间相互重叠，以及相互不重叠2种状态。O1、O2为盲区的边界点，绿色阴影区域为确定的装载状态，黄色阴影区域为可能的最大装载状态。同样取某点可能的最低装载高度hmin与该点可能的最高装载高度hmax的平均值为该点的估计装载高度h，即

(8)

图4 堆体相互遮挡形成的盲区示意图Fig.4 Schematics of two heap and its blind area

将点云集合Ω⊂R3投影到XOY平面，得到二维点集Ω′⊂R2，盲区的俯视图如图5所示。对于盲区内一点Q(x,y,z)，其在XOY平面内的投影为Q′(x,y)。C′1、C′2分别为两相机的安装位置C1、C2在平面XOY上的投影。连接C′1与Q′并延长，其与盲区边界相交于O′11与O′12两点；同样连接C′2与Q′并延长，其与盲区投影的边界相交于O′21与O′22两点。O′11、O′12、O′21、O′22分别为点云集合Ω内的点O11、O12、O21、O22在XOY平面内的投影。以O11、O12、O21、O22这4个点为顶点，形成的圆锥堆体底面的半径为dij，计算式为

(9)

式中zij——点Oij的z坐标δ——堆体安息角

当点Q在以点Oij为顶点的圆锥上方时，点Q的最低高度hmin受到点Oij所在堆体的影响，否则不受其影响。定义点Q的最小高度hij为

(10)

式中d′ij——Q′与O′ij的距离

则点Q(x,y,z)的z坐标最小值为

hmin=max{hij|i,j=1,2}

(11)

点Q的最大高度hmax受到所有通过点Q′正上方的相机视线的影响，即所有在XOY平面上的投影通过点Q′的相机视线。由于所有的相机视线都通过相机安装位置点C1或点C2，即所有相机视线在XOY平面上的投影都通过点C′1或点C′2。所以通过点Q′的相机视线投影仅有直线C1Q′和C2Q′。

定义相机视线通过点Q′正上方时的视线高度gi为

(12)

式中d(C′i,Q′)——点C′i与点Q′的距离

d(C′i,O′i1)——点C′i与点O′i1的距离

Ci,z——点Ci的z坐标

Oi1,z——点Oi1的z坐标

则点Q(x,y,z)的z坐标最大值为

hmax=min{g1,g2}

(13)

点Q(x,y,z)的z坐标z=h可由式(8)～(13)得到。由此，对盲区投影内的任意一点Q′(x,y)，可估计其空间坐标Q(x,y,z),完成点云填充。

1.4 装载方法

1.4.1装载均匀性评估

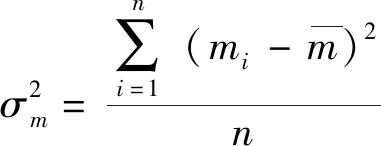
(14)

进一步方差可表示为

(15)

其中

(16)

ρ——装载物密度

即装载均匀性可由装载面积s上的平均高度h的方差进行评估。

1.4.2装载点位置计算

(17)

装载后整体的方差计算式为

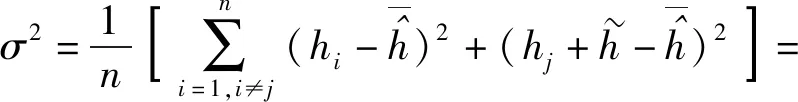
(18)

其中1≤j≤n，最均匀装载网格l=argminσ2(j)，此时l=argmin{hi,1≤i≤n}。

利用离散化后的网格平均高度的方差进行均匀性评估时，每次选取当前平均高度最低的网格进行装载，只考虑了各个网格的装载量在数值上无序化后的均匀性，未能充分考虑不同装载量在位置上的相互关系。当粮箱内存在多个相同的最低平均高度的网格时，装载点位置的选择具有一定的随机性，然而此时不同装载点位置的选择所产生的装载均匀性效果不同。如在粮箱空载时，固定选取离粮箱几何中心最近的网格进行装载，而在其后进行的装载过程中，亦存在多个相同的最低平均高度的网格的情况，若装载点全部连续地选取在粮箱的一侧(图6a)，其整体装载均匀性较差，粮箱右侧装载量明显高于左侧，装载物的重心偏向粮箱几何中心的右侧。在相同装载量的情况下，图6b为更加理想的装载状态，其整体装载均匀性较图6a更好，装载物的重心与粮箱的几何中心重合，在均匀装载的同时，可以降低由于装载后车辆重心偏移对车辆行驶的稳定性的影响。为此，引入重心偏移量进行辅助评估，使装载物整体的重心尽可能地靠近粮仓的几何中心。

装载物的重心坐标(xc,yc)计算式为

(19)

(20)

式中mc——当前装载物的质量

则重心偏移量d为装载物重心与粮仓几何中心的距离，计算式为

(21)

式中 (xk,yk)——粮仓几何中心点坐标

通常最均匀装载点与最小重心偏移量的装载点不同，甚至会出现向一个网格装载后，装载均匀性提高(方差减小)，而重心偏移量也增大的情况。为此设计一个选择策略在二者之间进行权衡。

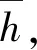
装载点的选择策略如下：将粮箱离散化，选取平均高度最小的网格的中心作为装载点,则该装载点为最均匀装载点。当存在多个相同的最小平均高度的网格时，计算向这些网格装载后的装载物重心偏移量，选取其中重心偏移量最小的网格作为装载点。

1.4.3可行性与鲁棒性分析

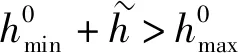
(22)

(23)

(24)

其中

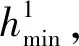
(25)

则有

(26)

从而有

(27)

(28)

(29)

即此后每个装载周期选取平均高度最低的网格进行装载后，该网格的平均高度成为当前所有网格中的最大值，则在n个装载周期后，所有网格都进行且仅进行了一个装载周期的装载过程，装载状态由GK变为

(30)

由此可得

σ(GK+t)=σ(GK+t+n) (t∈N)

(31)

即装载呈现周期性变化，平均高度的方差也呈现周期性变化，周期为n。由于方差可取的值为有限个，所以装载状态的方差σ(GK+t)存在最大值σmax。

假设t0个装载周期后方差达最大值σmax，则有

σmax=σ(Gt0)

(32)

将式(17)代入式(18)可得

(33)

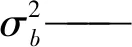
由于σ(Gt0)>σ(Gt0-1)，代入式(33)得

(34)

(35)

由于σ(Gt0)>σ(Gt0+1)，代入式(33)得

(36)

(37)

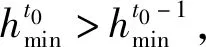
(38)

将式(17)代入式(38)有

(39)

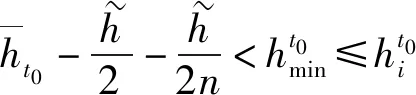
(40)

将式(29)代入式(37)有

(41)

联立式(40)、(41)有

(42)

则

(43)

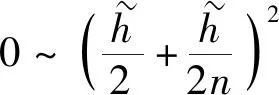
该方法对不同的初始装载状态具有很强的鲁棒性，装载过程中，由于突发的颠簸或者其他意外情况导致未能在指定的位置进行装载时，此后的装载过程可将当前期望之外的装载状态视为初始状态继续进行装载，亦能达到既定的装载状态，即该方法具有抗干扰性。

2 实验与结果分析

2.1 实验装置

为了验证装载方法的有效性，搭建如图7所示的实验平台进行实验验证。实验粮箱为2.0 m×2.0 m×0.65 m的长方体，由于安装工具自身高度的影响，相机的最低安装高度限制为0.8 m，最高安装高度限制为1 m。获取装载状态的三维点云所使用的相机型号为MYNT-D1000-IR-120/Color,其帧率为60 f/s,深度分辨率为1 280像素×640像素，工作距离为0.32～7 m，水平方向视角为105°，垂直方向视角为58°。

图7 实验平台Fig.7 Experiment platform

为了确定相机的安装参数(x,y,z,λ,θ,ω)，采用Matlab的遗传工具箱进行6参数优化，其取值范围的下限为{0 m,0 m,0.8 m,-π/2,0 rad,0 rad}，取值范围的上限为{0 m,2 m,1 m,0,π,π}。适应度函数取相机视场对粮箱空间的覆盖率，其中粮仓空间离散为间距为5 cm的点集。Matlab中除参数初始值设定为与参数的取值范围一致外，其他保持默认设置。经过遗传算法优化后得到的其中一个相机的安装参数为(0 m,0 m,0.8 m,-0.53 rad,0.785 rad,0 rad),由式(7)可以计算得到另外一个对称安装的相机的安装参数为(2 m,2 m,0.8 m,-0.53 rad,3.925 rad,0 rad)。为了对点云进行对比，配置了参考相机来获取盲区的点云状态作为实际点云分布，与算法填充的点云进行对比。3个相机均通过相机云台进行固定，便于进行安装角度的调节。

目前已有稻谷、马铃薯、玉米、甘蔗、甜菜等农作物使用特定的收获机进行收获作业，本文选取2020年产自徐州市的冬季甜菜作为装载对象。与氧化铝等金属粉末安息角的测量[27]不同，农作物安息角的测量没有相关的标准。孙骊等[28]对小麦和玉米等种子的安息角进行了初步研究，发现依照安息角的变化规律，可以预测某类种子在一定条件下的安息角。为了得到甜菜在装载过程中的安息角，使用与装载过程中相同大小和含水率的甜菜进行安息角的测量，并使用相同的跌落高度与相同质地的地面，通过多次测量，取其平均值33.80°作为甜菜的安息角。

将装载状态检测与动态均匀装载方法搭载在车载平台Jetson AGX Xavier上运行，使用C/C++作为实现语言，将上述Matlab离线处理得到的坐标转换矩阵，以及实验得到的安息角等参数写入算法中直接使用，这些参数一经获取，在后续的实时检测与动态均匀装载算法中不再变动，无需重复计算。在实时检测的三维重建上，一方面通过体素下采样、条件滤波等方法在不丢失关键数据的情况下大幅降低三维点云的数据量，另一方面充分利用Jetson的GPU资源，使用C/C++与CUDA混合编程，将包括体素下采样、条件滤波等方法在内的三维建模与装载方法并行化，以满足联合收获机-运输车协同作业的实时性要求。

2.2 实验结果

2.2.1点云填充实验结果

图8为粮箱在轻载、中载和重载3种不同装载状态下甜菜的三维点云，其中左图为2个实验相机获取的甜菜装载状态的三维点云，中间为依据本文提出的算法进行点云填充后甜菜的三维点云，右图为2个实验相机和参考相机获取融合后的甜菜的三维点云。

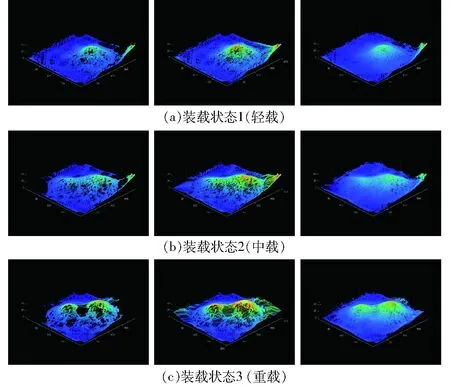
图8 不同装载状态下的三维点云图Fig.8 Three-dimensional point clouds under different loading states

可以看到，不同装载状态下，采用2个实验相机获取的甜菜装载状态的三维点云均有不同程度的空缺，且装载不均匀程度增加时，甜菜之间的相互遮挡情况加剧，导致盲区变大。与2个实验相机获取的原始三维点云(左)相比，经过点云填充处理后的三维点云(中)，能更加完整地反映甜菜的装载状态，没有大片的不确定区域;经过点云填充处理后的三维点云(中)与加入参考相机后获取的三维点云(右)相比，两者的三维点云所反映的装载状态的一致性较好。

3种状态下进行点云填充的平均误差分别为4.62、0.17、0.21 cm。装载状态1的盲区主要分布在靠近其中一个相机的位置，且附近有较高的堆体对另一相机形成了遮挡，导致其依据相机遮挡模型得到的最大高度较高，而其实际状态分布为最小状态，所以在该处盲区的点云高度估计的误差相较于装载状态2和装载状态3的误差较大。3种装载状态下的点云填充误差均低于5 cm。

填充后的三维点云(中)的稠密度较实际的三维点云(右)稀疏，一方面由于在对左侧点云进行填充时，对于较小的盲区，由于其对装载状态的影响较小，未进行点云填充；另一方面在对盲区进行填充时，只保证能完整表达该区域的装载状态，未进行高密度填充，这样能加快点云的填充速度。

2.2.2装载方法仿真结果

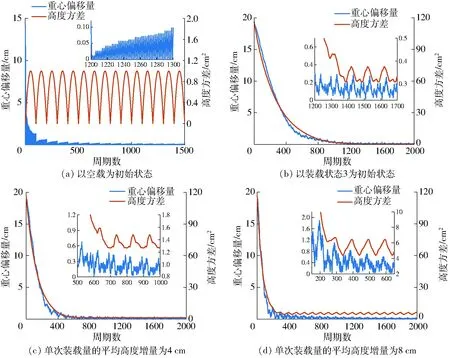
图9 装载过程中高度方差与重心偏移量变化曲线Fig.9 Variance of height and offset of center of gravity during loading

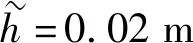
为了验证装载方法的鲁棒性，选取实验中采集的装载状态3为初始装载状态，进行仿真，其重心偏移量和高度方差的变化如图9b所示。可以看到初始的装载不均匀性和重心偏移量都较大,随着装载过程的继续，高度方差和重心偏移量迅速减小，在装载周期数达到1 400时装载不均匀性达到最小值，如图9b中局部放大图所示，随后进入稳定状态，此后装载均匀性(高度方差)呈周期变化，其方差最大值亦满足式(43)。进入稳定状态后，重心偏移量亦开始周期变化，但其幅值周期性的不断减小，在装载过程持续时，无限趋近于0。

相较于从空载状态开始的装载过程(图9a)，装载过程进入稳定状态后，从装载状态3开始的装载过程(图9b)，在稳定状态下，其最小重心偏移量较高，且最小高度方差也相对较大。这是由于最小装载量的存在，装载方法无法在任意的装载状态下，将粮仓的装载状态变为最均匀状态(高度方差和重心偏移量均为0)。

最小装载量受到装载物颗粒大小和最小装载速度的影响，在一个具体的装载过程中，装载设备和装载物已经确定，即最小装载量固定，可以通过增加装载速度和提高装载周期来增加单周期装载量。一个连续的装载过程可以离散为以装载周期为间隔的一次次的装载，为了研究单次装载量对装载过程的影响，分别选取单次装载量的平均高度增量4 cm和8 cm进行仿真，结果如图9c、9d所示。

可以看到，由于单次装载量的增加，装载过程在更短的装载周期内达到稳定状态。单次装载量越大，其在稳定状态下的装载不均匀性越大，重心偏移量在一个稳定周期内的波动范围也越大。但当单次装载量增加时，装载相同质量的装载物，所需装载周期更短，这也意味着装载位置的变化次数降低。实际应用中可以根据允许的装载均匀性要求，设定合适的单次装载量。

为了说明本文提出的动态均匀装载方法的优势，设计了与传统的固定点装载方法的对比仿真实验。传统的固定点装载方法在预先设定的位置连续进行卸料装载作业，待料堆达到预定的高度后，将卸料口移动到下一个装载点继续进行卸料装载，直到所有装载点位置的料堆达到预定高度后结束卸料装载操作，主要应用于联合收获机-运输车协同作业[11]和沥青混凝土装车系统[5,8]。

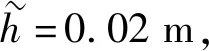
从图10a可以看出，固定点装载方法的高度方差变化曲线分为4段，其中每个转折点表示在该时刻切换了装载点位置，装载的周期数达到823时，固定点装载方法结束装载过程，此后高度方差不再变化。与动态均匀装载方法相比，固定点装载方法的高度方差明显较大，且其装载的周期数823远小于动态均匀装载方法的周期数1 800，即动态均匀装载方法的装载量高于固定点装载方法的2倍。

图10b中，固定点装载方法的重心偏移量初始值较大，虽然在初始阶段粮箱的已装载总量较小，由此产生的力矩较小，但其在更换装载点后重心偏移量下降缓慢，在装载中期产生的力矩较大。在周期数达到823，固定点装载方法结束装载过程时，其重心偏移量降为0，而此时动态均匀装载方法的最大重心偏移量也降至0.2 cm以下，维持在较低水平，在装载过程结束时降为0。即动态均匀装载方法在以重心偏移量进行评价的装载效果也更优。

由此可知，与固定点装载方法相比，动态均匀装载方法能大幅提高粮箱的装载均匀性，提高粮箱的装载量。

图10 固定点装载方法与动态均匀装载方法的装载均匀性变化曲线Fig.10 Evolution diagrams of loading uniformity of fixed points loading and dynamic uniform loading

3 结论

(1)探讨了用于获取粮箱装载状态的三维点云的相机安装位姿，并利用视场增强算法提高了相机视场对粮箱储藏空间的覆盖率。

(2)对粮仓装载状态进行三维点云模型重建，并依据堆体物理模型和相机遮挡模型对盲区进行点云填充，盲区点云估计的平均误差低于5 cm，该方法对粮仓装载状态还原度较高。与常规的粮仓装载状态方法相比，能提供更加全面的装载状态信息。

(3)基于当前的装载状态，提出了以均匀装载为目标的粮箱装载方法。该方法可以用于联合收获机-运输车协同作业的自动控制，为不间断卸料装载过程提供装载位置信息，能提高粮箱装载率与协同作业的效率，同时提高作业过程中车辆行驶的稳定性，降低由于装载不均匀对运输车可能造成的机械损耗，以及由于颠簸发生溢料问题的可能性。

(4)在最高装载高度为0.35 m时，动态均匀装载方法的装载量高于传统固定点装载方法的2倍。该方法不仅提高装载结果的均匀性，还提高了装载过程的均匀性，降低了装载物相互遮挡的可能，从而提高装载过程中装载状态检测的精度。