费控电能表用继电器可靠性评估技术研究

白玉洁 张洁羽 王 丹 宋俊亮 樊浩研 董子慧

（内蒙古电力（集团）有限责任公司电力营销服务与运营管理分公司，内蒙古 呼和浩特 010000）

0 引言

继电器是智能电能表的重要组成部分之一，其作为基础性配套元件被广泛应用于费控领域。当前众多费控电能表生产厂家和研究单位在可靠性预计、可靠性试验以及失效分析等方面进行了对费控电能表用继电器的可靠性评估。但大多是针对其可靠性指标的评估，在评估方法的改进、失效机理分析等方面也开展了一些理论研究工作，而对费控电能表用继电器的现场可靠性评估工作尚未见报道。因此该文针对可靠性预计、可靠性试验等与现场使用存在差异的问题，提出了结合现场数据的可靠性评估方法，建立了相应的费控电能表用继电器可靠性分布模型。

该文通过统计现场失效数据对费控电能表用继电器的可靠性进行评估。将某厂家同批次的费控电能表用继电器现场数据分别进行多种模型的失效分布拟合，以获得最佳失效分布模型，并得到费控电能表用继电器日常使用时的可靠度模型。通过评估结果可更准确地认识费控电能表用继电器的可靠性性能，对厂家的生产、设计有一定的指导意义。

1 继电器失效分析

1.1 现场失效数据

费控电能表用继电器故障前工作时间是指继电器首次处于可用状态直至发生故障的总持续工作时间。应收集继电器使用中（运行中）所有的责任故障应用于可靠性评价中。当该评价批次继电器的责任故障数据量小于30时，则不进行可靠性评价。

1.2 故障分类

产品在运行过程中发生首次工作异常即判断产品失效，费控电能表用继电器的失效分类4类，即：动作类、接触类、噪声类和零部件损坏等。1）动作类。继电器电磁系统通电时不吸合；机械运动阻滞或卡死；线圈损坏断路或短路烧毁。2）接触类。触头在继电器吸合时不通。3）噪声类。继电器通电后，距离继电器前端正前方0.4m处，噪声值超过65dB。4）零部件损坏类。机械零件损坏、断裂或脱落。

1.3 失效数据统计

将继电器所有的故障数据的故障前工作通断次数由小到大排序≤≤…≤a≤…≤a，为总故障数，=1，2，…，。

应用近似中位秩公式计算继电器各故障时间对应的可靠度（）和累计故障概率（），其计算如公式（1）、公式（2）所示。

式中：（）为各故障时间对应的可靠度；（）为累计故障概率；0.3与0.4为常数；为总故障数；为通断次数。

统计得到如表1所示的继电器的可靠度和累计故障概率。

表1 可靠度和累计故障概率的统计结果

1.4 失效数据拟合模型

通过将收集统计得到的现场数据进行模型拟合和模型参数的求解，得到失效分布模型，并获得可靠性指标。常用的可靠性失效分布模型包括双参数指数分布、威布尔分布以及对数正态分布等，具体如下。

双参数指数分布的累计故障概率函数（）如公式（3）所示。

式中：为继电器的故障率；为故障概率函数自变量；为双参数指数分布的位置参数。

威布尔分布的累计故障概率函数（）如公式（4）所示。

式中：为尺度参数；为形状参数。

对数正态分布的累计故障概率函数（）如公式（5）所示。

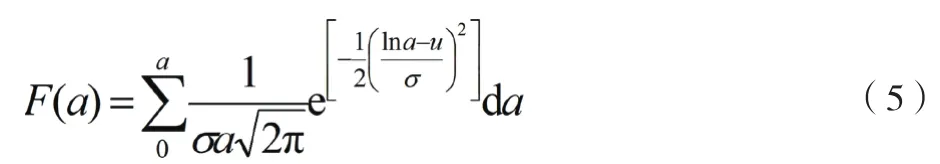
采用最小二乘法对可靠性模型的未知参数进行估计。

1.5 失效分布模型拟合优度检验

原始失效数据的累积失效概率通过拟合优度检验获得其最佳失效分布模型，失效分布模型拟合优度检验常采用Kolmogorov-Smirnov检验法（简称K-S检验法）。

KS检验法是比较一个样本的累积分布函数（）与事先假设的理论分布（）之间的显著性差异是否符合某一水平的衡量方法。首先假设为两个数据分布一致或者数据符合理论分布。实际观测值为=max|（）-（）|，当＞（，）则拒绝，否则则接受假设。其中，（，）为给定样本数n、显著性水平为的拒绝临界值数据表，越小，（，）越小，假设成立的条件越严苛，常见的取值为0.01、0.05等。在该文中（）为近似中位秩公式计算得到累积故障概率函数；（）为拟合得到累积故障概率函数。（，）可通过查KS检验表得到。

通过K-S检验方法对试验数据进行拟合优度检验后的结果可能服从多个失效分布模型，则需要筛选出最佳拟合模型，即可靠性失效分布模型优选。可靠性失效分布模型的优选需要根据残差平方和最小的原则，如公式（6）所示。

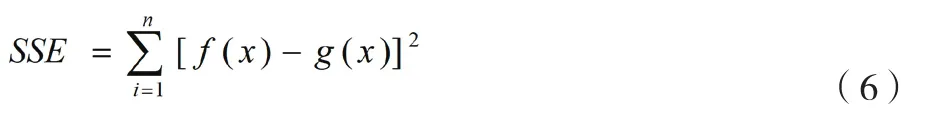
式中：（）为近似中位秩公式计算得到累积故障概率函数；（）为拟合得到累积故障概率函数。为可靠性失效分布模型。

可靠性模型的值越小，模型的拟合效果越好。选择最小值的可靠性模型作为费控电能表用继电器的最优可靠性模型。

2 继电器可靠性模型评价指标

根据得到的费控电能表用继电器的可靠性模型（），评价其可靠性指标。

继电器故障密度函数（）的计算如公式（7）所示。

继电器故障率（）的计算如公式（8）所示。

式中：（）为=时的继电器故障率；（）为继电器故障率函数。

继电器可靠度函数（）的计算如公式（9）所示。

式中：（）为继电器可靠度。

继电器平均故障前时间的计算如公式（10）所示。

对双参数指数分布的可靠性模型，平均故障前时间的计算如公式（11）所示。

式中：为平均故障前时间；为积分常数。

对威布尔分布的可靠性模型，平均故障前时间的计算如公式（12）所示。

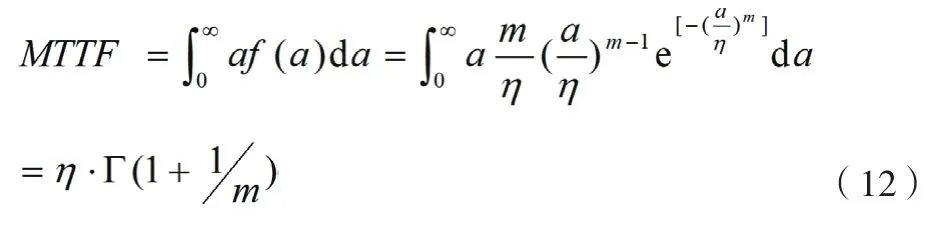
式中：Γ()为伽马函数。

对对数正态分布的可靠性模型，平均故障前时间的计算如公式（13）所示。

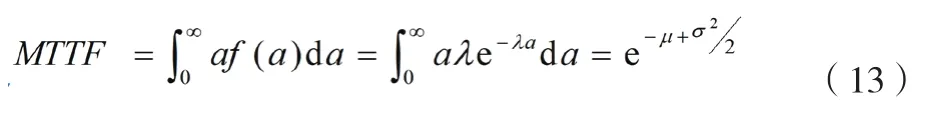
3 统计结果分析

3.1 数据统计

收集统计某一规格型号继电器的使用寿命如表2所示。

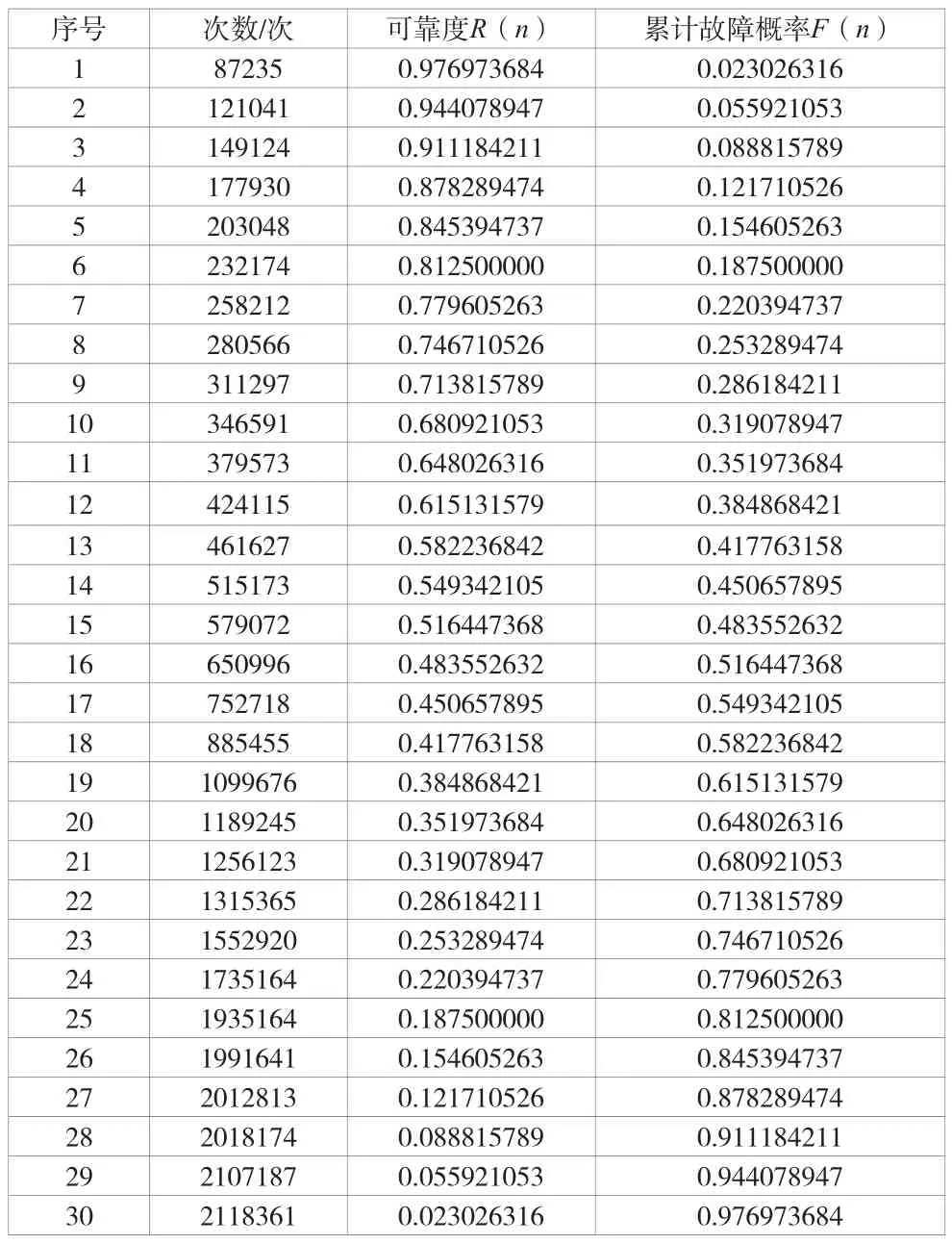
表2 某一规格型号继电器使用寿命统计表

3.2 失效分布模型拟合

根据得到的费控电能表用继电器的故障前时间及其对应的累计故障概率，应用双参数指数分布、威布尔分布、正态分布以及对数正态分布可靠性模型分别对费控电能表用继电器的累计故障概率进行拟合，获取可靠性模型的未知参数。

双参数指数分布的累计故障概率函数（）如公式（14）所示。

式中：为费控电能表用继电器的故障率；为双参数指数分布的未知参数。

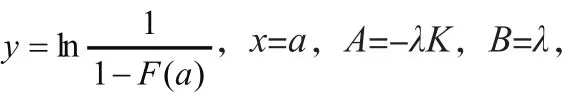
其中l、l如公式（16）、公式（17）所示。

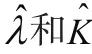
其双参数指数分布的参数估计过程如表3所示。

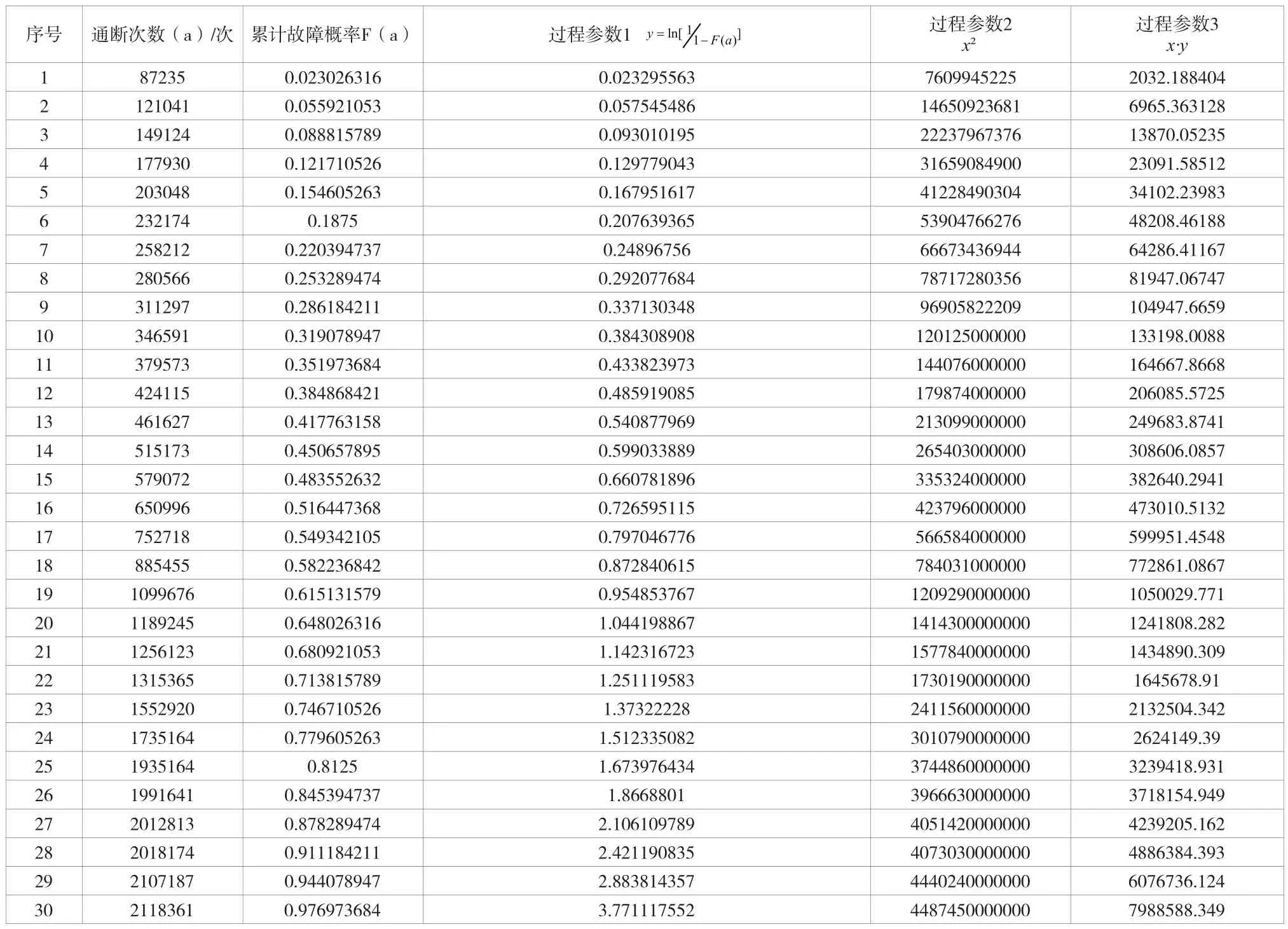
表3 双参数指数分布的参数估计过程表

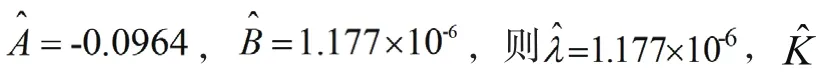
威布尔分布的累计故障概率函数（）如公式（20）所示。

式中：为尺度参数；为形状参数。

采用最小二乘法对威布尔分布的未知参数进行估计。

对公式（20）进行变换，可得公式（21）。

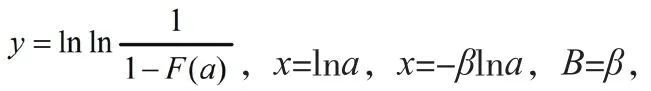
其中l、l如公式（24）、公式（25）所示。

最终，得到尺度参数和形状参数的估计值ˆ和ˆ分别如公式（26）、公式（27）所示。

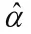
其威布尔分布的参数估计过程如表4所示。

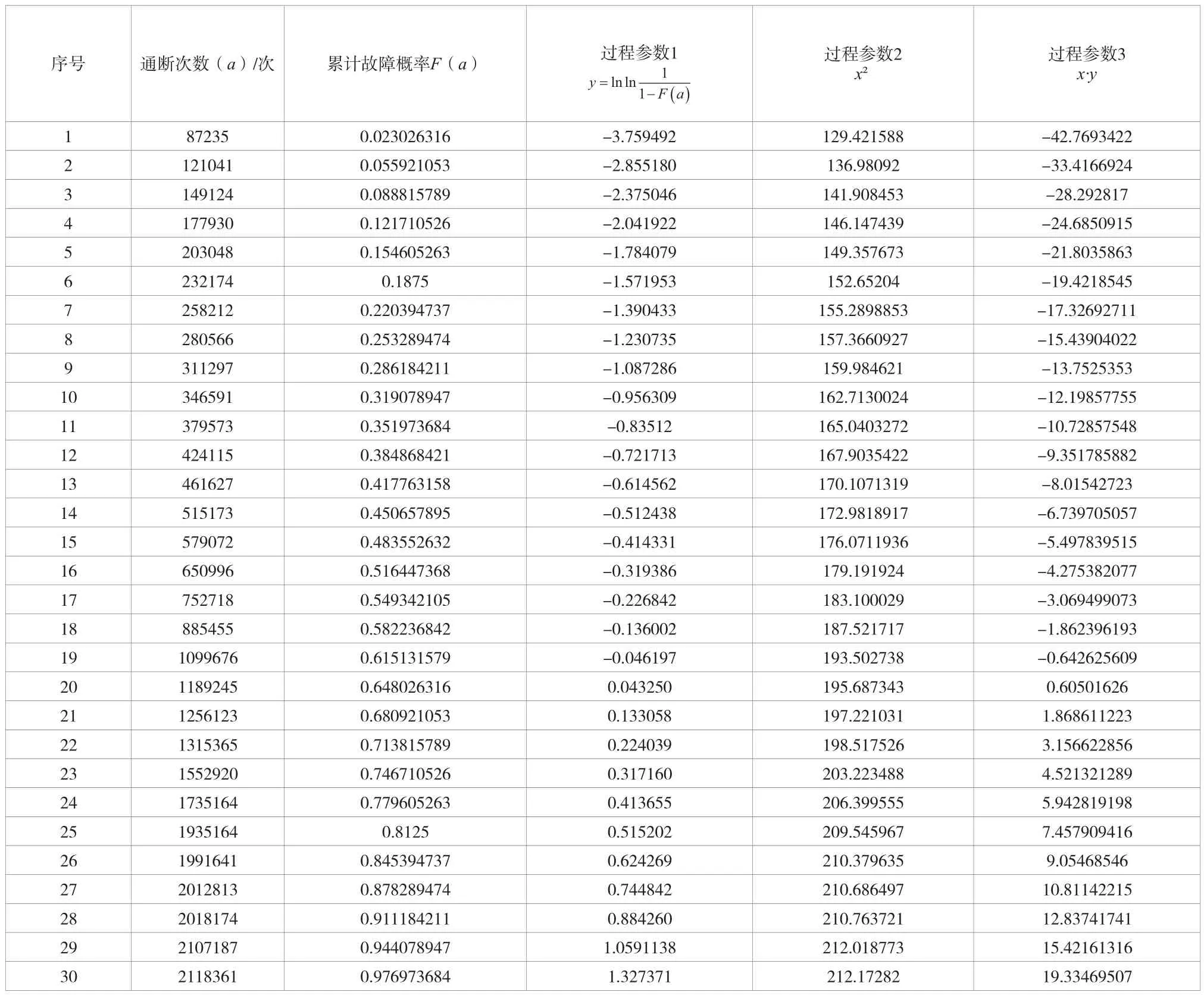
表4 威布尔分布的参数估计过程

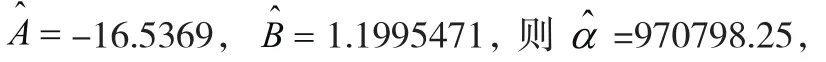
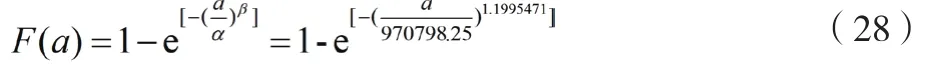
对数正态分布的累计故障概率函数（）如公式（29）所示。

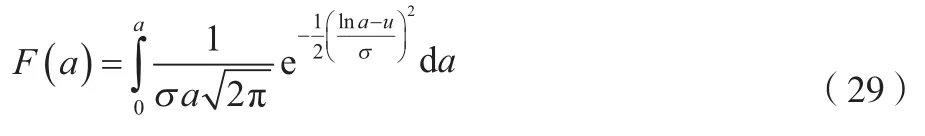
式中：为对数均值；为对数标准差。

同样，采用最小二乘法对对数正态分布的未知参数进行估计。

累计故障概率函数变换，可得公式（30）。

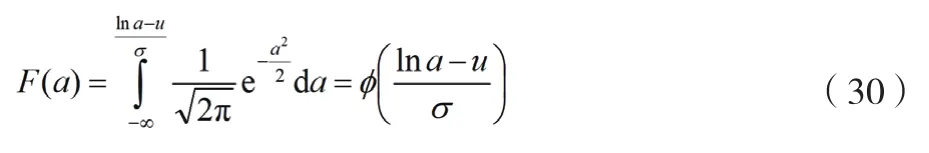
由于标准正态分布函数（）是严格单调上升的，故其存在反函数，且反函数如公式（31）所示。

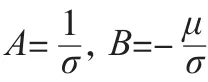
其中l、l如公式（34）、公式（35）所示。

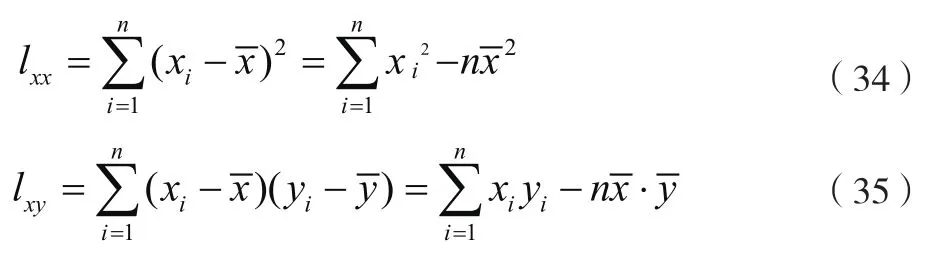
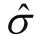
其对数正态分布的参数估计过程如表5所示。

表5 对数正态分布的参数估计过程

4 可靠性模型拟合优度检验

可靠性模型拟合优度检验采用Kolmogorov-Smirnov检验法。原假设：近似中位秩公式计算得到累积故障概率函数F（）=拟合得到累积故障概率函数（）。近似中位秩公式计算得到累积故障概率函数和拟合得到累积故障概率函数之间的最大偏差D可由公式（39）求得。

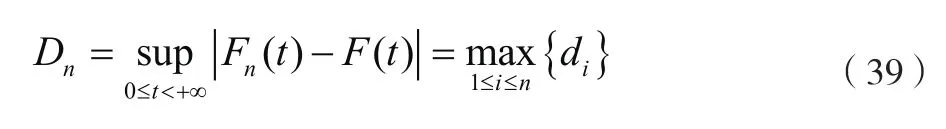
给定显著性水平，样本数量为时，根据标准K-S检验临界值表得到临界值D。当D＜D时，接受原假设；反之则拒绝。

4.1 双参数指数分布拟合优度检验

双参数指数分布拟合优度检验的过程如表6所示。根据标准K-S检验临界值表，样本数量取30，显著性水平=0.01，得D=0.29，即有公式（40）。

表6 双参数指数分布拟合优度检验的过程

通过拟合优度检验，可认为双参数指数分布拟合结果满足要求。

4.2 威布尔分布拟合优度检验

威布尔分布拟合优度检验的过程如表7所示。

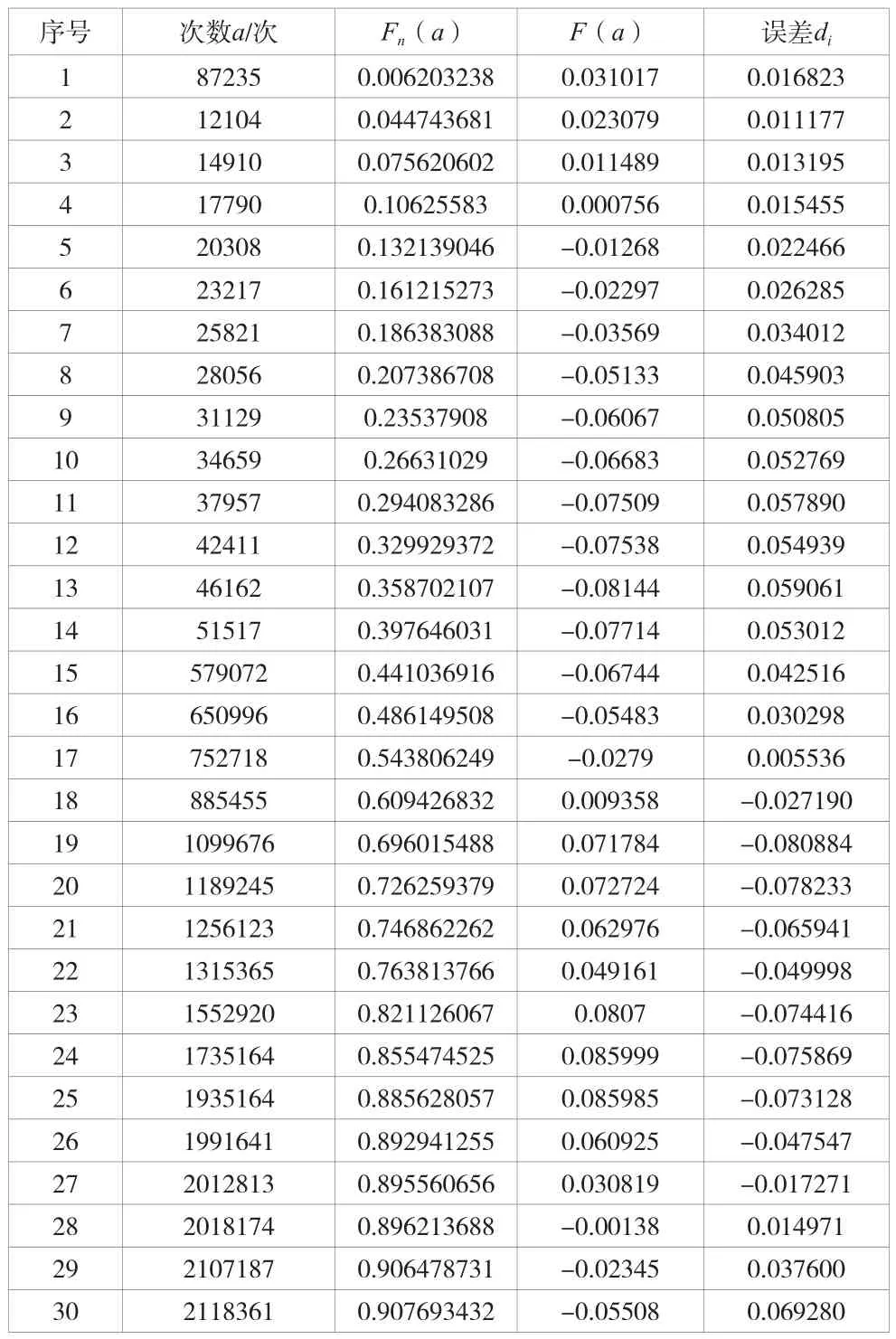
表7 威布尔分布拟合优度检验的过程

根据标准K-S检验临界值表，样本数量取30，显著性水平=0.01，得D=0.29，即有公式（41）。

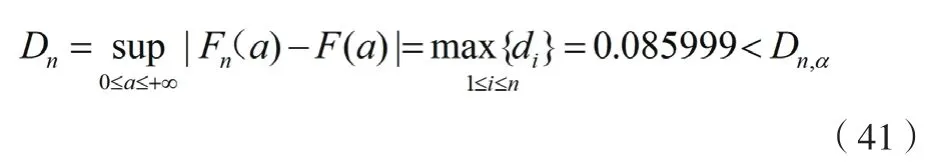
通过拟合优度检验，可认为威布尔分布拟合结果满足要求。

4.3 对数正态分布拟合优度检验

对数正态分布拟合优度检验的过程如表8所示。

表8 对数正态分布拟合优度检验的过程

根据标准K-S检验临界值表，样本数量取30，显著性水平=0.01，得D=0.29，即有公式（42）。

通过拟合优度检验，可认为对数正态分布拟合结果满足要求。

5 可靠性模型的优选

采用残差平方和最小的方式进行可靠性模型的优选。其残差平方和如公式（43）所示。

可靠性模型的值越小，模型的拟合效果越好。选择最小值的可靠性模型作为智能电能表的最优可靠性模型。

以第4节中的示例数据为例，进行可靠性模型的优选。

各个可靠性模型的残差平方和如表9所示。

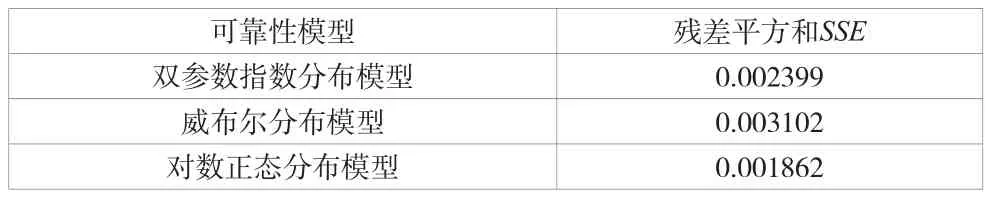
表9 各个可靠性模型的残差平方和

可见残差平方和最小的为对数正态分布模型，因此，对数正态分布模型为最优可靠性模型，如公式（44）所示。

6 结语

该文对费控电能表用继电器的可靠性进行了评估。通过记录继电器失效的数据，对失效数据的失效分布进行了双参数指数分布、威布尔分布和对数正态分布模型的拟合优度检验，根据最优筛选方式发现费控电能表用继电器失效最符合双参数指数分布，并在此基础上获得了费控电能表用继电器的失效分布。相关生产厂家可根据继电器的可靠性模型对继电器的可靠性进行评估，也可借鉴该文给出的数据处理方法对继电器进行质量控制，其对提升费控电能表用继电器的可靠性有积极作用。