双滑块驱动无返回力矩钟表机构特性仿真研究

黄凤军 郭浩洋 徐姝苇 郭 永 张 攀

（1.海军装备部，山西 侯马 043000； 2.淮海工业集团有限公司，山西 长治 046012）

0 引言

由于全电子引信在抗干扰方面的性能较弱，因此钟表机构延时引信逐渐又被重新关注。因为火药延期时间散布大且不适于长期贮存，所以无法用于精度较高的延时引信。无返回力矩钟表机构是引信安全系统中非常重要的延时机构，在炮弹、导弹等装备的安全和解除保险机构中常用双滑块驱动无返回力矩钟表机构（识别装备发动机的过载），将其作为安全和解除保险机构具备延时功能的第一道机械保险。双滑块驱动无返回力矩钟表机构具有延期解除保险性能，能够提供与弹道环境相关的基本安全距离，以提高安全性和可靠性。该文对双滑块驱动无返回力矩钟表机构进行物理建模和仿真，研究它在发动机过载情况下的延期解除保险时间。

1 物理模型

无返回力矩钟表机构有很多种模型。主要有离心原动机驱动的无返回力矩钟表机构和惯性原动机驱动的无返回力矩钟表机构，该文采用的是Overman D.L.提出的惯性原动机驱动的无返回力矩钟表机构的模型，该模型将双滑块作为原动机驱动，将阻尼器作为传动轮系和擒纵机构，研究在阻尼作用下原动机的运动特性。根据该理论建立的物理模型，如图1所示。

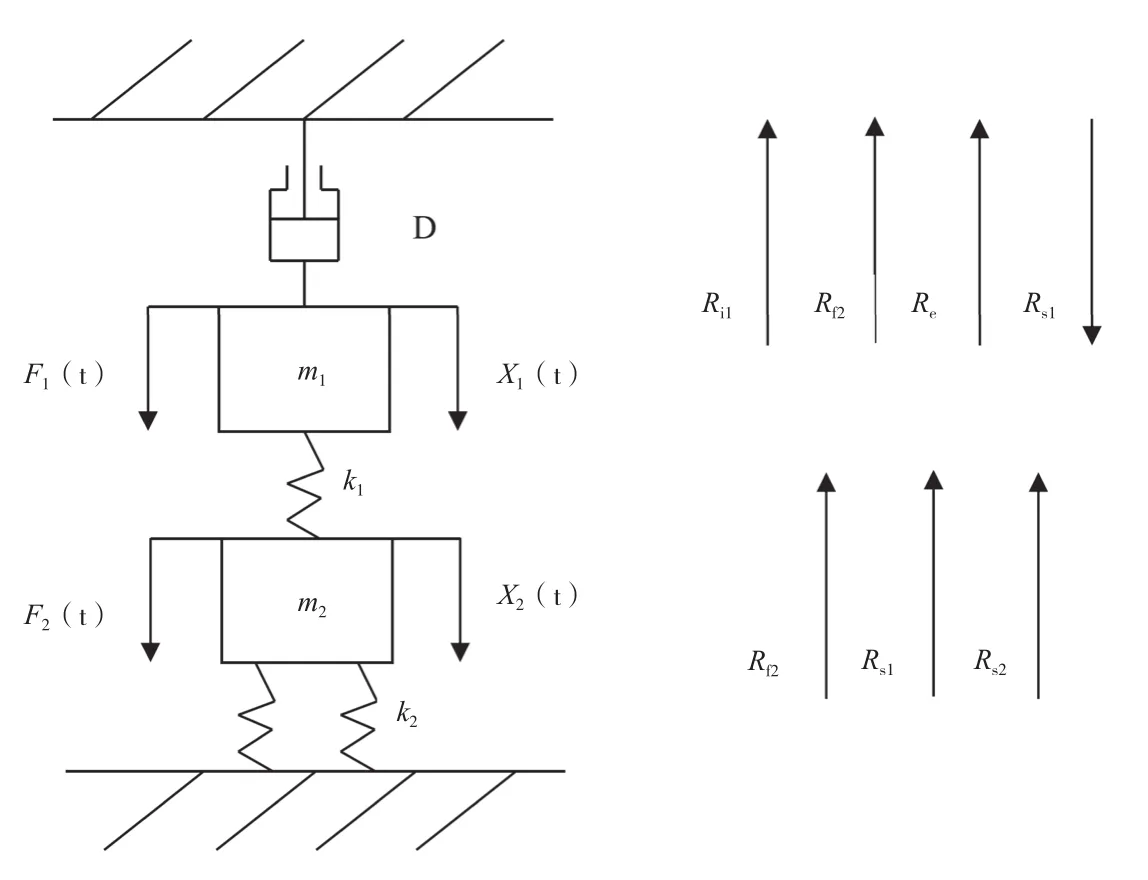
图1 双滑块驱动钟表机构物理模型

根据牛顿第二定律∑=，对上滑块来说，有公式（1）。

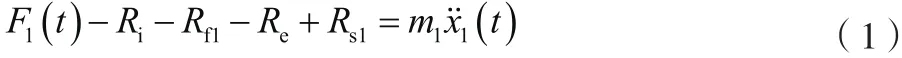
对下滑块来说，有公式（2）。

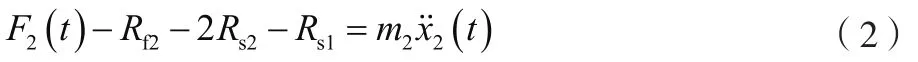
公式（1）、公式（2）为研究直线惯性原动机驱动无返回力矩钟表机构运动特性的依据，直线惯性原动机即由上、下滑块组成的双滑块。

2 双滑块（惯性原动机）驱动的无返回力矩钟表机构数学模型

以双滑块作为惯性原动机对象，阻尼为滑块运动过程中传动轮系及擒纵机构的作用，根据离心原动机驱动的无返回力矩钟表机构动力学模型可以列出上、下2个滑块的动力学方程，如公式（3）、公式（4）所示。

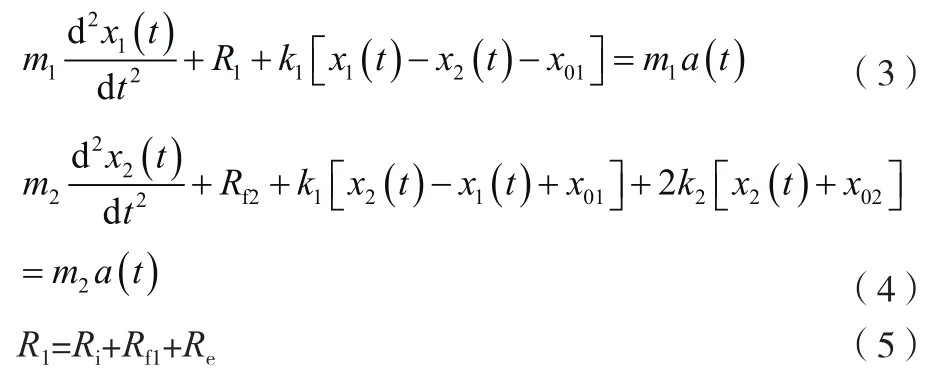
式中：（）为惯性体的加速度过载；为上滑块的质量；为下滑块的质量；为拉簧的刚度；为惯性簧的刚度；为拉簧的预拉变形；为惯性簧的预压变形；（）为上滑块位移；（）为下滑块位移；为传动轮系及擒纵机构引起的惯性阻力；为擒纵机构运动引起的阻力；为各种滚动摩擦、传动啮合引起的阻力；为滚动摩擦引起的阻力。

根据Overman D.L.的《Analysis of M125 Booster Mechanism》可得公式（6）～公式（10）。

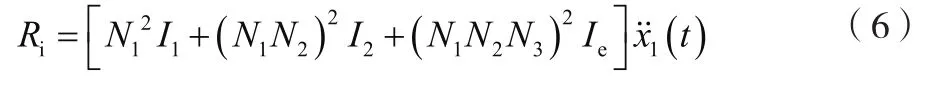
式中：为第一过渡轮齿轴与齿条的传动比；为第二过渡轮齿轴与第一过渡轮的传动比；为第一过渡轮转动惯量；为第二过渡轮转动惯量；为擒纵轮转动惯量。

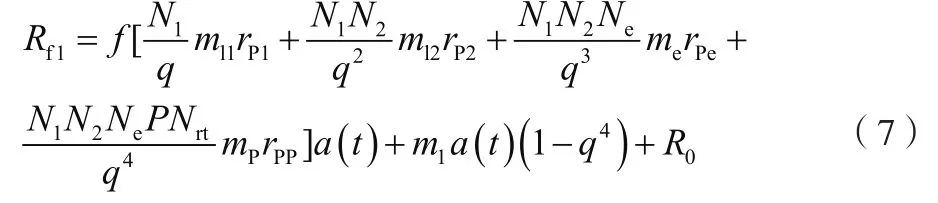
式中：为滚动摩擦系数；为平衡摆与擒纵轮的啮合百分比；为齿条、齿轮与齿轮间啮合效率；为第一过渡轮轮轴半径；为第二过渡轮轮轴半径；为擒纵轮轮轴半径；为摆轮轮轴半径；为擒纵轮的质量；为摆轮的质量；为第一过渡轮的质量；为第二过渡轮的质量；为钟表机构的最小驱动阻力。

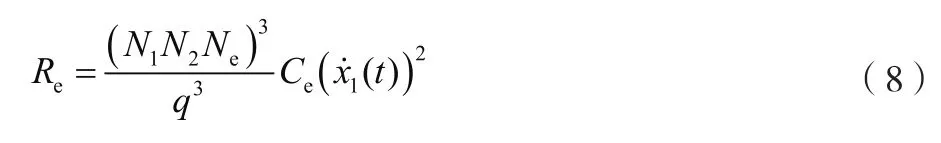
式中：为擒纵轮齿轴与第二过渡轮片的传动比；为擒纵轮的阻尼系数。

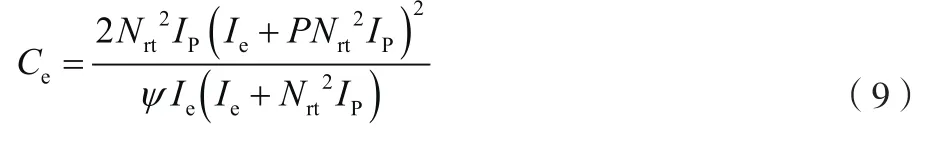
式中：摆轮对擒纵轮的平均传动比；为摆轮转动惯量；为擒纵轮齿每齿对应的半角。

在现代控制理论中，球杆系统是一个经典的控制系统研究对象(图1)，由于其非线性特性及开环系统的不稳定性，球杆系统实验装置可应用于控制理论及方法的研究[1]。对于球杆系统的建模过程以及闭环系统控制器的设计，仍有着许多可研究的角度和方法。

考虑2个滑块质量及传动轮系惯量后擒纵轮的有效惯量如公式（11）所示。

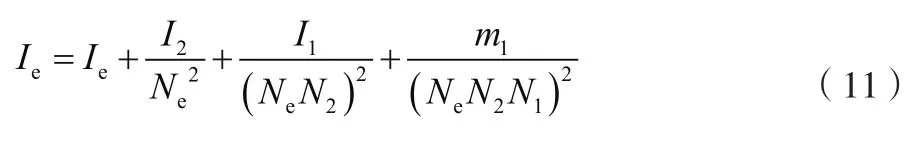
将公式（5）～公式（11）合并，代入公式（3）并简化，可得到公式（12）、公式（13）。

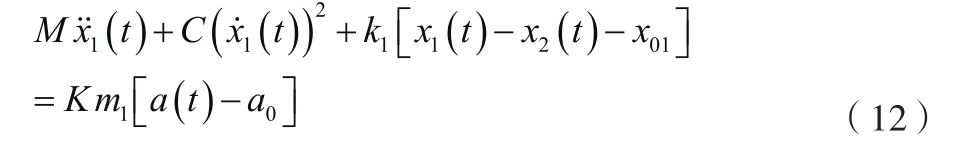
式中：为上滑块有效质量；为效率系数；为速度阻尼系数。

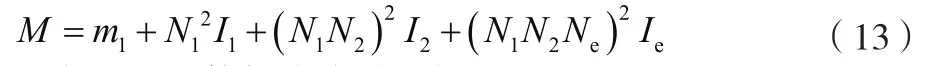
速度阻尼系数如公式（14）所示。

因滚动摩擦和啮合效率而形成的驱动效率系数如公式（15）所示。

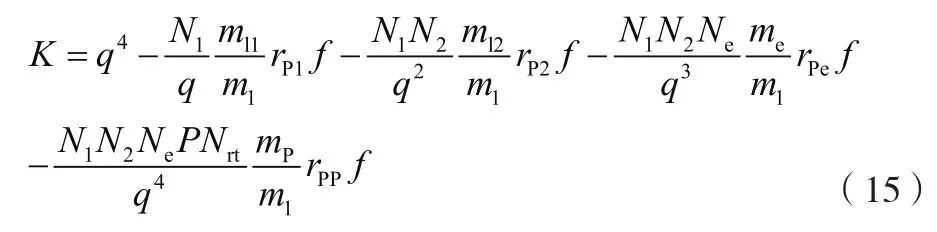
无返回力矩钟表机构最低驱动力如公式（16）所示。

3 计算机仿真求解

3.1 三维立体建模

采用三维建模软件Inventor建立机械惯性保险机构所有零件的虚拟模型并进行样机装配，在Inventor环境下，将零件属性定义好，开展运动学仿真，检查零件之间是否有干涉。

3.2 发动机过载曲线

采用某典型发动机的高温、低温以及常温过载数据绘成的曲线如图2所示。为了简单起见，取25.0 g、28.5 g以及32.0 g的阶跃信号作为机械惯性保险机构仿真的激励信号。

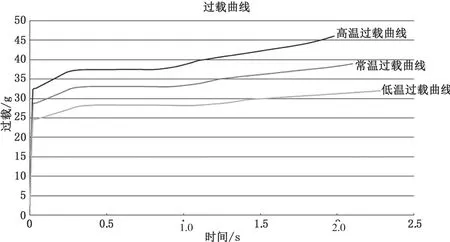
图2 发动机过载曲线图

3.3 在visualNastran环境下仿真

将Inventor三维模型导入动力学仿真软件visualNastran环境下，定义相互之间的约束关系，将高温过载曲线作为激励进行机械惯性保险机构动力学仿真，从而得到各个零部件的运动参数，上、下滑块位移参数如图3、图4所示。

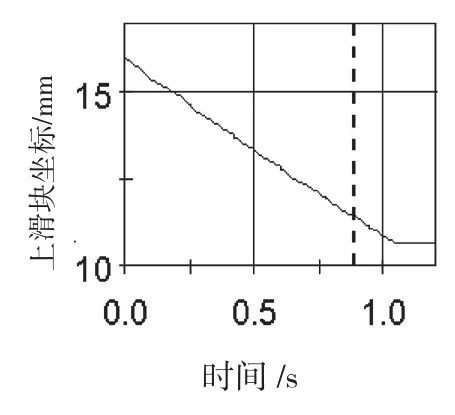
图3 上滑块位移曲线

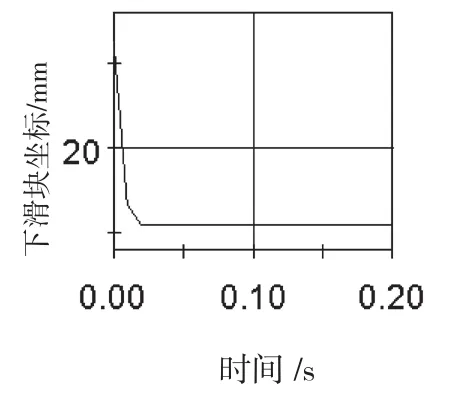
图4 下滑块位移曲线

留一定余量，取高温过载的下限值32.0 g进行仿真，由图4可知，在施加过载后，机械惯性保险机构下滑块由启动到运动到位仅用了0.02 ms，在模拟的弹簧拉力作用下，机械惯性保险机构上滑块由启动到下滑运动到位时解除保险，下滑块坐标由22.500 mm变为17.915 mm，上滑块坐标由15.900 mm变为11.320 mm，此时上、下滑块位移均为4.580 mm，对应的解除保险时间为0.88 s，对应装备飞行距离为121 m。

将常温过载曲线作为激励，取常温过载的下限值28.5 g进行机械惯性保险机构动力学仿真，在施加过载后，机械惯性保险机构下滑块迅速运动到位，机械惯性保险机构上滑块下滑到位时解除保险，得到上、下滑块的位移曲线，由仿真的曲线可知，此时上、下滑块位移均为4.58 mm，对应的解除保险时间为0.90 s，对应装备飞行距离约为113 m。

将低温过载曲线作为激励，取低温过载的下限值25.0 g进行机械惯性保险机构动力学仿真，在施加过载后，机械惯性保险机构下滑块迅速运动到位，机械惯性保险机构上滑块下滑到位时解除保险，得到上、下滑块的位移曲线，由仿真的曲线可知，此时上、下滑块位移均为4.58 mm，对应的解除保险时间为0.92 s，对应装备飞行距离约为104 m。

勤务处理是指弹药在发射前经历的所有过程，包括搬运、运输、贮存、安装、装定和装填等过程。在整个过程中，引信会受到振动、冲击和撞击，引信零件除了受到直接的撞击力外，还会因振动和冲击所产生的相对引信体的冲击惯性力，当力的方向与引信零件解除保险运动方向一致时，这些力的危害最大。下面对勤务处理过程中可能遇到的跌落、冲击和振动进行仿真。

对勤务处理中的跌落试验进行仿真，当安全和解除保险机构自高度为1.5 m的地方自由落体至钢板时，受到的冲击瞬时过载峰值为13 000.0 g，持续时间为370 μs。将跌落冲击过载作为机械惯性保险机构的激励进行仿真，由得出的仿真曲线可知，机械惯性保险机构在受跌落冲击过载时下滑块很快运动到位，但上滑块几乎不动，机械惯性保险机构不能解除保险，因此可以很好地满足平时勤务处理中对安全性的要求。

在勤务处理中，安全和解除保险机构另一个主要的干扰力为运输中的冲击和振动。根据《引信环境试验》（GJB 573A—1998）的要求，在振动台上模拟运输中的冲击和振动，振动正弦曲线为峰值280.0 g，持续时间为2 ms的半正弦，间隔2 s。在一个半波冲击后，惯性钟表机构足以恢复到初始状态。为简单起见，以方波代替半正弦波作为机械惯性保险机构的激励进行仿真，由得出的仿真曲线可知，在振动曲线激励下，机械惯性保险机构的下滑块很快运动到位，但上滑块位移很小，仿真曲线与1.5 m跌落试验仿真曲线类似，几乎不动，此时机械惯性保险机构不能解除保险，可以很好地满足平时勤务处理中对安全性的要求。

4 结语

对正常发动机过载和勤务处理进行仿真分析，仿真分析结论如下：1） 机械惯性保险机构能够区分正常发动机过载和勤务处理的干扰力。2） 当在各种温度条件下发动机出现预定过载时，机械惯性保险机构均能解除保险，此时上滑块的位移4.58 mm。3） 在高温、常温以及低温发动机过载下，机械惯性保险机构解除保险的时间相差很小，因此它是一个机械定时器，能够给装备提供一个基本安全距离，约为104 m～121 m。4） 通过计算机仿真调整上、下滑块的质量比、惯性簧、拉簧之间的匹配关系以及它们在不同发射过载条件下的运动规律，还可以进一步调整机械延期解除保险时间。