复杂地形风电场尾流影响规律研究

王 欣 李 超 刘伟江

（1.浙江运达风电股份有限公司技术中心，浙江 杭州 310012；2.浙江省风力发电技术重点实验室，浙江 杭州 311100；3.水利部产品质量标准研究所 规划咨询处，浙江 杭州 310024）

0 引言

复杂地形风电场尾流效应仿真的准确性直接影响风电场微观选址的可靠性。针对风电场尾流影响分析，丹麦学者MIKKELSEN基于BEM（blade element momentum）理论提出制动模型，与线性叠加理论相比，该模型提高了尾流计算的精度，国内外学者基于该思路延伸出制动盘、制动线以及制动面模型。欧洲盲测报告曾指出，与只考虑湍动能的一方程模型相比，考虑湍动能和湍流耗散率的两方程模型可以更准确地捕捉大气边界层流动。WAKES等人以中尺度或二维模拟结果作为三维流体域的边界条件，该方法能使入口边界来流风况得到充分发展，增大了计算域。大气边界层流动仿真是复杂地形流动仿真的难点，国内外学者对该问题进行了大量研究，并基于CFD提出了精细化仿真方法。

该文结合三维Navier-Stokes（N-S）方程和制动盘模型，并对大气热稳定度的影响进行计算，从而建立了可精确模拟包括风力机尾流和大气边界层流动的复杂地形风电场尾流效应计算的方法。同时，以某实际复杂地形风电场作为分析对象，对受尾流影响的风力机前后流场特性进行数值计算，通过与实际运行数据进行对比，验证了该文所建立的计算方法的准确性。

1 计算方法

1.1 制动盘模型

假设大气为单相干空气，不考虑大气中的尘粒和水汽。因此，该仿真求解定常、单相和三维不可压缩雷诺时均N-S方程（简称为RANS）。气流经过叶轮时受轴向的阻力和切向的诱导力作用，在该计算所采用的制动盘模型中忽略切向力和尾流旋转效应，采用轴向阻力形成的压差来描述叶轮在流场中的作用。

叶轮前后压差如公式（1）所示。

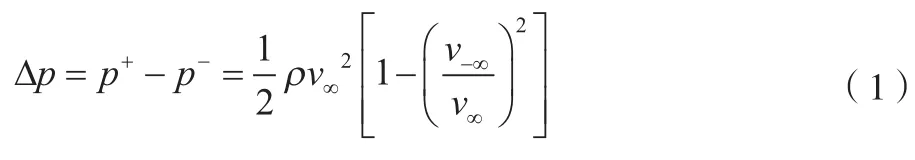
式中：Δ为叶轮前后压差；为叶轮后压力；为叶轮前压力；为空气密度；为来流速度；为叶轮后速度。

经过转换和推导，公式（1）可表述为公式（2）。

式中：C为推力系数。

可以根据来流风速和推力曲线获得C，在计算时不考虑风剪切和叶片径向气动变化对C的影响。该计算根据风轮前端的风速变化并结合推力曲线动态计算体积力源项。在数值计算时，通过迭代求解添加了体积力源项的动量方程，以实现叶轮对气流的作用。

1.2 求解器

该计算以OpenFOAM中内置两方程的simpleFoam求解器为基础进行二次开发，添加了基于Monin-Obukhov长度的浮力相关计算。simpleFoam采用压力速度耦合的Simple算法，求解思路如下：1） 根据初始压力求解离散动量方程，获得初始速度。2） 因为初始速度无法满足连续方程，所以构建压力修正量。3） 修正后的压力通过动量方程获得修正后的速度。重复上述过程，直到速度满足连续方程就可以完成迭代。仿真采用有限体积法在空间上对控制方程进行离散。在离散格式中，gradSchemes采用Gauss linear，divSchemes采用Gauss upwind，laplacianSchemes采用Guass linear corrected。

1.3 计算域及网格处理

计算域如图1所示，以机组WT#8为圆心截取5km×5km的地形范围，计算域高度为1.2 km。采用二维模拟结果作为三维流体域的边界条件，使来流到达对象区域时已形成稳定风况。

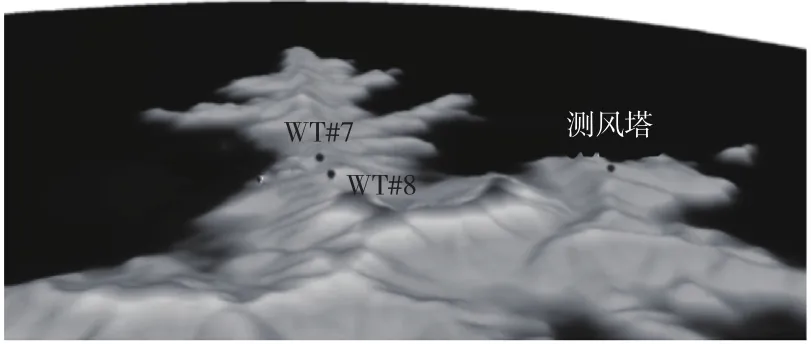
图1 计算域及机组排布

计算网格采用OpenFOAM软件内的blockMesh模块创建。高度方向grading参数给定90，网格高度0.3 m，对制动盘所在区域进行3次加密处理，总网格数为1.5×10。

1.4 计算设置

来流入口边界条件采用考虑地表粗糙度高度（）和Monin-Obukhov 长度（）的修正对数风廓线（），如公式（3）所示。

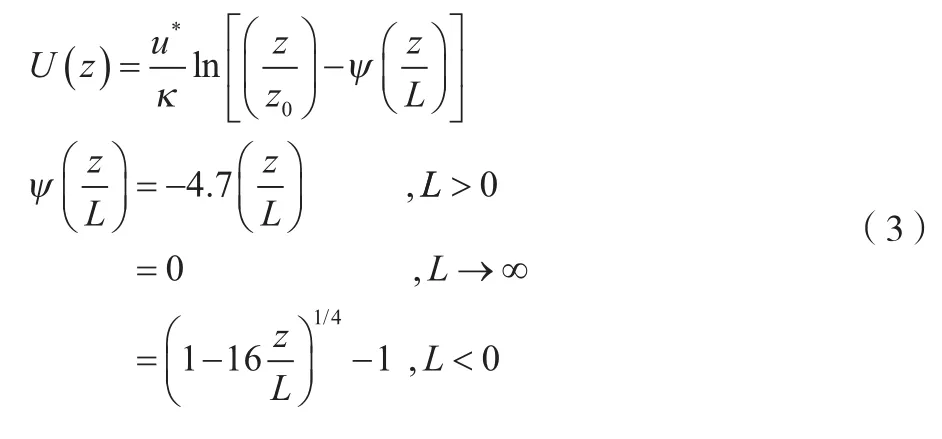
式中：为地表粗糙度长度；为垂直高度；为地表摩擦速度；为von Karman数，在该计算中=0.41；为经验公式，无实际物理意义。

入口边界湍动能及耗散率如公式（4）、公式（5）所示。

式中：C为经验常数，C=0.09。

计算域顶部边界条件选择压力0和速度-；计算域底部边界选择壁面函数；利用decomposePar模块对计算域进行分块，分配到计算机的多核心同步求解。

2 实例验证

2.1 结果验证

对机舱风速风向仪记录的数据进行风向切片统计，建立尾流影响扇区（343 °～353 °）WT#7和WT#8机组处的风速散点统计关系，如图2所示。采用WT#7机组机舱风速作为WT#7机组来流风速，WT#8机组机舱风速作为WT#7机组尾流区风速。

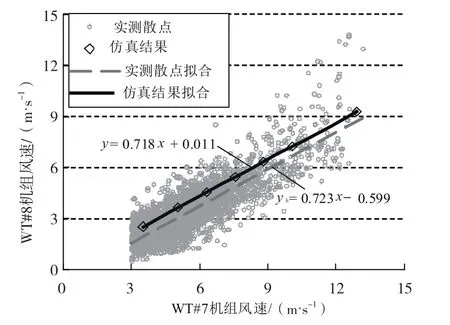
图2 WT#7机组和WT#8机组处风速比

散点拟合给出WT#7机组实测风轮前后风速关系式，2点的风速比为0.723。基于仿真计算结果拟合2点的风速比为0.718，绝对误差为0.005。

机舱风速测量点位于风轮后方，受叶轮影响，该位置的风速小于叶轮前端的风速，同时存在数值误差和散点拟合误差。因此导致实测结果曲线和仿真结果曲线存在一定偏移。

2.2 大气热稳定度影响分析

在风电场流动仿真分析过程中的大气热稳定度往往被假设为中性，其代表的热效应被忽略。大气热稳定度可分为稳态（stable）、中性（neutral）以及非稳态（unstable）3种状态类型。在不同状态下的地表与大气温差会导致大气在垂直方向上存在不同的对流形态，该垂直方向上的作用力导致气流贴地流动发生变化，尤其在遇到障碍后。在低风速复杂地形上，空气流动缓慢且受起伏地形影响易形成持续漩涡，垂直方向上的浮力作用影响将变得显著。

不同热稳定度下大气边界层的流动状态如图3所示。区域1为来流平坦区域，热稳定度未产生较明显影响，在稳态、中性以及非稳态3种状态下气流呈相似的贴地流动。区域2为气流在起伏山地上流动，此时气流贴地流动性变差，并伴有减速现象，低速区域影响范围在长度上呈现非稳态＞中性＞稳态的规律。区域3为背风面平坦区域，气流流经山地后在该区域呈现明显的分层现象，且向斜上方飞逸，低速区域影响范围在高度上同样呈现非稳态＞中性＞稳态的规律。

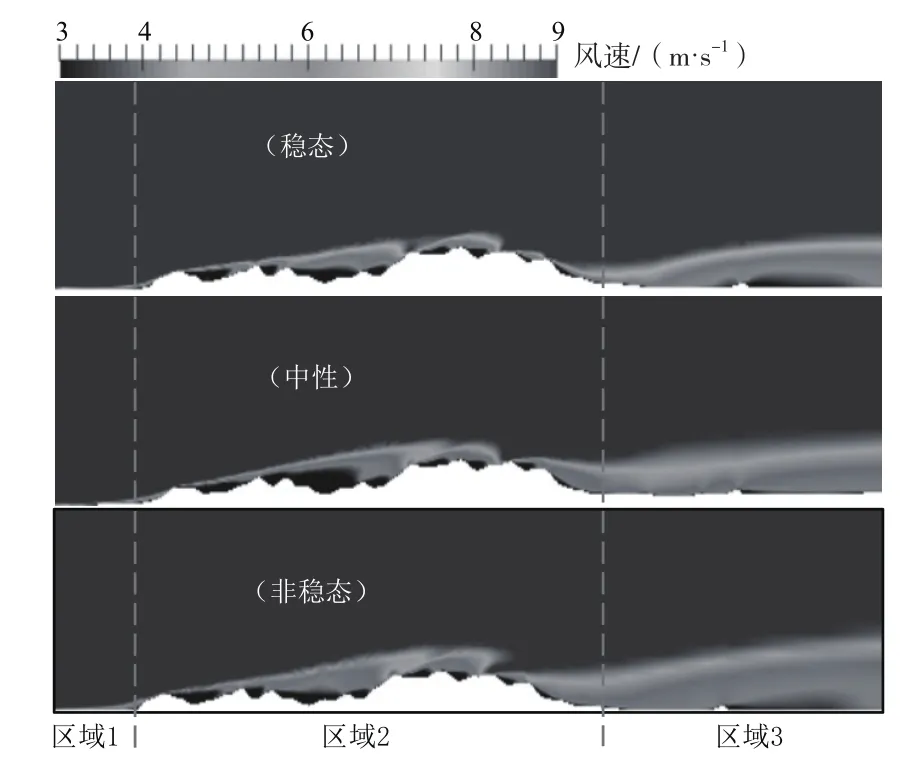
图3 不同热稳定度下风速分布图

2.3 尾流影响分析

在中性情况下，尾流区风速分布如图4所示，在WT#7机位点的山坡后面出现了1个低风速区。WT#8机组不仅受WT#7的尾流影响，而且还受该低风速区的影响。

图5对图4中制动盘前后0.8（为机组风轮直径）距离的4个位置（P、P、P以及P）进行风廓线取样分析。由图5可知，当高度高于150 m时，速度出现阶梯形不光滑分布，这是由该高度网格分辨率开始降低引起的。该高度已高于制动盘高度（制动盘相对高度为38 m～113 m），并不影响结果分析。

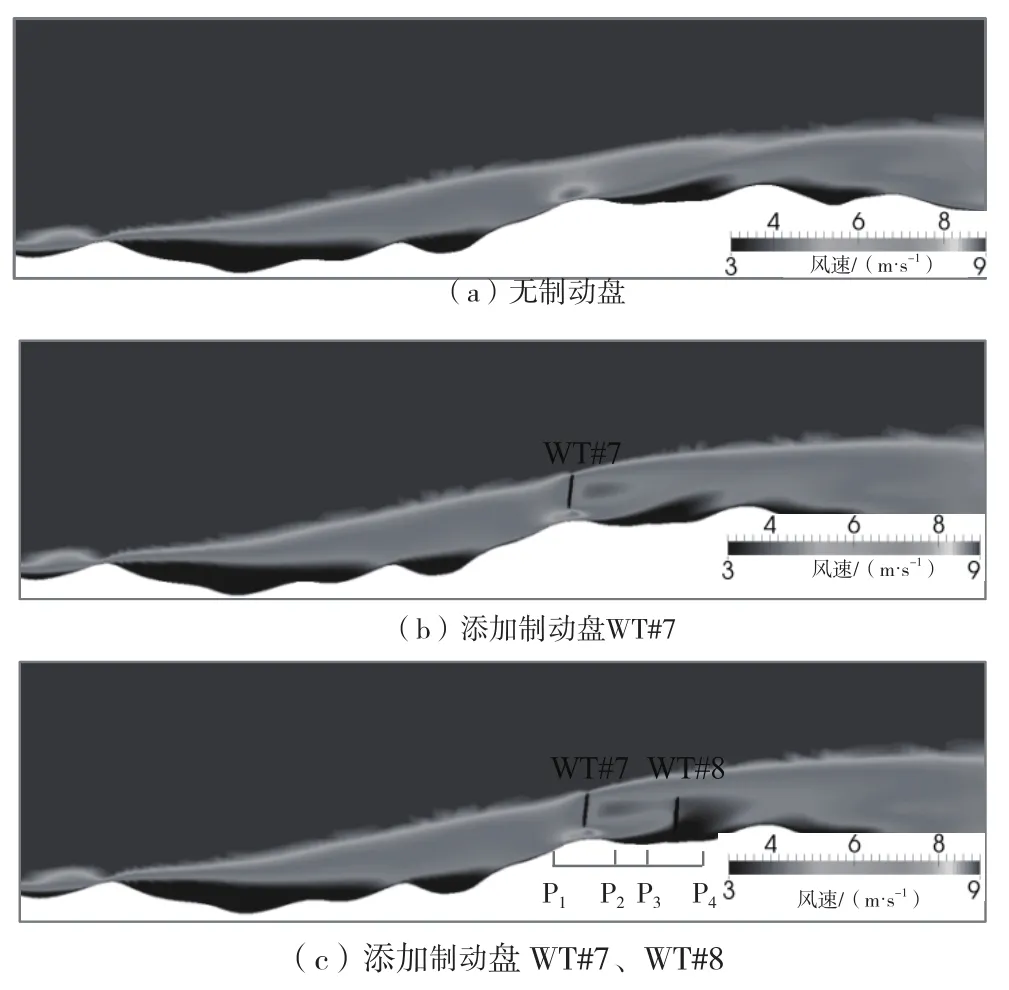
图4 尾流影响下风速分布（中性）

图5（a）给出了来流风况特性。随着相对高度的增加，风速快速增大，在高度约为10 m～11 m附近达到7.0 m/s～7.5 m/s。当相对高度为15 m～200 m时，前方山峰影响带的作用显著，风廓线风速呈降低的状态。随着高度的进一步增加，脱离了影响带的作用，风廓线风速回升并稳定在11.3 m/s。

由图5（a）和图5（c）可知，在添加制动盘后，风廓线在制动盘前端呈现微小的风速降低的现象，这与理论上风轮前端诱导区出现风速减弱的特性相符，说明了该制动盘模型的准确性。在复杂地形上，风廓线并不按标准的对数正态分布。由于山坡对来流的阻挡，在坡后方贴近地表处形成低速区。由图5（c）可知，在没有制动盘的情况下，P位置的风廓线呈“S”形。

由图5（b）～图5（d）可知，在制动盘对应高度下，风廓线出现明显的风速衰减段。当复杂地形影响和尾流影响叠加时，风廓线的“S”形分布更加明显，且风速衰减段在高度上的相对位置发生相应变化。

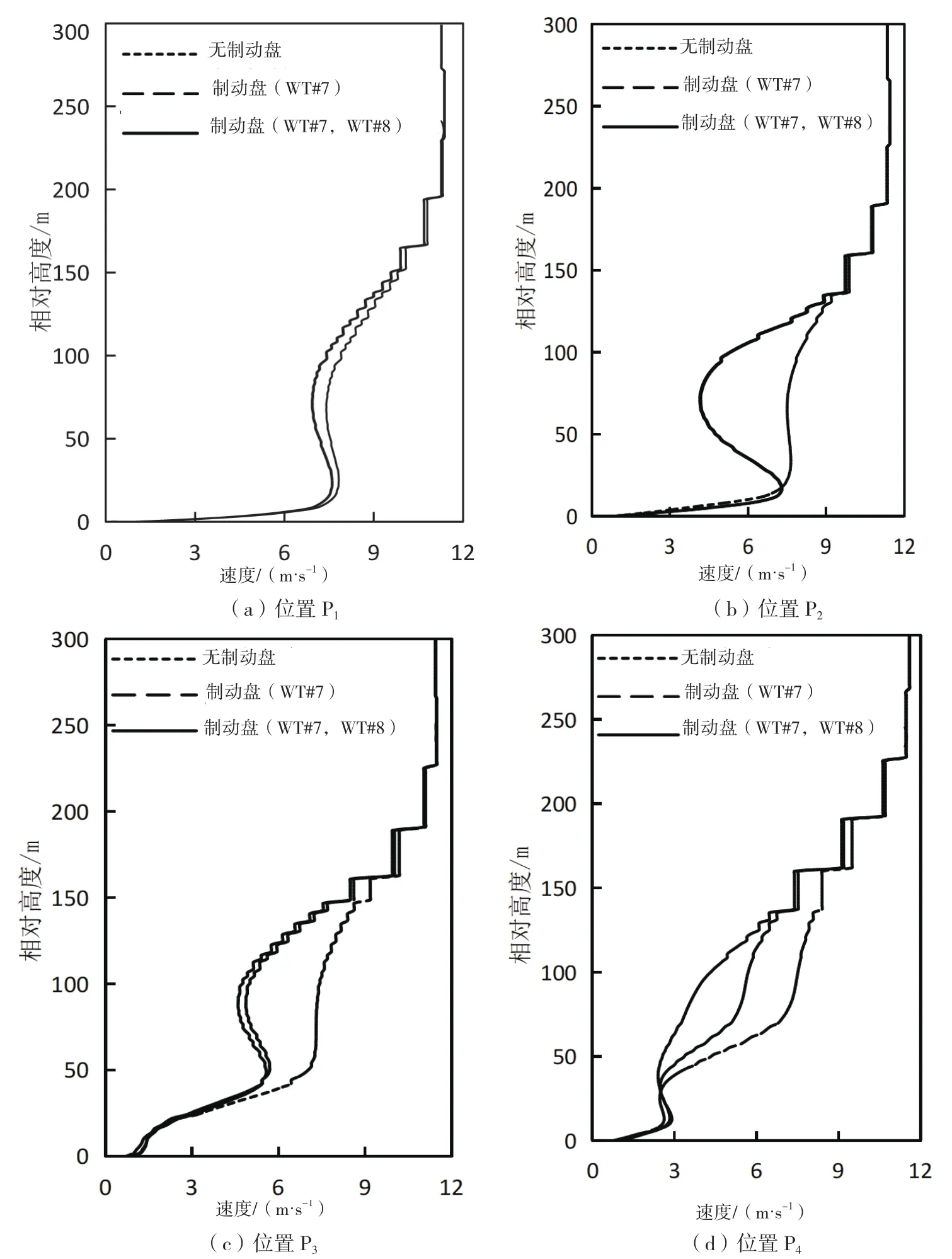
图5 制动盘周围风廓线（中性）

3 结语

目前，国内风电行业存在复杂地形风资源计算不准确的问题，该文基于三维N-S方程和制动盘模型建立了精细化尾流数值仿真方法，分析了在地形、尾流和大气状态共同作用下的流动特性，并采用实际运行数据验证了该方法的准确性。

该文对大气热稳定度的影响进行了分析，说明了在复杂地形上近地面流动存在分层现象，且与大气热稳定度具有相关性。同时，由于受地形的影响，因此到达风力机的风廓线呈现出明显的“S”形分布，与平坦地形上的标准对数正态分布有较大区别。