往复节流式正脉冲发生器性能分析

朱泽旭，余 鲲，焦 刚，胡 雄，曹东海

(北京自动化控制设备研究所， 北京 100074)

0 引言

旋转导向系统是在钻柱旋转钻进时，随钻完成定位与导航的系统，通过实时测量井斜角和方位角等信息对钻头实时定位，并通过接收地面信号完成钻井方向等参数的改变，以达到精确钻井的目的。其中无线随钻测量系统中的往复节流式正脉冲发生器承担信号传输的任务，在下井钻进过程中无法利用电信号传输井斜角、井位深度等测井信息时，可使用泥浆压力脉冲传递信息。在往复节流式正脉冲发生器的设计过程中，提高压力脉冲幅值与信号发生频率是目前研究的热点。国外正脉冲发生器的研究起步于20世纪80年代，经过多次实验迭代,技术已经较为成熟，斯伦贝谢、贝克休斯等油服公司已经掌握了成熟的泥浆脉冲器技术，但相关论文对于正脉冲发生器详细的系统分析鲜有涉及。国内在该领域的起步较晚，目前主流的研究手段为逆向设计，涉及该领域的主流论文大多是基于理想条件下的正脉冲发生器简化模型，得到了计算压力幅值的理论公式，揭示了正脉冲发生器的基本工作原理，但无法应用于复杂的工程实践。

蔡文军等对正脉冲发生器的工作过程进行了仿真分析，通过调整阀体的位置进行多次稳态计算，从而获得阀体位于不同位置时的压力脉冲幅值。房军等针对锥阀式脉冲器信号频率低的问题，提出了往复阀脉冲器模型，通过缩短阀体运动距离提高信号频率。郑宏远等对压力脉冲的传播进行了仿真分析，通过主动控制阀体运动产生脉冲，获得了1000～6000m井深处压力脉冲衰减规律。李红涛基于流体的本构方程以及固体的物性方程，得出了井下压力脉冲衰减系数。岳元龙等基于水锤效应给出了管柱压力波的传播方程，为压力波的传播过程提供了理论分析依据。

需要指出的是，由于脉冲器工作于井下数千米，实际工况复杂，而且脉冲器流道狭长曲折而紧凑，对结构的过度简化、忽略工质的非牛顿特性都会影响数值仿真实验结果。而且脉冲器中主阀体(蘑菇头)与电磁阀的运动与流场耦合，电磁阀堵塞内流道产生的主阀体内外压力差是造成主阀体运动的主要原因，而主阀体的运动又影响流场分布，从而影响电磁阀的运动，最终在流固耦合中达到平衡。

现有涉及正脉冲发生器的论文均使用理想条件下的简化模型，即以阀芯与阀座代替正脉冲发生器的整体结构，利用主阀体步进运动的方式进行稳态数值仿真实验，忽略了最重要的流体与固体的耦合作用。针对上述难点，本文基于前人所做的研究，建立正脉冲发生器的高精度完整流体模型，以及真实工质的物理模型，对正脉冲发生器进行流固耦合瞬态仿真。

综上所述，本文以仿真分析软件Fluent为平台，构建非牛顿流体模型，合理建立部件的运动方程，并基于动网格技术对往复节流式正脉冲发生器进行数值仿真实验，得到限流环直径与入口排量对压力脉冲幅值与信号发生频率的影响。通过分析不同参数下的数值仿真数据，获得了压力脉冲幅值与信号发生频率的变化规律，可应用于工程实践，减少井下实验次数，降低研发迭代成本，提高脉冲器产品的经济性。

1 数值仿真实验建模

1.1 物理模型

往复节流式正脉冲发生器一般由脉冲器、外套筒、主阀杆、主阀体、限流环、滤网等部件组成，右侧为来流方向，如图1所示。

图1 往复节流式正脉冲发生器结构简图Fig.1 Positive pulse generator structure

脉冲器在井下承担信号传输的功能，利用间接水锤原理产生压力脉冲，其基本工作原理为：当电磁阀不通电，内流道流通顺畅时，主阀体腔内压强小于外流道压强，此时主阀体在外流道压力的作用下向下游运动，喉部间隙增大，入口处压力降低，产生一个低压信号；当电磁阀通电，内流道堵塞时，主阀体腔内压强大于外流道压强，此时主阀体在内腔压力的作用下向上游运动，喉部间隙减小，入口处压力升高，产生一个高压信号；待内腔压强与外流道压强相等时，主阀体停止运动。

1.2 边界条件及模型假设

根据实际工作情况，进口处泥浆由恒定体积流量柱塞泵泵入，故模型的入口条件设置为体积流量入口距离滤网300mm,保证湍流充分发展；出口条件设置为表压为零的压力出口，其他均设置为无滑移光滑壁面，如图2所示。湍流模型采用-双方程模型，利用壁面函数法对近壁面流场进行修正。由于Fluent的材料库中没有适用于湍流模型的预定义泥浆模型，因此在本文中选择自定义赫-巴模型，忽略温度对流变参数的影响。泥浆物性方程如下

(1)

式中：为剪切应力，Pa；为剪切速率，1/s。

图2 边界条件示意图Fig.2 Boundary conditions

1.3 流固耦合技术

主阀体由硬质合金材料铸造而成，刚度极高，受流体压力以及黏性力作用时，可忽略受力变形视为刚体。电磁阀维持堵塞内流道所需的电磁力为230N，当内流道压力增加时，电磁阀与内流道连接处将会出现缝隙。由于流场与刚体耦合，且主阀体运动不仅会影响流场分布，同时也会影响电磁阀运动。传统流固耦合技术大多通过流体分析软件与固体分析软件进行数据交换的方法实现，计算量较大，但在考虑刚体变形的情况下有较好的效果。

本文中忽略刚体变形，主阀体与电磁阀运动壁面(图3、图4中粗实线)与变形壁面(图3、图4中粗虚线)如图3和图4所示。仅考虑刚体在流体作用下的运动，故利用用户自定义函数(User Define Function, UDF)功能，使用UDF宏计算刚体所受压力与黏性力的合力，通过离散式(2)的方法列解刚体运动方程，得到刚体运动速度后，使用动网格技术模拟刚体运动对流场分布的影响，从而实现运动部件在流场作用下的被动运动。

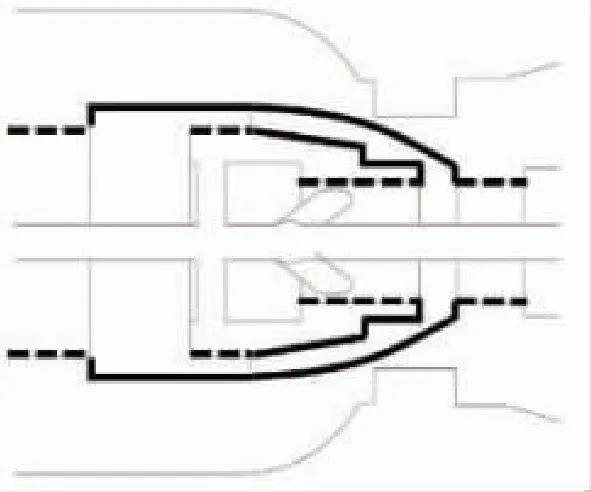
图3 主阀体运动壁面与变形壁面示意图Fig.3 Diagram of valve moving wall and deformed wall

图4 电磁阀运动壁面与变形壁面示意图Fig.4 Diagram of solenoid valve moving wall and deformed wall

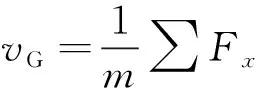
(2)

式中：为刚体质量，kg；为刚体速度，m/s。

=+

(3)

式中：为刚体方向所受合力，N；为刚体方向所受压力,见式(4)，N；为刚体方向所受黏性力，见式(5)，N。

=

(4)

=-STORAGEN3V[0]

(5)

式中：F_P[0]为UDF宏，获取计算面上方向压力，N；F_STORAGE_R_N3V[0]为UDF宏，获取计算面上方向黏性力，N。

整个仿真过程以140ms为一个周期，规定主阀体位于下限位环处时，其坐标为=0；电磁阀位于底座时，其坐标为=0，且上游方向为正向。初始时刻主阀体位于=175处，在内外流道压力差作用下向下游运动；待其平衡后启动电磁阀电磁铁，电磁阀在电磁力与流体压力共同作用下向上游运动直到平衡，此时主阀体在内外流道压力差作用下向上游运动；待其平衡时，一个周期结束。由于实际情况下入口处水泵会产生压力噪音，该噪音的幅值大约为0.1MPa，故当2个时间步之间入口处压力变化小于0.1MPa时，认为刚体运动与流场中各物理量达到平衡状态。

1.4 动网格划分

由于脉冲器流场模型复杂，主阀体与电磁阀运动部分距离壁面较近，流场梯度大，故验证网格无关性是必要的。该数值仿真中,主阀体与电磁阀表面受力是衡量计算精度的重要指标，故本文认为当细化网格后，位于初始位置的主阀体与电磁阀表面受力不再变化时，网格质量达到要求，所得解为网格无关性解。经过多次计算得出，在网格数量为740万时，流场求解达到网格无关性解的要求，下文均采用740万网格模型进行数值仿真计算。

动网格技术广泛应用于阀门开合问题的研究中，模型同时采用网格光顺(Smoothing)与网格重构(Remeshing)两种动网格技术，网格在每个计算时间步完成后进行更新；模型壁面采用变形(Deform)模型，设置变形范围为圆柱体表面，采用本地网格重构因子控制其表面网格重构，防止发生壁面畸变的现象。

动网格技术中的网格重构技术仅可对三角形与四面体网格进行重构，本文利用混合网格技术与计算域分区方法实现了在动网格技术中划分边界层，计算域分区示意图如图5所示。主阀体与电磁阀运动区域划分为全四面体网格，不参与网格重构的其他区域划分为六面体核心网格，如图6所示。

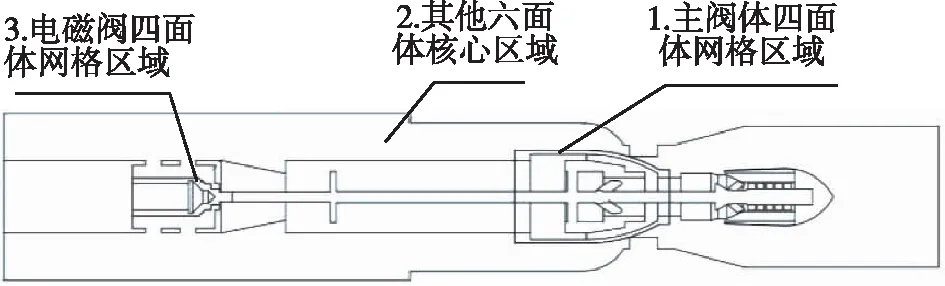
图5 计算域分区示意图Fig.5 Partition of computational domain

图6 流场网格Fig.6 Mesh of fluid

由于主阀体与电磁阀区域(图 5中区域1与3)流场物理量梯度较大，采用局部加密的方法控制面网格与体网格尺寸为均匀0.5mm，其他区域网格尺寸为1～5mm。六面体核心网格数量为229万，四面体网格数量为511万，网格总数为740万。

边界层第一层高度为0.01mm，采用均匀增长的划分方式，壁面+值位于6～50区间，符合工程计算的要求。边界层网格如图7所示。

图7 主阀体与电磁阀边界层网格Fig.7 Prisms mesh

由于四面体网格区域尺寸为0.5mm，故网格重构参数最小重构阈值与最大重构阈值分别为0.4mm与0.6mm，变形表面网格重构采用局部尺寸控制，最小重构阈值与最大重构阈值分别为0.2mm与0.5mm。体网格扭曲率小于0.6，符合数值仿真计算的要求。

1.5 求解算法

压力耦合方程组的半隐式算法(Semi-Implicit Method for Pressure Linked Equations, SIMPLE)于1972年由Patankar等提出，其核心是采用“猜测-修正”的过程，猜测速度场与压力场，利用速度修正方程与压力修正方程修正后完成一次迭代。

随着网格数量的增加以及物理模型的复杂化，分离式求解算法收敛较慢，时常产生数值振荡。故本文中为加快收敛速度，降低解的振荡性，采用Fluent公司和NASA联合开发的压力基耦合算法。该算法对控制方程进行联立求解，时间离散采用多步R-K格式，并采用多重网格加速收敛技术，求解范围从低速流动覆盖到高速流动；同时由于动量方程和连续性方程是紧密耦合求解的，可应用于复杂模型、质量较差网格、时间步长较大的计算。解的收敛效率较SIMPLE类算法有较大提升。

2 数值实验结果及分析

为验证入口排量与限流环内径对往复节流式正脉冲发生器性能的影响，本文进行了八种工况的瞬态数值仿真实验并分析其结果，仿真使用泥浆物理属性如表1所示，工况分类如表2所示。

表1 泥浆物理属性

2.1 仿真设置

数值仿真计算中均采用图2所示流量入口与压力出口，出口压力设置为当地大气压；控制主阀体与电磁阀壁面运动，与运动壁面相邻的变形壁面采用圆柱变形模式；在入口处设置压力监测点,监测不同流量、不同限流环内径与不同流体比重对压力幅值的影响；压力、动量、湍动能与湍流耗散率的离散均采用二阶迎风格式，求解器算法选用耦合算法(Coupled)；调整密度与体积力亚松弛因子为0.5；时间步长取1×10s，计算1400个时间步，物理时间为0.14s。

表2 数值仿真计算工况分类

2.2 限流环内径与入口流量对脉冲器性能影响

第一类～第四类数值实验结果如表3、表5与图8所示，第五类～第八类数值实验结果如表4、表6与图9所示。当限流环内径相同时，随着入口流量的增加，入口处低压、高压值升高，压力波脉冲幅值(压差)升高。当入口排量相同时，随着限流环内径的减小，入口处低压、高压值升高，压力波脉冲幅值(压差)升高。

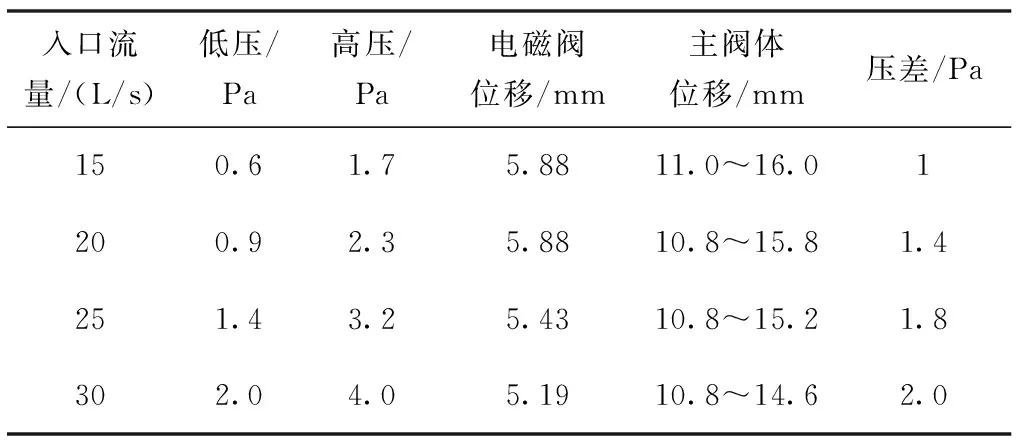
表3 第一类～第四类仿真工况数值实验结果

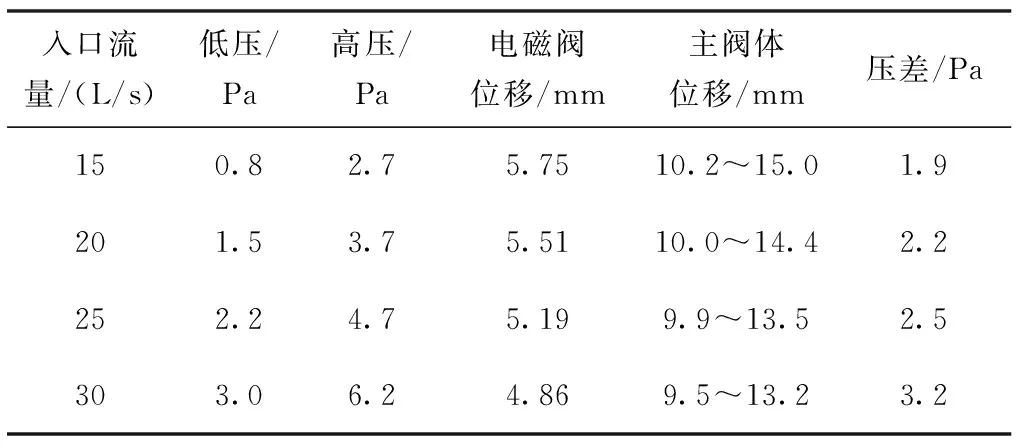
表4 第五类～第八类仿真工况数值实验结果

图8 第一类～第四类仿真工况入口处压力变化曲线Fig.8 Inlet pressure with working conditions No.1～No.4

图9 第五类～第八类仿真工况入口处压力变化曲线Fig.9 Inlet pressure with working conditions No.5～No.8

表5 限流环内径62mm主阀体平衡时间

表6 限流环内径60mm主阀体平衡时间

从图8可以看出，0ms时主阀体位于17.5mm处，随着入口流量的增加，入口处压强也随之升高；25ms时在内外流道压差作用下，主阀体由初始位置第一次运动到平衡位置，时间约为25ms，平衡时间随着入口流量的增加基本保持不变；25ms时电磁阀开始向上游运动，直到其所受流体作用力等于电磁驱动力时停止，随着入口流量的增加，主阀体向上游运动到第二次平衡点的时间减少；85ms时，入口流量为15L/s与20L/s，压力曲线有一段正弦波动，造成波动的原因是随着入口流量降低，电磁阀受流体作用力小于电磁驱动力，内流道完全被堵塞，由于流体的可压缩性，在电磁阀完全关闭的一瞬间，内流道内流体会产生水锤效应，主阀体腔内压力激增，主阀体运动呈现短暂的正弦波规律；130ms时，随着水锤波的耗散，主阀体上受力逐渐趋于平稳，最终达到稳定状态。

从图9可以看出，当使用60mm限流环时没有出现正弦波动，这是由于限流环内径减小，内外流道压强均会升高，导致电磁阀无法完全堵塞内流道，无法激发水锤效应。

对比表5与表6，增加入口排量，主阀体运动一个周期所需的时间减少，即信号发生频率增加；减小限流环内径，主阀体运动一个周期所需的时间减少，即信号发生频率增加。

3 结论

1)数值实验结果表明，在脉冲器结构参数方面，脉冲器限流环的内径与入口流量对压力波脉冲幅值影响显著，限流环内径越小，压力波脉冲幅值越大；入口流量越大，压力波脉冲幅值越大。

2)数值实验结果表明，限流环内径减小或入口排量增加，脉冲器的理论信号发生频率增加。该种型号的无线随钻测量系统的理论最大信号发生频率可达7Hz。但考虑到使用较小内径限流环与较高入口排量将会对供水设备造成较大压力，过高的压力波会对管路系统造成破坏，故工程实践中应当根据实际情况选用合适的限流环与入口排量。

3)对于该种正脉冲发生器，可在正式工程实践前对其建立高精度流体模型，利用动网格与运动控制技术得到特定结构参数下的泥浆脉冲高压、低压、压力幅值与信号发生频率，最终通过调整结构参数使其符合工程实践的要求，降低实验成本。