光纤环非互易相位误差尾纤补偿方法研究
2022-08-05吴雨萌毕聪志孙桂林
吴雨萌,胡 斌,毕聪志,孙桂林,雷 明
(北京自动化控制设备研究所,北京 100074)
0 引言
光纤陀螺是一种基于Sagnac效应的惯性测量组合的核心部件,由于具备无机械运动部件、成本低、寿命长等优点,在诸多领域有着广泛的应用前景。光纤环作为光纤陀螺的核心部件,极易受外部环境的影响,其中,外界温度环境的变化是制约光纤环性能提升和光纤陀螺工程化的主要原因之一,外部温度环境的变化会直接导致光纤陀螺的零位漂移,简称零漂。
零位漂移是衡量光纤陀螺全温性能的重要指标之一,用于评价变温条件下陀螺输出信号平均值的峰-峰值大小。对于光纤环来说,该值越小代表光纤环的温度性能越好。为了改善光纤环温度性能,可以通过合理的热设计来减少外界温度环境对光纤环的影响,还可以通过改变光纤环绕法如增加极数等来减少不对称性带来的非互易相位误差。目前,国内外众多学者已通过改进光纤陀螺结构热设计减少环圈温度梯度,以及通过增加光纤环绕制极数的方式减少光纤环的热致非互易相位误差。此外,近年来,也有学者对于光纤环不对称与光纤环温度特性的关系进行了研究。但光纤环绕制技术复杂,绕制过程难以保证光纤环的完美对称,尤其是缠绕张力波动对内部应力分布影响较大。在不同温度下,应力也会随之发生变化,并且不同光纤陀螺仪的热源分布也不同,因此同一环圈在不同的热源分布条件下产生的热致误差也不相同,这种误差的大小直接影响光纤陀螺的温度性能以及在惯导系统中的应用精度。如何减少光纤环不对称导致的热致误差一直是国内外研究的重点,也是工程应用中的难点。
本文针对光纤环绕制过程中顺逆时针光路不对称带来的非互易相位误差问题,结合实际工程应用需求,在特定设计的光纤环安装结构中,建立光纤环的热互易性仿真模型,计算光纤环尾纤长度非对称对热致误差的影响,并通过变温条件下光纤环温度特性测试完成结果验证,最终得到调整光纤环尾纤长度补偿光纤环非互易相位误差的方法,以提升光纤环实际应用精度和一致性。
1 理论分析
1.1 光纤环热致误差机理
光纤环中不对称的光纤点上有温度扰动时,在环圈中相向传播的两束光将会在不同时间经过这一段光纤,从而产生非互易相移,即Shupe误差。
光纤环的热致非互易相位误差为

(1)
其中,=2π为光在真空中的传播常数;为光在光纤中的传播速度。
将式(1)分为两部分积分:(0,2)和(2,),则可以得到

(2)
式(2)表明,在结构和材料相同的条件下,光纤环上的温度分布、中点左右两侧相同长度位置处光纤的距离,以及起绕点两侧顺逆时针方向光纤长度的差值,均会影响光纤环的热致非互易相位误差。
1.2 光纤环非互易性的原因及补偿原理
目前,光纤环绕制过程中采用了两种方式降低Shupe效应的影响,一是采用对称绕法使得光纤环中点两侧相同长度位置处光纤的距离尽量靠近,从而使得中点两侧光纤受到同样的温度扰动,抵消温度变化引起的误差,在四极对称绕法的基础上,拓展出了八极和十六极绕法、crossover-free 绕法等,以抵消光纤环相邻两个相反方向绕制周期内的相位误差;二是稳定光纤环的缠绕过程,重点是减少张力波动和人为干预,提升光纤环内部的应力稳定性。
由式(1)可知,在光纤环温度条件相同的情况下,影响光纤环热致非互易误差的因素主要在于温度变化导致的光纤长度和光纤折射率的变化。除光纤排布方式外,影响光纤陀螺热致非互易误差的因素还包括:环圈绕制过程中光纤扭曲引起的扭曲应力、环圈胶体固化过程中产生的累积应力,以及光纤环中点不对称导致的顺逆时针方向光纤长度不对称等。这些因素都会直接导致顺逆时针两束光波传输特性发生变化,从而引起光纤陀螺仪相位差的变化。
此外,式(2)描述的是光纤环在理想对称条件下的热致非互易误差,而光纤环在实际绕制过程中并不能保证严格的对称性。实际绕制光纤线圈时,光纤存在中点偏差、光纤直径引起的每层长度不同以及缠绕工艺产生的光纤跃层越匝区等因素,都会导致对称绕法存在非理想性,因此式(2)无法反映中点偏差、光纤直径等因素产生的附加热致非互易相位误差。
假设光纤环中点偏差为Δ,则根据式(2),相对于中点无偏差的光纤环,有中点偏差Δ的光纤环上处实际处于(+Δ)处,因此式(2)变为式(3)
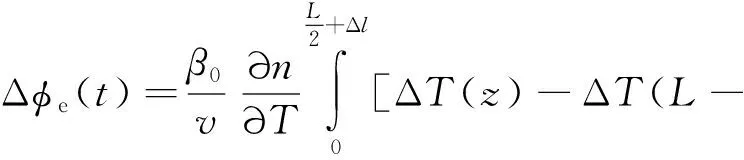
)](2-+2Δ)d
(3)
式(3)表明,光纤环中点偏差或顺逆时针方向光纤长度的差值会改变光纤环的热致非互易误差。因此,可以通过调整光纤环顺逆时针方向光纤的长度,以补偿光纤环中点不对称、光纤扭转的扭曲应力和胶体固化累积应力等导致的光纤环热致非互易误差。
以上所述各种影响光纤环热致非互易误差的因素难以通过理论分析进行定量的研究和计算,因此本文建立光纤环有限元模型,并利用其计算通过截短或延长光纤环不同方向尾纤长度的方式,从而减少因光纤环不对称性导致的非互易相位误差。
2 光纤环仿真分析模型的建立
本文应用的光纤环仿真分析模型为二维固化胶体等效介质模型,光纤环结构参数和仿真模型参数如表1和表2所示。光纤环结构采用交错排布、四极对称绕制方式,共计44层、72匝,环圈内径84mm。仿真分析模型采用二维固化胶体等效介质模型,其中等效介质模型根据等效介质理论计算交错排布方式下光纤环各组分体积分数,得出光纤环等效密度、等效比热容和热传导系数。

表1 光纤环结构参数
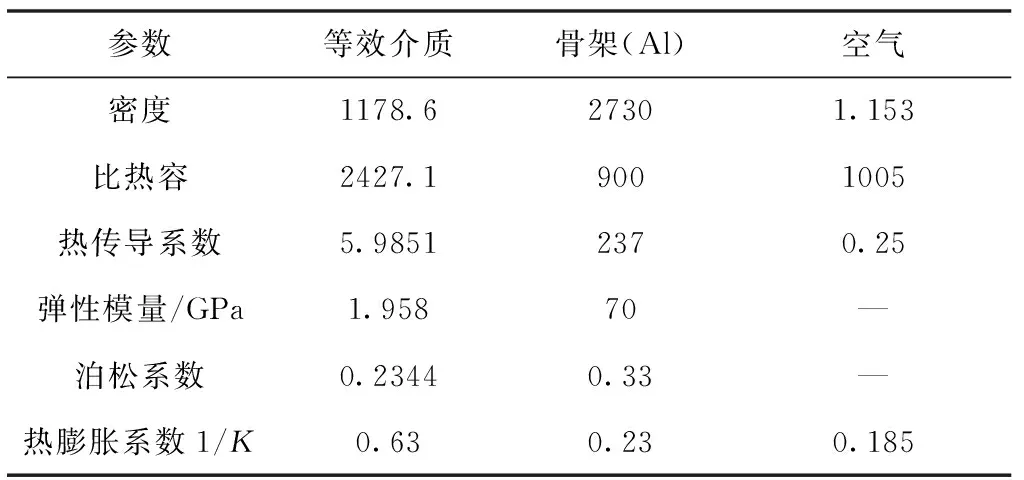
表2 等效介质模型参数
根据实际应用情况,光纤环的温度变化主要来自于空气热对流以及环槽材料热传导,因此根据光纤环热场环境建立热传导介质(环槽)和热对流介质(空气),并通过二维轴对称旋转方式建立光纤环仿真分析模型,环圈周向二维截面如图1所示。 利用Comsol多物理场仿真分析软件,计算出特定温度环境条件下光纤环上各位置处的温度分布场,并将光纤上各点的温度代入离散的光纤环数值模型,具体流程如图2所示,计算得到因光纤环圈变化产生的光纤陀螺仪零位漂移。
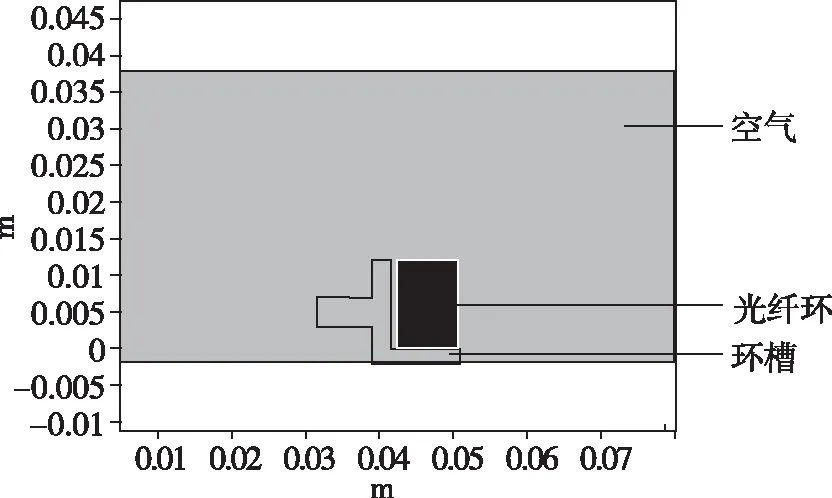
图1 等效模型的二维截面示意图Fig.1 Two dimensional cross section diagram of equivalent model

图2 光纤环仿真分析模型结构Fig.2 Fiber coil simulation analysis model structure
在对尾纤补偿以消除环圈绕制不对称性的仿真分析过程中,光纤环的中点不对称性通过改变环圈第1、2层顺逆时针层数与匝数,并保证环圈层数、匝数的完整对称性来实现;光纤环顺逆时针方向光纤长度的延长或缩短,可以通过增加或减少环圈外侧光纤层数或匝数的方式来实现。
3 仿真分析与实验验证
3.1 仿真结果分析
通过上述仿真分析模型,验证了光纤环中点不对称和顺逆时针方向光纤长度不相等条件下,光纤环输出的热致非互易相位误差。根据上述仿真分析模型建立的光纤环体总长度约为800m,图3所示为仿真分析过程中光纤环加载的温度条件,也是目前光纤陀螺领域通用的应用温度环境。在图3所示温度环境条件下,光纤环在-40℃保温2h后,环圈内部达到热平衡,然后以1℃/min的温变速率升温至+60℃;在+60℃保温2h后,以-1℃/min的温变速率降温至-40℃,并保温2h,完成1个完整的高低温循环过程。
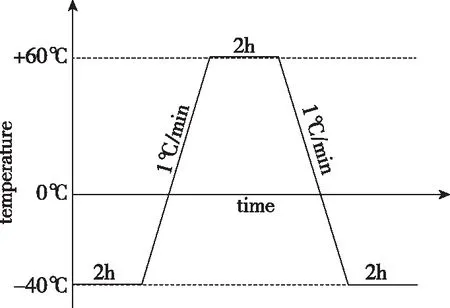
图3 光纤环加载的温度环境Fig.3 Temperature conditions of fiber coil
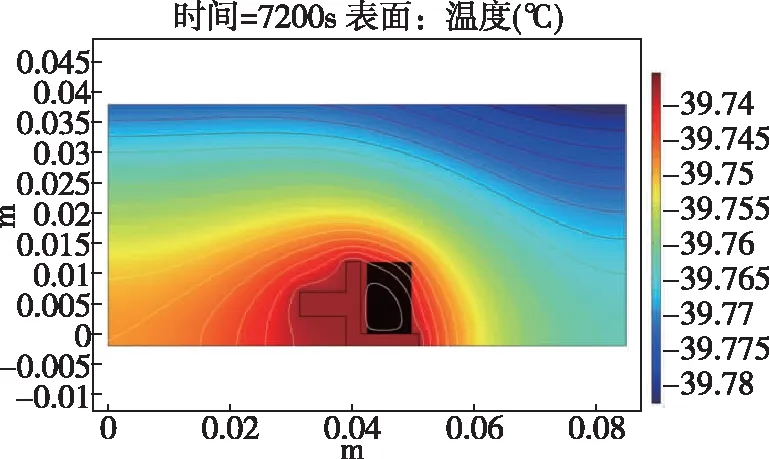
图4 温度加载2h时的温度分布Fig.4 Temperature distribution under temperature load for 2h
对光纤环模型进行温度加载,通过热仿真瞬态分析可以得到各时刻光纤环模型的温度分布情况。图4所示为温度加载2h,即-40℃时光纤环模型的温度分布。由图4可知,当温度降为-40℃并稳定一段时间后,光纤环模型中温度梯度分布情况为光纤环内层温度略高于外层温度。图5所示为温度加载5.5h,即+60℃时光纤环模型的温度分布图。由图5可以看出,当光纤环模型在温度为+60℃的环境中稳定一段时间后,光纤环内层温度要略高于外层温度。
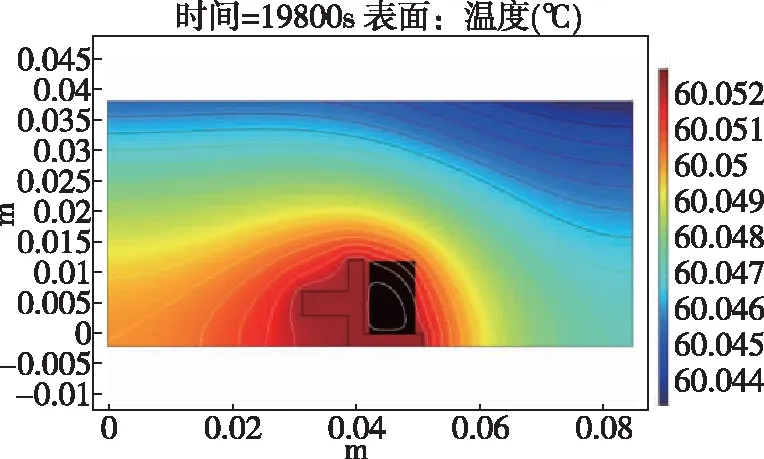
图5 温度加载5.5h时的温度分布Fig.5 Temperature distribution under temperature load for 5.5h
将各时刻光纤环模型上各离散点的温度代入热致非互易误差公式中,即可计算出光纤环的热致非互易误差,并绘制出在图3所示的温度下光纤环热致非互易误差曲线。
在物理上顺逆时针方向光纤长度相等的模型下,将四极对称的光纤环在顺时针方向上截去约0.52m,约2匝光纤,截长前后,光纤环顺逆时针方向的相位差变化如图6所示。从图6中可以看到,尾纤补偿前物理上顺逆时针方向光纤长度相等的模型并不是最优的,顺时针方向的尾纤截长0.52m后,光纤环的热致非互易误差减小。这是由于光程中心与物理上的光纤不重合导致的。因此,需要通过截尾纤来优化光纤环的性能。由图6可知,顺时针方向上截去约0.52m时,截长后环圈热致非互易相位误差的极差减小为原来的43%。
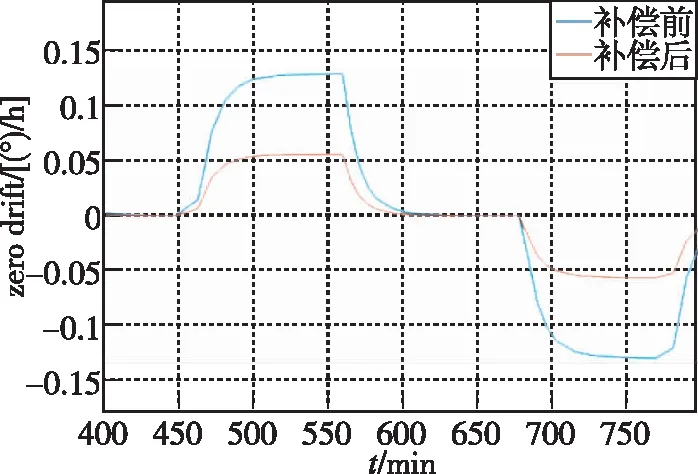
图6 温度变化率为1℃/min时的热致非互易误差Fig.6 Thermally induced nonreciprocal error when temperature rate is 1℃/min
为验证尾纤补偿后,即顺时针方向尾纤截长0.52m时,光纤环在不同变温速率下热致非互易误差变化是否满足同样的规律,在-40℃~+60℃范围内对3℃/min变温速率条件进行了仿真分析。图7所示为3℃/min变温速率下,光纤环完整对称和顺时针方向截长0.52m时的热致非互易相位误差,尾纤调整前后环圈不对称导致的非互易相位误差极差降低至调整前的41%。
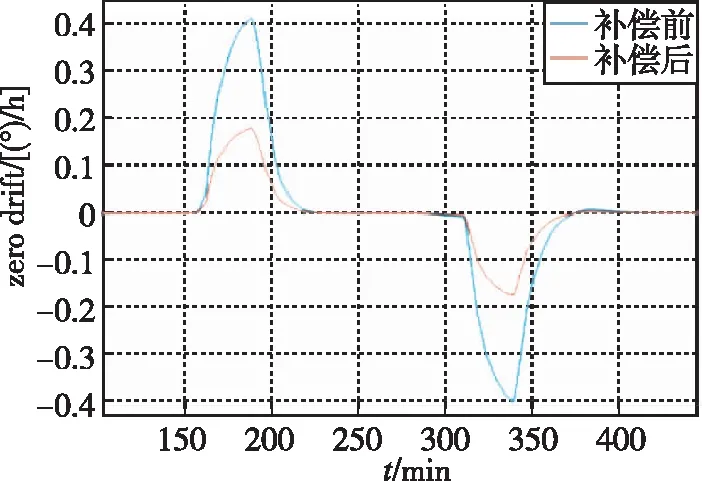
图7 温度变化率为3℃/min时的热致非互易误差Fig.7 Thermally induced nonreciprocal error when temperature rate is 3℃/min
通过以上仿真分析可见,物理结构上完美对称的光纤环不是热致误差最小的状态,通过调整顺逆时针方向的光纤长度可以减小环圈的热致非互易相位误差。对于表1和表2所示结构和材料的光纤环来说,在-40℃~+60℃温度范围和1℃/min以及3℃/min的温变速率条件下,光纤环尾纤长度变化0.52m,可将全温范围内的热致非互易相位误差极差降低至原来的41%。
以上理论及仿真分析均说明,光纤环物理长度的中点不一定是光纤环的光学中点,存在通过调整光纤环环体外尾纤长度以提高光纤环对称性的可能。但是,光纤环中光纤和固定胶应力分布复杂,难以确定缩短或延长的光纤方向,更加难以定量描述缩短或延长的光纤长短。因此,针对设计及工艺定型的光纤环,需要结合仿真分析结果和实验结果,确定光纤环尾纤截长或延长的方向和长度。
3.2 实验结果分析
选用与以上仿真分析结构相同的1#和2#光纤环,进行改变光纤环尾纤长度不对称性以降低光纤陀螺全温零偏的实验。其中,光纤环1#为正常绕制的光纤环,光纤环2#为绕制时出现一些问题的故障环。
实验过程中,为了排除光源、耦合器、Y波导、探测器和数字处理电路对光纤陀螺仪全温零位漂移的影响,图8实线框中的光学器件和电路的配套及装配状态在光纤环顺逆时针尾纤调整过程中均保持不变。
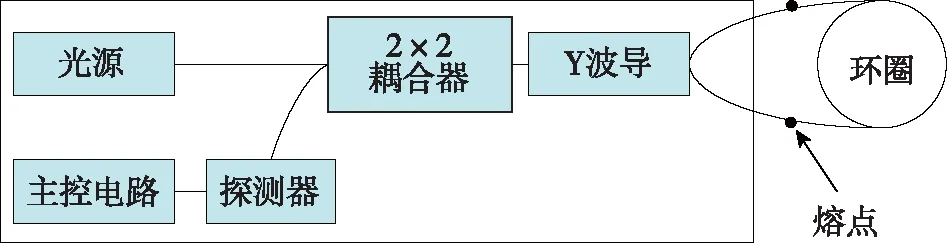
图8 实验光路Fig.8 Experimental light path
表3所示为实验光纤环1#和2#尾纤调整前后相应的光纤陀螺仪全温零位漂移值。

表3 光纤环实验参数及测试结果
图9所示为光纤环1#在1℃/min的温变速率下,顺时针方向尾纤截长约0.46m时,光纤陀螺仪输出零位随温度变化的曲线,尾纤调整前后陀螺仪全温零位漂移值由1.48(°)/h减小为0.87(°)/h。
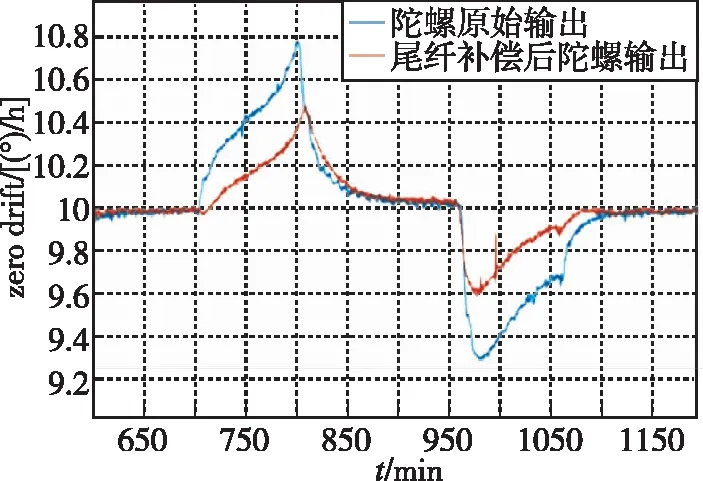
图9 光纤环1#原始输出与逆时针尾纤截去0.5m后陀螺输出曲线Fig.9 Original gyro output and the output after removal of 0.5m fiber in anticlockwise fiber coil
图10所示为将光纤环2#顺时针方向尾纤减少约1.38m时,在一个完整的温度循环内陀螺仪零位漂移值。尾纤调整前后,陀螺仪全温零位漂移值由原来的5.84(°)/h减小为2.30(°)/h。
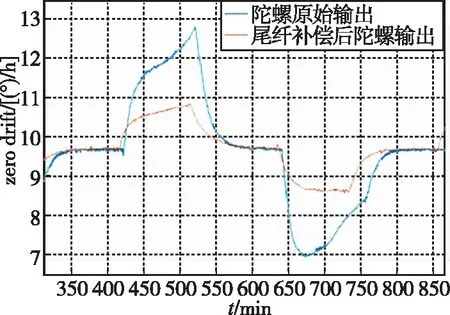
图10 陀螺2#原始输出与逆时针尾纤截去1.5m后陀螺输出曲线Fig.10 Original gyro output and the output after removal of 1.5m fiber in anticlockwise fiber coil
将2个实验环圈配套光纤陀螺仪在3(°)/min温变速率下进行测试,实验结果显示,光纤环1#顺时针尾纤截长0.46m时,对应陀螺仪全温零偏漂移值由3.32(°)/h减小为1.49(°)/h ; 光纤环2#顺时针方向尾纤截长1.38 m时,陀螺仪全温零偏漂移值由7.17(°)/h减小为1.37(°)/h,如图11(a)和(b)所示,其中图11(b)输出异常的点是由于测量过程中温度受到了一次扰动造成的。
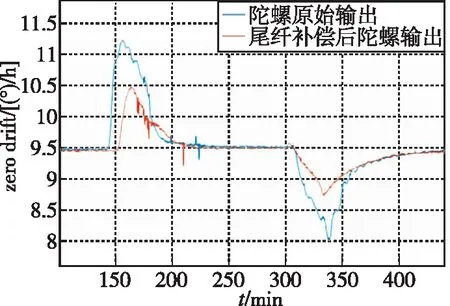
(a) 1#,顺时针截长0.46m

(b) 2#,顺时针截长1.38m图11 实验陀螺仪配套光纤环顺逆时针尾纤不等时陀螺仪全温零位漂移Fig.11 Gyroscope full temperature zero drifts for different length of test tail fiber
通过实验分析,光纤环的零偏漂移偏差可以通过截取光纤环尾纤长度的方式来改善。在实际应用中,针对如1#环圈所示的全温零偏漂移增大的情况,可以在实际生产中,通过将顺逆时针光纤延长或缩短固定长度后,通过有限元仿真分析尾纤截长方向并通过试验结果拟合曲线,寻找最适合长度,从而将光纤陀螺全温零偏漂移降低至最小,以提升光纤环温度性能。针对如2#环圈所示零偏漂移异常增大的情况,可以通过截取尾纤的方式进行补偿,通过调整尾纤长度,尽可能抵消掉光纤环绕制缺陷导致的光纤环零偏漂移异常的现象。
4 结论
本文根据等效介质理论和Mohr理论,建立了光纤环热致相位误差仿真分析模型,并利用该模型分析了不同温度环境条件下,光纤环热致非互易误差与光纤环尾纤长度的关系。文章的结论与不足之处如下:
1)根据光纤环顺逆时针方向光纤长度存在差值时陀螺仪全温零位漂移的变化量,得出了补偿光纤环光程中点偏差的方法及规律。
2)相较于靠实验摸索改变尾纤长度的方法,有限元仿真不仅能够确定截取尾纤的方向,也能得出尾纤长度与光纤环全温零偏漂移的关系,为后续光纤环的全温零位漂移补偿提供了参考。
3)本文的仿真及实验只将零偏漂移曲线的极差作为评判标准,未说明这种方法对陀螺噪声等其他指标是否有关键影响,后续可以围绕其他评判标准开展研究。
