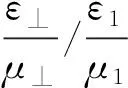单轴各向异性材料的折射性质与全透射研究*
2022-08-03张晓燕吴金随
张晓燕,吴金随
(1. 华北科技学院 理学院,北京 101601; 2. 华北科技学院 安全工程学院,北京 101601)
0 引 言
自然界中物质的宏观性质由物质的介电常数ε和磁导率μ决定[1-2]。对普通的光学材料,ε和μ为正数,称为右手材料[3]。1964年,物理学家Veselago提出电磁波在介电常数与磁导率同时为负的介质中传播是不违反物理学定律的[4-5],并且其具有负折射、旋光性、逆多普勒效应等传统材料所不具备的奇异物理特性。2001年,Smith首次制备出微波段负介电常数和负磁导率材料,并在实验中观察到了负折射现象[6],随后各向异性的人工超材料也被加工出来[7]。由于各向异性材料的介电常数和磁导率在各方向上是不同的,所以能实现更多的电磁特性,具有更广泛的应用,如光子晶体[8]、电磁隐身[9]、波导[10]、偏振转换[11]等。
透射率是光学系统中非常重要的物理量,在倾斜全透射[12]、全反射[13]和超透镜[14]等研究中都有对透射率的分析。本文主要计算了单色平面波在各向异性材料中的色散方程以及波矢量和坡印廷矢量的折射角,在此基础上总结了波矢量和坡印廷矢量的折射性质,通过计算透射率与入射角的关系,得出了全透射条件,进而分析了不同各向异性材料存在透射率和实现全透射需要满足的条件。
1 色散方程
对于各向异性材料,介电常数和磁导率需要用张量形式来表示,选择合适的坐标系可以将张量ε、μ对角化,表示为:
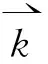
(1)
其满足的麦克斯韦方程为:
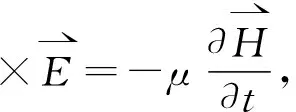
(2)
将式(1)代入式(2)得:
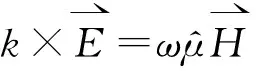
(3)
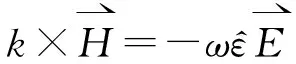
(4)
将(4)代入式(3)得:
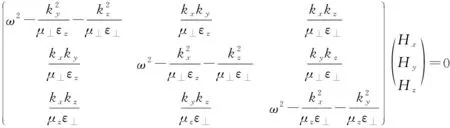
(5)
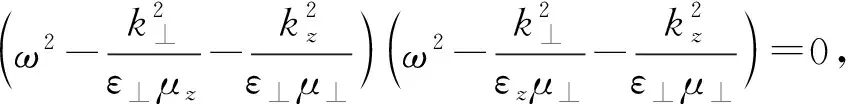
(6)
图1为各向异性材料的色散曲面。从图1可看出,当εzμ⊥>0且ε⊥μ⊥>0时,色散曲面为椭球面;当εzμ⊥>0且ε⊥μ⊥<0时,色散曲面为单双曲面;当εzμ⊥<0且ε⊥μ⊥>0时,色散曲面为双双曲面。TE波与之类似,只要将ε和μ互换即可。
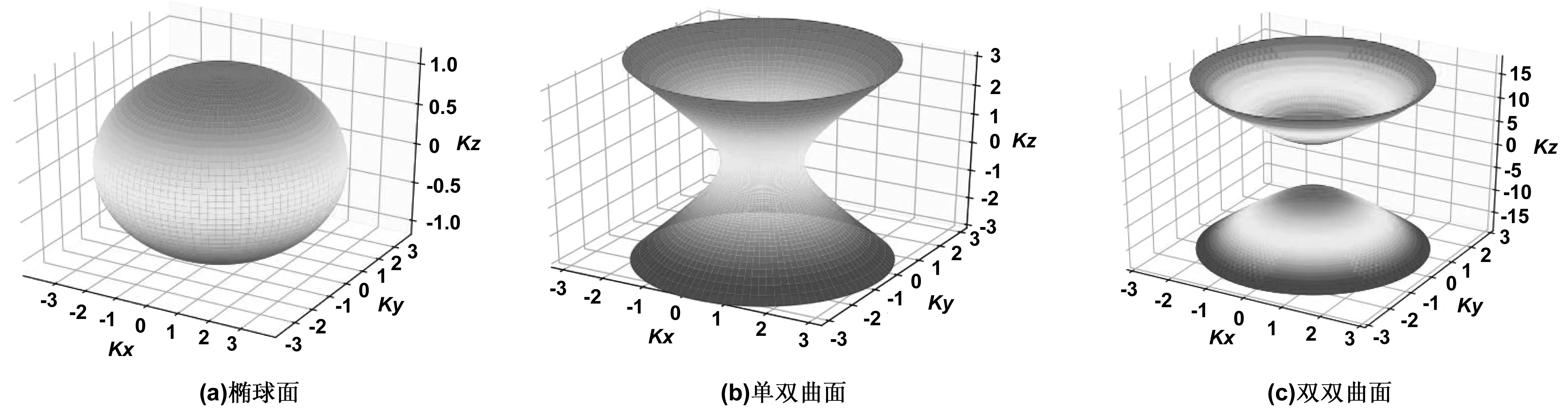
图1 各向异性材料的色散曲面Fig 1 Dispersion surface in anisotropic material
2 各向异性材料中的折射
仍以TM波为例,假设入射方为各向同性右手材料(相关参量下标为1),透射方为各向异性材料(相关参量下标为2),分界面为z=0平面。根据边界条件要求,入射波和折射波在界面方向上的波矢量分量相等(设为k⊥),根据式(6)的结论可以写出入射方和透射方的色散方程为:
(7)
设入射角为θ1、折射角为θ2,则
(8)
将式(8)带入式(7)可以得到折射角与入射角的关系为:
(9)
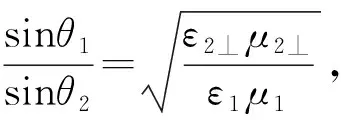
将式(7)带回式(5),可以得到:
(10)
(11)
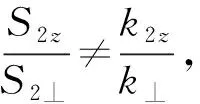
由此可以写出入射方各向同性介质的坡印廷矢量为:
(12)
为保证能量守恒,入射波和折射波的坡印廷矢量在与界面垂直方向上(即z方向)的分量应有相同的符号。对比S1z和S2z,若ε2⊥为正,则k2z和k1z同号,波矢量为正折射,即入射光线和折射光线分居法线两侧;若ε2⊥为负,则k2z和k1z异号,波矢量为负折射,即入射光线和折射光线在法线同侧,这与通常材料的入射光线和折射光线始终在法线两侧的结论不同。
由式(11)和(12)可以得到入射方和折射方的坡印廷矢量与z轴的夹角β为:
(13)
对比可以看出,当波矢量为正折射(即ε2⊥为正,k2z和k1z同号)时,若ε2z为正,则β2和β1符号相同,坡印廷矢量为正折射;若ε2z为负,则β2和β1符号相反,坡印廷矢量为负折射。同理,当波矢量为负折射(即ε2⊥为负,k2z和k1z异号)时,若ε2z为正,则坡印廷矢量为正折射;若ε2z为负,则坡印廷矢量为负折射。这样,ε2⊥的符号体现了波矢量的折射性质,ε2z的符号体现了坡印廷矢量的折射性质。
表1列出了3种各向异性材料在二维情形下(k⊥=kx)的色散曲线以及入射角为45°时波矢量和坡印廷矢量的折射情况,Kz方向表示垂直于界面的法线方向,Kx方向表示平行界面的方向。入射方参数取ε1=μ1=1,透射方参数及对应波矢量和坡印廷矢量的折射角(θ2,β2)列于表中,折射角的符号体现正负折射的性质。由表1可以看出,对椭球曲面材料,波矢量和坡印廷矢量折射性质相同,同时为正折射或负折射;对单双曲面和双双曲面材料,波矢量和坡印廷矢量折射性质相反。
3 各向异性介质中的全透射
仍然以TM波为例进行分析,根据边界条件[15]:
(14)
将式(10)带入可以得到:
(15)
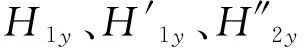
(16)
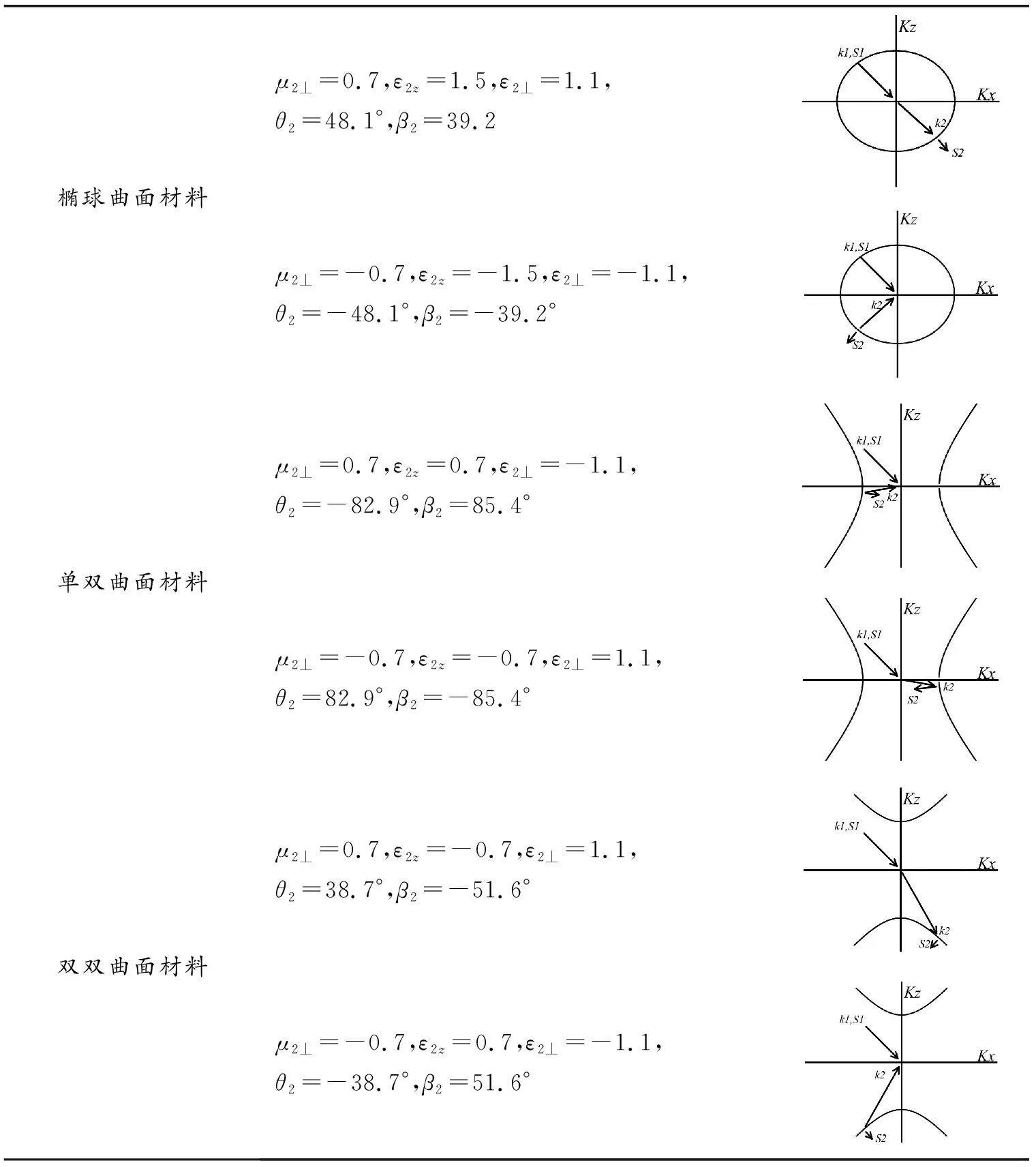
表1 各向异性材料色散曲线及波矢量和坡印廷矢量的折射(ε1=μ1=1,θ1=45°)
将式(8)和(9)带入式(16),可以得到用入射角表示的反射系数和透射系数:
(17)
这也是各向异性介质的菲涅耳定律。反射率和透射率表示为:
(18)
若达到全透射需要T=1,求解得到全透射下的入射角为:
(19)
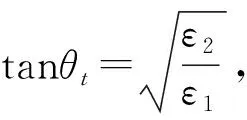
(20)
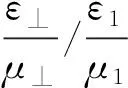
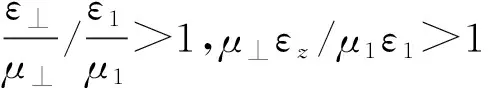
对单双曲面材料,由式(20)可以求得只要满足μ⊥εz/μ1ε1<1就存在全透射角,对应图2(b)中第四象限的阴影区域。在此区域中,当入射角小于θb时不存在折射波,即当入射角大于θb时有透射率,并且存在全透射角。此象限的非阴影区中,透射率为虚数,不会出现折射波。
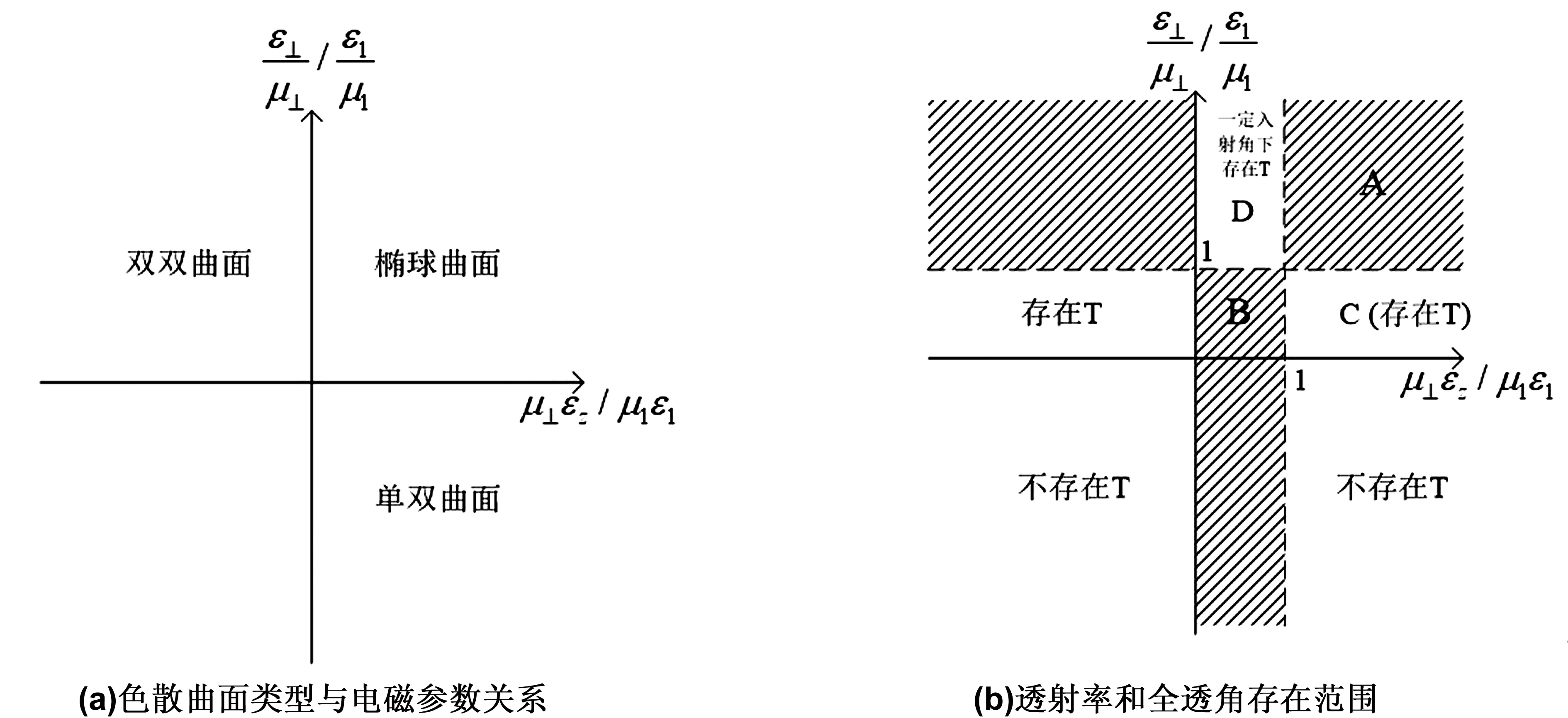
图2 各向异性材料色散曲面类型与电磁参数关系及透射率和全透角存在范围Fig 2 The relationship between the type of dispersion surface and electromagnetic parameters, and the range of transmittance and total transmittance of anisotropic material
对处于第四象限的材料,式(17)始终为虚数,没有传播场,总会发生全反射,不存在透射率。
4 数值模拟
近年兴起的对电磁波调控的方法主要为多重散射机制下的光子晶体和等效介质理论下的超构材料[16-17],下面以由金属-介质微结构实现的超构材料为例数值模拟出现全透射角的范围。金属-介质超构材料由一定厚度的金属、介质薄膜堆叠而成,金属、介质层的厚度都远小于入射光波长[18]。根据有效介质理论,金属介质多层膜可以从宏观上用有效介电常数表征[19]:
(21)
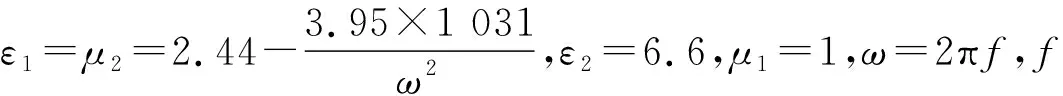
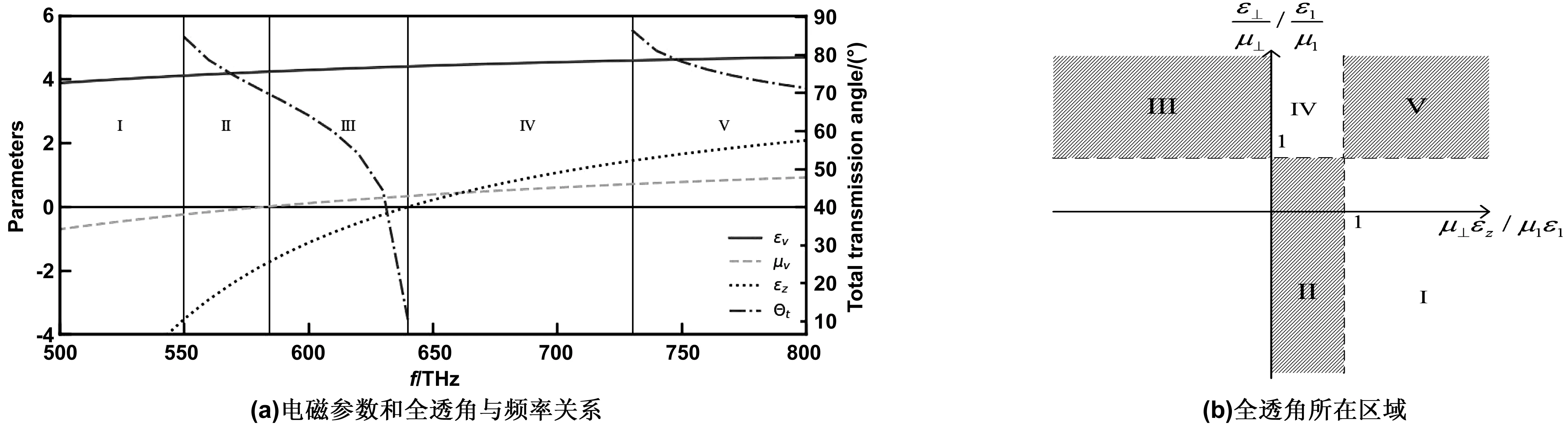
图3 金属-介质超构材料对3种各向异性材料的实现及存在全透角范围Fig 3 Realization for three kinds of anisotropic materials by metal-dielectric multilayer structure and existence of total transmittance angle range
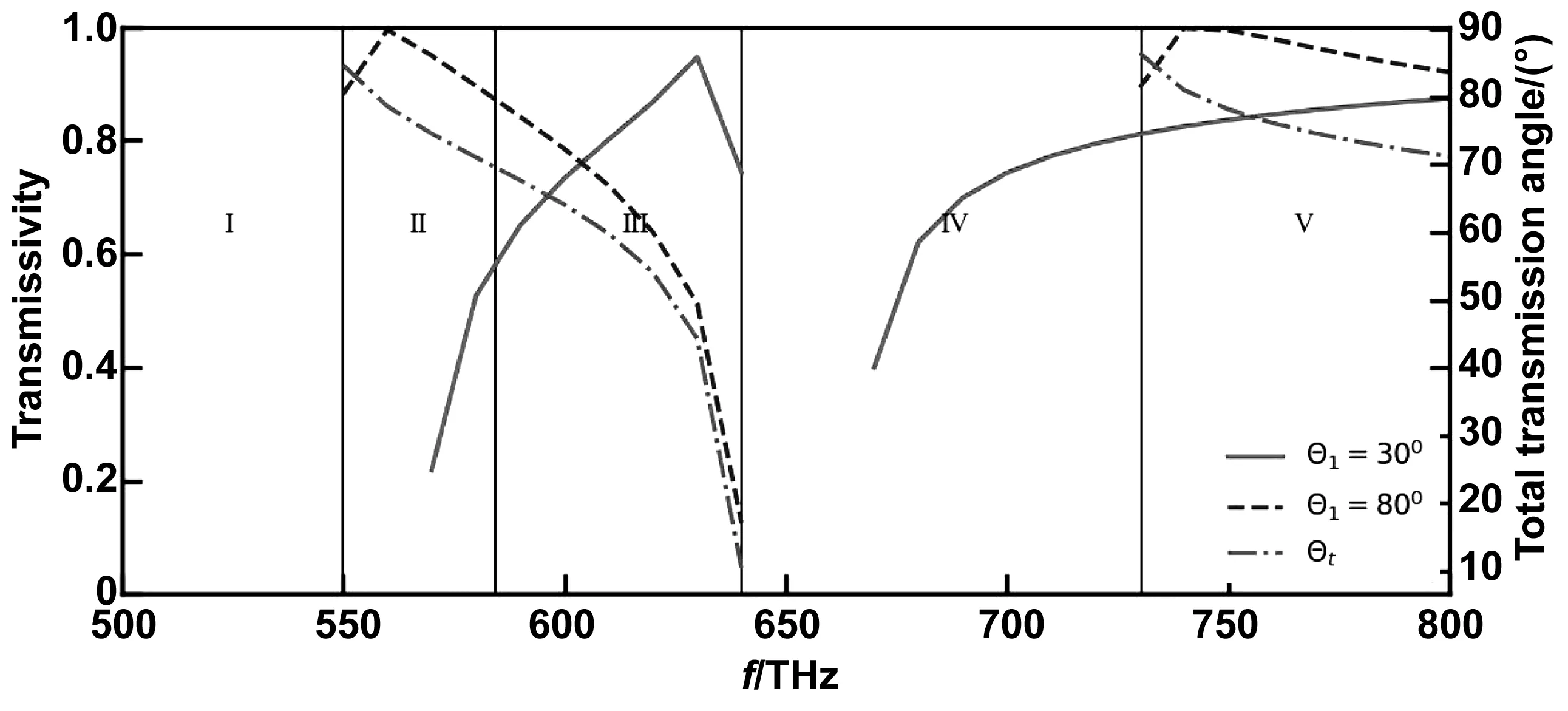
图4 3种各向异性材料的透射率和全透角随频率变化关系Fig 4 The relationship between transmissivity, total transmittance angle and frequency of three kinds of anisotropic materials
图4描绘了在30°和80°入射情况下透射率与频率的关系,为方便比对,依旧保留了全透角曲线。从图4可以看到,I区域在任何入射角下都不存在透射率,Ⅲ和Ⅴ区域在任何入射角下都有透射率。II区域频率范围为550~584 MHz,计算得临界角θb从68°降到12°,570 MHz对应临界角为30°,80°入射时因为入射角始终大于临界角,所以整个区间都存在透射率;而30°入射时,在550~570 MHz范围内因入射角小于临界角,不存在透射率,在570~584 MHz才出现透射率。IV区域属于椭球面材料,需要入射角小于θb时才存在透射率,计算得到整个区间临界角在17~70°之间,670 MHz对应临界角为30°,所以80°入射下没有透射率,而30°入射下在频率大于670 MHz之后出现透射率。透射率出现的范围与前面给出的结论是一致的。由此可知,当材料的厚度比变化时,各类型材料存在的频率范围会有变化,全透角的范围也会相应变化,但并不违背各类型材料出现透射率和全透角的参数条件。
5 结 论