基于循环相关的加权分数阶傅里叶变换信号旋转因子估计方法

张笑宇， 宋碧雪， 王洋， 冯永新， 钱博

(1.沈阳理工大学 信息科学与工程学院， 辽宁 沈阳 110159；2.山东特种工业集团有限公司 军品研究所， 山东 淄博 255200；3.长春理工大学 电子信息工程学院， 吉林 长春 130022)

0 引言

电磁频谱域由于资源有限成为继海陆空天后各国竞争的又一大战备域，为赢得未来战争中的信息主动权，美军针对信息化战场的复杂电磁环境提出了电磁战替代电子战的信息对抗思路。作为一种电磁频谱利用率高的新型通信手段，加权分数阶傅里叶变换(WFRFT)因实现简单，得到普遍的关注和认可。随着通信物理意义的明确，不仅具有单载波系统抗多普勒能力，同时兼顾多载波系统抗多径能力的WFRFT在保密通信领域得到更多研究者的重视。考虑到混合载波体制在未来信息对抗中的抗截获和抗识别优势，对WFRFT信号开展精确的关键参数估计，对现代通信对抗有至关重要的意义。

作为一种新型调制信号，WFRFT信号的研究主要集中在正向通信系统的参数优化及其性能分析上，文献[2]针对当前多参数(MP)-WFRFT星座特征缺乏定量研究的不足，提出一种新型的星座叠加方法，该方法以星座模糊及裂变为依据，构建了基于MP-WFRFT的星座预编码相关混合整数优化模型。文献[3]为提高卫星通信系统的性能，提出一种基于的通信系统预编码设计方法，该方法分析了MP-WFRFT星座的变化规律，构建了基于MP-WFRFT的星座预编码优化系统。文献[4]为解决卫星通信信号隐蔽性不足的问题，提出一种基于MP-WFRFT的通信方法，该方法通过将信号伪装成其他调制方式，增强卫星通信信号的隐蔽性。

针对WFRFT信号的识别和参数估计问题研究较少，文献[5]提出一种WFRFT信号参数识别方法，该方法在分析典型WFRFT信号特征和抗扫描特性的基础上，已知调制方式下通过高阶累积量估计WFRFT信号的旋转因子；未知调制方式下通过扫描法和判决法估计WFRFT信号的旋转因子，并利用神经网络对提出的参数估计方法进行了进一步优化。

循环相关法利用相关函数和功率谱密度互为傅里叶变换对的基本思想，通过循环相关代替传统线性相关的信号处理方法。相对于传统的线性相关信号分析法，循环相关采用圆周相关中快速傅里叶变换(FFT)算法降低乘法运算的复杂度，从而缩短参数估计的时间。

本文将循环相关法引入WFRFT信号旋转因子估计中，提出一种基于循环相关的WFRFT信号旋转因子估计的方法，以实现未知信号参数条件下的旋转因子估计。

1 WFRFT通信机理及其信号特性分析

1.1 通信机理

WFRFT在通信中的物理意义可理解为：信息数据经过串并转换后分别进入4个支路进行处理，其中3支路和4支路的数据在加权处理之前都经过了离散傅里叶变换(DFT)模块，刚好对应于以正交频分多路复用(OFDM)为代表的多载波通信模型，1支路和2支路的数据没有经过DFT模块，则对应于单载波的通信模型。受4个支路的影响，WFRFT是一种同时具有单载波和多载波的混合载波通信模型。

基于上述思想，WFRFT通信模型原理框图如图1所示。在发射端中，将基带信号经过串并转换处理后生成待调制的信号；然后输入旋转因子，生成加权因子信号，并对生成的待调制的信号进行WFRFT调制并添加循环前缀；最后经过并串转换、D/A转换及上变频，得到WFRFT信号，并通过天线发射。

图1 WFRFT通信模型原理框图Fig.1 Functional block diagram of the WFRFT transmitter

在接收端中，利用天线接收经过信道的带高斯白噪声的WFRFT信号；其次，对接收信号进行下变频、A/D转换、串并转换及移除循环前缀；然后，经过傅里叶变换和频域均衡后，接收方进行WFRFT逆变换，再经过串并转换后即可解调原始信号。

基于WFRFT的通信模型产生的信号由于同时包含了单载波及多载波两种调制类型，产生了一种单、多载波调制信号特征过渡的信号形式。因此，作为传统时、频域通信信号的延伸，WFRFT通信信号兼顾时、频通信信号的优势和特点。WFRFT通信信号中单、多载波占比由加权因子决定，即旋转因子为0时，WFRFT的通信模型等价于传统单载波通信模型；当旋转因子为1时，WFRFT的通信模型等价于以OFDM为代表的多载波通信模型。

1.2 信号产生及特性分析

作为经典傅里叶变换的周期性分数化扩展形式，4项加权分数阶傅里叶变换(4-WFRFT)的表达式为

()=WFRFT((),())=
()+[()]+{[()]}+
{[(())]}

(1)

式中：WFRFT(·)表示信号的加权分数阶傅里叶变换；()为原始信号，为信号的采样时间；为旋转因子；(·)表示信号的傅里叶变换；(=0,1,2,3)表示加权因子，

(2)

这种变换域信号可理解为区间[0，4)范围内变化旋转因子在时域和频域的加权叠加，且旋转因子表现为如下特点：当旋转因子趋近于0或2时，时域占比增加；当旋转因子趋近于1或3时，频域占比增加，若旋转因子为0，则第1个加权系数为1、其他系数为0，此时WFRFT等价于原始时域信号；若旋转因子为1，则第2个加权系数为1、其他系数为0，此时WFRFT等价于信号的传统傅里叶变换。

传统离散傅里叶变换如(3)式所示。

(3)

式中：()为信号的频域量，为频域采样点；()为时域分量，为时域采样点；为信号长度。

为描述简洁，将离散傅里叶变换(DFT)和离散傅里叶逆变换(IDFT)改写为矩阵形式如(4)式所示：

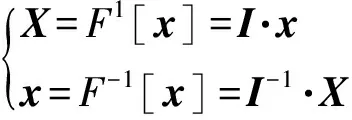
(4)

式中：和为DFT和IDFT运算；离散傅里叶矩阵如(5)式所示：

(5)

因此，矩阵形式的离散化WFRFT如(6)式所示：

(6)

=()+()+()+()=
()+()+()·+()··

(7)

式中：、、为第1次、第2次、第3次DFT运算。

由DFT的周期性和置换矩阵的特性可知，时域反转分量()是()的反转操作，二者的关系如(8)式所示：

(8)

4-WFRFT可利用反转模块和DFT模块实现，其实现原理如图2所示。

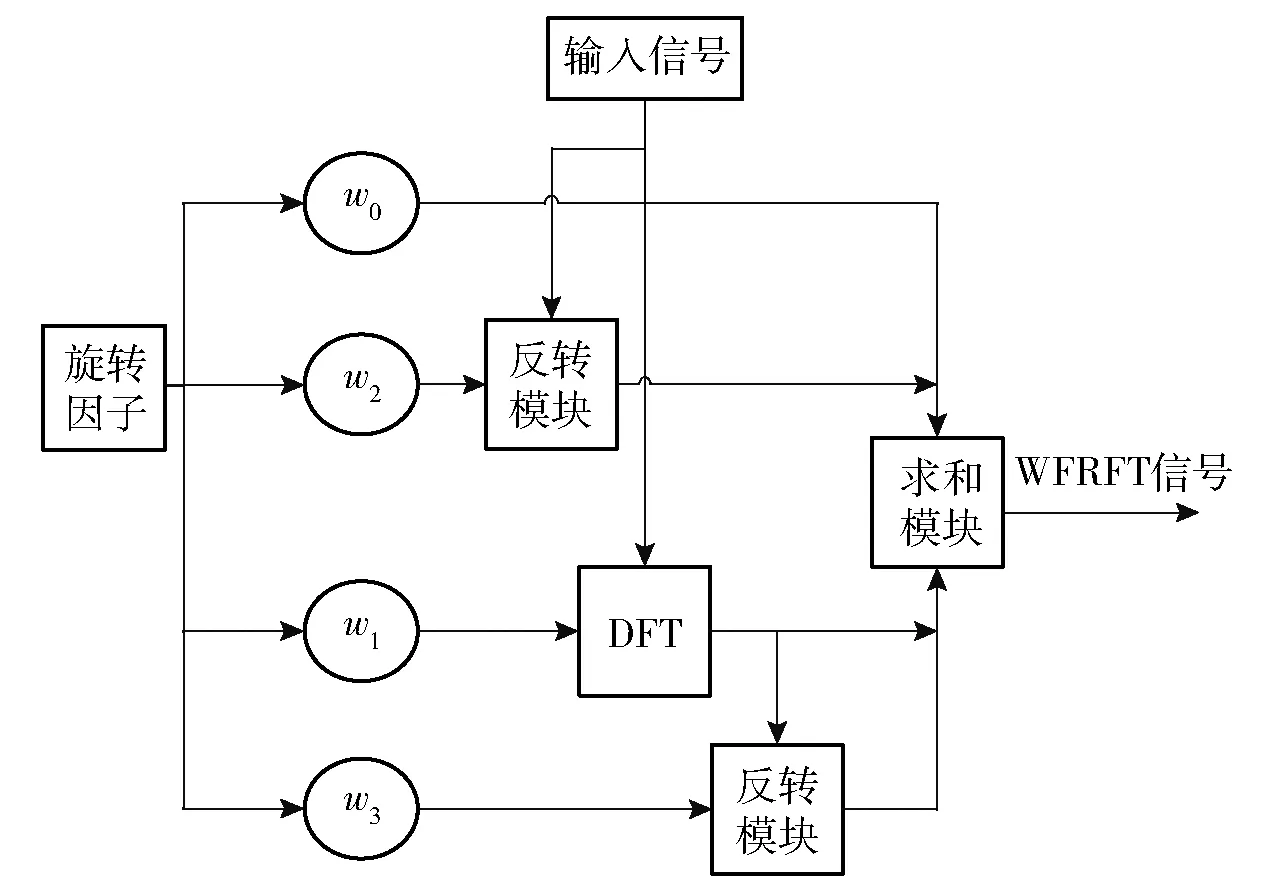
图2 WFRFT实现原理图Fig.2 Schematic diagram of WFRFT

由于WFRFT具有和OFDM相同类型的输入信号，二者区别仅为WFRFT改变了信号在时频域的信号特征。WFRFT信号的特性分析可通过多电平的载波调制方法实现，以正交相移键控(QPSK)、正交幅度调制(QAM)等传统调制方式为基础，对同相支路分量和正交支路分量分别进行WFRFT运算，即可完成WFRFT调制，进而分析WFRFT的信号特征。

图3为QSPK及WFRFT功率谱图对比。由图3可以看出：WFRFT信号的功率谱密度和QPSK信号的功率谱密度基本相同，两种系统具有基本相同的均峰功率比，射频部分的设计基本相同，因此可兼容于现有通信系统；单载波信号、多载波信号及WFRFT混合载波信号具有相同水平的频谱利用率。

图3 QSPK及WFRFT功率谱图对比Fig.3 Comparison of the spectrum of original QPSK and WFRFT signals

WFRFT的功率谱密度可表示为

(9)

式中：为输入信号的方差；为采样周期；(·)为传递函数；为频率；为输入信号的均值；为采样点数。WFRFT的功率谱密度由连续谱和离散谱两部分共同组成。

图4为不同旋转因子下WFRFT信号星座图描述，描绘了WFRFT多变的信号特征。由图4可见，随着WFRFT中旋转因子的变化，WFRFT信号的星座点在QPSK星座点的基础上逐渐分裂、旋转，且在不同的旋转因子下呈现不同的信号特征。

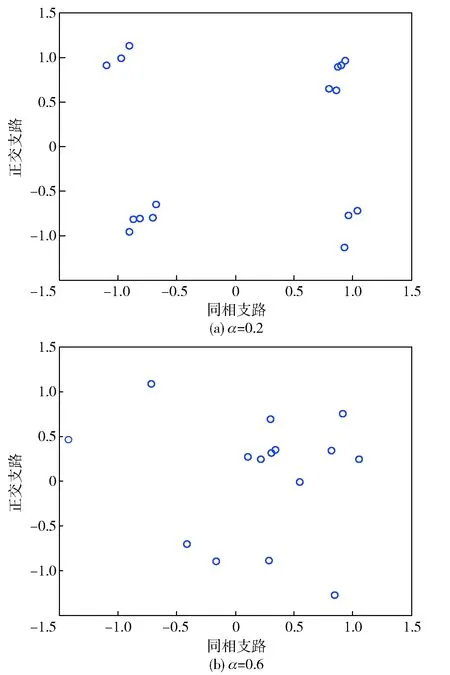
图4 WFRFT调制星座图对比Fig.4 Comparison of constellation diagrams of the WFRFT signals

这是因为WFRFT信号的星座特征同时受到原信号的时域信号特征、频域信号特征以及加权因子的共同影响，各自作用如下：

1)时域分量()与时域反转分量()的加权叠加使得WFRFT信号星座分布径向改变，即以QPSK星座图中每一个星座点为中心产生一簇和输入信号同分布的星座点。

2)频域分量()与频域反转分量()的加权叠加使得WFRFT信号星座分布逐渐高斯化，且WFRFT信号星座图和QPSK信号具有相类似的星座分布。

3)加权因子决定了WFRFT中各分量对信号特征的贡献程度。通过控制加权因子可实现WFRFT在复平面的信号表征形式，决定复平面图形相应的伸缩程度及偏转趋势。其中，WFRFT各信号分量受加权因子影响产生的相位偏转为

(10)

式中：为相位偏转；为旋转因子序列。

2 循环相关机理及复杂度分析

循环相关法最早应用于扩频信号的快速同步捕获中。传统的线性相关可定义为2个采样点数均为的信号进行重叠的信号部分移位相乘累加的过程，其信号长度为2-1。两段采样点数不同的信号线性相关表达式为

(11)

式中：()为采样长度的接收信号；()为接收信号的共轭。由于线性相关等价于信号翻褶后与另一个信号进行移位相乘再求和的过程，与卷积运算相似，只是卷积和没有翻褶，此时线性相关可表示为

(12)

线性相关中的加法次数为2-1，乘法次数为，因此要想提高运算速度，需从减少移位相乘求和的运算量，特别是乘法运算的开销。

由傅里叶变换理论可知，时域上的卷积可用频域相乘实现，此傅里叶变换对可表示为

()=(+)·()

(13)

式中：为经过DFT后的频域值；(+)、()分别为(+)和()对应的频域分量。此时计算(+)与()的相关函数只需做一次IDFT即可。通过分析可知，对于短信号，传统的线性相关运算速度较快，但对于长信号，采用DFT和IDFT计算相关可极大提高运算速度。

WFRFT信号的自相关函数()可表示为

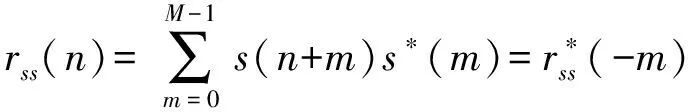
(14)

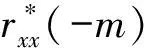
与线性相关相比，循环相关过程为WFRFT信号的圆周相关求解，由于采用了圆周相关中快速FFT算法，其计算速度可以大大提高，从而实现快速计算过程。采用基于FFT的循环相关计算WFRFT的相关值，运算长度仅为线性相关信号长度的一半。

(15)

通过此比值，即可衡量线性相关和循环相关法在旋转因子估计的复杂度性能。

3 循环相关法旋转因子估计流程

由于WFRFT具备良好的相关性，即相同旋转因子的WFRFT自相关性好，而不同旋转因子的互相关性很差。因此，利用WFRFT的相关性对WFRFT信号的旋转因子进行估计。

不同于扩频通信中的接收方本地信号，WFRFT接收方中的本地信号是指对接收信号分别进行旋转因子为[0，4]的WFRFT变换而产生的信号。根据WFRFT自相关性和周期性，当旋转因子分别为0、4以及发送端的旋转因子时，接收信号和本地信号的相关性将会出现峰值。

为缩短估计时间，采用循环相关法进行旋转因子的估计，循环相关估计旋转因子的原理框图如图5所示，该方法共采用2次FFT和1次IFFT计算相关函数。通过循环相关，根据(16)式分别计算旋转因子[0，4]的本地信号和接收信号的相关函数，获取每个旋转因子下的相关函数的最大峰值，计算旋转因子除0和4外的最大峰值所在的位置。

={[((()),
((WFRFT{(),})))]}

(16)

式中：为最大峰值位置；(·)为最大值所在位置；(·)为取最大值；()为接收信号；(·)为取共轭；为接收方本地信号的旋转因子值。

由于WFRFT具有周期性，通过最大值所在位置与已知旋转因子可有效估计未知的旋转因子值，待估计的旋转因子与最大值所在的位置如(17)式所示。

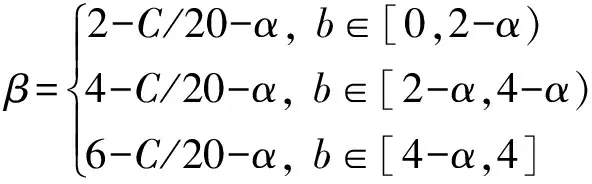
(17)

基于循环相关的旋转因子估计原理如图5所示，旋转因子的估计过程可分为以下4个步骤：

图5 基于循环相关的旋转因子估计原理框图Fig.5 Estimation functional block diagram of cyclic correlation

求点输入信号的FFT和本地信号的FFT。

求输入信号FFT和本地信号FFT共轭的乘积，并求乘积的IFFT。

求每个旋转因子下的相关函数的最大峰值，求旋转因子除0和4外的最大峰值所在的位置。

根据峰值最大位置估计出旋转因子。

4 仿真与分析

为验证提出方法的可行性和正确性，用MATLAB软件对WFRFT信号旋转因子估计性能进行验证与分析。具体仿真参数如下：调制方式为QPSK，载波振幅1 V；载波频率51.25 MHz；采样频率1.025 GHz；信息码周期200 ns；初始旋转因子为0.3；信道为高斯白噪声信道。

首先，对利用相关性估计WFRFT信号旋转因子的可行性进行仿真验证，归一化相关值结果如图6所示。

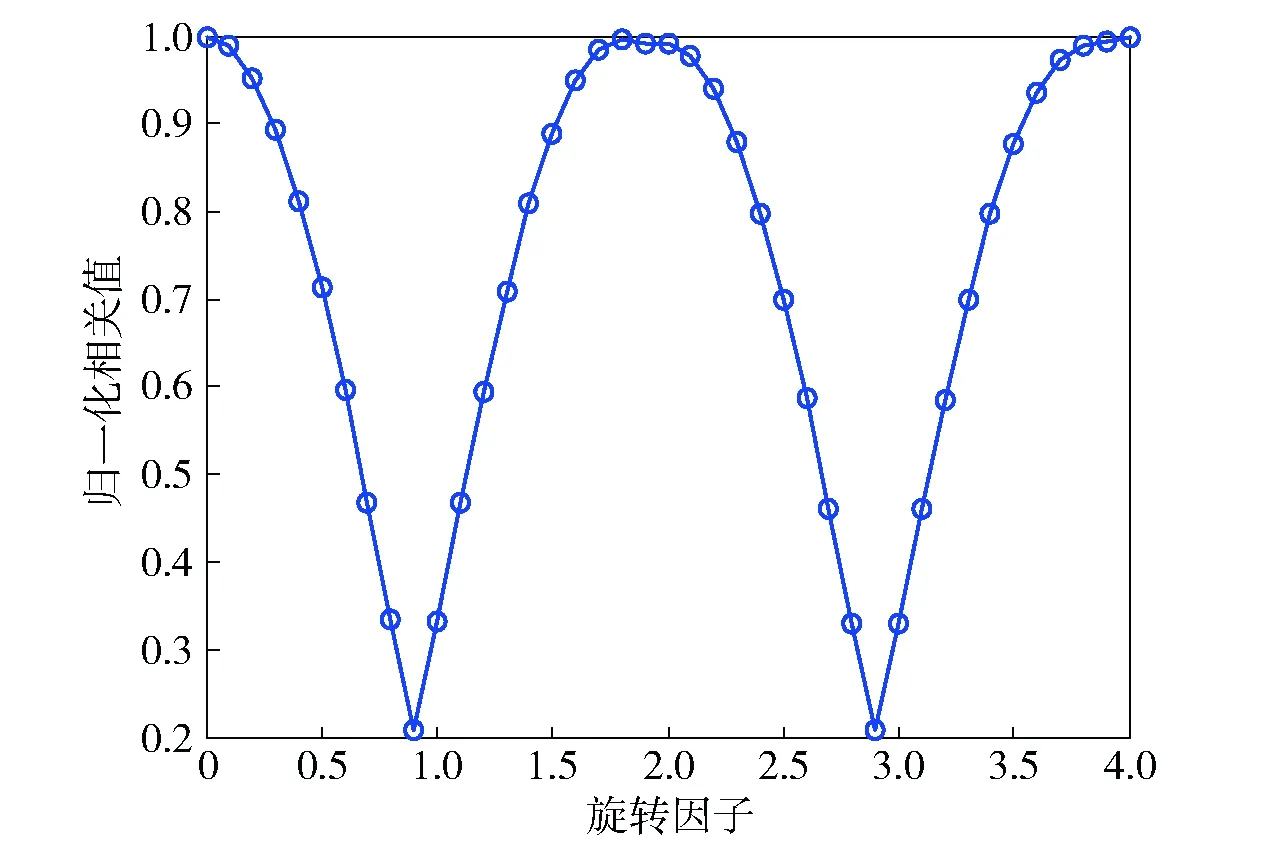
图6 不同旋转因子WFRFT归一化相关值Fig.6 Normalized correlation value of different rotation factors of weighted fractional fourier transform

由图6可见，WFRFT信号的相关函数出现了3个峰值，分别是在旋转因子为0、2、4处。这是因为WFRFT信号具有周期性，即对WFRFT信号再次进行WFRFT的信号仍为WFRFT，且信号的相关性不受影响。除去自相关函数出现峰值外，当本地的旋转因子与接收信号的旋转因子相同时，同样会出现峰值。根据WFRFT的周期性，[1，3]和[3，5]的自相关峰值相同，即WFRFT进行循环相关后同样呈现周期性的变化规律，且变化周期为2，上述归一化自相关峰值搜索范围可进一步优化为[1，3]，此区间内有且只有1个峰值。

采用循环相关计算旋转因子[1，3]的相关函数的最大峰值，最大峰值所在的位置如图7所示。由图7中可知，在不同旋转因子下，循环相关法相关最大值所在的位置呈分段式周期性变化规律，且最大值所在的位置与已知的旋转因子有关系。在旋转因子为[0，1.7)的区间内，最大值所在的位置在区间[0，34)上直线下降；在旋转因子为[1.7，3.7)的区间内，最大值所在的位置在区间[0，38)上直线下降；在旋转因子为[3.7，4]的区间内，最大值所在的位置在区间[34，38]上直线下降。

图7 循环相关法相关最大值所在位置图Fig.7 Position of the maximum correlation value of cyclic correlation

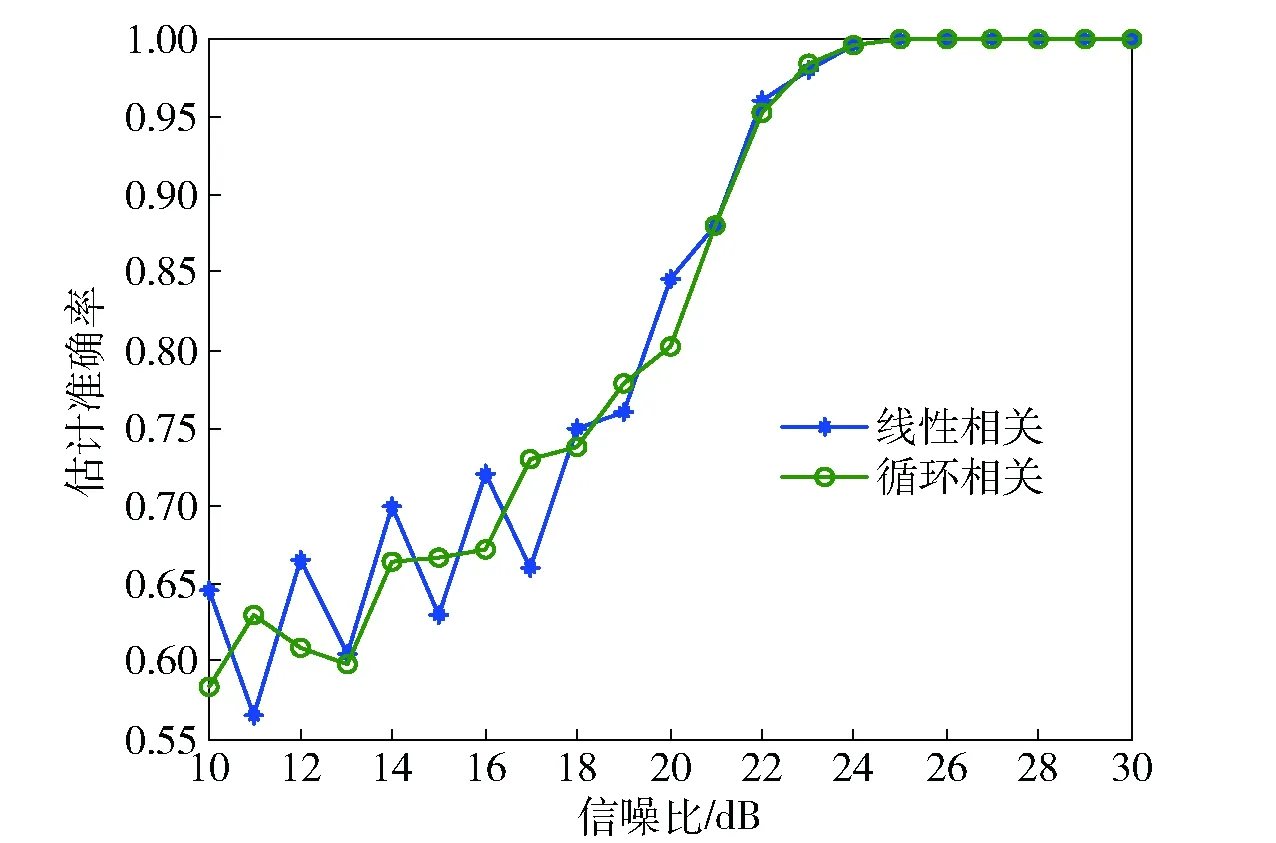
图8 线性相关和循环相关法旋转因子估计准确率对比Fig.8 Comparison of rotation factor estimation accuracy between linear correlation and cyclic correlation

由图8可知：当信噪比大于22 dB时，WFRFT的相关性受到噪声的影响小，相关峰值容易被捕获，此时循环相关法估计的旋转因子准确率接近100%；随着信噪比的减小，当信噪比小于22 dB时，WFRFT的相关性受到噪声的影响变大，WFRFT的相关峰值被淹没在噪声中，此时循环相关法估计的旋转因子准确率开始下降。

图9 线性相关和循环相关法运算时间对比Fig.9 Comparison of computation time for linear correlation and cyclic correlation

不同信号处理长度下，信噪比为10 dB，线性相关法和循环相关法计算时间对比结果如图9所示。由图9可知，当信号处理长度大于64时，由于所需的乘法运算复杂度越低，循环相关相比于传统线性相关的计算时间优势较大。但信号处理长度的增加会增大硬件设计的要求，此时需要根据WFRFT信号的特性，采用如均值法和分块搜索法的处理手段和方法，并通过合理地设置每一次循环相关的长度，优化循环相关的结果。

为验证不同采样时间下基于循环相关法的旋转因子估计性能，信号处理长度分别为512、1 024和2 048个采样点的估计准确率对比结果如图10所示。由图10可知，基于循环相关的加权分数阶傅里叶变换信号旋转因子估计性能与信噪比和采样长度均有关，采样长度越大算法的估计性能越好。这是由于采样长度越大，处理数据点数越多，WFRFT信号的自相关性越好。因此在实际的参数估计过程中应在处理能力范围内，尽可能增大采样长度来提高估计性能。

图10 循环相关不同采样长度估计准确率对比Fig.10 Estimation accuracy comparison of the cyclic correlation at different sampling lengths

为进一步验证不同待估旋转因子的循环相关法估计性能，图11给出了信号处理长度为512个采样点，待估旋转因子分别为0.1、0.3和0.5在10～30 dB条件下的旋转因子估计准确率变化曲线。由图11可以看出，不同旋转因子下的估计性能相当，表明循环相关的估计方法与参数选取无关，可以适用于不同旋转因子参数下的WFRFT信号。

图11 循环相关不同旋转因子估计准确率对比Fig.11 Estimation accuracy comparison of rotation factors of cyclic correlation under different rotation factors

为进一步验证本文提出的旋转因子估计性能，图12给出了信号处理长度为512个采样点，循环相关法和文献[5]中的高阶累积量法()在10～30 dB条件下的旋转因子估计准确率变化曲线。由图12可以看出，本文方法的估计准确率优于文献[5]中的高阶累积量方法，尤其在信噪比为10～15 dB的条件下；高阶累积量法中信噪比需24 dB才可达到100%的估计准确率，相对于高阶累计量法，在估计准确率为100%时可提高2 dB的估计性能。

图12 循环相关和高阶累积量旋转因子估计准确率对比Fig.12 Estimation accuracy comparison of rotation factors of cyclic correlation and higher order cumulates (HOC)

5 结论

1)在分析WFRFT信号及其特性的基础上，通过统计分析不同旋转因子归一化相关值的峰值及其位置，实现WFRFT信号的旋转因子估计。为缩短参数估计的时间，利用循环相关代替传统线性相关，采用圆周相关中快速FFT算法降低乘法运算的复杂度，提出了一种基于循环相关的WFRFT信号旋转因子估计方法。通过设置合理仿真参数，在不同参数条件下进行参数估计性能的验证。

2)仿真结果表明，基于循环相关的参数估计方法可有效地估计WFRFT信号旋转因子，且有效缩短旋转因子估计的时间，为WFRFT通信对抗提供重要的依据。

[1] 吴佳隆，任清华，李明. 基于MP-WFRFT的物理层保密增强安全方案[J].信号处理，2021，37(4): 528-535.

WU J L，REN Q H，LI M. A physical layer security enhancement scheme based on MP-WFRFT[J]. Signal Processing, 2021, 37(4): 528-535. (in Chinese)

[2] WU J L，REN Q H，LI M. Research on physical layer encryption scheme of tactical network based on WFRFT[J]. Journal of Physics: Conference Series，2020，1549(2):71-78.

[3] 吴佳隆，任清华，李明. 基于CR-WFRFT的物理层安全认证方法[J].空军工程大学学报(自然科学版)，2020，21(3):93-98.

WU J L，REN Q H，LI M. A physical layer security authentication method based on CR-WFRFT[J].Journal of Air Force Engineering University (Nature Science Edition)，2020，21(3): 93-98. (in Chinese)

[4] GAO W B，LI B Z. Convolution theorem involving n-dimensional windowed fractional Fourier transform[J]. Science China (Information Sciences), 2021, 64(6): 169302.

[5] 杨振鑫.WFRFT信号参数识别方法研究[D].哈尔滨: 哈尔滨工业大学，2020.

YANG Z X. Studies on the methods of parameters identification of WFRFT signal[D]. Harbin: Harbin Institute of Technology，2020.(in Chinese)

[6] 费顺超.低空网络化弹药高效地空直扩通信技术研究[D]. 沈阳:沈阳理工大学，2018.

FEI S C. Research on the technology of high-efficiency ground-to-air direct sequence spread spectrum communication for low-altitude Networked ammunition[D]. Shenyang: Shenyang Ligong University，2018. (in Chinese)

[7] 翟东，达新宇，梁源. WFRFT-MIMO卫星抗截获通信系统[J].空军工程大学学报(自然科学版)，2018，19(2):26-32.

ZHAI D，DA X Y，LIANG Y. Satellite anti-interception communication system with WFRFT and MIMO[J].Journal of Air Force Engineering University (Nature Science Edition)，2018，19(2):26-32. (in Chinese)

[8] 张笑宇，冯永新.一种基于时分数据调制的加权分数阶傅里叶变换通信方法[J].兵工学报，2020，41(7):1360-1367.

ZHANG X Y，FENG Y X. A communication method based on time division modulation weighted fractional fourier transform[J]. Acta Armamentarii, 2020, 41(7): 1360-1367. (in Chinese)

[9] 张笑宇.面向网络化弹药的多域调制二维信息传输关键技术研究[D].沈阳: 沈阳理工大学，2021: 47-54.

ZHANG X Y. Research on key technology of 2-Dimension information transmission for multi-domain modulation orient networked ammunition[D]. Shenyang: Shenyang Ligong University, 2021: 47-54. (in Chinese)

[10] LIU F，WANG L，XIE J，et al. MP-WFRFT and chaotic scrambling aided directional modulation technique for physical layer security enhancement[J]. IEEE Access，2019, 7: 74459-74470.

[11] LIANG Y, DA X Y, XU R Y, et al. Research on constellation-splitting criterion in multiple parameters WFRFT modulations[J]. IEEE Access, 2018, 2018(6): 34354-34363.

[12] LIANG Y, XIANG X, SUN Y, et al. Novel modulation recognition for WFRFT-based system using 4th-order cumulants[J]. IEEE Access, 2019, 7: 86018-86025.

[13] WANG X L，MEI L，WANG Z D，et al. On the probability density function of the real and imaginary parts in WFRFT signals[J].China Communications，2016，2016(9): 44-52.

[14] WANG Z D，MEI L，SHA X J. BER analysis of WFRFT precoded OFDM and GFDM waveforms with an integer time offset[J].IEEE Transactions on Vehicular Technology，2018, 67: 9097-9111.

[15] WANG Z D，MEI L，SHA X J. BER analysis of STBC hybrid carrier system based on WFRFT with frequency domain equalization[J]. Science China, 2018, 61(1): 082301(1)-082301(13).

[16] WANG Z D，MEI L，WANG X L. On the performance of hybrid carrier system based on WFRFT with power allocation[J]. IEEE Access，2018，6: 29231-29240.

[17] FANG X J，SHA X J，MEI L. Guaranteeing wireless communication secrecy via a WFRFT-based cooperative system[J]. China Communications，2015，2015(9):76-89.

[18] SHA X J. Hybrid carrier CDMA communication system based on weighted-type fractional Fourier transform[J]. IEEE Communications Letters，2012，16(4): 432-435.

[19] FANG X J, SHA X J, LI Y. Secret communication using parallel combinatory spreading WFRFT[J]. IEEE Communications Letters, 2015, 19(1):31-33.

[20] WANG Z D，MEI L，WANG X L. BER analysis of hybrid carrier system based on WFRFT with carrier frequency offset[J]. Electronics Letters, 2015, 51(21): 1708-1709.