大气层外弹道导弹中段拦截弹道规划

赵蒙， 端军红， 王明宇， 殷双斌

(1.空军工程大学 防空反导学院， 陕西 西安 710051； 2.93792部队， 河北 廊坊 065000)

0 引言

弹道导弹具有射程远、速度快、精度高、威力大、突防能力强等特点，如何对来袭弹道导弹实施有效拦截一直是各军事强国防空能力建设的重点。2018年随着美俄相继退出《中导条约》，反弹道导弹(简称反导)再次成为世界各国关注的热点问题之一。弹道导弹中段拦截又称中段反导，一般是指对处于飞行中段的弹道导弹进行拦截摧毁，其拦截过程如图1所示。中段反导作战涉及的关键技术非常多，但拦截弹道规划是中段反导作战制导、控制拦截弹飞行的前提和依据，国内外有关于空间轨道目标拦截问题的文献资料相对较多，对于非机动变轨的弹道导弹目标，相对于空基武器而言，使用地基拦截弹对目标实施拦截是一种快捷、有效而且技术复杂度相对较低的方法，但是目前有关于地基拦截弹道规划的文献资料相对较少。

本文利用椭圆弹道理论对目标飞行轨迹进行预测，在获得遭遇点的位置后，依据拦截弹发射点位置和拦截弹飞行时间，基于Lambert方程建立拦截弹飞行弹道规划模型，并对拦截弹规划模型的有效性进行仿真验证。该模型为中段反导拦截弹道规划设计提供一种思路和方法，若拦截弹符合所规划的拦截弹道在发射能量、飞行时间、拦截高度、飞行程序设计等约束条件的要求，理论上可满足中段反导拦截作战要求，能够实现对目标的拦截。

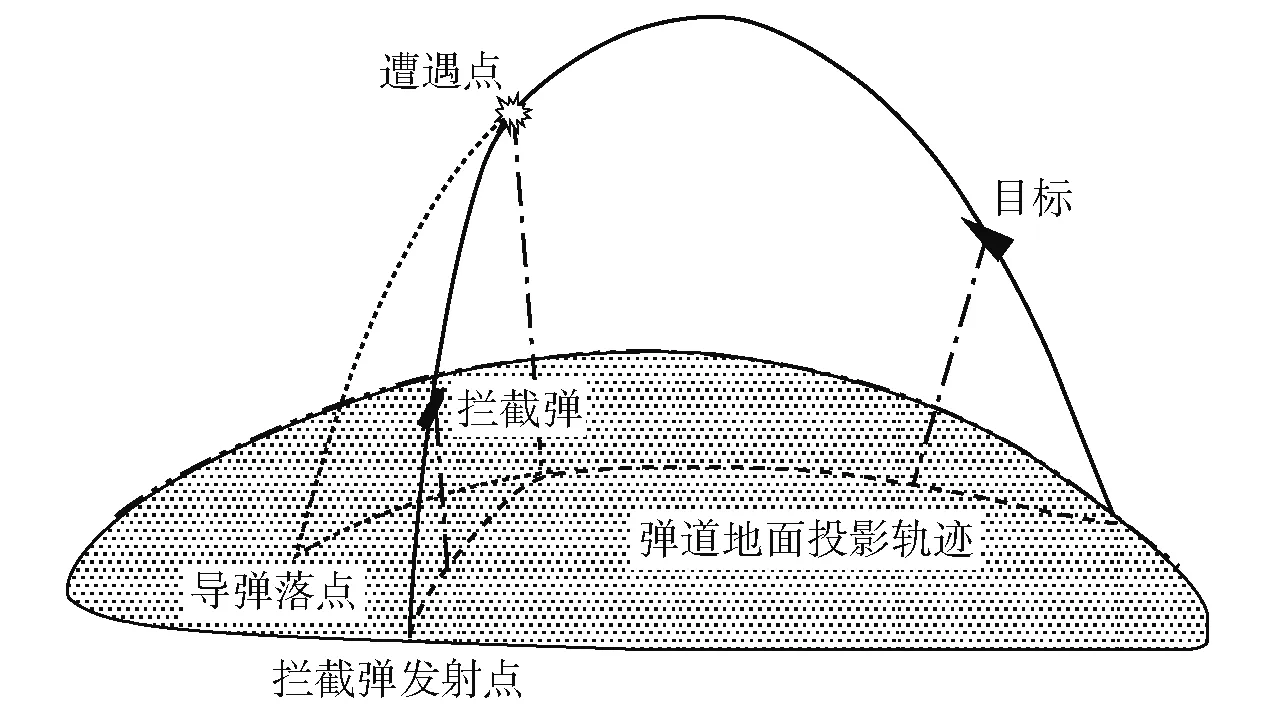
图1 反导拦截过程示意图Fig.1 Schematic diagram of anti-missile interception

1 遭遇点预测模型

1.1 坐标系定义

在建立目标与拦截弹的遭遇点以及拦截弹弹道规划模型中，主要涉及的坐标系有地心惯性坐标系、地心固定坐标系、站心坐标系以及大地坐标系，相关坐标系的定义以及各个坐标系之间的转换在文献[2]中都有详细描述和转换公式。本文后续模型建立过程中如不特殊说明，所有计算都在地心惯性坐标系下进行。

在大地坐标系下，假设预警探测系统探测到弹道导弹发动机关机后，时刻某一点的位置坐标为(,,)、速度矢量为(1,2,3)。通过坐标变换可得地心惯性坐标系下弹道导弹的位置矢量=(，，)和速度矢量=(，，)。

则弹道目标在点的极径、速度以及速度矢量与当地水平面间的夹角的大小分别为

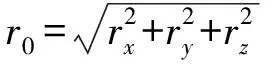
(1)

(2)

(3)

1.2 椭圆弹道参数

弹道导弹的飞行弹道按照发动机的工作状态，可分主动段和被动段两大部分。根据弹道导弹飞行过程中受力的不同，被动段又可分为在大气层以外的自由飞行段和进入大气层后的再入飞行段。其中在自由飞行段由于弹道导弹始终处于大气层以外飞行，可认为导弹只受到地心引力的影响，则弹道导弹与地球就构成一个二体系统，其飞行轨迹近似为以地心为焦点的椭圆轨道。

弹道导弹目标自由飞行段的弹道方程为

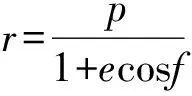
(4)

式中：为地心矢径的模；为椭圆弹道的半通径；为椭圆弹道的偏心率；为椭圆弹道的真近点角。

由目标状态矢量、可得椭圆轨道的半通径、偏心率及椭圆半长轴具体计算公式如下：

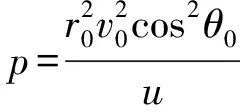
(5)

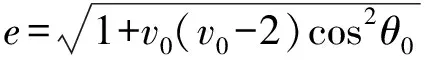
(6)

(7)

式中：=，为万有引力常数，为地球质量。

则时刻目标在点的真近点角和偏近地点角，可由(8)式、(9)式唯一确定：

(8)

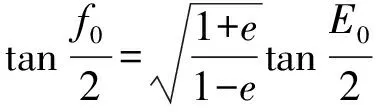
(9)

式中：2与2总是处于同一象限内。

1.3 目标轨迹预测

根据二体理论，时刻后直至弹道导弹再入大气层这段时间内，弹道导弹目标任意时刻的位置矢量可由椭圆轨道方程解算。设经过Δ=-后，时刻的偏近点角为，则可利用牛顿迭代法求解下式获得：

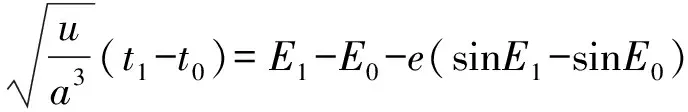
(10)

则时刻目标在点的位置矢量=(1,1,1)、速度矢量=(1,1,1)预测模型为

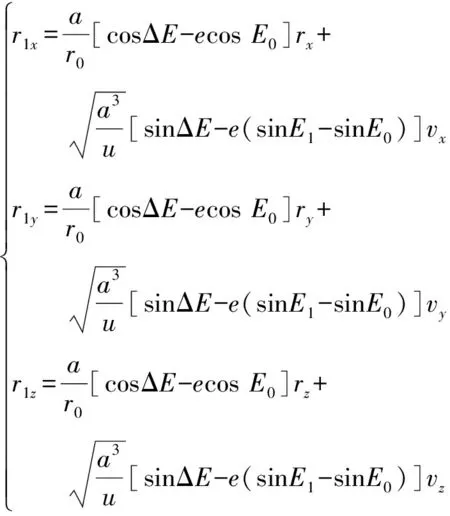
(11)

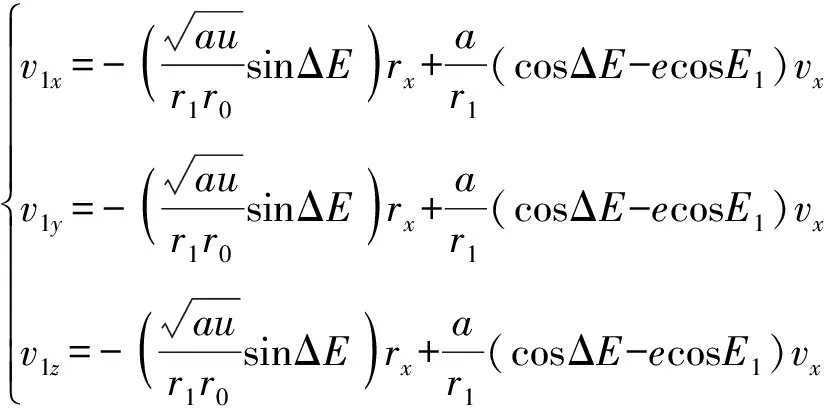
(12)

式中：Δ=-。

2 拦截弹道规划模型

2.1 问题描述

中段拦截武器系统的拦截弹飞行过程与弹道导弹基本类似。拦截弹的弹道按照发动机工作状态可分为主动段和被动段。主动段主要依靠发动机提供的推力按照程序飞行，在拦截弹发动机关机后就进入被动飞行段，若不考虑中段制导控制情况下，其后续弹道飞行轨迹完全由主动段结束时刻拦截弹的位置矢量和速度矢量所决定。拦截弹在主动段的受力情况非常复杂，直接建模非常困难，根据反导拦截弹主动段的飞行程序，应用弹道方程可比较容易获取拦截弹在主动段结束时刻的运动状态参数，为了简化建模的复杂性，在被动段近似认为拦截弹的轨迹为以地心为焦点的椭圆弹道，从而将复杂的弹道规划问题转化为经典的Lambert问题进行处理。

拦截弹弹道规划的Lambert问题描述是：已知拦截弹发射点的位置矢量=(2,2,2)、遭遇点的位置矢量=(3,3,3)以及拦截弹的飞行时间，规划一条椭圆半长轴为、偏心率为、半通径为的椭圆轨道，实现拦截弹在时刻从点发射，时刻与目标在点遭遇。完成弹道规划计算后，则可解得拦截弹发射后的位置矢量和速度矢量，根据拦截弹发动机关机点高度，利用(13)式可求得拦截弹发动机关机点的真近点角为

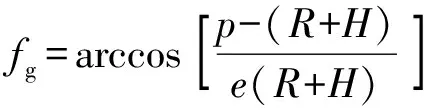
(13)

式中：为地球赤道半径大小。

将(13)式代入(8)式、(9)式，可得偏近点角以及拦截弹从发射后至发动机关机点的飞行时间Δ，最终可求解得到拦截弹在发动机关机点处的位置矢量和速度矢量。求解出、后，则可通过工程方法设计出拦截弹的主动段飞行程序。

2.2 弹道规划模型

根据上述描述，在已知、情况下，实质上只要求出拦截弹发射点或者遭遇点处的速度矢量(2,2,2)、(3,3,3)问题即可解决。根据Lambert定理，引入普适变量，从而建立飞行时间与的函数关系，根据文献[18]，拦截弹的径向速度满足

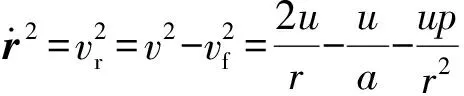
(14)

式中：为径向速度；为周向速度。

定义满足

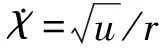
(15)

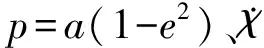
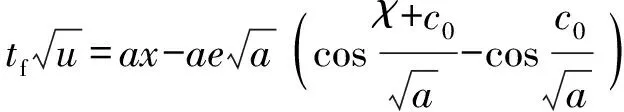
(16)

式中：为积分常数。

令=，则飞行时间的普适公式可表示为

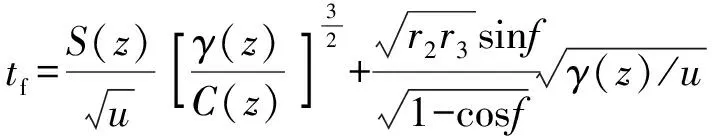
(17)

式中：

(18)

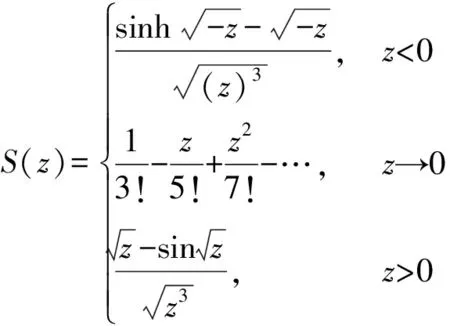
(19)

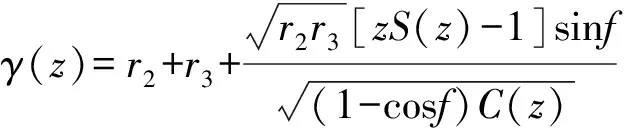
(20)

利用、()和()表示的拉格朗日系数和分别为

(21)

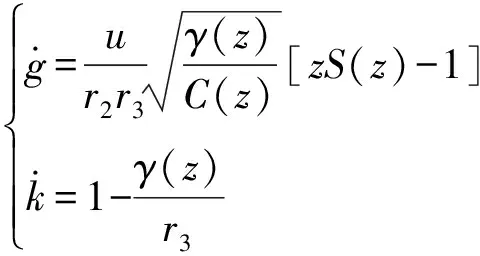
(22)

(23)

式中：Δ表示两点真近点角之差，Δ=-；·=23+23+23。

为求出的值，建立函数

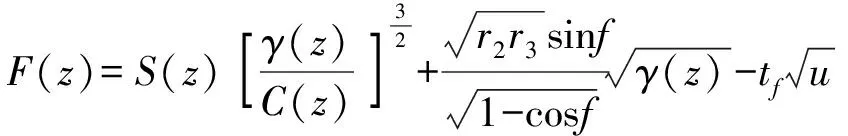
(24)

将代入(24)式中，通过牛顿迭代法可最终求出的值，将求得的值代入拉格朗日系数中，由此可得出与为

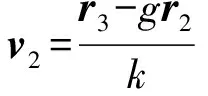
(25)

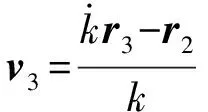
(26)

再利用(4)式～(12)式即可得到拦截弹发射后的位置矢量和速度矢量为

(27)

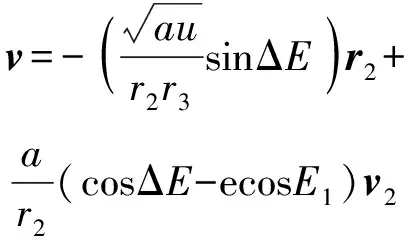
(28)

即拦截弹的飞行状态信息。

2.3 相关约束条件

时间约束，由椭圆方程可知对于给定的、两点，通过、两点的椭圆弹道有无穷多条。对于反导拦截，需要考虑的是飞行时间的约束，主要是指目标和拦截弹在同一时刻同时运动到预测遭遇点位置。因此给定了拦截弹的飞行时间之后，则可唯一地确定出通过拦截点和遭遇点的弹道。

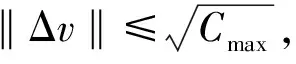
初始段飞行程序约束，由于拦截弹在大气层内飞行过程受力非常复杂，而且初始段拦截弹的飞行弹道一般是按预先设定的控制程序飞行，初始段的弹道难以按照理论规划弹道飞行，实际的飞行弹道与拦截弹初始段的飞行程序有关。

3 仿真计算

3.1 模型验证

在大地惯性坐标系下，假设时刻获取弹道导弹发动机关机后点的状态位置矢量为(2.945 36×10m，5.998 132×10m，2.967 413×10m)，速度矢量为(-2.659 2×10m/s，2.172 93×10m/s，3.326 04×10m/s)。假设拦截弹的发射点坐标为(-2.882 326×10m，4.541 819×10m，3.416 752×10m)。以时刻为起始时间，则目标落地时刻为1 011 s，下面对拦截弹道规划模型进行仿真验证。其中图2所示为飞行时间分别为500 s、600 s、700 s，不同遭遇点位置下拦截弹道的规划结果。图3所示为飞行时间分别为500 s、600 s、700 s，相同遭遇点位置下拦截弹道的规划结果。图4为飞行时间为500 s，不同遭遇点位置下拦截弹道的规划结果。

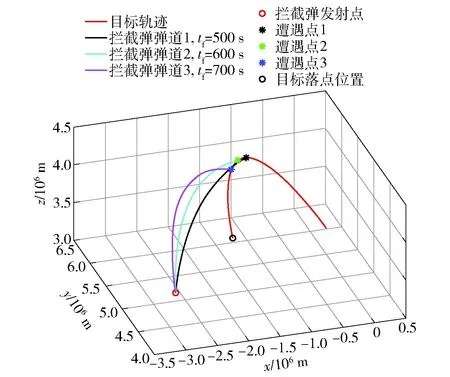
图2 不同拦截点不同飞行时间仿真结果Fig.2 Simulation results of different interception points and different flight durations

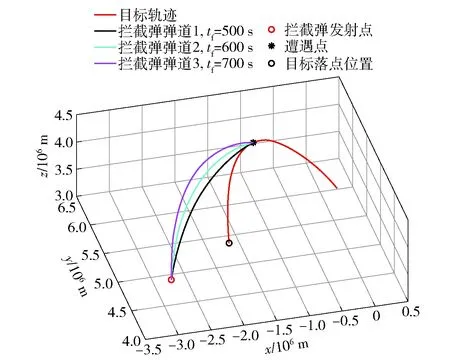
图3 相同拦截点不同飞行时间仿真结果Fig.3 Simulation results of different flight durations at the same interception point

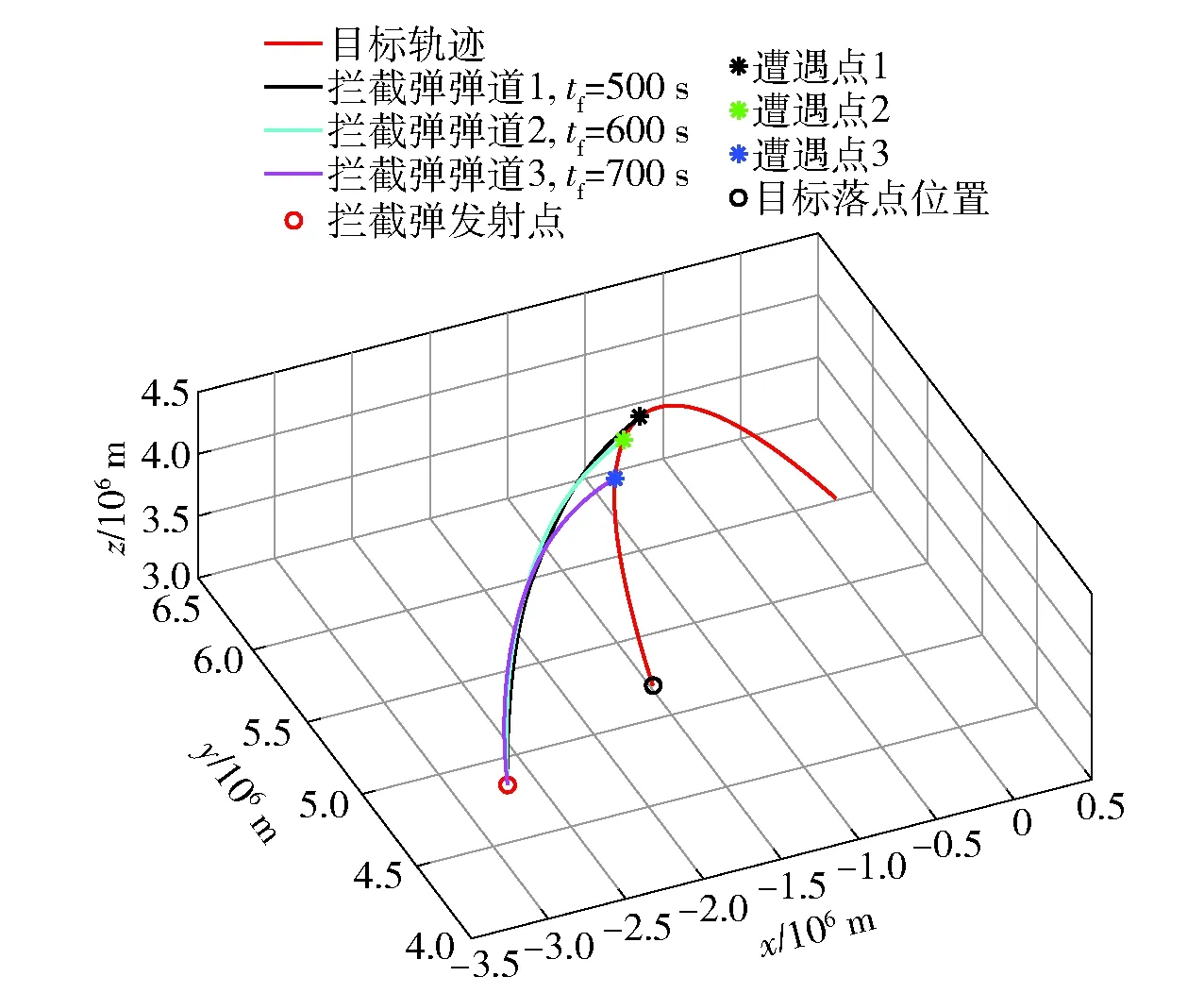
图4 不同拦截点相同飞行时间仿真结果Fig.4 Simulation results of the same flight duration at different intercept points

假设拦截弹主动段结束时刻即发动机关机点距离地面高度为100 km，遭遇点为目标从起始时刻飞行700 s的位置(-1 487 113 m，5 535 938 m，4 280 217 m)，设拦截弹飞行时间为300～700 s，仿真计算拦截弹主动段发动机关机点以及与目标遭遇点的速度随飞行时间的变化曲线如图5所示。由图5可知，在同一遭遇点，拦截弹发射时间越早，所需的关机点速度越小。假设拦截弹的速度受到最大发射能量约束，可进一步约束飞行时间的取值范围。

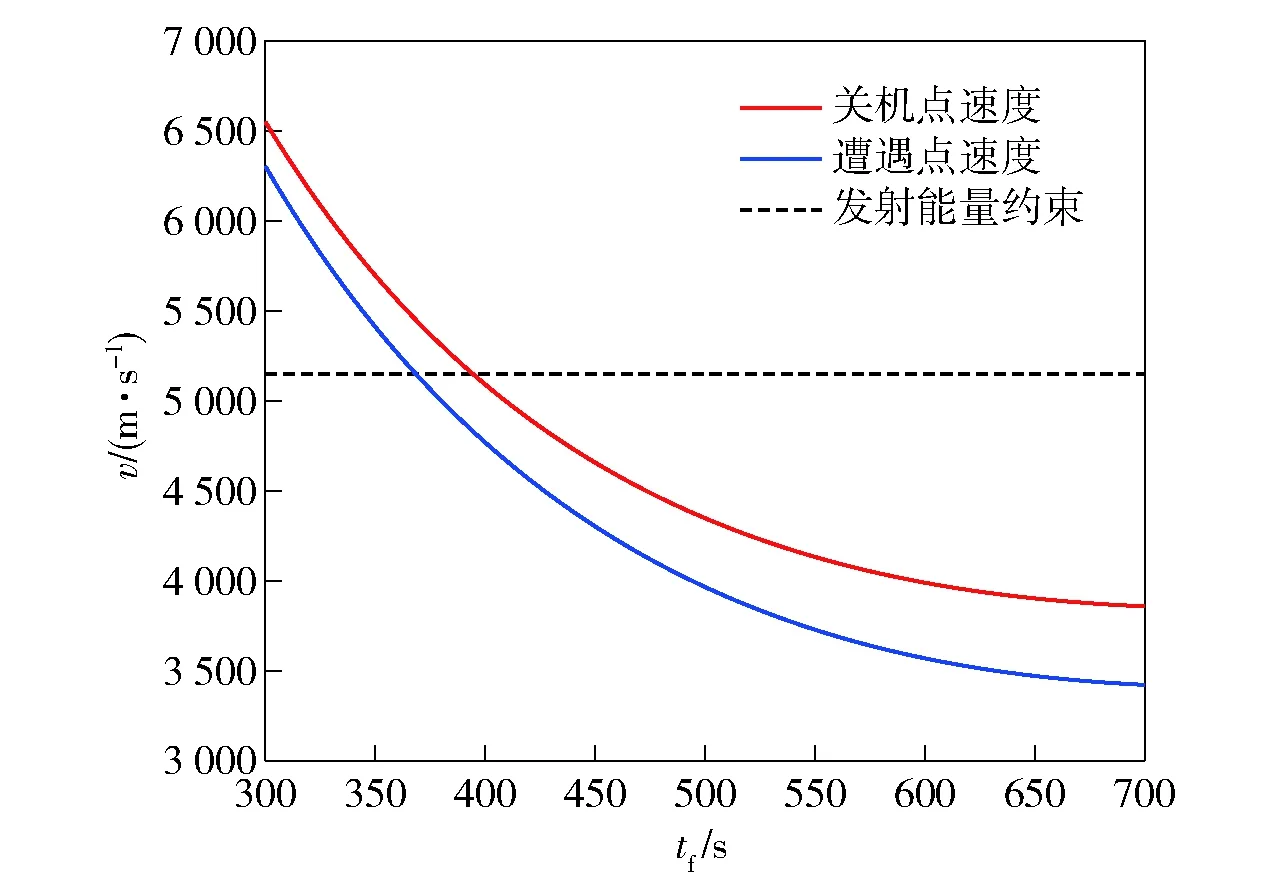
图5 拦截弹发动机关机点、遭遇点速度随tf的变化曲线Fig.5 Curves of variation of velocity at the interceptor’s shutdown point and impact point with tf

利用图2中的仿真参数，根据模型可计算出关机点处的位置矢量和速度矢量，具体参数如表1所示，以表1中拦截弹关机点的参数可作为主动段飞行程序的设计指标。同样也可解得遭遇点处目标与拦截弹的运动参数，具体的参数如表2所示。对比分析表2中的遭遇点参数可知，在遭遇点1、遭遇点2、遭遇点3处拦截弹与目标的距离偏差分别为|Δ|=925 m，|Δ|=956 m，|Δ|=1 092 m。一般情况拦截弹的末制导机动范围可达几千米，在拦截弹末制导控制下拦截弹有能力修正飞行弹道的偏差，实现拦截弹与目标的遭遇，所以规划的拦截弹道在理论上能够满足中段反导拦截作战要求。

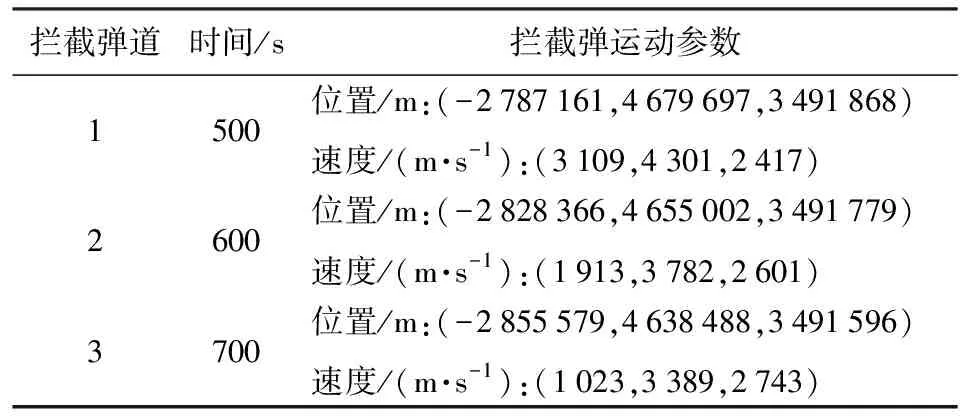
表1 拦截弹关机点位置和速度

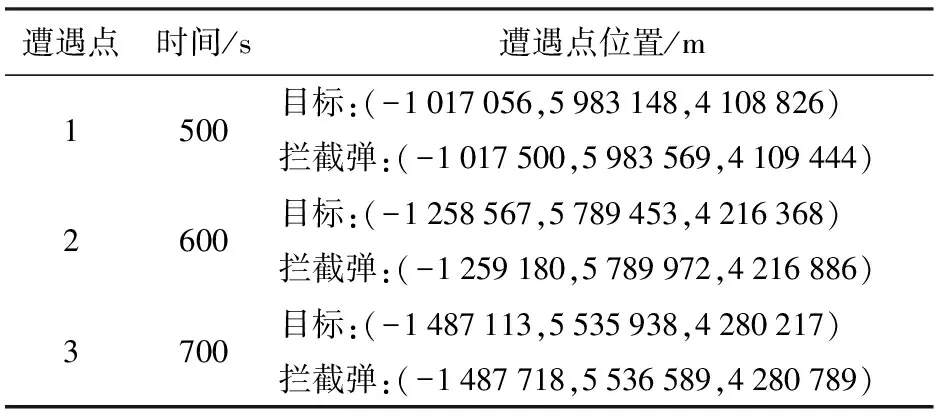
表2 遭遇点参数

3.2 拦截解算

依据本文构建的拦截弹道模型，在相关约束条件下对反导拦截作战的整个作战过程进行仿真分析。拦截弹的发射点位置为(-2.882 326×10m，4.541 819×10m，3.416 752×10m)，以美军地基中段防御系统的相关拦截能力为参照，假设拦截弹的拦截低界为200 km、拦截高界为2 000 km、拦截斜距为4 000 km，最大速度增量为5 200 m/s，下面对拦截弹的发射窗口、可拦截弧段进行仿真计算。仿真结果如图6、图7所示。其中，图6为拦截弹在发射时间和飞行时间两个维度上的发射窗口，蓝色区域为拦截窗口，表示拦截弹在相应的飞行时间和发射时间约束下发射可实现对目标的拦截；图7为在拦截弹在拦截能力约束下对弹道导弹目标的可拦截弧段解算结果。根据拦截弹拦截能力约束下的发射窗口和可拦截弧段参数，可进一步指导修正拦截弹的设计。

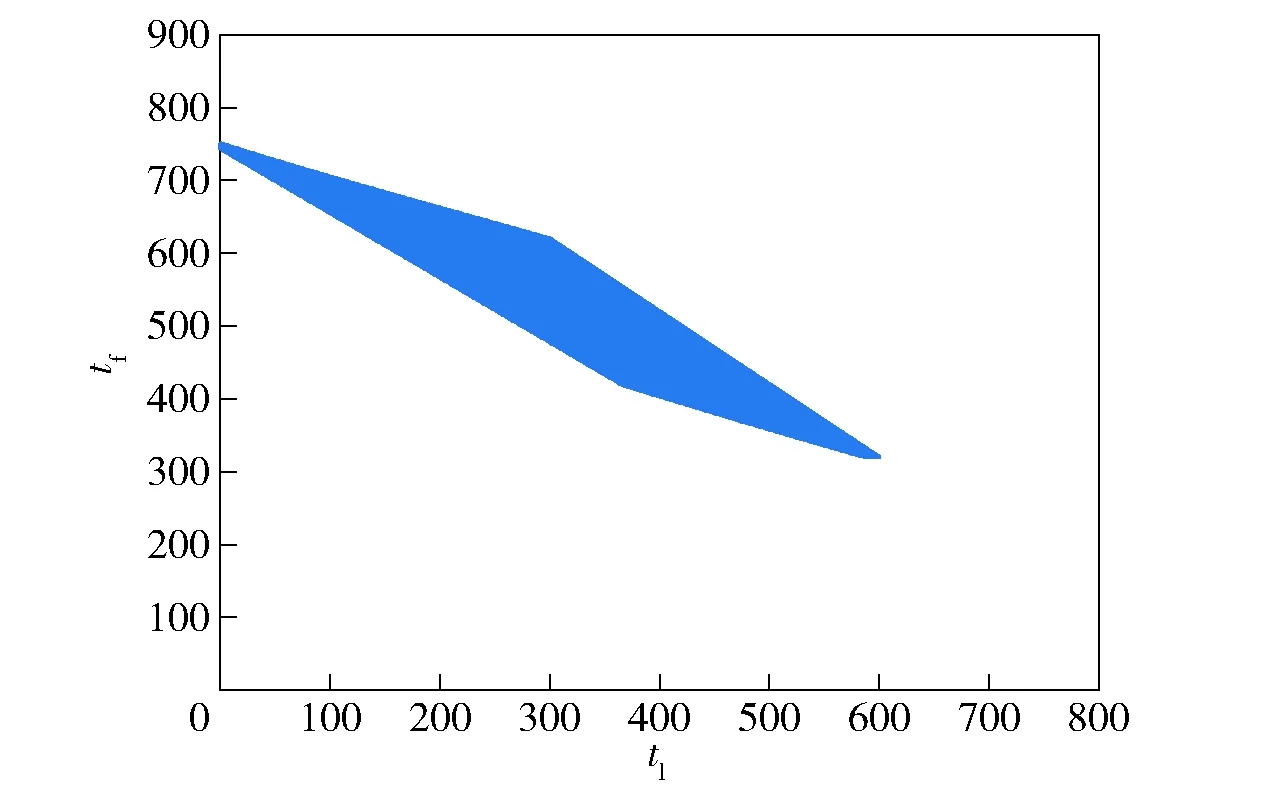
图6 拦截弹二维发射窗口Fig.6 Two-dimensional launch window of the interceptor

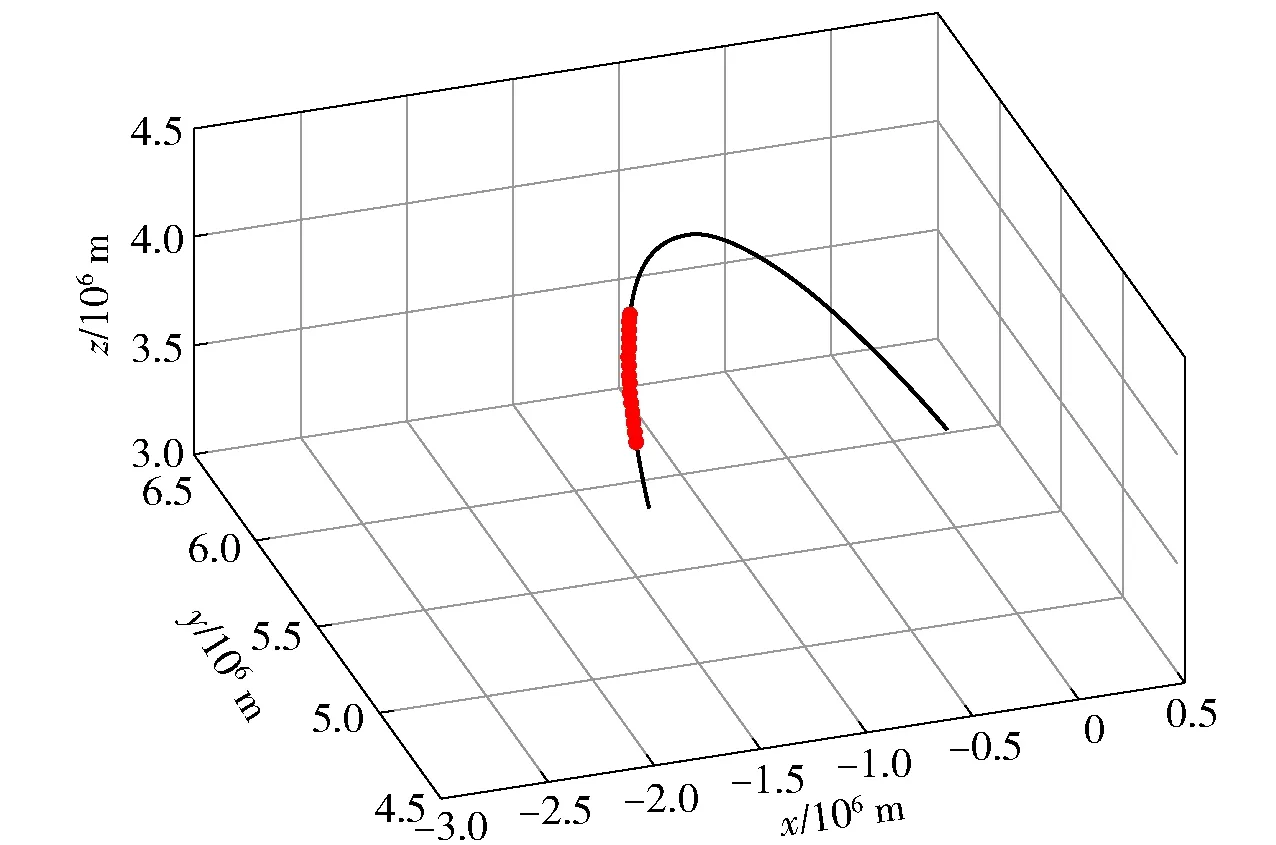
图7 可拦截弧段解算结果Fig.7 Interceptable arc calculation results

4 结论

1)建立了反弹道导弹中段拦截弹道规划模型，并通过仿真计算验证了弹道规划模型的有效性。

2)所建立的拦截弹弹道模型能够在发射时间和飞行转移时间维度上对弹道导弹拦截窗口进行解算，并且可以依据拦截弹的拦截能力对弹道导弹的可拦截弧段进行计算。

3)该模型为拦截弹道规划设计提供了一种思路和方法，对中段拦截弹道规划设计具有一定的参考和借鉴意义。

[1] 高昂，胡延苏. 基于概率模型的弹道导弹防御系统拦截方案优化与评估[J].兵工学报，2016，37(2): 379-384.

GAO A，HU Y S. The optimization and evaluation of ballistic missile defense system interception scheme based on probability model[J]. Acta Armamentarii, 2016, 37(2): 379-384. (in Chinese)

[2] 张毅，杨辉耀，李俊莉.弹道导弹弹道学[M].长沙:国防科技大学出版社，1999.

ZHANG Y，YANG H Y，LI J L. Ballistic missile ballistics[M].Changsha: National University of Defense Technology Press，1999. (in Chinese)

[3] 刘瑶，张占月，王磊. 中段反导火力单元优化部署研究[J].火力与指挥控制，2018，43(5):157-161.

LIU Y，ZHANG Z Y，WANG L. Research on the optimal deployment of the mid-section antimissile firepower unit[J]. Firepower and Command Control，2018，43(5): 157-161. (in Chinese)

[4] 杨光宇，陈国光，王捷，等. 基于PSO-SQP算法的空地导弹弹道优化[J].兵器装备工程学报, 2021, 42(5): 153-157.

YANG G Y, CHEN G G, WANG J, et al. Trajectory optimization of air to ground missile based on PSO-SQP algorithm[J]. Journal of Ordnance Equipment Engineering, 2021, 42(5): 153-157. (in Chinese)

[5] 张浩，张奕群，张鹏飞. 拦截主动防御目标的微分对策制导律[J].系统工程与电子技术, 2021, 43(5): 1335-1345.

ZHANG H, ZHANG Y Q, ZHANG P F. Differential game guidance law for intercepting the active defense target[J].Systems Engineering and Electronic Technology, 2021, 43(5): 1335-1345. (in Chinese)

[6] 柴华.基于可达集的大气层外导弹防御系统不确定性交战分析[D].长沙: 国防科技大学，2015.

CHAI H. Analysis on uncertain combat of exoatmospheric missile defense system based on reachable set[D]. Changsha: University of Defense Science and Technology，2015. (in Chinese)

[7] 王莎，刘进忙，李超，等.中段高精度弹道预测方法研究[J].科学技术与工程，2013，13(23):6683-6687.

WANG S，LIU J M，LI C，et al. Research on high precision trajectory prediction method in midcourse[J].Science，Technology and Engineering，2013，13(23):6683-6687.(in Chinese)

[8] 杨少春，刘永兰，刘进忙.采用分段思想的中段弹道预测算法[J].空军工程大学学报(自然科学版)，2014，15(3):33-36.

YANG S H，LIU Y L，LIU J M. The middle trajectory prediction algorithm using segmented thinking[J]. Journal of Air Force Engineering University (Natural Science Edition), 2014, 15(3): 33-36. (in Chinese)

[9] 周啟航，张刘，霍明英.弹道导弹中段突防弹道设计与验证[J].光学精密工程，2015，23(9): 2645-2655.

ZHOU Q H，ZHANG L，HUO M Y. Design and verification of ballistic missile midcourse penetration trajectory[J]. Optical Precision Engineering, 2015, 23(9): 2645-2655. (in Chinese)

[10] 方群，李新国，朱战霞，等.航天飞行动力学[M].西安:西北工业大学出版社，2015.

FANG Q, LI X G, ZHU Z X, et al. Space flight dynamics [M]. Xi’an: Northwestern Polytechnic University Press, 2015. (in Chinese)

[11] BATTIN R H. Lambert’s problem revisited[J]. AIAA Journal，1977，15(5):705-713．

[12] 柴华，仲明，梁彦刚.采用状态转移矩阵的拦截中段制导方法[J].国防科技大学学报，2015，37(4):137-142.

CHAI H，ZHONG M，LIANG Y G. Intercepting midcourse guidance method using state transition matrix[J].Journal of National University of Defense Science and Technology，2015，37(4): 137-142. (in Chinese)

[13] 吴启星，张为华.弹道导弹中段防御的拦截窗口分析[J].飞行力学，2005，23(2):56-58.

WU Q X，ZHANG W H. Analysis of intercepting window of ballistic missile midcourse defense [J]. Flight Mechanics，2005，23(2):56-58. (in Chinese)

[14] AVANZINI G，PALMAS A，VELLUTINI E．Solution of low-thrust Lambert problem with perturbative expansions of equinoctial elements[J]. Journal of Guidance, Control, and Dynamics, 2015, 38(8): 1585-1601.

[15] SCHUMACHERJR P W, SABOL C, HIGGINSON C, et al. Uncertain Lambert problem[J]. Journal of Guidance，Control, and Dynamics, 2015, 38(7): 1573-1584．

[16] 徐利民，张涛，陶佳伟. 能量最优与燃料最优Lambert交会问题[J].北京航空航天大学学报，2018，44(9):1888-1893．

XU L M，ZHANG T，TAO J W. Energy optimal and fuel optimal Lambert rendezvous problem[J]. Journal of Beijing University of Aeronautics and Astronautics，2018，44(9):1888-1893. (in Chinese)

[17] WEN C，ZHAO Y，SHI P．Derivative analysis and algorithm modification of transverse-eccentricity-based Lambert problem[J].Journal of Guidance, Control, and Dynamics, 2014, 37(4): 1195-1201.

[18] 茅永兴，何晶.航天器轨道确定的单位矢量法[M].北京:国防工业出版社，2009.

MAO Y X, HE J. Unit vector method for spacecraft orbit determination[M]. Beijing: National Defense Industry Press，2009.(in Chinese)