湍流大气中随机粗糙表面激光回波空间相干性仿真*
2022-07-28李艳玲梅海平任益充张骏昕陶志炜艾则孜姑丽阿不都克热木刘世韦
李艳玲 梅海平 任益充 张骏昕 陶志炜 艾则孜姑丽·阿不都克热木 刘世韦
1) (中国科学院合肥物质科学研究院,安徽光学精密机械研究所,中国科学院大气光学重点实验室,合肥 230031)
2) (中国科学技术大学研究生院科学岛分院,合肥 230026)
3) (中国科学技术大学环境科学与光电技术学院,合肥 230026)
4) (先进激光技术安徽省实验室,合肥 230037)
根据广义Huygens-Fresnel 原理,推导了von Karman 湍流谱条件下激光回波复相干度的理论解析式;基于湍流相位屏分步传输算法和随机粗糙目标表面模型,实现了激光回波光场的仿真计算.首先通过镜面反射回波光场的仿真分析,验证了算法的正确性;然后基于1.1 km 的均匀传输路径,综合分析了随机粗糙目标表面特性和路径湍流强度对回波光场复相干度的影响.结果表明:回波光场的空间相干性随目标表面高度均方根的增大而降低,随目标表面相关长度的减小而降低;当表面相关长度远小于大气相干长度时,回波相干性会被严重破坏.该研究可为目标表面特性或利用已知表面获取路径湍流状态的相干探测提供有益的参考.
1 引言
受湍流大气的影响,激光遇到目标反射面后,其回波的振幅和相位会发生随机涨落[1,2].一方面,利用该现象可以获取激光传输路径上的大气湍流参数,如湍流强度、特征尺度、矢量风速等[3−10];另一方面,由此引起的退相干效应严重制约了激光外差、合成孔径成像雷达等相干探测技术在大气中的应用[11−14],因为激光回波信号的复相干度(complex degree of coherence,DOC)直接反映了其与本征光的相干效率,从而影响相干探测的信噪比和可行性[15].Andrews 等[15−17]基于Kolmogorov 湍流统计理论,推导了湍流大气中激光单程传输光场的DOC 解析表达式.针对有限漫反射目标的简化模型,Korotkova 和Andrews 等[18,19]利用ABCD矩阵理论推导了回波光场的DOC 解析表达式.这些研究给出了激光光场DOC 的基本概念,同时建立了大气湍流影响激光回波光场相干特性的理论基础.
受大气湍流和目标表面反射特性的共同作用,利用解析理论难以计算激光回波振幅和相位的时空分布.因此,常采取数值模拟的方法来仿真计算.早期的仿真侧重激光在随机介质中单程传输,包括其特性研究和算法改进,如点光源的闪烁[20,21]、球面波的长距离单程传输导致网格分辨率降低的问题[22]、分步光传输算法改进[23]等.受激光雷达研究需求的驱动,针对激光往返传输的仿真研究得到重视[24−28].其中Li 等[28]考虑以平面镜、角反射镜为反射目标,对激光回波的相干长度、闪烁指数等进行了数值分析.但上述仿真研究仅限于回波光强,未涉及相位及空间相干特性,也未考虑粗糙目标表面特性对激光回波的影响,尚不能满足激光相干探测的计算需求.
基于此,本文拟通过建立可靠的数值仿真算法,综合分析目标反射特性和大气湍流对回波光场空间相干性的影响.首先,根据激光往返传输几何模型,简要梳理DOC 和相位结构函数(phase structure function,PSF)的基本概念,并且基于von Karman 湍流谱模型,在水平均匀路径上推导出含特征尺度的DOC 和PSF 解析式;进一步在理想镜面反射条件下,将DOC 和PSF 的解析解与数值仿真结果进行对比,验证算法的合理性;最后,通过改变目标表面粗糙度和激光传输路径上的光学湍流特征参数,获得对激光回波空间相干性的规律性认识.
2 回波光场的DOC 和PSF
激光从发射端出发,经过湍流路径到达距离为L处的目标反射面后,再经过同一路径返回到接收端,最后进行二维成像探测.将该过程在空间上展开后,其传输模型如图1 所示[18].图1 中令发射端的初始光场为u0(x0,y0,0),到达目标靶面处的光场为ut(xt,yt,zt=L),回到接收平面处的光场为ur(xr,yr,zr=2L),则经过成像系统后在焦平面处的光场为uf(xf,yf,zf).
2.1 回波光场表达式
根据广义Huygens-Fresnel 原理,在旁轴近似条件下,光场u0通过大气湍流传输到成像系统入瞳处的频谱为[29]
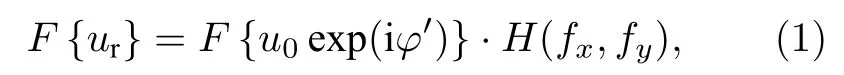
其中F表示Fourier 变换,表示大气湍流引起的随机相位起伏.

为Fresnel 衍射在频域的传递函数[29],其中λ表示波长,波数k=2π/λ;zr=2L表示光在大气中的往返传输距离;表示空间频率.
考虑如图1 所示的传输模型,结合文献[8]中的反射项T,令T=RWexp(i2kfscrn),其中目标反射面的反射率为R,孔径函数为W,高度分布为fscrn,2kfscrn为反射面引起的相位起伏,则成像系统入瞳处的频谱为
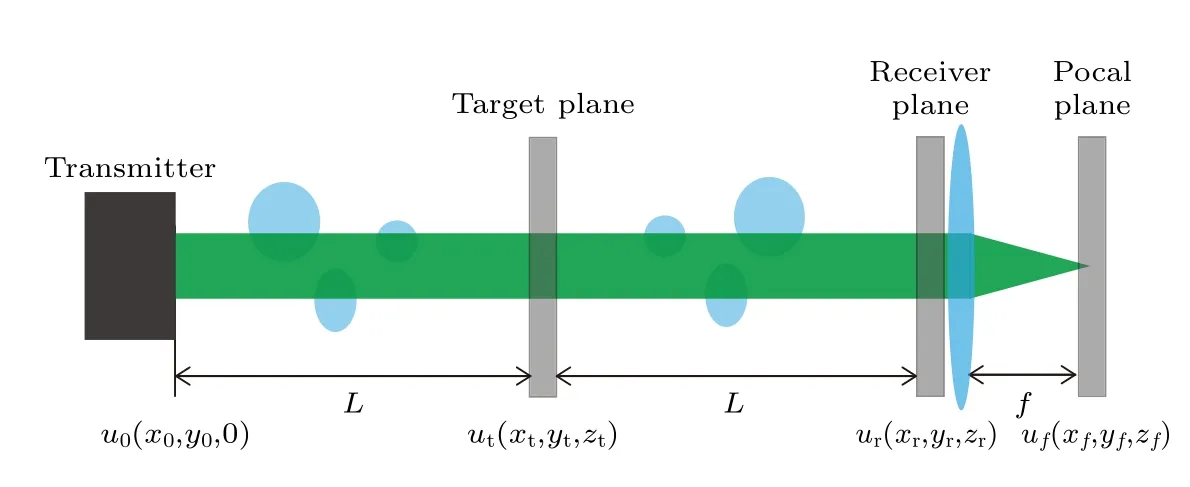
图1 激光经过湍流大气双程传输示意图(展开模式)Fig.1.Schematic of double-passage retroreflected laser propagation through atmospheric turbulence (unfolded).
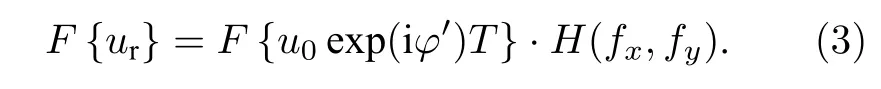
对(3)式进行Fourier 反变换得到接收平面处的场分布为
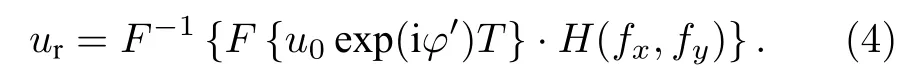
根据透镜的Fourier 变换性质,得到成像系统后焦面上的场分布为[29]

其中,f表示成像系统的焦距.
2.2 回波光场的空间相干性
2.2.1 回波光场的DOC
DOC 反映了回波光场在空间两点间相干性的强弱,根据光场的二阶统计理论,DOC 定义为光场的归一化互相关函数[19]:
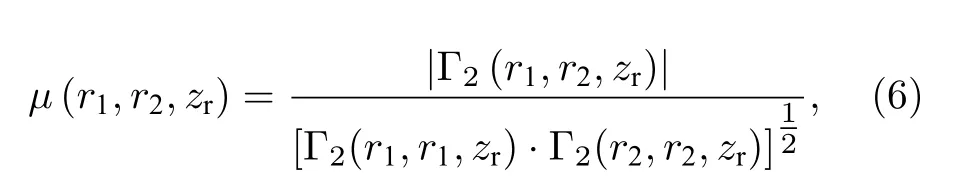
其中r1,r2是接收平面上的两点.互相关函数定义为[16]
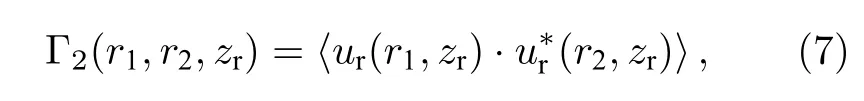

其中Δr=|r2-r1|表示空间距离,µscrn(Δr,zr)为真空中目标反射面对DOC 的影响,µatm(Δr,zr)为大气湍流对DOC 的影响.µscrn(Δr,zr)可表示为[18]
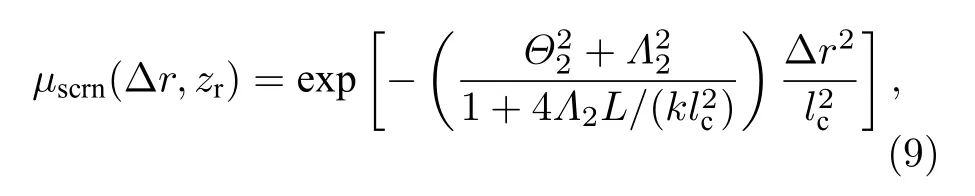
式中,L为光束到目标反射面之间的距离;Θ2=1+L/F2,F2表示回波波前曲率半径;W2为回波光束半径;lc为粗糙目标反射面的横向相关长度,lc→∞表示理想镜面,lc→0表示漫反射表面.
大气湍流对DOC 的影响可表示为[30]
其中κ(rad/m)表示空间角频率,Φn(κ,z)表示大气折射率功率谱,J0表示一阶贝塞尔函数.Schmidt[30]根据(10)式推导了Kolmogorov 谱条件下传输光场的DOC,但是Kolmogorov 谱假定湍流内尺度等于零、外尺度趋于无穷大.为了兼顾有限的外尺度条件,本文选用von Karman 谱模型来推导更为精确的DOC 表达式.
假定激光传输路径水平均匀,根据简化的von Karman 谱模型[30]:
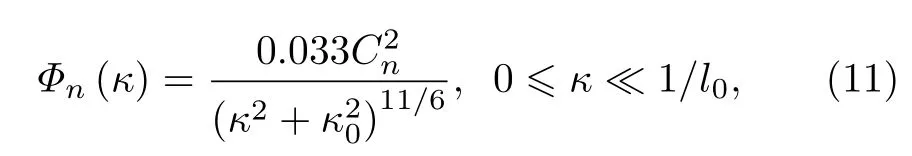
式中κ0=2π/L0,L0为湍流外尺度,为折射率结构函数.结合贝塞尔函数的积分公式

通过变量替换,可得接收平面处的DOC 为

受大气湍流和粗糙反射面的共同作用,通过解析理论难以确定回波的曲率半径和光束半径,所以无法通过(9)式计算复相干度µscrn(Δr,zr);为解决这一问题,可利用粗糙反射面回波光场的仿真结果,定量计算其DOC.而在理想镜面反射条件下,目标反射面不引起相位起伏,即µscrn(Δr,zr)≈1,所以µ(Δr,zr)≈µatm(Δr,zr),则可根据(13)式计算双程传输后的µatm(Δr,zr),以获得激光回波的复相干度µ(Δr,zr).
2.2.2 回波光场的PSF
DOC 与波前结构函数D(Δr,zr)的关系为[19]
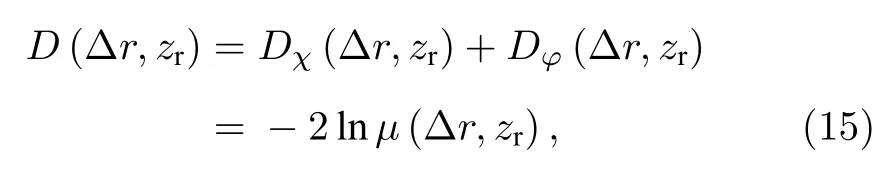
式中Dχ(Δr,zr)表示对数振幅结构函数,Dφ(Δr,zr)表示PSF.考虑几何光学近似条件2Lκ2/k≪1,Dχ(Δr,zr)≈0,Dφ(Δr,zr)≈D(Δr,zr).
根据目标反射面和大气湍流共同作用下的结构函数与DOC 之间的关系[18]:
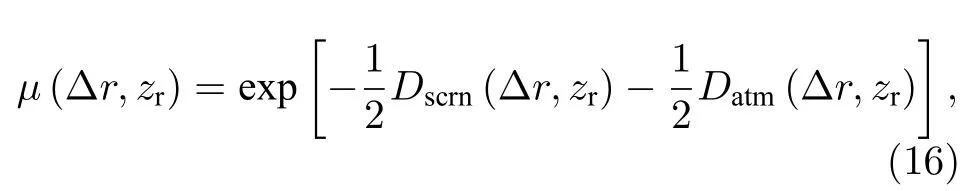
其中,Dscrn(Δr,zr)表示目标反射表面对结构函数的影响,Datm(Δr,zr)表示大气湍流对于结构函数的影响.Dscrn(Δr,zr)的表达式为[18]

考虑理想镜面反射时,Dscrn(Δr,zr)≈0,Dφ(Δr,zr)≈Datm(Δr,zr).综上所述,通过理论推导给出了von Karman 湍流谱模型下回波光场的DOC 表达式与PSF 表达式.后续计算镜面反射条件下的解析解,可用来检验激光传输仿真程序的可靠性.
3 目标表面反射回波数值仿真算法
3.1 无限长相位屏生成原理
基于随机相位屏的光传输数值模拟算法原理是将长度为zr的连续随机介质分割为距离为Δz的等间隔区域,光束依次在每个区域经历真空衍射和相位屏调制,直至接收表面.上述过程的核心是相位屏的生成,目前有两种生成相位屏的方法,一是基于快速傅里叶变换[31,32],二是基于协方差[33].Assemat 等[34]提出基于协方差的无限长相位屏仿真算法具有高精度、长曝光、可计算非稳态湍流的特点,本文选择该方法生成相位屏.
首先利用功率谱反演法生成初始的二维随机相位屏φ,根据风速、风向、迭代时间计算每次迭代需要移动的像素数Nmove(行或列),然后在φ中选择靠边缘的若干行或列构建矩阵Z,再由矩阵Z 按照(20)式生成需要增加的行或列X[34]:

最后将X 添加到φ中紧邻矩阵Z 的一侧,同时切除另一侧多出来的数据.(20)式中β 表示均值为0、协方差为1的高斯随机向量,矩阵A 和B 通过文献[34]X和Z的协方差包括计算得到,这些协方差矩阵都是通过构造距离矩阵ri,j,并将其作用于相位协方差函数Cφ(ri,j)上来获得.在von Karman 湍流谱条件下,相位协方差计算表达式为[19]
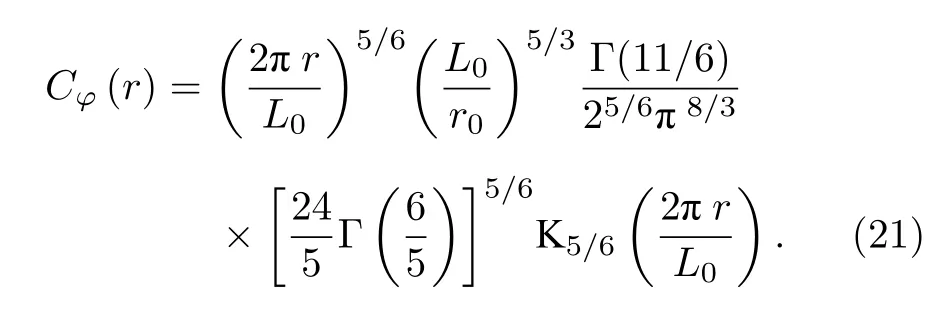
3.2 基于蒙特卡罗法的随机粗糙面仿真模型
为了与解析理论对比,将目标反射面考虑为平面镜来分析激光回波的DOC 和PSF.但相对光波而言,实际的目标反射面是二维随机粗糙面,通常采用蒙特卡罗法将粗糙面上某点的高度表示为[35]

δh表示二维粗糙面的高度均方根.将(23) 式和(24)式代入(22)式,可获得指定几何面型的二维随机粗糙面,图2 为选取不同参数的粗糙面.
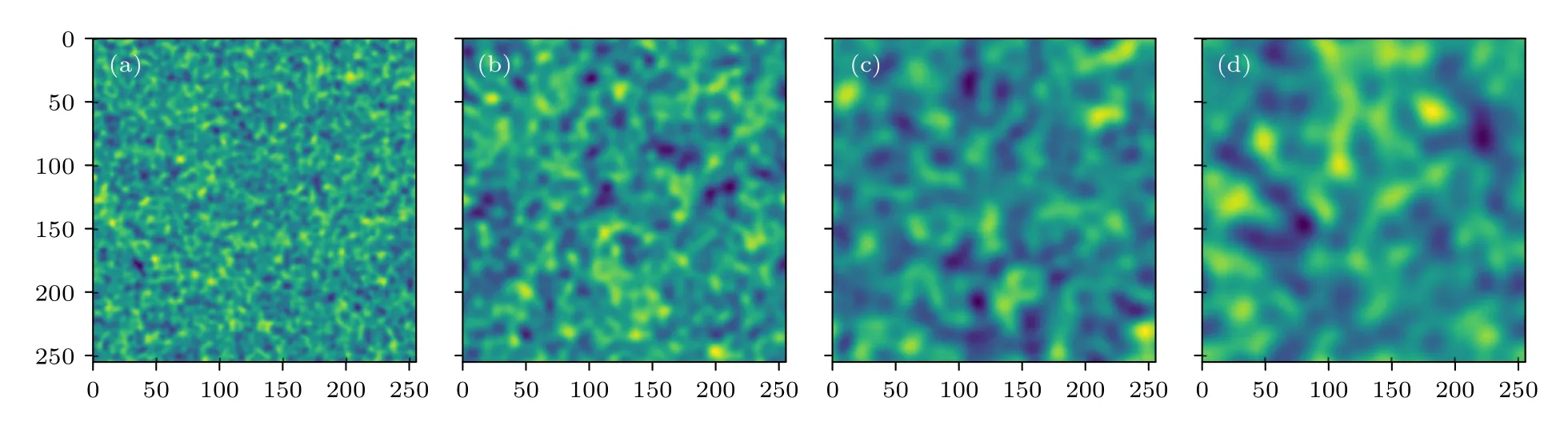
图2 δh=10-2λ时,不同表面相关长度的粗糙面 (a) Lx=0.1 m;(b) Lx=0.2 m;(c) Lx=0.3 m;(d) Lx=0.4 mFig.2.Gaussian rough surface with different characteristic parameters for δh=10-2λ:(a) Lx=0.1 m;(b) Lx=0.2 m;(c) Lx=0.3 m;(d) Lx=0.4 m.
3.3 湍流大气中往返传输的光束仿真
基于无限长相位屏和随机粗糙面生成原理,采用图3 所示的分步光传输模型来仿真激光的往返传输.在前向传输路径上等间隔地设置N个湍流无限长随机相位屏,然后加载目标靶面相位屏,最后以目标靶面为镜像面,通过设置空间对称分布的湍流相位屏计算返程传输过程.通过调节反射面的粗糙度特征参数,即可获得目标表面特征对激光往返传输特性的影响情况.考虑1100 m 的往返传输路径,即展开模式下传输2200 m,根据离散相位屏代替连续介质对间距的要求[20,25]:同时相邻相位屏应满足统计独立,即相位屏的间距应大于湍流介质的外尺度,即Δz >L0.结合上述条件,每间隔100 m 设置1 张相位屏,仿真的参数设置如表1.
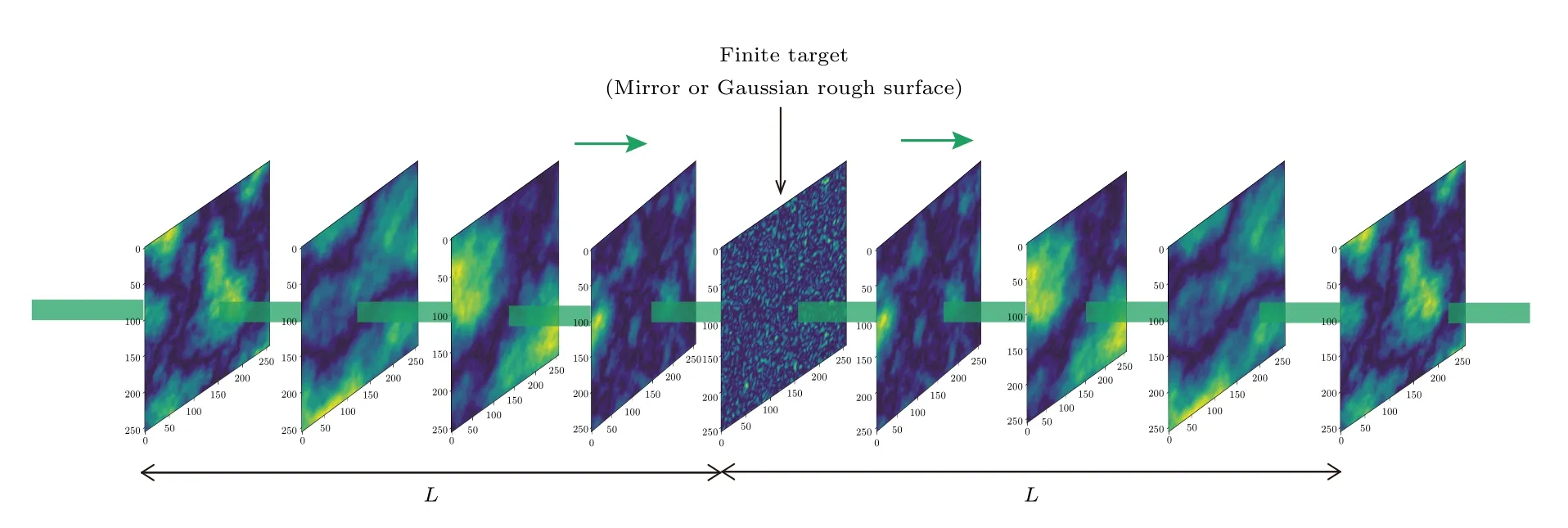
图3 基于无限长相位屏和随机粗糙面的回波光场仿真模型(展开模型)Fig.3.Simulation model of echo light field based on infinitely long phase screen and random rough surface (unfolded).

表1 回波光场仿真参数选取Table 1.Echo wave light field simulation parameter selection.
4 仿真结果与讨论
首先,通过仿真获得回波接收光场与成像系统焦平面的光场,并展示其光斑分布特征;然后,在理想的镜面反射条件下,利用仿真结果统计回波光场的DOC 和PSF,将该结果与相同湍流条件下的理论值进行对比,以检验激光大气传输过程仿真的可靠性;最后分析DOC 随粗糙面特征参数和湍流强度的变化.
4.1 回波光场的强度分布
通过仿真水平传输路径的回波接收光场,并计算像平面的散斑场,结果如图4 所示,横纵坐标单位是像素.图4(a)为镜面反射条件下、大气相干长度r0=0.1 m 时的回波光强分布;图4(b)为图4(a)在成像系统像平面的光斑;图4(c)为相同的镜面反射条件,r0=0.04 m 时的回波接收光斑;图4(d)为图4(c)在成像系统像平面的光斑.图4(e)为随机二维粗糙面(Lx=0.1 m、δh=10-2λ)反射条件下、r0=0.1 m 时的回波接收光斑;图4(f)为图4(e)在成像系统像平面的光斑;图4(g)为与图4(d)相同反射条件下、r0=0.04 m 时的回波接收光斑;图4(h)为图4(g)在成像系统像平面的光斑.在湍流较强时,接收平面形成纹理清晰的渔网状结构,并存在零散分布的锐利亮点的光斑,如图4(c),(g)所示,由于风速影响,可观察到光斑的破碎和漂移;在像平面处形成的动态散斑场形态如图4(d),(h)所示,在仿真获得的回波光场的基础上,下文继续开展回波光场空间相干性的仿真研究.
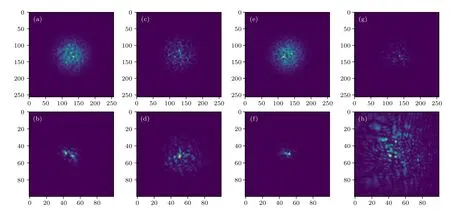
图4 接收平面光斑及像焦平面上的散斑分布,前两列目标反射面为平面镜 r0=0.1 m,接收平面光斑 (a)和焦平面光斑 (b);r0=0.04 m,接收平面光斑(c)和焦平面光斑(d);后两列目标反射面为高斯粗糙面 r0=0.1 m,接收平面光斑(e)和焦平面光斑(f);r0=0.04 m,接收平面光斑(g)和像平面光斑(h)Fig.4.Light intensity at the receiver plane and the speckle intensity on the image plane,the first two columns of target reflecting surface are plane mirrors:r0=0.1 m,the light intensity at the receiver plane (a) and the light intensity at focal plane (b);r0=0.04 m,the light intensity at the receiver plane (c) and the light intensity at focal plane (d);the second two columns of target reflection surfaces are Gaussian rough surfaces:r0=0.1 m,the light intensity at the receiver plane (e) and the light intensity at focal plane (f);r0=0.04 m,the light intensity at the receiver plane (g) and the light intensity at focal plane (h).
4.2 回波光场相位解包裹原理
为了分析回波接收光场的相位特性,需要从仿真得出的光场复振幅中提取对应的相位值,但直接通过幅角提取的相位值被包裹在-π—π之间,因此需要对其进行解包裹处理.鉴于质量导引路径法在解包裹时具有稳定性以及高效性,本文对接收光场的相位采用文献[36]提出的算法进行二维快速解包裹.
1)选择可靠性函数:图像像素的二阶差分反映相位的高低起伏程度,定义二阶差分值的倒数为可靠性函数.将图像边界的二阶差分设为无穷,除边界以外其他像素点的二阶差分可通过相邻像素计算得到.
2)设计展开路径:将可靠性函数作为选择相位解包裹路径的依据,对边界的可靠性进行排序,随后从可靠性的最大值开始依次进行解包裹.
对图像边界所有元素进行解包裹处理后,选择紧邻边界的部分继续展开边界重复上述步骤,直至完成整幅图像的相位解包裹.
4.3 湍流大气中镜面反射的回波DOC 及PSF
在镜面反射条件下,令初始光束半径为0.2 m,往返传输距离2L=2200 m,接收平面尺寸为1 m,对应的网格数为256×256,选取r0=0.10,0.04 m,并在传输路径上对称地设置20 张无限长相位屏.仿真结果如图5 和图6 所示,其中图5(a)和图6(a)为真空传输时接收平面处的光斑,即光强空间分布;图5(b)和图6(b)为湍流大气中接收平面处的光斑,可见湍流越强,回波光斑中的网纹状结构越明显;图5(c)和图6(c)为在接收平面中心处选取100×100个网格点的正方形区域的包裹相位,结果表明湍流越强,相位的波动越剧烈、相位变化程度越大,出现的包裹削线越多[37,38];图5(d)和图6(d)分别为对图5(c)和图6(c)进行解包裹后的相位.

图5 不同大气条件下,接收平面处的回波光强和相位(目标反射面为理想平面镜) (a) 自由空间的接收光斑;(b) r0=0.1 m,经过湍流的回波光斑;r0=0.1 m,回波光场的(c)包裹相位和(d)解包裹相位Fig.5.The echo light intensity and phase at the pupil plane under different atmospheric conditions (the target reflecting surface are plane mirrors):(a) Receiving light intensity in free space;(b) receiving light intensity in turbulence atmosphere at r0=0.1 m;wrapped phase (c) and unwrapped phase (d) of the echo light intensity at r0=0.1 m.

图6 不同大气条件下,入瞳处的回波光强和相位分布(目标反射面为理想平面镜) (a) 自由空间接收光斑;(b) r0=0.04 m,经湍流的回波光斑;r0=0.04 m,回波光场的(c) 包裹相位和(d) 解包裹相位Fig.6.The echo light intensity and phase at the pupil plane under different atmospheric conditions (the target reflecting surface are plane mirrors):(a) Receiving light intensity in free space;(b) receiving light intensity in turbulence atmosphere at r0=0.04 m;wrapped phase (c) and unwrapped phase (d) of the echo light field at r0=0.04 m.
在每一帧解包裹后的回波相位面上,从中心点开始选取间距为Δr的两点,并将Δr从0 逐渐增加0.4 m,得到不同间距上的PSF.由于单帧图像的随机性较大,取600 个样本的统计平均值,得到图7 中较为平滑的PSF 变化曲线.同时与(18)式计算得到PSF 理论值进行比较.结果表明,在两种湍流状态下,仿真实现的PSF 与理论预期基本一致.进一步,利用相同大小的样本,通过计算回波光场复振幅的归一化互相关函数得到DOC,然后统计平均得到如图8 所示的DOC 变化曲线.将其与(13)式计算得到的DOC 理论值进行比较,发现DOC 的仿真结果与理论值在Δr较小时基本一致,在Δr较大时出现一定的偏差.分析产生该偏差的主要原因是:利用快速傅里叶变换计算两点间的相关性会造成Δr较大时出现旁瓣现象,导致DOC升高,该结果与文献[30]中的情况相同,但是这种偏移量一般小于0.1.另外,有限回波仿真样本也可能会产生较小的波动,但这对于空间相干长度的结果并无影响.上述结果从两个方面说明了利用该算法能够较为准确地获取大气湍流场中激光回波光场的空间相干特性.
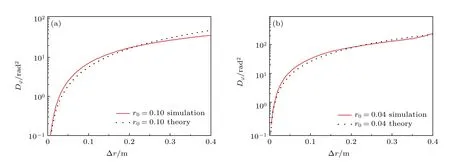
图7 r0不同时,回波光场的PSF 随间距的变化 (a) r0=0.10 m;(b) r0=0.04 mFig.7.PSF of the echo light field at different r0:(a) r0=0.10 m;(b)r0=0.04 m.
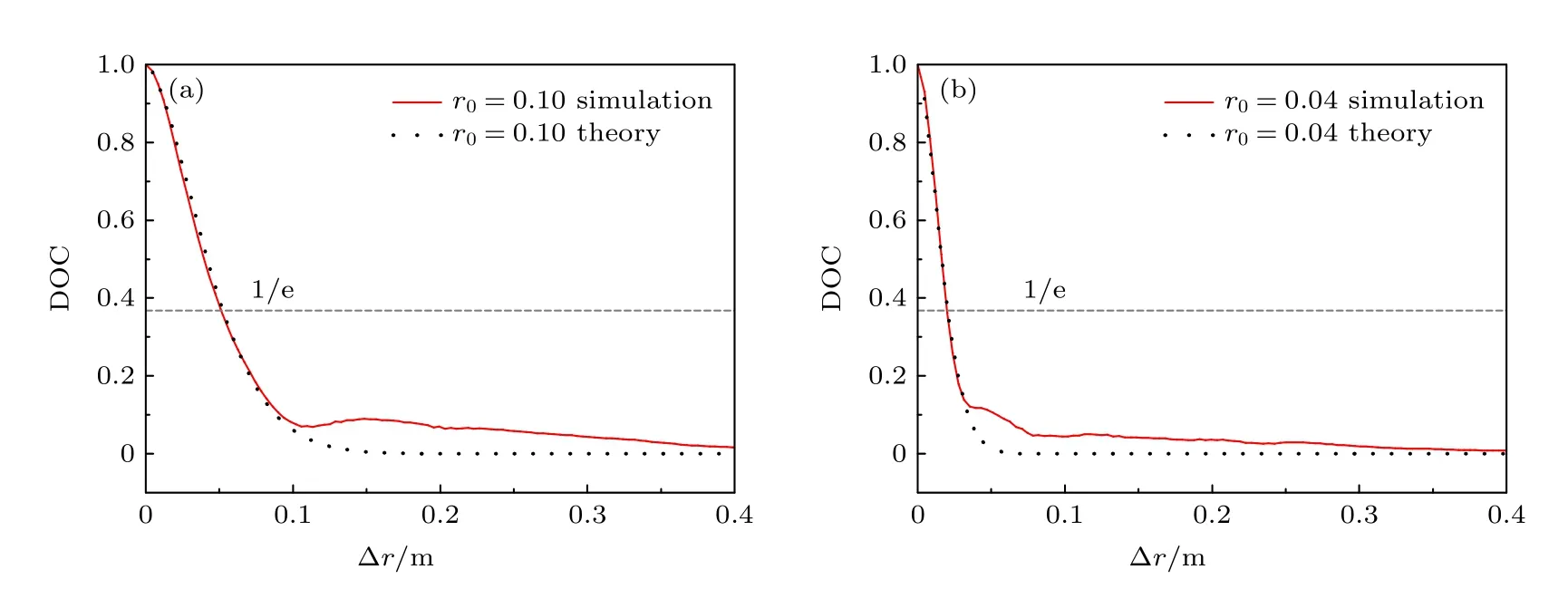
图8 r0不同时,回波光场的DOC 随间距的变化 (a) r0=0.10 m;(b) r0=0.04 mFig.8.DOC of the echo light field at different r0:(a) r0=0.10 m;(b) r0=0.04 m.
4.4 湍流大气中随机粗糙面反射回波的DOC
由PSF 与DOC 之间的关系式D(Δr,zr)=-2 lnµ(Δr,zr)可知,二者可以相互推导,由于DOC相较于PSF 在计算速度、信息容量上的优势(同时包含振幅和相位信息),故下文选择DOC 对回波的相干性进行定量分析.
4.4.1 随机粗糙面对回波光场DOC 的影响
蒙特卡罗法由Lx,Ly和δh三个参数控制二维粗糙面的特性.其中,相关长度Lx,Ly控制粗糙面在x,y方向的横向起伏变化周期,δh控制粗糙面的纵向起伏量.对于理想平面镜,Lx,Ly→∞,δh→0.随着Lx,Ly逐渐减小,δh逐渐增大,表面越显粗糙.由于湍流大气的相干长度为cm/dm 量级,同时考虑到目标靶面处1 m 上256 个网格数对应的空间分辨率约为3.9 mm,设置Lx,Ly=0.0532 m,使仿真程序在Lx×Ly的面积上有不少于100 个网格点以确保面型表达准确.对于更为粗糙的表面,可进一步提升计算网格分辨率.
为综合考虑湍流与粗糙面的影响,选择r0=0.10 m,2L=2200 m 水平方向传输路径.首先研究不同δh对回波光场DOC 的影响,根据DOC下降到e-1对应的间距为空间相干长度计算结果见图9.图9(a1)—(a3)是δh=0.01λ(接近理想镜面),0.1λ(一般加工的镜面)和λ(粗糙表面)时的粗糙面;图9(b1)—(b3)为对应的接收光斑,随着δh的增大,接收光斑呈现斑点状分布;接收光场的DOC 如图9(c1)—(c3)所示,不难发现随间距增大,DOC降低越来越迅速,在粗糙面δh=λ时,DOC 随距离的增加迅速降为零.可见,回波光场的空间相干性对δh非常敏感,当δh接近波长时,相干性严重退化.
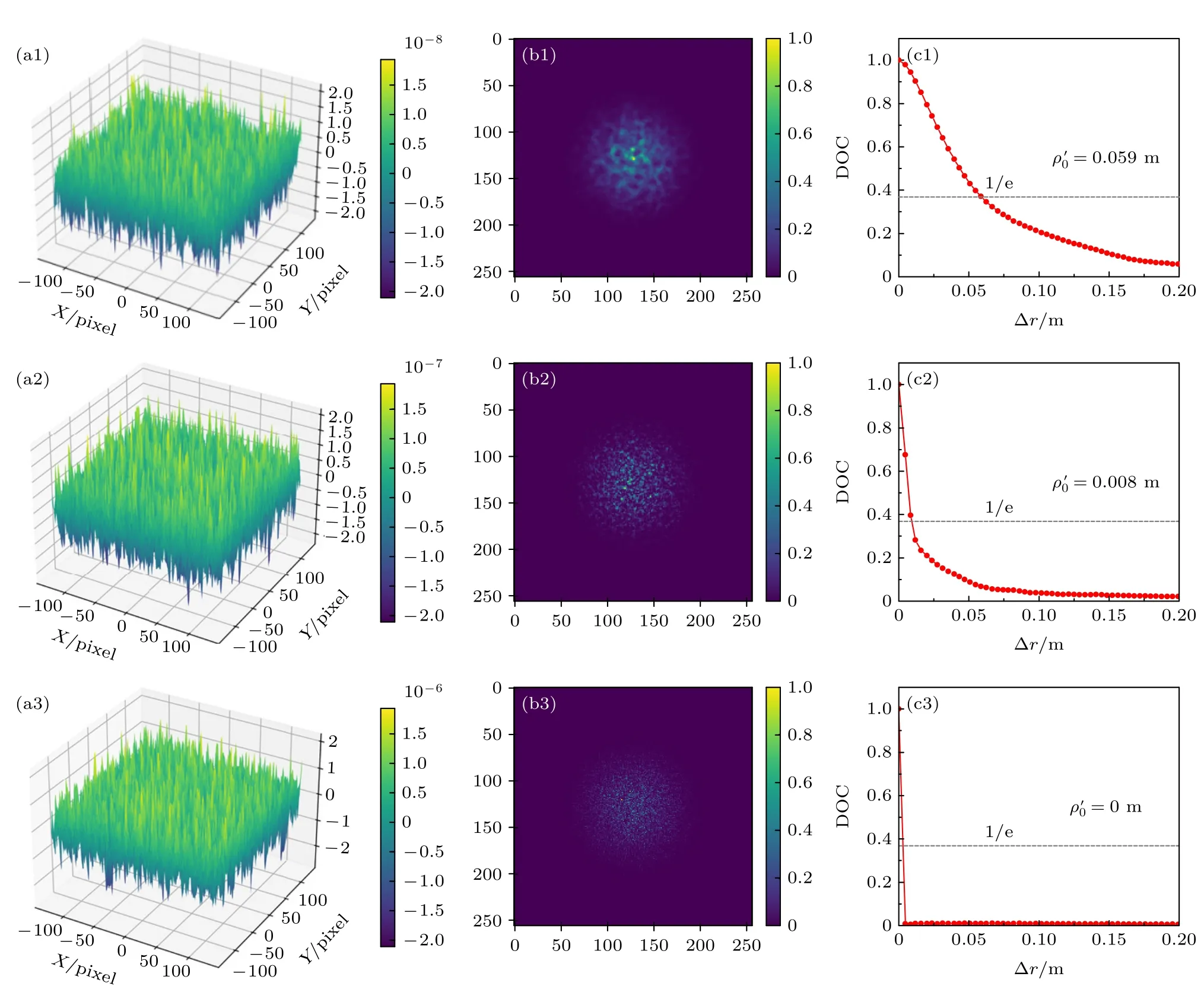
图9 不同δh对应的粗糙反射面、回波接收光强分布及DOC (Lx=0.0532 m) (a1) δh=10-2λ,(a2) δh=10-1λ,(a3) δh=100λ;(b1)—(b3) 对应的回波接收光斑;(c1)—(c3) 对应的回波接收光场的DOCFig.9.(a1)–(a3) Rough reflection surface,echo receiving light intensity and DOC of the receiving light field corresponding to differentδh (Lx=0.0532 m):(a1) δh=10-2λ,(a2) δh=10-1λ,(a3) δh=100λ;(b1)–(b3) the echo receiving light intensity;(c1)–(c3) the DOC of the echo light field.
同样湍流强度条件下,选取δh=10-1λ,镜面受到不均匀应力时,研究不同Lx对应的回波接收光场,计算光场的DOC.仿真结果如图10所示,图10(a1)—(a5)为Lx在0.0266—0.532 m 内的反射面;图10(b1)—(b5)为对应的回波在接收平面处的光强分布,随着目标表面相关长度的减小,光斑从网纹状结构逐渐过渡为细小的散斑颗粒;图10(c1)—(c5)为对应的DOC,其随Lx的减小,衰减越来越快.产生该现象的物理原因是:Lx≫r0时,目标表面对 DOC 的影响较小,仿真结果的空间相干长度(0.0510 m)比较接近设定的空间相干长度ρ0(r0/2.1=0.0476 m) ;当Lx≈r0时,目标表面对DOC 的影响已不可忽视,此时回波光场的相干长度明显小于ρ0;当Lx≪r0时,目标表面对DOC 的影响占据主导,此时回波光场的空间相干性严重退化,已经接近于非相干光,结果与文献[8]实验分析部分相一致.
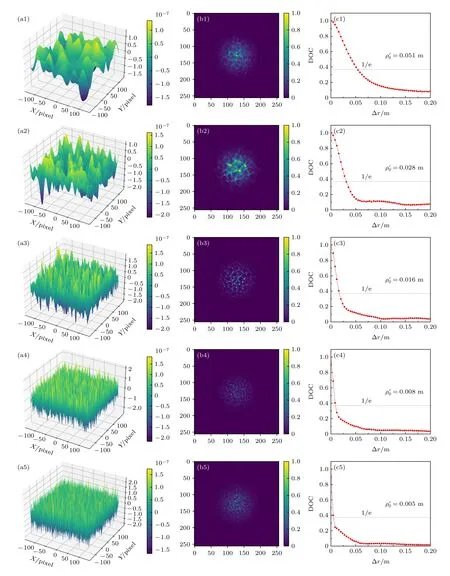
图10 δh=10-1λ,不同Lx对应的粗糙反射面、回波接收光强分布及DOC (a1)Lx=106λ=0.532 m;(a2) Lx=5×105λ=0.266 m;(a3) Lx=2×105λ=0.1064 m;(a4) Lx=105λ=0.0532 m;(a5) Lx=5×104λ=0.0266 m;(b1)—(b5) 对应的回波接收光斑;(c1)—(c5) 对应的回波接收光场的DOCFig.10.Rough reflection surface,echo receiving light intensity and DOC of receiving light field corresponding to differentLxwith δh=10-1λ:(a1) Lx=106λ=0.532 m;(a2) Lx=5×105λ=0.266 m;(a3) Lx=2×105λ=0.1064 m;(a4) Lx=105λ=0.0532 m;(a5) Lx=5×104λ=0.0266 m;(b1)–(b5) corresponding echo receiving light intensity;(c1)–(c5) corresponding DOC of the echo light field.
4.4.2 大气湍流对回波光场DOC 的影响
基于以上研究选择参数为Lx=106λ=0.532 m,δh=10-1λ(平面反射镜或角反射器)的目标反射面来研究大气湍流对回波DOC 的影响.图11(a)为对应的反射面,图11(b1)—(b6)分别为r0=0.02,0.04,0.06,0.08,0.10,0.12 m 时的接收光斑,图11(c)为对应的DOC.可以发现随着r0的增加,DOC 随空间的衰减变慢.产生该现象的物理原因是:当目标反射面较为光滑时,传输路径上的大气湍流对光束带来的扰动成为相干性退化的决定性因素,湍流强度与空间相干长度呈正相关.换言之,此时DOC的变化反映湍流强度的改变,如表2 所列,通过仿真得到大气相干长度与设定参数大气相干长度r0之间的Pearson 相关系数为0.998,这表明由接收光场DOC 计算得出的r0具有良好的可信度,也说明可以通过湍流中传输光束的空间退相干来探测大气湍流的强度信息.
表2 仿真获得的与设定参数r0的对比Tabl e 2.The setting parameters obtained by simulation compared with .
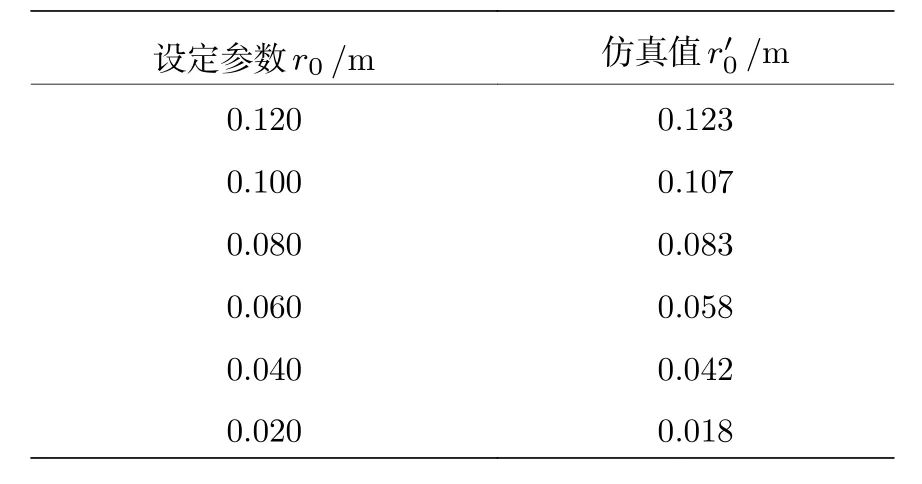
表2 仿真获得的与设定参数r0的对比Tabl e 2.The setting parameters obtained by simulation compared with .
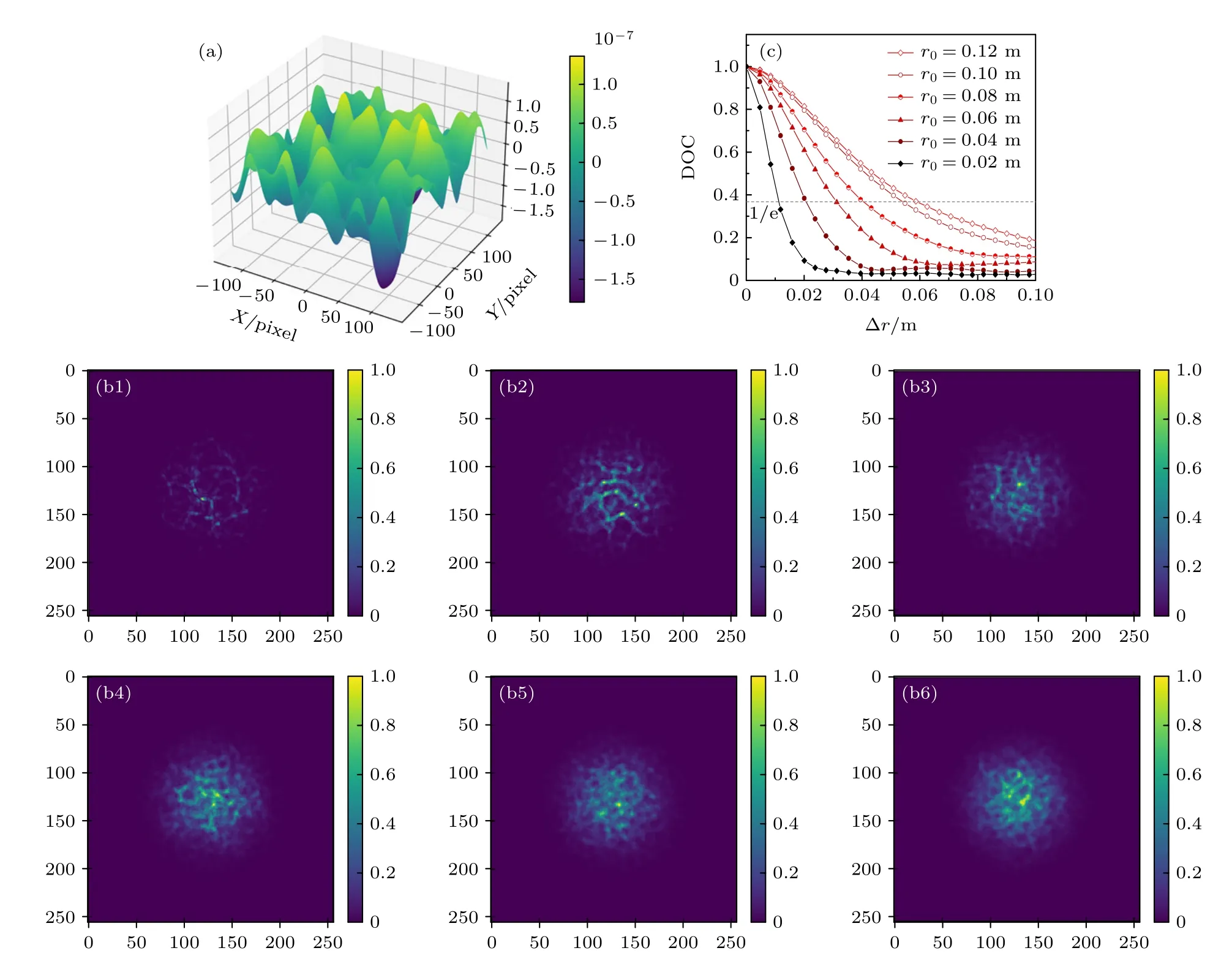
图11 不同湍流强度条件下的回波光场以及对应的DOC 随间距的变化 (a) δh=10-1λ,Lx=106λ时的目标反射面;(b1)—(b6) r0=0.02,0.04,0.06,0.08,0.10,0.12 m 时的接收光斑 ;(c) r0不同时,回波光场的DOCFig.11.The echo light field and corresponding DOC under different turbulence intensity conditions change with the spacing:(a) The target reflection surface under the condition of δh=10-1λ,Lx=106λ;(b1)–(b6) received spot at r0=0.02,0.04,0.06,0.08,0.10,0.12 m;(c) DOC of the echo light field under different r0.
5 结论
本文采用展开式激光往返传输模型,结合湍流相位屏分步传输算法和二维随机粗糙表面的生成模型,实现了von Karman 湍流谱条件下激光回波光场的仿真计算,获得了不同表面粗糙度参数和不同湍流状态下的激光回波强度空间分布特征.并在镜面反射条件下,将激光回波DOC 和PSF 的计算结果与理论值对比,进一步检验了算法的正确性.然后,在1.1 km 的均匀传输路径上,计算了接收平面处激光回波光场在不同空间距离上的DOC值随目标表面高度均方根δh、相关长度Lx和路径上大气湍流强度r0的变化关系.结果表明:DOC随δh的增大而减小,随Lx和r0增大而增大;令r0=0.1 m,当δh增大到光波波长量级或当Lx≪r0时,回波光场的空间相干性严重退化,并趋于非相干光;当δh=10-1λ且Lx≫r0时,目标表面接近镜面,此时通过测量激光回波的空间相干长度来反演传输路径上的大气相干长度具有相当高的可信度;当Lx接近r0时,目标表面δh和大气湍流强度对DOC的影响都不可忽略,需要通过仿真算法来精确计算.下一步,我们将利用该仿真算法,结合已知的目标表面,研究反演路径湍流强度的相干探测方案.
