基于忆阻器阵列的下一代储池计算*

任宽 张握瑜 王菲 郭泽钰 尚大山†

1) (中国科学院微电子研究所,微电子器件与集成技术重点实验室,北京 100029)

2) (西南交通大学超导与新能源研究开发中心,磁浮技术与磁浮列车教育部重点实验室,成都 610031)

3) (中国科学院大学,北京 100049)

储池计算是类脑计算范式的一种,具有结构简单、训练参数少等特点,在时序信号处理、混沌动力学系统预测等方面有着巨大的应用潜力.本文提出了一种基于存内计算范式的储池计算硬件实现方法,利用忆阻器阵列完成非线性向量自回归过程中的矩阵向量乘法操作,有望进一步提升储池计算的能效.通过忆阻器阵列仿真实验,在Lorenz63 时间序列预测任务中验证了该方法的可行性,以及该方法在噪声条件下预测结果的鲁棒性,并探究忆阻器阵列阻值精度对预测结果的影响.这一结果为储池计算的硬件实现提供了一种新的途径.

1 引言

理解生物大脑中信息的加工、处理模式,并在此基础上构建类脑计算硬件系统是现代信息科学的前沿研究之一[1].研究表明,生物大脑等效于一个复杂神经网络动力学系统[2],其处理外界信息的机能依赖于神经网络的动力学过程[3].如何理解大脑的神经动力学过程、构建类脑动力学系统,是类脑计算硬件系统实现的核心问题[4].自然界中的信息大部分是用时序数据来定义的.大脑的动力学系统受外部时序信号刺激,并将刺激产生的数据进行编码和存储[5,6],进而形成各类认知过程.循环神经网络(recurrent neural network,RNN)[7]是一种具有短时记忆能力的神经网络,其中的神经元通过具有环路的网络结构,不仅可以接受其他神经元的信息,也可以接受自身的信息,从而使网络具有处理时序数据的能力,因此,更加适合模拟大脑的动力学系统.当前,RNN 已经被广泛应用于语音识别、自然语言处理等任务中.然而,由于梯度消失和爆炸问题[8],RNN 需要的超参数多,而且训练过程复杂.因此,RNN 在硬件系统实现上依然面临结构复杂、训练时间长和能耗高等问题[9].

储池计算(reservoir computing,RC)是RNN的一种简化形式.RC 概念最初的提出是为了模拟生物大脑中具有大量循环连接的皮质纹状体系统处理视觉空间序列信息的过程[10].随后人们基于RNN 的框架,构建了统一的RC 计算框架[11−13](如图1(a)).RC 的核心是一个被称为“储池”的循环神经网络隐藏层.该网络能够将时序输入信号转换到高维空间中.经过高维转换后,输入信号的特征就可以更容易地通过简单线性回归方法有效读出.目前,RC 在时序信号处理[14]、混沌动力学系统预测[15]等动力学系统学习方面有良好的功能.值得注意的是,与标准RNN 相比[16],RC 中只需要训练输出层权重,并且不需要反向传播算法,有效避免了梯度消失问题,因此,可以有效降低训练复杂度和训练时间.

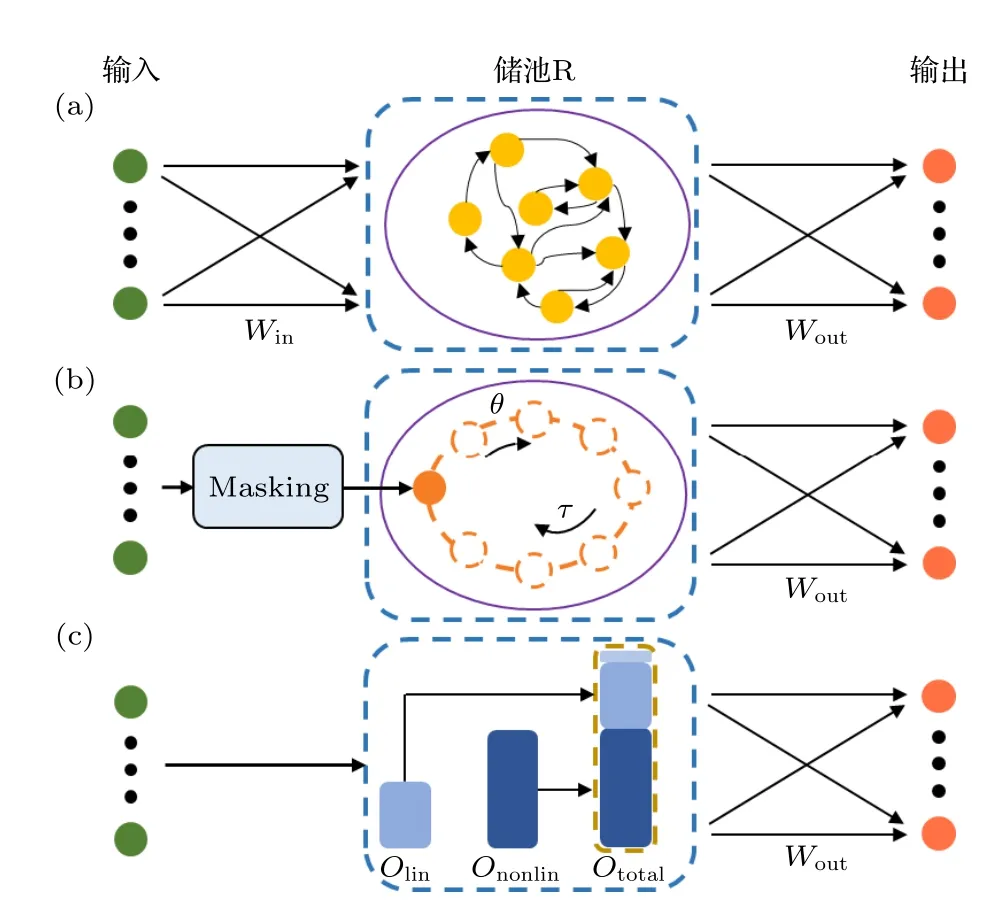
图1 三种RC 结构 (a) 传统RC 结构;(b) 单节点延时RC结构;(c) 非线性向量自回归RC 结构Fig.1.Three types of RC frameworks:(a) Conventional RC;(b) RC using a single nonlinear node reservoir with time-delayed feedback;(c) NGRC,which is equivalent to nonlinear vector autoregression.

传统RC 主要包括由Jaeger[11]提出的ESN 模型（echo state network）和Maass 等[13]提出的LSM（liquid state machine）模型,他们的结构都如图1(a)所示,包含输入、储池和输出三部分.ESN模型的储池和LSM 模型的储池都为基于RNN 框架,由多个神经元随机连接而成的结构.所不同的是,ESN 模型中的神经元是离散时间人工神经元,而LSM 模型中的神经元是具有兴奋性和抑制性的脉冲神经元.储池计算模型结构(以ESN 为例)可以用以下公式描述:

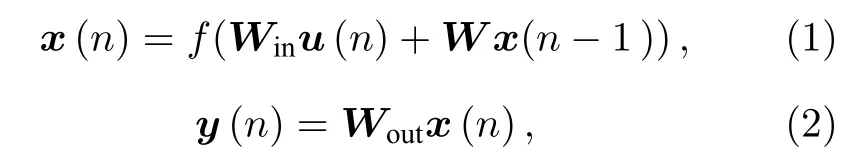
其中,u(n)为输入向量,n为离散的时间,f表示储池层单元的非线性激活函数,Win为输入连接储池的权重矩阵,x(n)是所有离散时间人工神经元的回声状态向量,W为神经元间的连接矩阵,Wout为储池连接输出的权重矩阵,y(n)为输出向量.储池计算只需要训练输出权重矩阵Wout,其性能取决于储池神经元间的连接矩阵W.当W的谱半径小于1 时(即特征值的绝对值的最大项),对任意输入都可以得到对应的回声状态属性[17].节点的回声状态属性等效于节点具备“衰退记忆”[18].人们从理论上证明了,由离散时间“衰退记忆”节点构成的RC 网络在输入有界的情况下具备动力学通用逼近能力[19].

这类RC 的硬件实现方法可大致分为两种:一种方法是通过使用神经网络硬件或神经形态计算技术实现,如用模拟电路[20]、FPGA（fieldprogrammable gate array）[21,22]、大规模集成电路[23]、忆阻器[24−26]等直接构造储池中多个随机连接的神经元.这种方法可灵活调整神经元间连接的拓扑结构以改善性能,但是构造神经元需要的器件众多,并且计算中每一个时间步都需要进行大量计算以及存储大量神经元的状态.另一种方法是采用具备“衰退记忆”的物理节点代替随机连接的神经元,构成储池的动力学系统,如纳米线网络[27,28]、光学器件网络[29]、易失性忆阻器网络[30]等.这种方法利用物理节点的“衰退记忆”特性进行计算.储池的存与算在节点网络中同时进行.然而由随机连接的物理节点构成的动力学系统无法调整节点连接的拓扑结构,故这种方法在面对不同任务时,RC 的性能具有一定的不稳定性.

为了提高RC 的性能,研究人员对RC 结构进行了多种改进(如多储池计算[31]、进化储池计算[32]等),以及将RC 与其他特征提取方法(如卷积神经网络[33]、强化学习[34]、注意力学习[35]等)相结合.目前,传统RC 及其改进方法已经成功地被应用于众多领域,如生物医学、声音识别、无线电等[36].然而,由于储池结构中神经元很多,神经元状态存储以及更新需要大量的硬件资源,并且由于神经元连接拓扑结构难以调整,导致储池计算的参数优化困难.

RC 中神经元节点间相互作用产生的高维信号可以通过延时动力学系统来实现.其状态方程描述为[37]

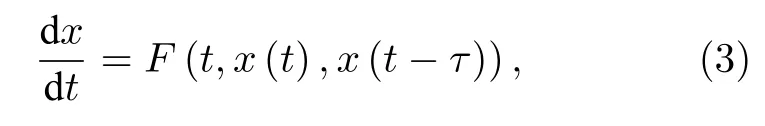
其中,t为连续时间信号,x(t)为系统的状态,F为系统函数,τ为延时时间.2011 年,Appeltant 等[38]提出基于延时动力学系统的单延时节点RC 结构(见图1(b)).输入信号通过掩码函数(masking)进行时间复用,然后输入到单个物理节点在时间维度上展开的虚拟节点中.虚拟节点通过平等分割τ的N个时间点上来设置.两个虚拟节点之间的时间间隔为θ=τ/N.所有虚拟节点x[t-(N-i)θ],i=1,···,N共同作为t时刻节点状态,并通过输出层得到计算结果.

单节点延时RC 的提出,使得RC 的硬件实现变得更加便捷,在一定程度上解决了传统储池硬件实现中,由于神经元数量多而导致的神经元状态存储和更新硬件资源问题.这种单节点延时储池已经在光子器件[39]、FPGAs[40]中得到硬件实现,用于语音识别、图像分类和混沌预测等任务中.我们在前期工作中,利用铁电隧道结(FTJ)中超薄铁电层的退极化效应产生的电流延时特性,实现了单节点延时储池计算功能[41].为了拓展单节点延时RC功能,我们采用了多个单延时节点储池并联的方式,提高了计算的维度,实现了对动态数字序列的识别功能[41].然而,由于虚拟节点是通过时间切分获得,所以其连接拓扑结构是按时间顺序固定的.这意味着这种延时储池同样存在着参数优化困难的问题.

最近,Gauthier 等[42]提出了一种新型RC,称为下一代储池计算(NGRC).NGRC 是一种特殊的非线性向量自回归过程,其等效于具有线性激活节点的储池与一个非线性读出层的结合,如图1(c)所示.NGRC 模型描述为

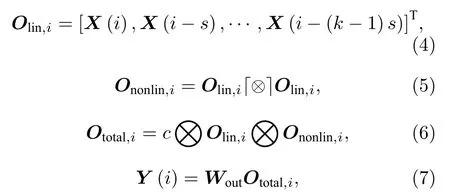
其中,i为离散时间,Olin,i为线性特征向量,X(i)为第i时刻的输入向量,s为时间间隔,k为构成线性特征向量的组数,Ononlin,i为第i时刻非线性特征向量,功能为将符号两边项进行外积、并收集外积结果的唯一单项式的运算符号,Ototal,i为第i时刻总特征向量,c为常数修正项,Y (i)为输出值,Wout为储池连接输出的权重矩阵.NGRC 目前被证实在完成短期动态预测、长期混沌预测、推断动力学系统不可见数据等三个方面有很好的性能.相对于传统RC 和延时RC,NGRC 使用更小的数据集进行训练,并避免了RC 的参数优化困难问题.然而,非线性向量自回归过程本身仍需要大量硬件计算资源用于乘法计算操作.

忆阻器是近年广受关注的一种具有记忆功能的器件[43].由忆阻器器件构成的交叉阵列[44],可以通过欧姆定律和基尔霍夫定律,以存内计算的方式原位、并行、物理地完成矩阵向量乘运算,有效减少了计算过程中数据的搬运,从而具有功耗低、速度快的优点[45−47].本文将NGRC 过程通过矩阵向量乘法操作简化,提出了一种NGRC 的存内计算硬件实现方法,并利用忆阻器阵列完成矩阵向量乘法操作.通过进行忆阻器阵列仿真完成了Lorenz63时间序列预测任务,验证了该方法的可行性,并研究了忆阻器件电阻精度和波动性对NGRC 预测精度的影响.这一结果为高能效RC 提供了一种新的途径.

2 NGRC 的存内实现方法

传统RC 过程中,每一个时间步都需要更新大量具有“衰退记忆”特性的神经元的状态,然而具有“衰退记忆”特性的线性神经元组成的储池与二次非线性读出层组合,在数学上等效于一种特殊的非线性向量自回归过程.NGRC 是对这种特殊的非线性向量自回归过程的优化[42].NGRC 过程与传统储池计算过程的相同点在于都只需要训练输出权重,但是在输入数据的选择和将输入数据进行高维空间非线性转换的方式上有所不同.

输入数据方面,传统储池输入数据一般为当前时刻的数据,而NGRC 的输入数据中,除了当前时刻的数据,还包括之前时刻所对应的数据.高维空间非线性转换方式方面,传统储池的高维空间非线性转换通过储池中具备“衰退记忆”神经元的非线性激活函数达成.NGRC 结构储池的高维空间非线性转换可分为3 个过程(见图1(c)):1) 选择不同时刻输入数据构成线性特征向量Olin;2)由线性特征向量构造非线性特征向量Ononlin;3) 由线性特征向量与非线性特征向量构造总特征向量Ototal.3 个过程中,线性特征Olin向量是由选择的输入数据直接拼接而成;总特征向量Ototal是由固定常数c、线性特征向量Olin与非线性特征向量Ononlin直接拼接而成;而由线性特征向量Olin构造非线性特征向量Ononlin则需要经过一个非线性转换过程.NGRC中的非线性转换过程将线性特征向量Olin通过外积操作映射到一个高维空间中,并在高维空间中去除对应映射向量的重复部分,得到非线性特征向量Ononlin.

NGRC 的非线性转换过程虽然避免了传统储池中随机连接的性能不确定性与需要同时更新多个神经元状态的复杂性,但其向量间的外积操作与除去高维向量重复部分的操作仍然需要大量硬件开销与时间开销.我们注意到相同向量间的外积可以用矩阵向量乘法(matrix vector multiplication,MVM)来表示,去除重复映射向量的操作可以通过保留外积后固定位置元素的值(保留元素操作)来实现.硬件上,使用忆阻器阵列进行MVM 操作,使用忆阻器阵列的选择线电路进行保留元素操作.

2.1 线性特征向量的构建

图2(a)为三维空间时序数据预测任务的NGRC储池的存内实现结构.其中,ti=i×Δt,Δt为采样间隔,i为离散时间数,s为时间间隔数,x(t),y(t),z(t)分别表示预测点在t时刻的x轴、y轴、z轴三维空间坐标,k为每个线性特征向量所取数据的组数.当已知ti时刻及之前时刻点的轨迹坐标,要预测ti+1时刻点的坐标时,取k=2,即令ti时刻和ti-s时刻空间点的三维坐标构建第i个线性特征向量Olin,i,有

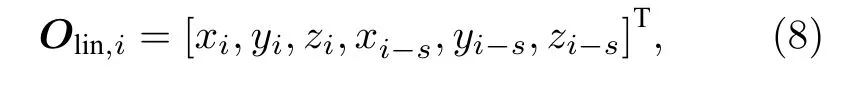
其中,[xi,yi,zi]与[xi-s,yi-s,zi-s]为ti时刻与ti-s时刻点的三维坐标.将构建的线性特征向量Olin,i用时序电压脉冲幅值编码和电导编码,编码的电压序列矩阵Vlin,i为

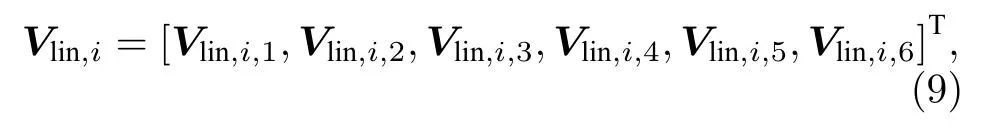
其中列向量Vlin,i,a的第a行的值,为线性特征向量Olin,i中第a个元素对应的量化电压值,列向量中的其他值为零.线性特征向量Olin,i编码的电导矩阵为

其中,Glin,i,a为Olin,i中的第a个元素对应的量化电导值.将电导序列使用差分编码存储到忆阻器阵列中;再将电压序列Vlin,i通过Bitline 输入到忆阻阵列中,具体过程如图2(b)所示.需要指出的是,电压脉冲幅值编码需要经过一个数模转换器(DAC).DAC 的精度与忆阻器本身的精度影响着整体精度.

2.2 非线性特征向量的构建

构建非线性特征向量需要对线性特征向量进行外积操作与保留元素操作.忆阻器阵列中,每通过一个电压序列向量Vlin,i,a,能从阵列输出端(SL)得到一个电流向量Ilin,i,a,总电流矩阵由欧姆定律和基尔霍夫定律可表达为

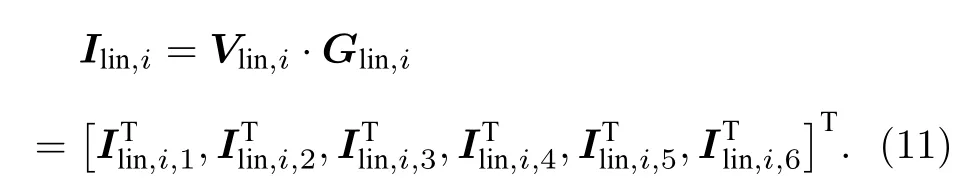
保留Ilin,i矩阵中的非零元素,Ilin,i,a保留元素操作后的向量为Ilin,i,ap,保留元素操作可通过只读取忆阻器阵列电流输出中对应位置的输出实现,过程如图2(a)中绿框部分所示,将选择读取的输出电流组成非线性特征向量Ononlin,i,可表达为

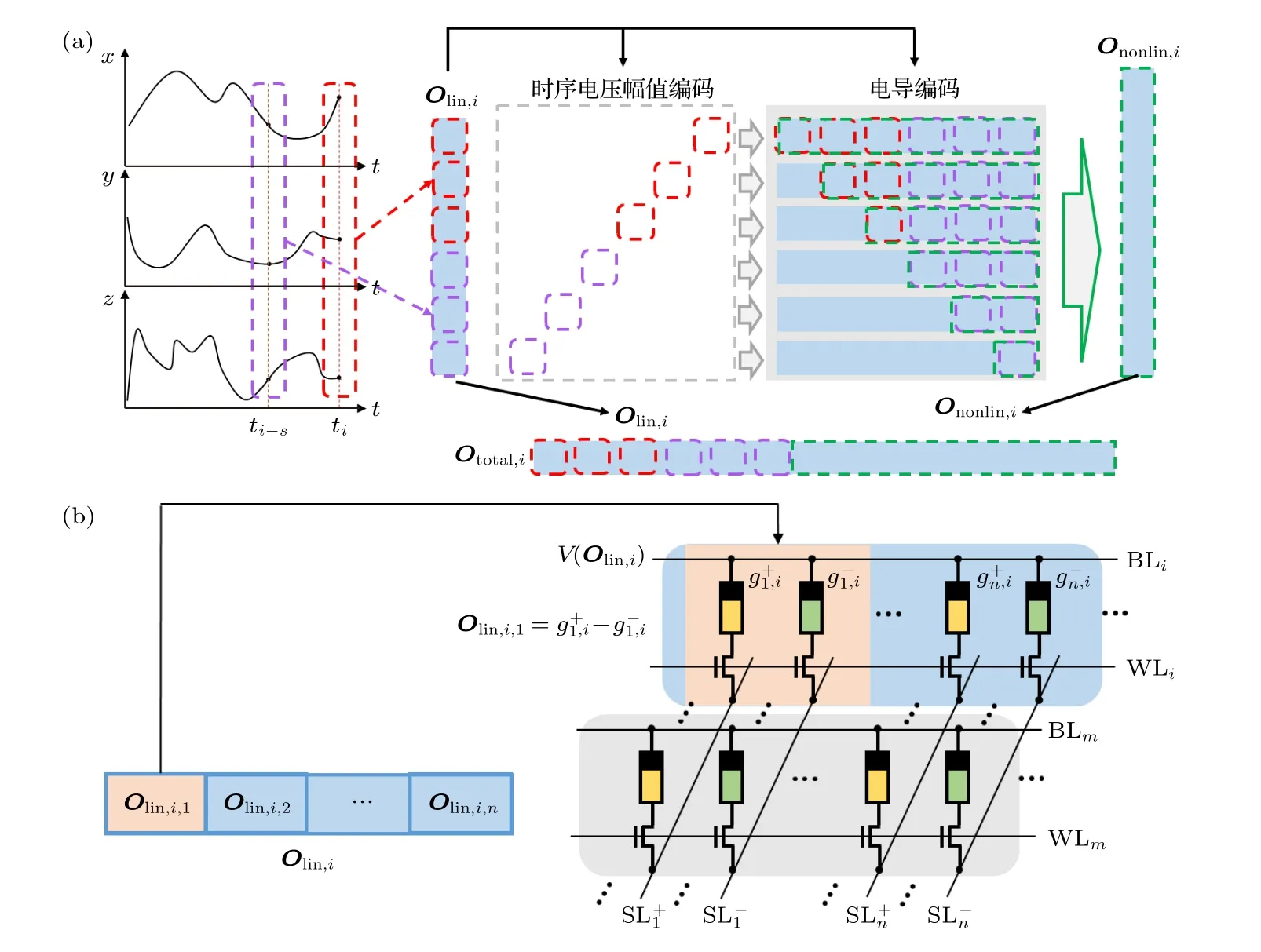
图2 基于忆阻阵列的NGRC 储池结构 (a)用于预测三维时序信号的NGRC 储池结构.输入为三维时序信号;提取ti 时刻(红色框)和ti-s(紫色框)时刻信号的值组成线性特征向量Olin,将第i 个线性特征向量编码为时序电压和电导,时序电压作为忆阻器阵列的输入,电导映射到忆阻器阵列上作为权重;非线性特征向量Ononlin由忆阻器阵列特定单元(绿色方框)的输出构成;总特征向量由Olin与Ononlin直接拼接而成.(b) 图(a)中的线性特征向量Olin,i映射到忆阻器阵列的方式.Olin,i中的每一个值都由两个忆阻器电导的差分g+,g–表示Fig.2.Structure of the NGRC based on memristor-based crossbar.(a) Structure of the NGRC reservoir for three dimensional (3D)timing signals predicting.The input is a 3D timing signal.The linear feature vector Olin is formed by extracting the signal values of ti time (red box) and ti-s time (purple box).The ith linear feature vector is encoded as timing voltage and conductance,and the timing voltage is the input of the memristor array,and the conductance is mapped to the memristor array as weight.The nonlinear feature vector Ononlin consists of the outputs of specific elements of the memristor array (green boxes).The total feature vector is directly spliced by Olin and Ononlin.(b) The way the linear feature vector Olin, i in panel (a) mapping to the memristor array.The g+and g– represent the device conductance values for the positive and negative weights in the differential pair,respectively.

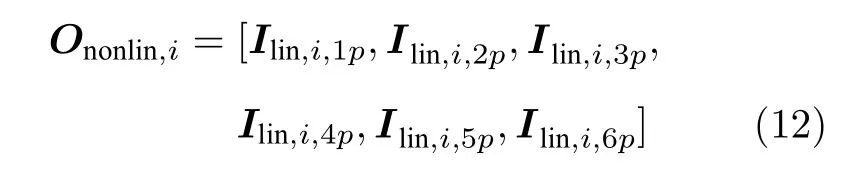
2.3 总特征向量的构建及输出

ti时刻的总特征向量Ototal,i是由固定常数c、线性特征向量Olin,i与非线性特征向量Ononlin,i直接拼接而成,表示为

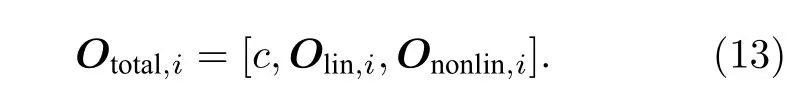
ti+1时刻点的预测位置可直接由总特征向量乘以输出权重得出:

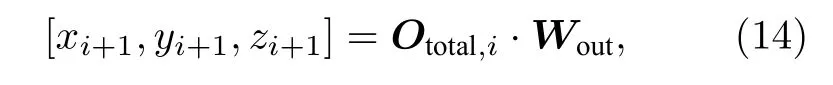
其中,[xi+1,yi+1,zi+1]为所预测的ti+1时刻点的三维坐标,Wout为预先用岭回归方法训练好的输出权重矩阵.值得注意的是,忆阻器电流值的读出需要一个模数转换器(ADC),ADC 的精度也会对最终预测精度造成一定影响.

2.4 训练过程

储池训练过程只训练输出层Wout,训练采用岭回归方法,先用训练数据集得到由特征向量组成的特征矩阵Ototal,以及所有特征向量对应的输出组成的结果矩阵Yd,岭回归方法表达为

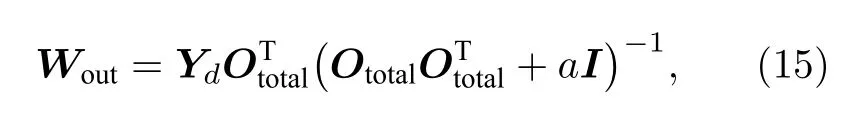
2.5 仿真平台

仿真平台基于python 3.8,pytorch1.9.1(主机GPU 型号NVIDIA GeForce RTX 3080,CPU 型号i9-11980HK)构建,其结构示意图如图3 所示,可分为输入部分、权重部分和输出部分.

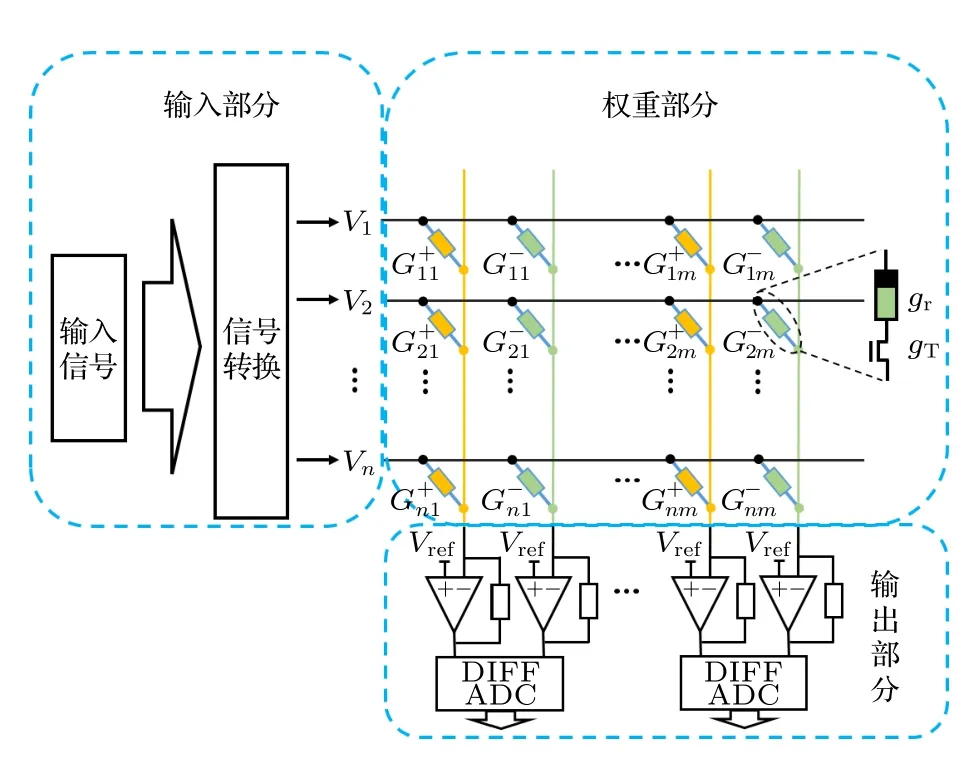
图3 基于忆阻器阵列(包括正、负列)的矩阵乘法运算仿真平台结构示意图,gr 为忆阻器的电导,gT 为晶体管电导Fig.3.Simulation platform of memristor array (including positive and negative arrays) as analog dot-product engine.The memristor conductance corresponds to gr and the transistor conductance corresponds to gT.

输入部分模拟将外界信号转换为电压信号的过程,最高转换精度为定点32 bit.权重部分模拟将外界信号映射到忆阻器阵列中(将带符号的权重映射到一对忆阻器差分电导上)并进行运算的过程,量化电导映射公式为

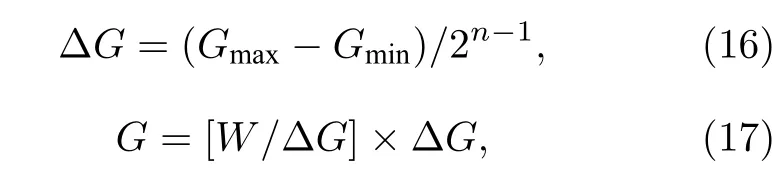
其中n为权重精度(单位 bit),Gmax和Gmin为忆阻器可变化的最大电导与最小电导,[x]为取整操作,W为需要映射的权重,G为映射到忆阻器阵列对应位置的电导值.输出部分模拟忆阻器阵列输出经过ADC 转变为电脑可处理数据的过程,输出精度为所使用ADC 的精度.

3 实验结果与讨论

动力学系统的短期预测能力与动力学系统的长期预测能力通常被用来作为衡量RC 性能的基准,我们将用经典混沌动力学系统模型-Lorenz63模型的短期预测任务与长期预测任务,验证基于忆阻器阵列实现的NGRC 结构的可行性及其对噪声的鲁棒性.Lorenz63 是1963 年洛伦兹[48]提出来的天气预测模型,由3 个方程组成:

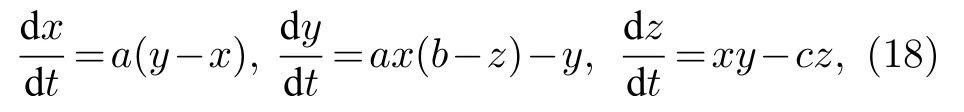
其中状态X(t) ≡ [x,y,z]T是一个分量为Rayleigh-Bénard 的对流可观测量的矢量,a=10,b=28,c=8/3.Lorenz63 模型确定性的混沌行为体现在其对初始条件的敏感依赖(蝴蝶效应),以及在相空间轨迹形成奇异吸引子(图3).

动态系统的预测任务中,用原序列(由动态系统方程得到的序列)与预测序列(储池不断将此时刻输出值作为下一时刻的输入值进行预测得到的序列)之间的结构相似度来衡量预测效果.就Lorenz63 时间序列预测任务而言,归一化均方根误差(NRMSE)可在一定程度上衡量短预测期内的结构相似度,但难以反映长期预测的结构相似度.Lorenz63 时间序列预测的z回归图能直观地反映z变量的长期行为,比较原序列与预测序列的z回归图可以定性地比较两个序列长时段的结构相似度.在之后的Lorenz63 时间序列预测任务中,NRMSE衡量短期预测(1 个李雅普诺夫周期)的结构相似度,通过比较量原序列与预测序列的z回归图衡量长期预测的结构相似度.

在基于忆阻器阵列实现的NGRC 结构的可行性验证实验中,维持系统的输入精度不变,通过改变系统的权重精度(忆阻阵列中忆阻器的量化映射比特数)和输出精度(忆阻器阵列输出ADC 比特数),研究不同权重精度和输出精度对预测结果的结构相似度的影响.在基于忆阻器阵列实现的NGRC结构对噪声的鲁棒性验证实验中,维持输入精度和输出精度不变,研究不同权重精度以及不同噪声大小对预测结果的结构相似度的影响.

3.1 可行性验证实验

保持输入精度为定点32 bit,输出精度为定点64 bit,在权重精度为4,6,8,16,32 和64 bit 情况下进行预测实验.800 个时间步的预测结果及其xz截面图如图4 所示.可以看出,权重精度在4 和6 bit 时无法产生混沌现象(无洛伦兹吸引子);当权重精度达到8 bit 及以上时,开始产生明显的洛伦兹混沌吸引子.这一结果意味着权重精度对混沌的产生有重要影响.当忆阻器阵列对应的权重精度达到一定值时,基于忆阻器阵列实现的NGRC 结构构成的系统能由稳定状态过渡到混沌状态.

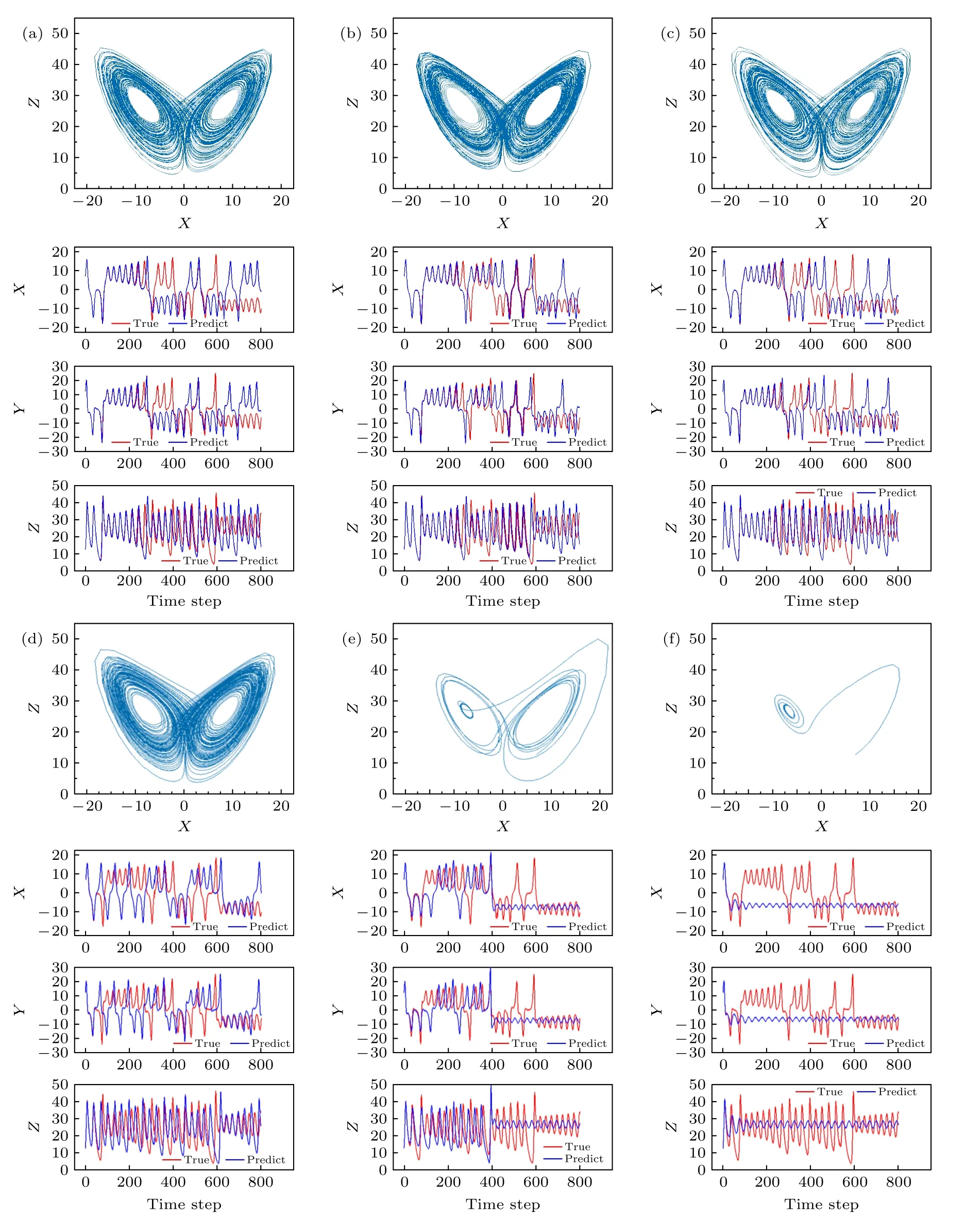
图4 输入精度为定点32 bit,输出精度为定点64 bit,不同权重精度下800 个时间步的预测XZ 截面图 (a) 64 bit;(b) 32 bit;(c) 16 bit;(d) 8 bit;(e) 6 bit;(f) 4 bitFig.4.The XZ cross sections of 800 time steps with different weight precision,when input precision of integer is 32 bit and output precision of integer is 64 bit:(a) 64 bit;(b) 32 bit;(c) 16 bit;(d) 8 bit;(e) 6 bit;(f) 4 bit.

保持输入精度为定点32 bit,通过改变权重精度以及输出精度,在达到混沌状态的前提下探究短期预测结构相似度与权重精度的关系.图5 为短期预测(1 个李雅普诺夫周期)的NRMSE 随不同权重精度(8,16,32,64 bit)和不同输出精度(8,16,32,64 bit)的变化.结果显示,当基于忆阻器阵列实现的NGRC 结构构成的系统达到产生混沌所需的权重精度和输出精度时,短期预测的性能随着权重精度、输出精度的增加而增加.在权重精度不变的情况下,当输出精度达到16 bit,输出精度的增加对短期预测结构相似度几乎无影响;在输出精度不变的情况下,短期预测结构相似度随着权重精度的增加而变高(NRMSE 变小),8 bit 权重精度下的NRMSE 低于0.05,16 bit 权重精度下的NRMSE接近于0,当权重精度超过16 bit 时,权重精度的增加对短期预测结构相似度几乎无影响.

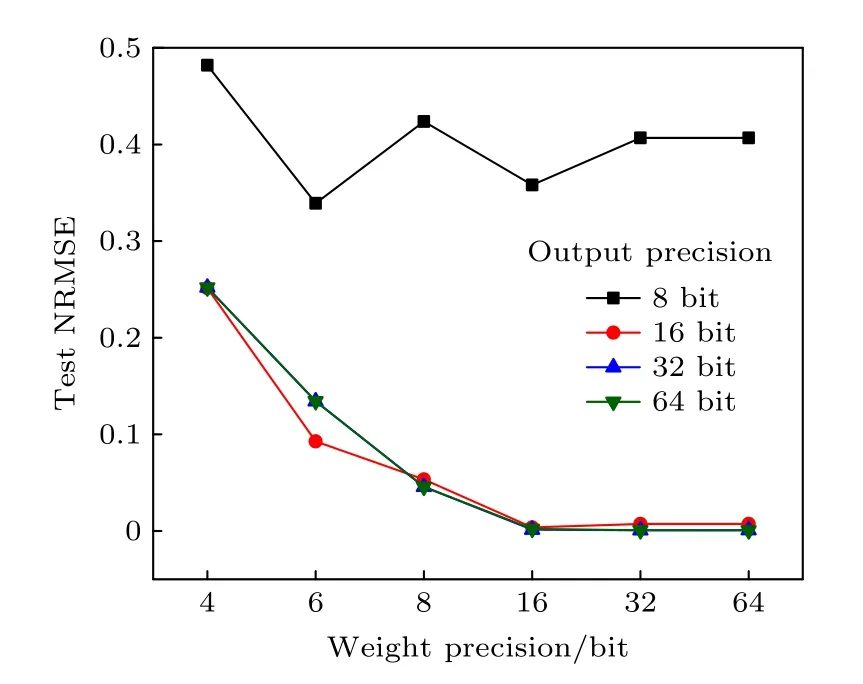
图5 短期预测(1 个李雅普诺夫周期)的NRMSE 随不同权重精度(8,16,32,64 bit)和不同输出精度(8,16,32,64 bit)的变化Fig.5.The variation diagram of NRMSE for short-term prediction (1 Lyapunov cycle) with different weight precision (8,16,32,64 bit) and different output precision (8,16,32,64 bit).

Lorenz63 系统的z分量在连续的局部极大值之间具有函数关系,通过找到z分量的连续局部极大值Mi并根据Mi+1画出Mi形成z回归图,可以简洁地展现z变量的长期行为.Lorenz63 系统的z回归图如图6 所示,紫色点为真实序列z回归图,其他颜色为输入精度为定点32 bit,输出精度为定点64 bit,权重精度分别为8,16,32,64 bit 的z回归图.结果显示,权重精度为8 bit 时的z回归图相比真实序列的回归图有明显偏移;当权重精度在16 bit 及以上时,预测的回归图几乎完全覆盖了真实序列的回归图;随着权重精度的增加,预测的回归图往真实序列的回归图收敛.

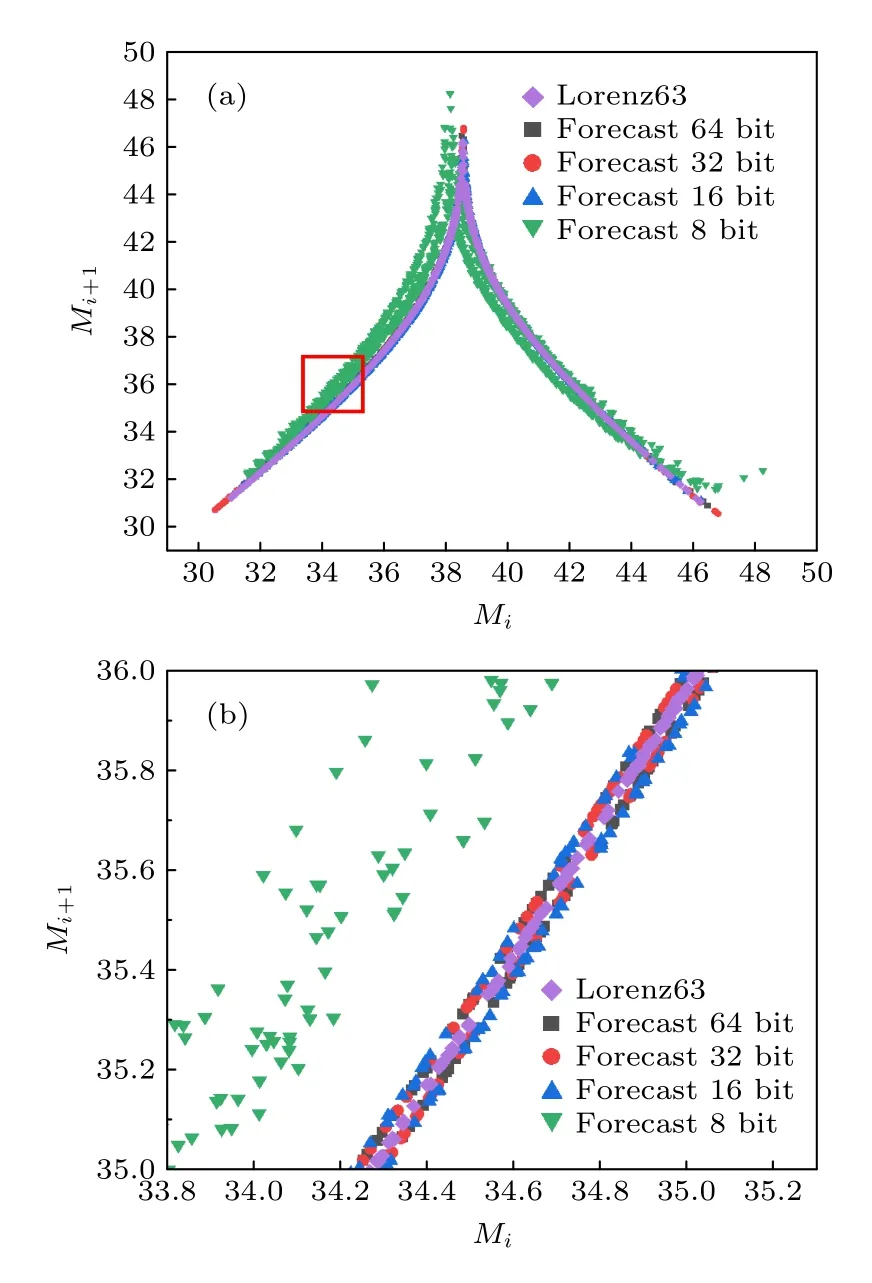
图6 (a) Lorenz63 的z 回归图(紫色)与不同权重精度下预测的z 回归图;(b)图(a)红框区域标记中的放大图Fig.6.(a) The z return map of Lorenz63 (purple) overlaid with the z return map under different weight accuracy;(b) detail of the region marked in Fig.(a).

3.2 噪声鲁棒性验证实验

在保持输入精度为定点32 bit,输出精度为定点64 bit,给权重(即忆阻器电导G)添加高斯噪声NoiseN(0,σ),其中σ=G×10-4×percent为方差,percent 表示噪声强度百分比.短期预测结构相似度的NRMSE 随权重噪声强度变化的结果如图7所示.当权重精度在8 bit 时,随着σ的增大,短期预测结构相似度的NRMSE 会先降低后升高;当权重精度在16 bit 时,短期预测结构相似度的NRMSE也会先降低后升高,但降低点对应的噪声强度比权重精度在8 bit 时小;当权重精度在16 bit 以上时,短期预测的NRMSE 会随着percent 的增大而增大.由于量化本身具备一定的抗噪声能力,故权重精度越低,噪声对短期预测结构相似度的NRMSE的影响越小;值得注意的是,一定程度的噪声有利于提升短期预测性能,并且量化的比特数越高,能带来增益的噪声强度越小.

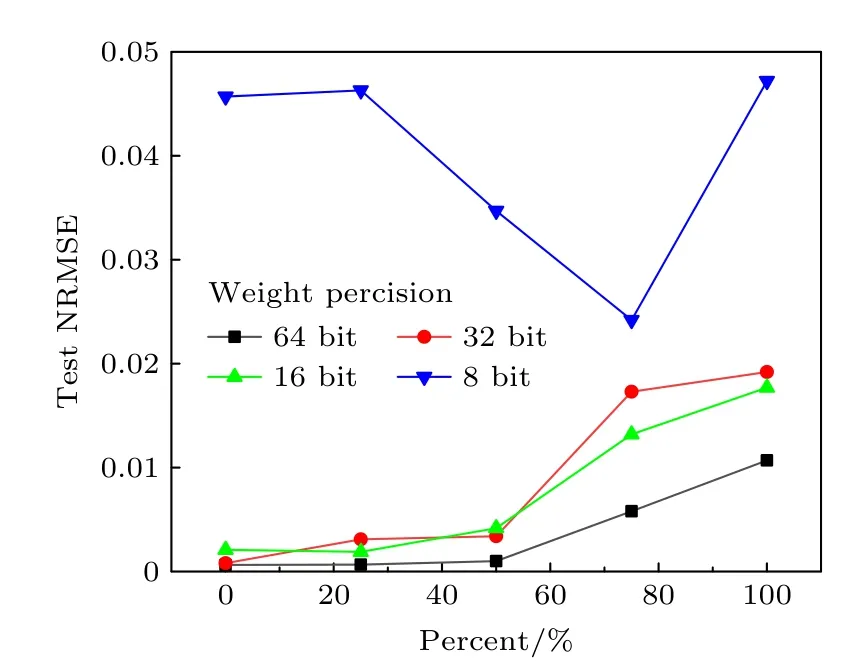
图7 短期预测结构相似度的NRMSE 在不同权重精度条件下随权重噪声强度的变化Fig.7.The variation of NRMSE under different weight precision conditions for short-term prediction with increasing weight noise intensity.

3.3 讨论

基于忆阻器阵列的NGRC 存内实现具备两方面的优势:第一,就NGRC 算法本身而言,相对于传统储池计算和基于延时的储池计算,NGRC 的储池具备更短的激活时间、更少的参数训练量以及更快的训练和推理速度[42];第二,就存内计算方面而言,NGRC 中提取非线性特征向量的过程需要大量的乘法操作,而忆阻器阵列相比传统CMOS电路,在矩阵向量乘法方面具备更快的计算速度和更低的功耗[49].然而,使用忆阻器阵列进行NGRC的过程中,每一次推理过程都需要在忆阻器阵列中写入采样数据;同时,仿真结果表明,忆阻器阵列中每个忆阻器精度达到8 bit,Lorenz63 才能有较好的预测结果.考虑到当前忆阻器还存在各种非理想性因素,因此,如何进一步提高写入效率,同时降低所需忆阻器的阻值精度还需进一步探索.

4 结论

储池计算自提出至今可以分为传统储池计算、延时储池计算和下一代储池计算三个阶段.储池计算性能上的优势不仅来自于算法自身,而且与硬件的实现方式密切相关.本文在总结储池计算发展历程的基础上,提出一种基于存内计算范式的硬件实现方法,将NGRC 过程通过矩阵向量乘法操作简化,并利用忆阻器阵列完成矩阵向量乘法操作.忆阻器阵列仿真实验验证了这一方法在Lorenz63 三维时间序列预测任务中的可行性.仿真实验结果表明,预测效果与输出精度和权重精度密切相关.当输出精度达到16 bit,进一步提高输出精度对预测效果的影响可忽略不计,并且具有良好的抗噪声能力;当权重精度达到8 bit,对Lorenz63 三维时间序列预测的短期预测(1 个李雅普诺夫时间)就可以有良好的预测效果(NRMSE 小于0.05),并可以在一定程度进行长期预测.这些结果为NGRC 的硬件实现提供了一种新的途径,同时也展现了忆阻器阵列在开发基于储池计算的实时、低能耗边缘计算系统方面的潜力.