直线共轭液压泵齿轮齿廓啮合参数的几何分析*
2022-07-25朱学明
朱学明,许 茏
(江苏联合职业技术学院,江苏 盐城 224005)
0 引 言
直线共轭内啮合齿轮泵由于结构紧凑、流量脉动小、噪声低等显著优点在高端机床、塑料机械、海洋装备、航空航天等领域有广泛应用[1]。率先成功研发第一台直线共轭内啮合齿轮泵的是瑞士Turninger公司[2],此项设计技术仍由国外掌握,目前还没有公开完整规范设计体系。
国内大多学者以单一公式法、仿真法研究了直线共轭齿轮泵,而忽略其几何意义。当直线共轭齿轮某些参数超过范围时,纯公式计算将会出现严重错误;同时单一公式计算并不能动态反映动态直线共轭齿轮啮合过程。由于缺乏理论的指导,国内通过仿制法获得的产品仍与发达国家产品有较大差距,研究思路并未获得较大进展,魏伟锋等[3]通过研究指出构建高效啮合几何模型的重要性;徐学忠等[4]研究了直线共轭齿轮,通过向量方程求解速度最终获得滑动系数,过程较为繁琐,同时仅获得单一滑动系数;董永昌等[5]、徐学忠等[6]学者研究了其部分啮合特性,但都缺乏啮合参数的系统分析;许茏等[7]虽然基于Willis定理建立几何模型分析了重合度、啮合线以及共轭线,显示几何分析的巨大威力,但并未对啮合角、压力角、滑动系数啮合参数进行进一步分析和计算。
几何对啮合角、压力角、滑动系数等分析有着先天的优势,若超过范围将无法作图,同时可动态进行分析与计算,因此对其的研究显得非常有必要。专为它开发分析软件并不经济,结合常用的SolidWorks软件、Excel软件就可对直线共轭齿轮啮合的整个过程进行动态分析,从而指导设计。
诸多资料在研究直线共轭内啮合泵时都采用了一些范例,由于这些范例具有通用性,笔者同样以范例形式进行几何分析和计算。重点是通过使用几何方法对直线共轭齿轮的啮合参数进行分析,得出齿廓啮合的规律,为直线共轭齿轮齿廓设计提供参考。
1 工具及基本理论
齿轮设计应考虑各啮合参数如啮合角、压力角、滑动系数等,目前已有资料中的齿轮啮合参数求解都围绕啮合线方程展开。直线共轭齿轮传动是一个动态过程,也是严格的几何啮合过程,同样可通过几何方法进行求解。
1.1 求解工具介绍
SolidWorks是优秀CAD/CAM软件之一,它具有功能强大、易学易用和技术创新的特点,使用它可使设计更加高效。
与本文相关为参数化草图功能,草图中常用的几何关系:水平()、竖直()、垂直(),剪切可自动产生交点()等;一旦标注尺寸,默认为驱动尺寸,也可修改为从动尺寸;参数化草图中数据导入Excel软件后可根据需求设定间隔后进行进一步分析和求解,同时保持几何关系。
1.2 直线齿廓基圆及啮合线概念
直线共轭齿轮组其中一个齿轮齿廓为直线,由于直线特殊性,过圆心O1点作直线齿廓反向延长线的垂线,垂足为F,将以O1F为半径的圆称为直线齿廓齿轮基圆,在传动过程中基圆不发生改变,如图1所示。
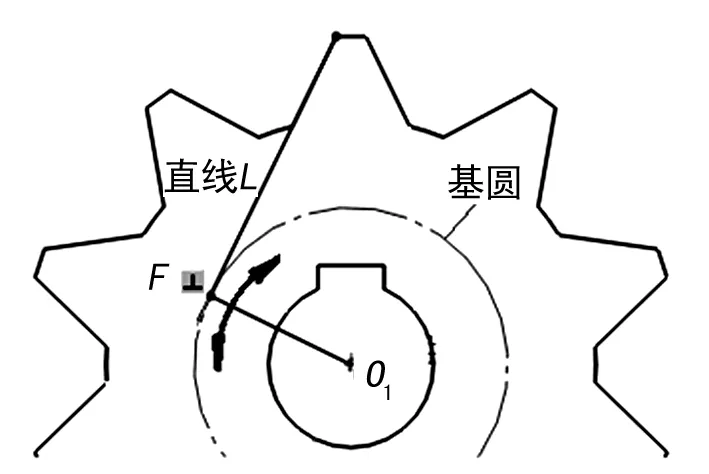
图1 直线齿廓齿轮基圆定义
根据Willis定理[8],过两节圆交点P点作齿轮1直线齿廓所在直线L的垂线,垂足为E点,rj1为节圆1的半径(定值驱动尺寸),O1F为定值(驱动尺寸),拖动直线L(O1F绕着O1旋转,并且保持O1F⊥EF),可获得啮合点E的轨迹即为啮合线,则PE为公法线,直线L(EF)为公切线,如图2所示。
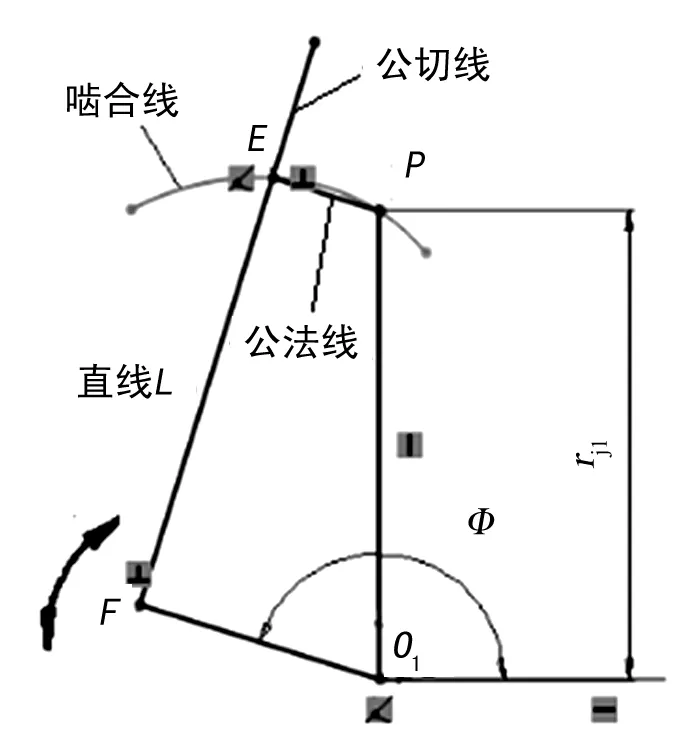
图2 啮合线生成
1.3 啮合角定义
啮合线与两节圆公切线所夹锐角称为啮合角(渐开线齿轮定义)。啮合角较小时,重合度较高,齿面滑动系数较大,齿根较瘦,抗弯强度较差,不适合大扭矩传递,反之相反[8]。
对于直线共轭齿轮,根据定义E点为啮合线上的一点,作两节圆的公切线,则角θ为啮合角,啮合角随着E点的移动而变化。如图3所示,啮合角θ它是一个变化值,和渐开线齿轮啮合角为固定值不同。

图3 啮合角几何定义
1.4 压力角定义
力方向与其作用点速度方向所夹的锐角称为压力角,即该作用点法线方向与速度方向夹角[8]。压力角越小,传动性能好;压力角越大,实际有用功越小,它只增加了摩擦力矩。机构运动中压力角不断变化,一般机构压力角不超过50°。
对于直线共轭齿轮,E点为啮合线上一动点,切线为EF,法线为PE。过E点作EZ垂直于O1E,EZ为速度的方向,如图4所示,角α即为齿轮1压力角,它是一个变化值,同理可几何作图求出齿轮2的压力角。
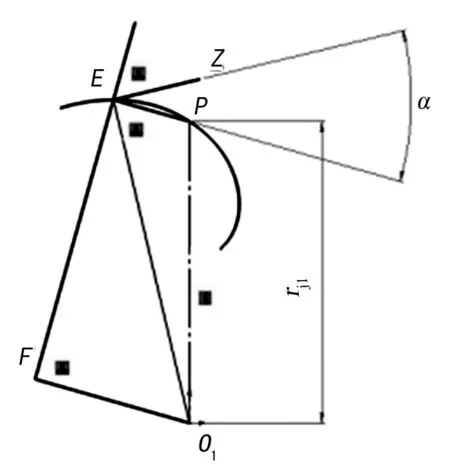
图4 齿轮1压力角几何定义
1.5 滑动系数定义
齿轮啮合点处两齿间相对切向速度(即滑动速度)与该点切向速度的比值称为滑动系数,用η表示[8]。齿轮1的滑动系数为:η1=(vt2-vt1)/vt1;齿轮2的滑动系数为:η2=(vt1-vt2)/vt2。
齿轮啮合传动时,齿廓接触点的相对滑动将会引起齿轮的磨损,而相对滑动的大小又与齿廓曲线的性质有关。齿轮传动一般既有滚动又有滑动,齿轮的齿根滑动系数大于齿顶的滑动系数;小齿轮滑动系数大于大齿轮滑动系数。
2 直线共轭内啮合泵几何分析范例

根据已知条件分析可知内齿轮2节圆半径rj2=34.667 mm、传动比i12=1.3,整体尺寸如图5所示。
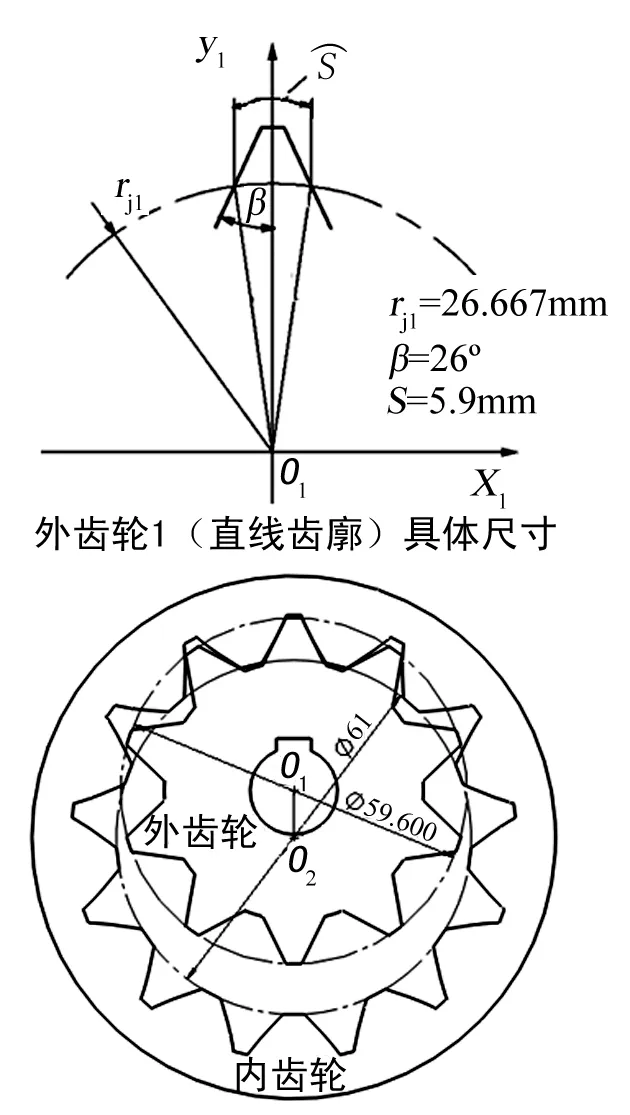
图5 经典直线共轭内啮合齿廓整体尺寸
根据理论分析,外齿轮1齿廓为直线,可作图求解其基圆半径,如图6所示,可知齿轮1基圆半径为O1F=14.264 mm,O1O2=8 mm(图中可省略两尺寸)。
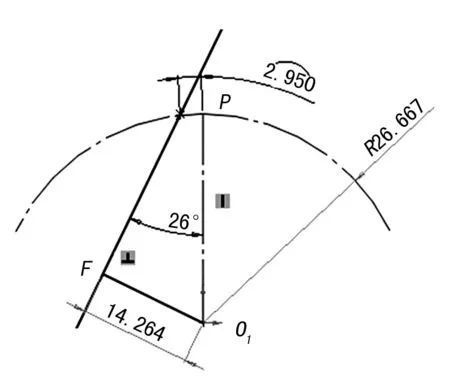
图6 作图求解直线齿轮基圆半径
2.1 啮合角求解过程
(1) 根据1.3节啮合角定义,角θ为啮合角,建立几何模型如图7所示。
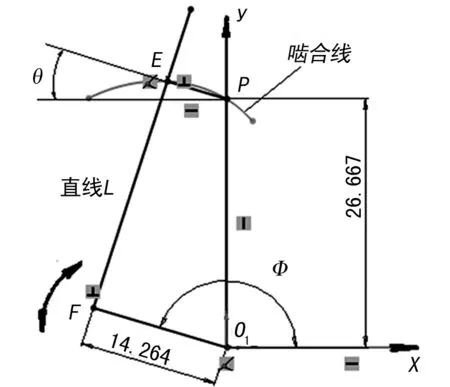
图7 啮合角几何模型
(2) 保持模型几何关系,以啮合点E点的X坐标为驱动尺寸,啮合角θ角为从动尺寸,结合Excel软件,驱动尺寸间隔设置为0.01 mm(以下同),获得关系曲线如图8所示。

图8 啮合角变化分析
(3) 从c点到d点的啮合过程中,啮合角的值逐渐变大,c点啮合角为最小值11.14°(X方向值为-8.94 mm),d点啮合角为最大值48.95°(X方向的值为3.84 mm),啮合角平稳过渡无突变,两极限位置啮合角分析如图9所示。

图9 两极限位置的啮合角
2.2 压力角求解
(1) 根据1.4节定义,如图10所示,角α即为齿轮1的压力角。
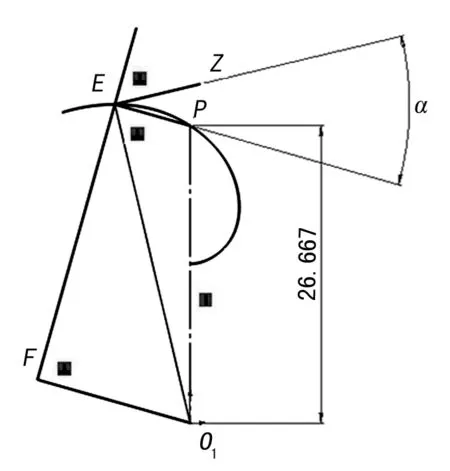
图10 压力角几何模型
(2) 保持模型几何关系,以啮合点E点的X坐标为驱动尺寸,压力角α为从动尺寸,结合Excel软件,关系曲线如图11所示。

图11 直线齿轮1压力角曲线
(3)E点从c点到d点的啮合过程中,齿轮1压力角逐渐变大,c点的压力角为最小值28.60°,d点的压力角为最大值39.17°,压力角的过渡平稳无突变,两极限位置压力角分析如图12所示。
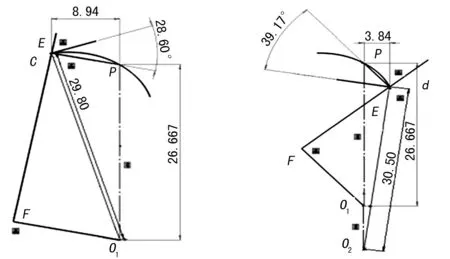
图12 两极限位置的压力角
2.3 滑动系数求解
(1) 根据1.5节定义,过啮合点E点作O1E与O2E的垂线,与直线EF(为啮合的切线)的夹角分别为δ1和δ2,O1E为啮合半径R1,O2E为啮合半径R2,如图13所示。

图13 滑动系数的几何模型
(2) 根据滑动系数的定义,vt1=ω1R1cos(δ1);vt2=ω2R2cos(δ2),ω1为齿轮1转动的角速度;ω2为齿轮2转动的角速度,将传动比关系ω1=1.3ω2代入公式,则η1=(vt2-vt1)/vt1=R2cos(δ2)/[1.3×R1cos(δ1)]-1。根据公式,只要查询啮合E点cd段任一位置的R1、R2、δ1和δ2四个值导入Excel软件,通过公式即可求出滑动系数,滑动系数关系曲线如图14所示。
由于E点公切线方向速度值不同从而引出了滑动系数,在公法线上方向上速度的值应该相同(否则会出现脱离的现象),在Excel中进行计算η法=vt2/vt1=R2sin(δ2)/[1.3×R1sin(δ1)],计算结果皆为1,如图14所示,说明法向的速度相等。

图14 Excel中计算齿轮1滑动和法向系数
(3) 从c点到d点的啮合过程中,滑动系数η1逐渐变大,c点的滑动系数为-0.14 742;两节圆交点处滑动系数为0;d点滑动系数0.094 585,滑动系数的过渡平稳无突变。如图15所示。

图15 齿轮1滑动系数变化曲线
间隔根据需求可在Excel中任意设定,但不能超过其啮合范围,否则它的几何模型无法生成。范例中仅仅求解齿轮1的压力角和滑动系数,同理可求解齿轮2,文中在此不再阐述。
3 结 论
文中重点针对直线共轭液压泵齿轮齿廓啮合参数缺乏统一系统分析的问题,使用了几何方法对其啮合参数进行分析,揭示了内在的动态啮合规律,对直线共轭齿轮齿廓设计有一定参考价值,总结重点如下。
(1) 同样可用参数化草图分析其啮合极限半径等其它啮合参数,文中并没有进一步展开。
(2) 基于Willis定理构建的直线共轭齿轮几何啮合模型简洁准确且高效,根据其几何模型求解啮合参数,比单一公式计算有着先天的优势。
(3) 使用参数化CAD软件省去了繁琐的计算,并且可动态分析整个啮合过程,更适合工程人士使用。
(4) 对直线共轭齿轮啮合参数的研究为进一步研究直线共轭齿轮的流量、功率、阻力等设计奠定了基础。
(5) 所提几何分析方法不但可求解直线共轭齿轮,也可求解其它类型的共轭齿轮。
(6) 通过对直线共轭齿轮啮合几何模型分析可知啮合角、压力角、滑动系数等啮合变化规律,但作为齿轮泵不但要考虑传动特性还需考虑困油、流量等因素。
